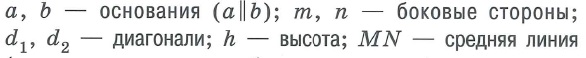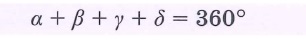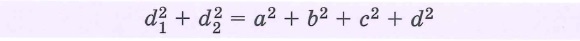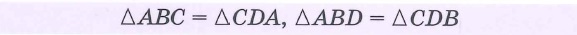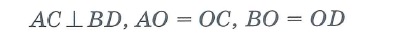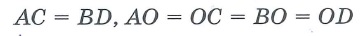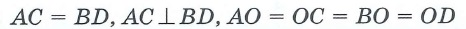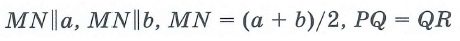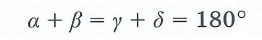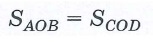Какой четырехугольник называется квадратом перечислите свойства квадрата

Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. Свойства параллелограмма. Свойства ромба. Свойства прямоугольника. Свойства квадрата. Свойства трапеции. Примерно 7-9 класс (13-15 лет)
Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Виды четырехугольников: | |||
|  | ||
|  | ||
|  | ||
|  | ||
|  | ||
Свойства произвольных четырехугольников: | |||
|  | ||
Свойства параллелограмма: | |||
|  | ||
Свойства ромба: | |||
|  | ||
Свойства прямоугольника: | |||
| 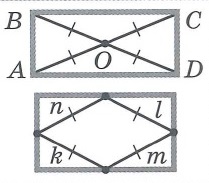 | ||
Свойства квадрата: | |||
|  | ||
Свойства трапеции: | |||
|  | ||
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers
Консультации и техническая
поддержка сайта: Zavarka Team
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
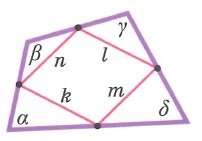
Четырехугольником называется фигура, которая состоит из четырех точек (вершин) и четырех отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.
Четырехугольники бывают выпуклые (ABCD) и невыпуклые (A1B1C1D1).
В задачах ОГЭ встречаются выпуклые четырехугольники, поэтому подробно изучим их.
Смежные стороны – соседние стороны, которые выходят из одной вершины. Пары смежных сторон: AB и AD, AB и BC, BC и CD, CD и AD.
Противолежащие стороны – несмежные стороны (соединяют разные вершины). Пары противолежащих сторон: AB и CD, BC и AD.
Противолежащие вершины – вершины, не являющиеся соседними (лежат друг напротив друга). Пары противолежащих вершин: A и C, B и D.
Диагонали четырехугольника – отрезки, соединяющие противолежащие вершины. AC и BD – диагонали четырехугольника ABCD.
Диагонали выпуклого четырехугольника пересекаются в одной точке.
Площадь произвольного выпуклого четырехугольника можно найти по формуле:
S=12d1d2⋅sinφ
где d1 и d2 – диагонали четырехугольника, φ – угол между диагоналями (острый или тупой – не важно).
Рассмотрим более подробно некоторые виды выпуклых четырехугольников.
Класс параллелограммов: параллелограмм, ромб, прямоугольник, квадрат.
Класс трапеций: произвольная трапеция, прямоугольная трапеция, равнобокая (равнобедренная) трапеция.
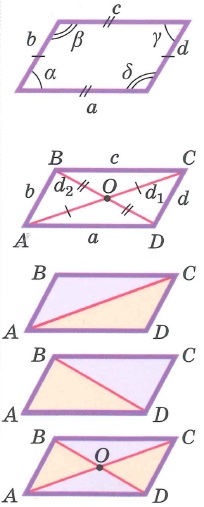
Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.
Свойства параллелограмма:
- Противолежащие стороны равны.
- Противоположные углы равны.
- Диагонали точкой пересечения делятся пополам.
- Сумма углов, прилежащих к одной стороне, равна 180°.
- Сумма квадратов диагоналей равна сумме квадратов сторон. d12+d22=2(a2+b2)
Площадь параллелограмма можно найти по трём формулам.
S=a⋅ha=b⋅hb
Как произведение стороны и высоты, проведенной к ней.
Поскольку стороны имеют разные длины, то высоты, которые к ним проведены, тоже будут иметь разные длины.
S=a⋅b⋅sinα
Как произведение двух смежных (соседних) сторон на синус угла между ними.
S=12⋅d1⋅d2⋅sinφ
Как полупроизведение диагоналей на синус угла между ними.
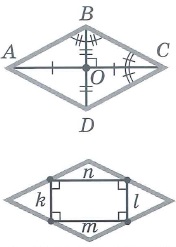
Ромб – параллелограмм, у которого все стороны равны.
Свойства ромба:
- Диагонали пересекаются под прямым углом.
- Диагонали являются биссектрисами углов, из которых выходят.
- Сохраняются все свойства параллелограмма.
Площадь ромба можно найти по трём формулам.
S=a⋅h
Как произведение стороны ромба на высоту ромба.
S=a2⋅sinα
Как квадрат стороны ромба на синус угла между двумя сторонами.
S=12⋅d1⋅d2
Как полупроизведение диагоналей ромба.
Прямоугольник – это параллелограмм, у которого все углы равны 90°.
Свойства прямоугольника:
- Диагонали прямоугольника равны.
- Сохраняются все свойства параллелограмма.
Площадь прямоугольника можно найти по двум формулам:
S=a⋅b
Как произведение двух смежных (соседних) сторон прямоугольника.
S=12⋅d2⋅sinφ
Как полупроизведение диагоналей (так как они обе равны, обозначим их буквой d ) на синус угла между ними.
Квадрат – прямоугольник, у которого все стороны равны.
Свойства квадрата:
- Сохраняет свойства ромба.
- Сохраняет свойства прямоугольника.
Площадь квадрата можно вычислить по двум формулам:
S=a2
Как квадрат стороны.
S=d22
Как полупроизведение квадратов диагоналей (диагонали в квадрате равны).
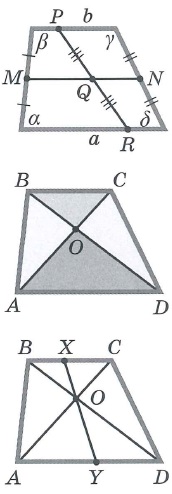
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие нет.
Стороны, которые параллельны друг другу называются основаниями, другие две стороны называются боковыми сторонами.
BC и AD – основания, AB и CD – боковые стороны трапеции ABCD.
Свойства трапеции:
сумма углов, прилежащих к боковой стороне, равна 180°.
∠A+∠B=180°
∠C+∠D=180°
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Средняя линия параллельна основаниям. Её длина находится по формуле: m=a+b2
Площадь трапеции можно найти по двум формулам:
S=a+b2⋅h=m⋅h
Как полусумму оснований на высоту. Поскольку полусумма оснований есть средняя линия трапеции, можно найти площадь трапеции как произведение средней линии на высоту.
S=12d1⋅d2⋅sinφ
Как полупроизведение диагоналей на синус угла между ними.
Виды трапеций
Прямоугольная трапеция – трапеция, у которой два угла прямые.
Равнобокая (равнобедренная) трапеция – трапеция, у которой боковые стороны равны.
Свойство равнобокой трапеции: углы при основании равны
Модуль геометрия: задания, связанные с четырехугольниками
Скачать домашнее задание к уроку 4.
Женя Рудаков · 2 октября 2018
6,7 K
Признаки фигур такие:
- Параллелограмм — это четырехугольник у которого противолежащие стороны параллельны
- Ромб — это параллелограмм, у которого все стороны равны.
- Прямоугольник — это параллелограмм, у которого все углы прямые.
- Квадрат — это прямоугольник, у которого все стороны равны.
- Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие — не параллельны.
Про свойства можно почитать вот тут https://www.dpva.ru/Guide/GuideMathematics/MathsForTheYoungest/PlateFourAngles/
Какие еще есть способы найти площадь треугольника, кроме теоремы Пифагора?
По теореме Пифагора площадь не найти. Теорема Пифагора это теорема о соотношении катетов и гипотенузы в прямоугольном треугольнике.
Формулы площади треугольника.
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
S = 1/2 a · h
2. Формула площади треугольника по трем сторонам. Формула Герона
S = √p(p — a)(p — b)(p — c)
3. Формула площади треугольника по двум сторонам и углу между ними.
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = 1/2 a · b · sin γ
4. Формула площади треугольника по трем сторонам и радиусу описанной окружности
S = a · b · с/4R
5. Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
S = p · r
где S — площадь треугольника,
a, b, c — длины сторон треугольника,
h — высота треугольника,
γ — угол между сторонами a и b,
r — радиус вписанной окружности,
R — радиус описанной окружности,
p = (a + b + c)/2 — полупериметр треугольника.
Для прямоугольного треугольника площадь вычисляется по формуле:
S=a*b/2, где a и b катеты.
Прочитать ещё 2 ответа
Существует квадрат, который не является прямоугольником?
Researcher, Institute of Physics, University of Tartu
Нет. Квадрат (равные стороны), который не прямоугольник, — это уже не квадрат, а ромб. Определение квадрата включает в себя, что у него все углы прямые.
глазки лапки глазки лапки глазки лапки глазки лапки глазки лапки глазки лапки
Докажите что ромб у которого угол между диагональю и стороной равен 45 является квадратом?
подумываю стать крутым программистом, но пока что просто пеку хлебушек
Одно из свойств ромба: его диагонали являются биссектрисами углов. Так как биссектриса делит угол пополам, значит угол между двумя сторонами равен 90 градусам.
В то же время, ромб — это частный случай параллелограмма, а у параллелограмма противоположные углы попарно равны. Значит, противолежащий угол найденому — тоже равен 90 градусам, а так как сумма всех углов равно 360, значит на сумма двух равных неизвестных углов 180.
С помощью несложных вычислений ясно, что они тоже по 90, а значит такой ромб — квадрат 🙂
Прочитать ещё 1 ответ
Какие стороны прямоугольника называют соседними и противолежащими?
Мои интересы: разнообразны, но можно выделить следующие: литература, история…
Соседними называются стороны прямоугольника, которые имеют общий угол и соединяются друг с другом, при этом одна из них вертикальная, а другая горизонтальная. Противолежащие стороны не соединены друг с другом и не имеют общего угла.
По какой формуле можно найти углы параллелограмма?
Родилась в Нижнем Новгороде, волей судьбы оказалась в Москве. Мама двоих детей…
Для того, чтобы найти углы параллелограмма нужно знать хотя бы один из углов. Все 4 угла в сумме 360 градусов. Углы, которые расположены «напротив» друг друга по диагонали — равные. Итого 2х+2у=360,где x и у — углы, прилежащие к одной стороне параллелограмма.
 В школьной программе на уроках геометрии приходится иметь дело с разнообразными видами четырёхугольников: ромбами, параллелограммами, прямоугольниками, трапециями, квадратами. Самыми первыми фигурами для изучения становятся прямоугольник и квадрат.
В школьной программе на уроках геометрии приходится иметь дело с разнообразными видами четырёхугольников: ромбами, параллелограммами, прямоугольниками, трапециями, квадратами. Самыми первыми фигурами для изучения становятся прямоугольник и квадрат.
Итак, что же такое прямоугольник? Определение для 2 класса общеобразовательной школы будет выглядеть так: это четырёхугольник, у которого все четыре угла прямые. Несложно представить себе, как выглядит прямоугольник: это фигура с 4 прямыми углами и сторонами, попарно параллельными друг другу.
Признаки и свойства прямоугольника
Как понять, решая очередную геометрическую задачу, с каким именно четырёхугольником мы имеем дело? Существуют три основных признака, по которым можно безошибочно определить, что речь идёт именно о прямоугольнике. Назовём их:
- фигура является четырёхугольником, три угла которого равны 90°,
- представленный четырёхугольник — это параллелограмм с равными диагоналями,
- параллелограмм, который имеет по крайней мере один прямой угол.
Интересно знать: что такое выпуклый четырехугольник, его особенности и признаки.
Поскольку прямоугольник — это параллелограмм (т. е. четырёхугольник с попарно параллельными противоположными сторонами), то для него будут выполняться все его свойства и признаки.
Формулы для вычисления длины сторон
В прямоугольнике противолежащие стороны равны и взаимно параллельны. Более длинную сторону принято называть длиной (обозначается a), более короткую — шириной (обозначается b). В прямоугольнике на изображении длинами являются стороны AB и CD, а шириной — AC и B. D. Также они перпендикулярны к основаниям (т. е. являются высотами).
Это интересно: в геометрии луч это что такое, основное понятие.
Для нахождения сторон можно воспользоваться формулами, указанными ниже. В них приняты условные обозначения: a — длина прямоугольника, b — его ширина, d — диагональ (отрезок, соединяющий вершины двух углов, лежащих друг напротив друга), S — площадь фигуры, P — периметр, α угол между диагональю и длиной, β острый угол, который образован обеими диагоналями. Способы нахождения длин сторон:
- С использованием диагонали и известной стороны: a = √(d ² b ²), b = √(d ² a ²).
- По площади фигуры и одной из её сторон: a = S / b, b = S / a.
- При помощи периметра и известной стороны: a = (P — 2 b) / 2, b = (P — 2 a) / 2.
- Через диагональ и угол между ней и длиной: a = d sinα, b = d cosα.
- Через диагональ и угол β: a = d sin 0,5 β, b = d cos 0,5 β.
Это интересно: как сравнить два отрезка способы с примерами.
Периметр и площадь
 Периметром четырёхугольника называют сумму длин всех его сторон. Чтобы вычислить периметр, могут использоваться следующие формулы:
Периметром четырёхугольника называют сумму длин всех его сторон. Чтобы вычислить периметр, могут использоваться следующие формулы:
- Через обе стороны: P = 2 (a + b).
- Через площадь и одну из сторон: P = (2S + 2a ²) / a, P = (2S + 2b ²) / b.
Площадь — это пространство, ограниченное периметром. Три основных способа для расчёта площади:
- Через длины обеих сторон: S = a*b.
- При помощи периметра и какой-либо одной известной стороны: S = (Pa — 2 a ²) / 2, S = (Pb — 2 b ²) / 2.
- По диагонали и углу β: S = 0,5 d ² sinβ.
Диагонали прямоугольника
В задачах школьного курса математики часто требуется хорошо владеть свойствами диагоналей прямоугольника. Перечислим основные из них:
- Диагонали равны друг другу и делятся на два равных отрезка в точке их пересечения.
- Диагональ определяется как корень суммы обеих сторон, возведённых в квадрат (следует из теоремы Пифагора).
- Диагональ разделяет прямоугольник на два треугольника с прямым углом.
- Точка пересечения совпадает с центром описанной окружности, а сами диагонали — с её диаметром.
Это интересно: как обозначается площадь, примеры для вычисления.
Применяются следующие формулы для расчёта длины диагонали:
- С использованием длины и ширины фигуры: d = √(a ² + b ²).
- С использованием радиуса окружности, описанной вокруг четырёхугольника: d = 2 R.
Определение и свойства квадрата
Квадрат — это частный случай ромба, параллелограмма или прямоугольника. Его отличие от этих фигур заключается в том, что все его углы прямые, и все четыре стороны равны. Квадрат — это правильный четырёхугольник.
Четырёхугольник называют квадратом в следующих случаях:
- Если это прямоугольник, у которого длина a и ширина b равны.
- Если это ромб с равными длинами диагоналей и с четырьмя прямыми углами.
К свойствам квадрата относятся все ранее рассмотренные свойства, относящиеся к прямоугольнику, а также следующие:
- Диагонали перпендикулярны относительно друг друга (свойство ромба).
- Точка пересечения совпадает с центром вписанной окружности.
- Обе диагонали делят четырёхугольник на четыре одинаковых прямоугольных и равнобедренных треугольника.
Приведём часто используемые формулы для  вычисления периметра, площади и элементов квадрата:
вычисления периметра, площади и элементов квадрата:
- Диагональ d = a √2.
- Периметр P = 4 a.
- Площадь S = a ².
- Радиус описанной окружности вдвое меньше диагонали: R = 0,5 a √2.
- Радиус вписанной окружности определяется как половинная длина стороны: r = a / 2.
Примеры вопросов и задач
Разберём некоторые вопросы, с которыми можно столкнуться при изучении курса математики в школе, и решим несколько простых задач.
Задача 1. Как изменится площадь прямоугольника, если увеличить длину его сторон в три раза?
Решение: Обозначим площадь исходной фигуры S0, а площадь четырёхугольника с утроенной длиной сторон — S1. По формуле, рассмотренной ранее, получаем: S0 = ab. Теперь увеличим длину и ширину в 3 раза и запишем: S1= 3 a • 3 b = 9 ab. Сравнивая S0 и S1, становится очевидно, что вторая площадь больше первой в 9 раз.
Вопрос 1. Четырёхугольник с прямыми углами — это квадрат?
Решение: Из определения следует, что фигура с прямыми углами является квадратом лишь тогда, когда длины всех его сторон равны. В остальных случаях фигура является прямоугольником.
Задача 2. Диагонали прямоугольника образуют угол 60 градусов. Ширина прямоугольника — 8. Рассчитать, чему равна диагональ.
Решение: Вспомним, что диагонали точкой пересечения разделяются пополам. Таким образом, имеем дело с равнобедренным треугольником с углом при вершине, равным 60°. Так как треугольник равнобедренный, то находящиеся при основании углы тоже будут одинаковы. Путём несложных вычислений получаем, что каждый из них равен 60°. Отсюда следует, что треугольник равносторонний. Ширина, известная нам, является основанием треугольника, следовательно, половина диагонали тоже равна 8, а длина целой диагонали в два раза больше и равна 16.
Вопрос 2. У прямоугольника все стороны равны или нет?
Решение: Достаточно вспомнить, что все стороны должны быть равны у квадрата, который является частным случаем прямоугольника. Во всех остальных случаях достаточное условие — это наличие минимум 3 прямых углов. Равенство сторон не является обязательным признаком.
Задача 3. Площадь квадрата известна и равна 289. Найти радиусы вписанной и описанной окружности.
 Решение: По формулам для квадрата проведём следующие расчёты:
Решение: По формулам для квадрата проведём следующие расчёты:
- Определим, чему равны основные элементы квадрата: a = √ S = √289 = 17, d = a √2 =1 7√2.
- Подсчитаем, чему равен радиус описанной вокруг четырёхугольника окружности: R = 0,5 d = 8,5√2.
- Найдём радиус вписанной окружности: r = a / 2 = 17 / 2 = 8,5.