Какого давление газа если в его объеме равном 1 см3 содержится 10 6 молекул
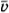
1
Сколько молекул содержится в 1 см3 воды? Какова масса молекулы воды? Каков приблизительный размер молекулы воды?
Ответ и решение
n = 3,33·1022 1/см3; m = 2,99·10-26 кг; a = 3,11·10-10 м.
Масса 1 моля воды составляет 18 г, а его объем V — 18 см3. В 1 моле воды содержится число молекул, равное постоянной Авогадро NА = 6·1023. Число молекул в 1 см3n = NА/V = 3,33·1022. Масса одной молекулы m = 18/NА = 3·10-26 кг. Объем V0 одной молекулы приблизительно равен 1/n см3. Тогда размер молекулы составит
.
2
Хорошо откачанная лампа накаливания объемом 10 см3 имеет трещину, в которую ежесекундно проникает миллион частиц газа. Сколько времени понадобится для наполнения лампы до нормального давления, если скорость проникновения газа остается постоянной? Температура 0 °С.
Ответ и решение
t ≈ 8,5 млн. лет.
Найдем число частиц газа, необходимое для наполнения лампы:
N = VNЛ = 10·2,69·1019 см3·см-3 = 2,69·1020,
где V – объем лампы, NЛ – постоянная Лошмидта.
Время, необходимое для наполнения лампы со скоростью v = 106 с-1, равно:
t = N/v = 2,69·1020/(106·с-1) = 2,69·1014 c ≈ 8,5 млн. лет.
3
За 10 суток полностью испарилось из стакана 100 г воды. Сколько в среднем вылетало молекул с поверхности воды за 1 с?
Ответ и решение
≈ 3,8·1018 молекул в секунду.
Переведем время t испарения воды из суток в секунды:
t = 10 сут. = 8,64·105 с.
Поскольку 1 моль воды имеет массу 18 г, то, используя постоянную Авогадро, можно найти число N молекул в 100 г воды:
N = NА·100/18 = 3,3·1024 шт.
Теперь найдем скорость v испарения воды:
v = N/t ≈ 3,8·1018 c-1.
4
В озеро средней глубиной 10 м и площадью 10 км2 бросили кристаллик поваренной соли NaCl массой 0,01 г. Сколько ионов хлора оказалось бы в наперстке воды объемом 2 см3, зачерпнутом из этого озера, если считать, что соль, растворившись, равномерно распределилась в озере?
Ответ и решение
≈ 2·106 ионов.
1 моль поваренной соли имеет массу 58,5 г, из которых 23 г — масса натрия, а 35,5 г — масса хлора. Чтобы рассчитать массу хлора в брошенном кристаллике хлора, решим систему из двух уравнений:
m(Na) + m(Cl) = 0,01
m(Na)/m(Cl) = 0,65
Из системы получим, m(Cl) = 6·10-3 г.
Теперь можно вычислить число частиц хлора N(Cl):
N(Cl) = NA· 6·10-3/35,5 ≈ 1020 ионов хлора.
Число ионов хлора в наперстке будет меньше полученного числа во столько раз, во сколько раз объем наперстка меньше объема озера. Найдем это число:
N = 1020·2·10-6/108 = 2·106 ионов хлора в наперстке.
5
Кристаллы поваренной соли NaCl кубической системы состоят из чередующихся атомов (ионов) Na и Cl.
Определить наименьшее расстояние между их центрами. Молярная масса поваренной соли ν = 58,5 г/моль, а ее плотность ρ = 2,2 г/см3.
Ответ и решение
r = 2,83·10-8 см.
Найдем сторону a куба, который занимает объем одного моля поваренной соли:
a = 
= 3 см.
Найдем, какое число ионов натрия и хлора приходится на одно ребро куба (общее число ионов натрия и хлора в 1 моле поваренной соли равно удвоенному числу молекул NaCl, т.е. 2NА):
n =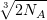 
≈ 108 ионов.
Теперь найдем расстояние между ионами:
l = a/n = 2,83·10-8 см.
6
Кубическая кристаллическая решетка железа содержит один атом железа на элементарный куб, повторяя который, можно получить всю решетку кристалла. Определить расстояние между ближайшими атомами железа, если плотность железа ρ = 7,9 г/см3, атомная масса А = 56.
Ответ и решение
2,3·10-8 см.
Найдем сторону a куба, который занимает объем одного моля железа:
a = = 1,9 см.
Найдем, какое число атомов железа приходится на одно ребро куба (общее число атомов железа в 1 моле равно NА):
n =
≈ 8,4·107 атомов.
Теперь найдем расстояние между атомами железа:
l = a/n = 2,3·10-8 см.
7
На пути молекулярного пучка стоит «зеркальная» стенка. Найти давление, испытываемое этой стенкой, если скорость молекул в пучке v = 103 м/с, концентрация n = 5·1017 1/м3, масса m = 3,32·10-27 кг. Рассмотреть три случая: а) стенка расположена перпендикулярно скорости пучка и неподвижна; б) пучок движется по направлению, составляющему со стенкой угол α = 45°; в) стенка движется навстречу молекулам со скоростью u = 50 м/с.
Ответ
а) pа ≈ 3,3·10-3 Па; б) pб ≈ 2,4·10-3 Па; в) pв ≈ pа.
8
Как изменилось бы давление в сосуде с газом, если бы внезапно исчезли силы притяжения между его молекулами?
Ответ
Учебник по физике
10 класс
При решении задач на применение молекулярно-кинетической теории идеального газа используются основное уравнение кинетической теории газов в форме (4.4.9) или (4.4.10) и вытекающие из него выражения для средней кинетической энергии молекул (4.5.5) и средней квадратичной скорости (4.7.2) или (4.7.3). Значительное количество задач удобно решать, используя формулу (4.5.6), связывающую давление газа с концентрацией молекул и абсолютной температурой. Внутренняя энергия идеальных одноатомных газов (например, инертных газов) вычисляется по формуле (4.8.1).
Задача 1
Чему равна масса газа, содержащегося в закрытом цилиндре вместимостью V = 0,5 л, если давление газа р = 5 • 105 Па, а средняя квадратичная скорость молекул 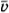= 500 м/с?
Решение. Согласно основному уравнению молекулярно-кинетической теории
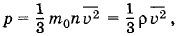
где ρ = m0n — плотность газа. Но ρ =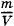 
, где m — масса газа, а V — его объем. Поэтому
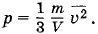
Откуда
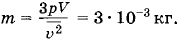
Задача 2
В воздухе при t = 27 °С взвешены пылинки сферической формы. Радиус пылинок r = 10-6 м. Плотность вещества пылинок ρ = 1,3 • 103 кг/м3. Определите средний квадрат скорости пылинок.
Решение. Пылинки принимают участие в броуновском движении. Средний квадрат скорости пылинки
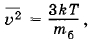
где mб — масса пылинки. Следовательно,
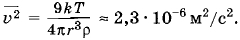
Задача 3
В сосуде находится 1 л воды при температуре 27 °С. Каким стало бы давление внутри сосуда, если бы силы взаимодействия между молекулами внезапно исчезли?
Решение. При исчезновении сил взаимодействия между молекулами вода превратилась бы в идеальный газ. Давление можно найти по уравнению состояния идеального газа:
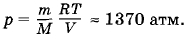
Задача 4
Два сосуда, содержащих различные газы, соединены трубкой с краном. Давление газа в первом сосуде p1, а число молекул N1. Давление газа во втором сосуде р2, число молекул N2. Какое давление установится в сосудах, если открыть кран соединительной трубки? Температуру считать постоянной.
Решение. Согласно формуле (4.5.6)
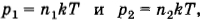
где
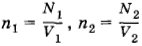
(здесь V1 и V2 — объемы сосудов). Следовательно,
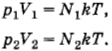
После того как кран будет открыт, давления выравняются и искомое давление согласно той же формуле (4.5.6) определится уравнением
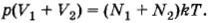
Подставляя сюда выражения для объемов из предыдущих формул, получим
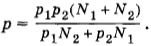
Задача 5
Плотность газа в баллоне газополной электрической лампы ρ = 0,9 кг/м3. При горении лампы давление в ней возросло с р1 = 8 • 104 Па до р2 = 1,1 • 105 Па. На сколько увеличилась при этом средняя квадратичная скорость молекул?
Решение. Плотность газа ρ = m0n, и основное уравнение мо-лекулярно-кинетической теории можно записать в форме
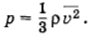
Поэтому
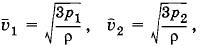
откуда
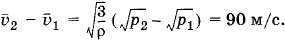
Упражнение З
- При какой температуре молекулы кислорода имеют такую же среднюю квадратичную скорость, что и молекулы азота при температуре 100 °С?
- На стенку площадью S налетает поток молекул со средней скоростью 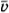. Число молекул, движущихся по направлению к стенке, в единице объема n0, масса каждой молекулы m0. Найдите действующую на стенку силу и давление, если молекулы движутся перпендикулярно стенке и удары молекул о стенку абсолютно неупругие.
- Какое давление на стенки сосуда производит водород, если число молекул в 1 см3 равно 4,1 • 1018, а средняя квадратичная скорость его молекул 2400 м/с?
- Определите число молекул кислорода в 1 м3, если давление равно 77 кПа, а средняя квадратичная скорость его молекул 400 м/с.
- Определите плотность газа, молекулы которого производят на стенки сосуда давление 1,6 • 105 Па. Средняя квадратичная скорость молекул 800 м/с.
- Какова средняя квадратичная скорость молекул газа, который занимает объем 1,3 м3 при давлении 5 • 104 Па? Масса газа 60 г.
- В цилиндре вместимостью 1,2 л содержится газ под давлением 105 Па. Среднее значение кинетической энергии каждой молекулы равно 6 • 10-21 Дж. Сколько молекул газа находится в цилиндре?
- Сколько молекул воздуха выходит из комнаты объемом V0 при повышении температуры от T1 до Т2? Атмосферное давление равно р0.
- Плотность смеси азота и водорода при температуре t = 47 °С и давлении р = 2 атм равна ρ = 0,3 г/л. Найдите концентрации молекул азота и водорода в смеси.
- Ампула объемом V = 1 см3, содержащая воздух при нормальных условиях, оставлена в космосе, где давление можно считать равным нулю. В ампуле проделано отверстие. Через какое время давление в ампуле станет равным нулю, если считать, что через отверстие каждую секунду вылетает 100 млн молекул?
- При повышении температуры идеального газа на 150 К средняя квадратичная скорость его молекул возросла с 400 до 500 м/с. На сколько надо нагреть этот газ, чтобы увеличить среднюю квадратичную скорость его молекул от 500 до 600 м/с?
- Изменится ли внутренняя энергия идеального газа при его изотермическом сжатии?
- Одноатомный газ, находящийся при постоянном давлении р = 2 • 106Па в цилиндре под поршнем площадью S = 160 см2, нагревается так, что поршень перемещается на расстояние Δh = 15 см. Найдите изменение внутренней энергии газа.