Какое свойство точек серединного перпендикуляра к отрезку вы знаете

Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.

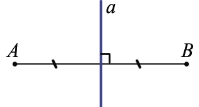
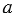— серединный перпендикуляр к отрезку АВ.

Теорема

Доказательство

1) Дано: m — серединный перпендикуляр отрезка АВ, О — середина АВ, М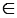m

Доказать: АМ = ВМ

Доказательство:

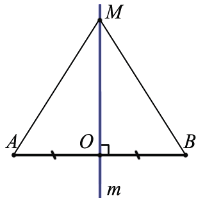
Если О = М, то АМ = ВМ, т.к. О — середина АВ.

Пусть О 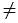М. Рассмотрим ОАМ и ОВМ: так как m — серединный перпендикуляр отрезка АВ, то рассматриваемые треугольники прямоугольные. ОА = ОВ, т.к. О — середина отрезка АВ, ОМ — общий катет, следовательно, ОАМ = ОВМ, по двум катетам, а в равных треугольниках против соответственно равных углов лежат равные стороны, поэтому АМ = ВМ.

2) Дано: m — серединный перпендикуляр отрезка АВ, О — середина АВ, АN = ВN

Доказать:N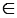m

Доказательство:

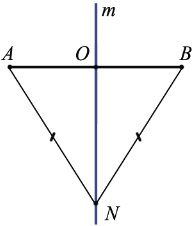
Рассмотрим произвольную точку N.

Если N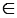АВ, то N = О, а, значит, она лежит на прямой m.

Если N не лежит на АВ, то ANB — равнобедренный, так как АN = ВN. О — середина АВ, следовательно, NО — медиана ANB, а, значит, и высота по свойству равнобедренного треугольника. Поэтому NО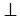АВ, следовательно, прямые NО и m совпадают, так как по устовию m — серединный перпендикуляр отрезка АВ, т.е. N — точка прямой m. Теорема доказана.

Следствие 1

Следствие2

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.