Какое свойство точек биссектрисы вы знаете

2 июня 2018

Сегодня будет очень лёгкий урок. Мы рассмотрим всего один объект — биссектрису угла — и докажем важнейшее её свойство, которое очень пригодится нам в будущем.

Только не надо расслабляться: иногда ученики, желающие получить высокий балл на том же ОГЭ или ЕГЭ, на первом занятии даже не могут точно сформулировать определение биссектрисы.

И вместо того, чтобы заниматься действительно интересными задачами, мы тратим время на такие простые вещи. Поэтому читайте, смотрите — и берите на вооружение.:)

Для начала немного странный вопрос: что такое угол? Правильно: угол — это просто два луча, выходящих из одной точки. Например:

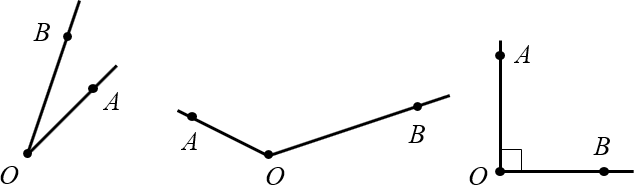Примеры углов: острый, тупой и прямой

Как видно из картинки, углы могут быть острыми, тупыми, прямыми — это сейчас неважно. Часто для удобства на каждом луче отмечают дополнительную точку и говорят, мол, перед нами угол $AOB$ (записывается как $angle AOB$).

Капитан очевидность как бы намекает, что помимо лучей $OA$ и $OB$ из точки $O$ всегда можно провести ещё кучу лучей. Но среди них будет один особенный — его-то и называют биссектрисой.

Определение. Биссектриса угла — это луч, который выходит из вершины этого угла и делит угол пополам.

Для приведённых выше углов биссектрисы будут выглядеть так:

Примеры биссектрис для острого, тупого и прямого угла

Поскольку на реальных чертежах далеко не всегда очевидно, что некий луч (в нашем случае это луч $OM$) разбивает исходный угол на два равных, в геометрии принято помечать равные углы одинаковым количеством дуг (у нас на чертеже это 1 дуга для острого угла, две — для тупого, три — для прямого).

Хорошо, с определением разобрались. Теперь нужно понять, какие свойства есть у биссектрисы.

Основное свойство биссектрисы угла

На самом деле у биссектрисы куча свойств. И мы обязательно рассмотрим их в следующем уроке. Но есть одна фишка, которую нужно понять прямо сейчас:

Теорема. Биссектриса угла — это геометрическое место точек, равноудалённых от сторон данного угла.

В переводе с математического на русский это означает сразу два факта:

1. Всякая точка, лежащая на биссектрисе некого угла, находится на одинаковом расстоянии от сторон этого угла.
2. И наоборот: если точка лежит на одинаковом расстоянии от сторон данного угла, то она гарантированно лежит на биссектрисе этого угла.

Прежде чем доказывать эти утверждения, давайте уточним один момент: а что, собственно, называется расстоянием от точки до стороны угла? Здесь нам поможет старое-доброе определение расстояния от точки до прямой:

Определение. Расстояние от точки до прямой — это длина перпендикуляра, проведённого из данной точки к этой прямой.

Например, рассмотрим прямую $l$ и точку $A$, не лежащую на этой прямой. Проведём перпендикуляр $AH$, где $Hin l$. Тогда длина этого перпендикуляра и будет расстоянием от точки $A$ до прямой $l$.

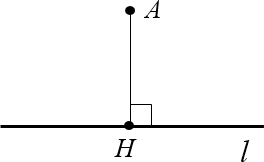Графическое представление расстояния от точки до прямой

Поскольку угол — это просто два луча, а каждый луч — это кусок прямой, легко определить расстояние от точки до сторон угла. Это просто два перпендикуляра:

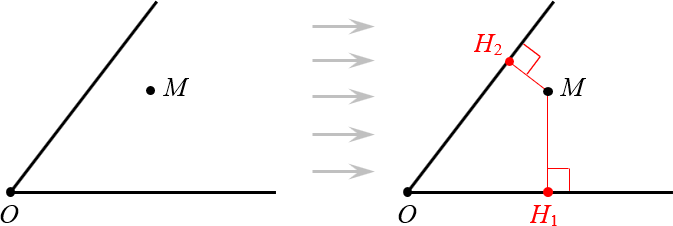Определяем расстояние от точки до сторон угла

Вот и всё! Теперь мы знаем, что такое расстояние и что такое биссектриса. Поэтому можно доказывать основное свойство.

Как и обещал, разобьём доказательство на две части:

1. Расстояния от точки на биссектрисе до сторон угла одинаковы

Рассмотрим произвольный угол с вершиной $O$ и биссектрисой $OM$:

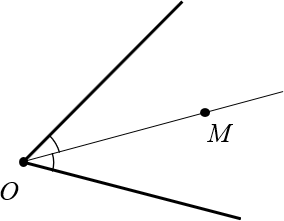
Докажем, что эта самая точка $M$ находится на одинаковом расстоянии от сторон угла.

Доказательство. Проведём из точки $M$ перпендикуляры к сторонам угла. Назовём их $M{{H}_{1}}$ и $M{{H}_{2}}$:

Провели перпендикуляры к сторонам угла

Получили два прямоугольных треугольника: $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$. У них общая гипотенуза $OM$ и равные углы:

1. $angle MO{{H}_{1}}=angle MO{{H}_{2}}$ по условию (поскольку $OM$ — биссектриса);
2. $angle M{{H}_{1}}O=angle M{{H}_{2}}O=90{}^circ $ по построению;
3. $angle OM{{H}_{1}}=angle OM{{H}_{2}}=90{}^circ -angle MO{{H}_{1}}$, поскольку сумма острых углов прямоугольного треугольника всегда равна 90 градусов.

Следовательно, треугольники равны по стороне и двум прилежащим углам (см. признаки равенства треугольников). Поэтому, в частности, $M{{H}_{2}}=M{{H}_{1}}$, т.е. расстояния от точки $O$ до сторон угла действительно равны. Что и требовалось доказать.:)

2. Если расстояния равны, то точка лежит на биссектрисе

Теперь обратная ситуация. Пусть дан угол $O$ и точка $M$, равноудалённая от сторон этого угла:

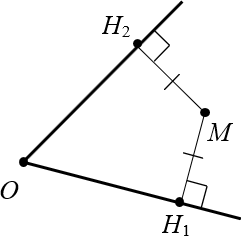
Докажем, что луч $OM$ — биссектриса, т.е. $angle MO{{H}_{1}}=angle MO{{H}_{2}}$.

Доказательство. Для начала проведём этот самый луч $OM$, иначе доказывать будет нечего:

Провели луч $OM$ внутри угла

Снова получили два прямоугольных треугольника: $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$. Очевидно, что они равны, поскольку:

1. Гипотенуза $OM$ — общая;
2. Катеты $M{{H}_{1}}=M{{H}_{2}}$ по условию (ведь точка $M$ равноудалена от сторон угла);
3. Оставшиеся катеты тоже равны, т.к. по теореме Пифагора $OH_{1}^{2}=OH_{2}^{2}=O{{M}^{2}}-MH_{1}^{2}$.

Следовательно, треугольники $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$ по трём сторонам. В частности, равны их углы: $angle MO{{H}_{1}}=angle MO{{H}_{2}}$. А это как раз и означает, что $OM$ — биссектриса.

В заключение доказательства отметим красными дугами образовавшиеся равные углы:

Биссектриса разбила угол $angle {{H}_{1}}O{{H}_{2}}$ на два равных

Как видите, ничего сложного. Мы доказали, что биссектриса угла — это геометрическое место точек, равноудалённых до сторон этого угла.:)

Теперь, когда мы более-менее определились с терминологией, пора переходить на новый уровень. В следующем уроке мы разберём более сложные свойства биссектрисы и научимся применять их для решения настоящих задач.

Смотрите также:

1. Высота в треугольнике
2. Основное свойство биссектрисы угла в треугольнике и его применение для решения задач
3. Тест к уроку «Площади многоугольников на координатной сетке» (легкий)
4. Правила вычисления производных
5. Сводный тест по задачам B15 (2 вариант)
6. Симметрия корней и оптимизация ответов в тригонометрии