Какое свойство тела называют инертностью

Взаимодействие тел, инертность, масса
Из наблюдений можно заметить, что тела изменяют свою скорость только при наличии не скомпенсированного действия. Т. к. быстрота изменения скорости характеризуется ускорением тела, можем заключить, что причиной ускорения является некомпенсированное действие одного тела на другое. Но одно тело не может действовать на другое, не испытывая его действия на себе. Следовательно, ускорение появляется при взаимодействии тел. Ускорение приобретают оба взаимодействующие тела. Так же из наблюдений можно установить ещё один факт: при одинаковом действии разные тела приобретают разные ускорения.
Установились считать: чем меньше ускорение приобретает тело при взаимодействии, тем инертнее это тело.
Инертность – это свойство тела сохранять свою скорость постоянной (то же, что и инерция). Проявляет себя в том, что для изменения скорости тела требуется некоторое время. Процесс изменения скорости не может быть мгновенным.
Например, движущийся по дороге автомобиль не может мгновенно остановиться, для уменьшения скорости требуется некоторое время, а за это время он успевает переместиться на довольно большое расстояние (десятки метров). (Осторожно переходите дорогу!!!)
Мерой инертности является инертная масса.
Масса (инертная) – мера инертности тела.
Чем инертнее тело, тем больше его масса. Чем больше инертность, тем меньше ускорение. Следовательно, чем больше масса тела, тем меньше его ускорение: a∼1mboxed{asimfrac 1m}.
Данная зависимость записана единственно правильным способом, т. к. форма m∼1am sim frac 1a не верна. Масса не может зависеть от ускорения, она является свойством тела, а ускорение является характеристикой состояния движения тела.
Данная зависимость подтверждается многочисленными опытными результатами.
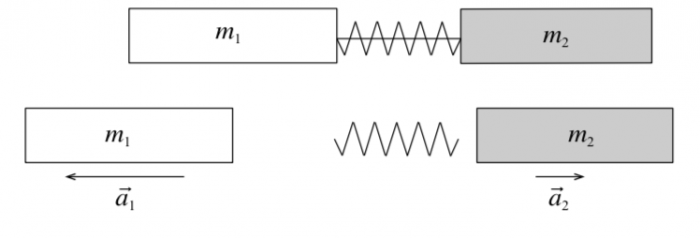
Рис. 2 Измерение массы методом взаимодействия тел.
Два тела, скреплённые между собой сжатой пружиной, после пережигания нити, удерживающей пружину, начинают двигаться не которое время с ускорением (рис. 1) . Опыт показывает, что при любых взаимодействиях данных двух тел отношение ускорений тел равно обратному отношению их масс:
[frac{a_1}{a_2} = frac{m_2}{m_1};]
если взять первую массу за эталонную (m1=mэтm_1 = m_mathrm{эт}), то m2=mэтaэтa2m_2 = m_mathrm{эт}frac{a_mathrm{эт}}{a_2}.
Масса, измеренная путём взаимодействия (измерения ускорения), называется инертной.
Измерение массы методом взвешивания тел.
Второй способ измерения масс основан на сравнении действия Земли на различные тела. Такое сравнение можно осуществить либо последовательно (сначала определяют растяжение пружины под действием эталонных масс, а потом под действием исследуемого тела в тех же условиях), либо одновременно располагают на равноплечих рычажных весах на одной чаше исследуемое тело, а на другой эталонные массы (рис. 2).
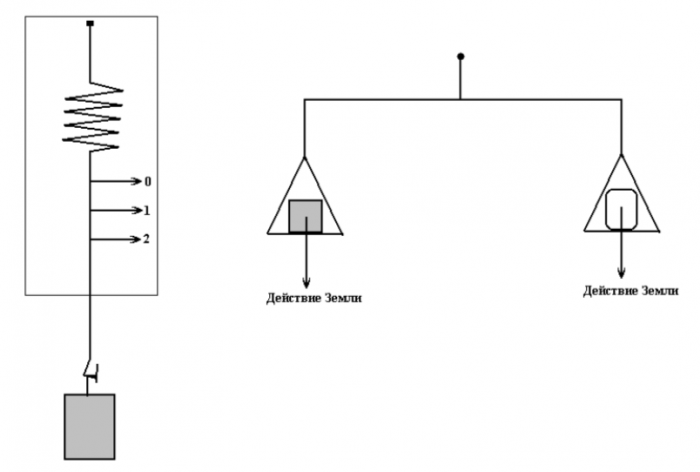
Рис. 2
 |
| Рис. 3 |
Масса, измеренная путём взвешивания, называется гравитационной.
В качестве эталона и той и другой массы принята масса тела, выполненного в форме цилиндра высотой 39 мм39 mathrm{мм} и диаметром 39 мм39 mathrm{мм}, изготовленного из сплава 10 % иридия и 90 % платины (рис. 3).
В 1971 г наши соотечественники Брагинский и Панов придумали и провели опыт по сравнению массы гравитационной и инертной. Оказалось, что с точностью до 10-1210^{-12} % эти массы равны.
Данный факт известен был и ранее, и послужил основанием для формулировки Эйнштейном принципа эквивалентности.
Принцип эквивалентности утверждает, что
1) ускорение, вызванное гравитационным взаимодействием в малой области пространства, и за небольшой интервал времени, неотличимо от ускоренно движущейся системы отсчёта.
2) ускоренно движущееся тело эквивалентно неподвижному телу, находящемуся в гравитационном поле.
Пример 1.
Два тела массами 400 г400 mathrm{г} и 600 г600 mathrm{г} двигались навстречу друг другу и после удара остановились. Какова скорость второго тела, если первое двигалось со скоростью 3 м/с3 mathrm{м}/mathrm{с}?
Решение.
Сила, возникающая при взаимодействии тел, конечно же, не остаётся постоянной, и ускорения тоже. Мы будем считать, что и силы, и ускорения принимают некоторы е средние значения, причём одинаковые для любого момента времени. Отношение ускорений тел равно обратному отношению их масс: a1a2=m2m1frac{a_1}{a_2} = frac{m_2}{m_1}. В свою очередь, ускорение равно отношению изменения скорости ко времени изменения. Конечные скорости тел равны нулю, а время взаимодействия одинаково для обоих тел:
[frac{m_2}{m_1} = frac{a_1}{a_2} = frac{frac{Delta v_1}{Delta t}}{frac{Delta v_2}{Delta t}} = frac{v_mathrm{к1}-v_{01}}{v_mathrm{к2}-v_{02}} = frac{v_{01}}{v_{02}},]
откуда получим искомую скорость: v02=m1m2·v01.v_{02} = frac{m_1}{m_2}cdot v_{01}.
Количественно ответ будет таким: v02=0,4 кг0,6 кг·3 мс=2 мсv_{02} = frac{0,4 mathrm{кг}}{0,6 mathrm{кг}}cdot 3 frac{mathrm{м}}{mathrm{с}} = 2 frac{mathrm{м}}{mathrm{с}}.
§ 02-б. Свойство инертности и масса тела
Когда мы играем с мячом, нам кажется, что стоит его ударить рукой или ногой, и он мгновенно полетит в нужную сторону. Если же мяч налетит на стену, то в тот же миг отскочит назад. Похоже на правду?
Проверим наше мнение кинематографическим методом: заснимем движение мяча на киноплёнку и рассмотрим его положения на получившихся кадрах (см. рисунок).
Вот мяч приближается к стене (кадр 1). Вот он её касается (2), значит, на следующем кадре мяч должен полететь обратно. Нет! Мяч летит дальше, сплющиваясь всё сильнее (3). И на следующем кадре мяч всё плотнее приближается к стене (4). И лишь после этого, распрямляясь, летит обратно (кадры 5–7). Как видите, мяч не мгновенно меняет скорость, останавливаясь при ударе и разгоняясь в обратном направлении.
Не только упругий мяч, но и вообще любое тело не мгновенно изменяет свою скорость – для этого всегда требуется некоторое время. Например, нагруженный самосвал дольше разгоняется и тормозит, чем тот же самосвал, но без груза.
В физике свойство тела сопротивляться мгновенному изменению направления и/или быстроты движения, то есть изменению скорости, называют инертностью тела. Для изменения скорости тела с большей массой нужно больше времени, то есть инертность тела проявляется тем заметнее, чем больше его масса.
Как вы понимаете, гравитационное притяжение и инертность тела – это совершенно разные свойства. Для их характеристики правильнее было бы использовать две разные физические величины: гравитационную массу и инертную массу. Однако эксперименты не обнаружили их различия, что позволяет нам оба этих свойства каждого тела характеризовать одной величиной – массой.
Мы знаем, как измерять массу методом взвешивания с помощью весов (см. § 2-а). Однако свойство инертности позволяет измерять массу другим способом – методом взаимодействия. Его суть заключается в сравнении инертных свойств изучаемого тела и инертных свойств гирь.
Рассмотрим опыт. Имеются две одинаковые тележки с упругими пластинками; на левой тележке находится «взвешиваемое» тело, а на правой – гири. Подкатим тележки друг к другу, согнув пластинки между ними и перевязав их тонкой нитью. Если её пережечь, пластинки начнут распрямляться, отталкивая друг друга. При этом тележки разъедутся в стороны, приобретя некоторые скорости. Говорят, что произошло взаимодействие тележек.
Если масса гирь на правой тележке мала, то за время взаимодействия она приобретёт большую скорость, чем тележка с телом. И наоборот: при избыточной массе гирь скорость тележки с ними будет меньше, чем скорость тележки с телом. Подбирая массу гирь, можно заставить тележки разъезжаться с одинаковыми скоростями. Это значит, что в этом случае масса тела равна массе гирь. Подсчитав массу гирь, мы найдём массу тела.
Весами и методом взвешивания мы не можем воспользоваться в условиях невесомости, поскольку ни тело, ни гири не будут давить на чаши весов. Однако метод взаимодействия в этом случае вполне применим, так как даже в условиях невесомости можно наблюдать взаимодействие тележек и сравнивать их скорости.
Источник
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Подробности
Просмотров: 539
«Физика — 10 класс»
Инертность тела.
Мы уже говорили о явлении инерции.
Именно вследствие инерции покоящееся тело приобретает заметную скорость под действием силы не сразу, а лишь за некоторый интервал времени.
Инертность — свойство тел по-разному изменять свою скорость под действием одной и той же силы.
Ускорение возникает сразу, одновременно с началом действия силы, но скорость нарастает постепенно.
Даже очень большая сила не в состоянии сообщить телу сразу значительную скорость.
Для этого нужно время.
Чтобы остановить тело, опять-таки нужно, чтобы тормозящая сила, как бы она ни была велика, действовала некоторое время.
Именно эти факты имеют в виду, когда говорят, что тела инертны, т. е. одним из свойств тела является инертность.
Масса.
Количественной мерой инертности является масса.

Приведём примеры простых опытов, в которых очень отчётливо проявляется инертность тел.
1. На рисунке 2.4 изображён массивный шар, подвешенный на тонкой нити.
Внизу к шару привязана точно такая же нить.
Если медленно тянуть за нижнюю нить, то порвётся верхняя нить: ведь на неё действуют и шар своей тяжестью, и сила, с которой мы тянем шар вниз.
Однако если за нижнюю нить очень быстро дёрнуть, то оборвётся именно она, что на первый взгляд довольно странно.
Но это легко объяснить.
Когда мы тянем за нить медленно, то шар постепенно опускается, растягивая верхнюю нить до тех пор, пока она не оборвётся.
При быстром рывке с большой силой шар получает большое ускорение, но скорость его не успевает увеличиться сколько-нибудь значительно за тот малый промежуток времени, в течение которого нижняя нить сильно растягивается и обрывается.
Верхняя нить поэтому мало растягивается и остаётся целой.

2. Интересен опыт с длинной палкой, подвешенной на бумажных кольцах (рис. 2.5).
Если резко ударить по палке железным стержнем, то палка ломается, а бумажные кольца остаются невредимыми.
3. Наконец, самый, пожалуй, эффектный опыт.
Если выстрелить в пустой пластмассовый сосуд, пуля оставит в стенках правильные отверстия, но сосуд останется целым.
Если же выстрелить в такой же сосуд, заполненный водой, то сосуд разорвётся на мелкие части.
Это объясняется тем, что вода малосжимаема и небольшое изменение её объёма приводит к резкому возрастанию давления.
Когда пуля очень быстро входит в воду, пробив стенку сосуда, давление резко возрастает.
Из-за инертности воды её уровень не успевает повыситься, и возросшее давление разрывает сосуд на части.
Чем больше масса тела, тем больше его инертность, тем сложнее вывести тело из первоначального состояния, т. е. заставить его двигаться или, наоборот, остановить его движение.
Единица массы.
В кинематике мы пользовались двумя основными физическими величинами — длиной и временем.
Для единиц этих величин установлены соответствующие эталоны, сравнением с которыми определяются любая длина и любой интервал времени.
Единицей длины является метр, а единицей времени — секунда.
Все другие кинематические величины не имеют эталонов единиц.
Единицы таких величин называются производными.
При переходе к динамике мы должны ввести ещё одну основную единицу и установить её эталон.
В Международной системе единиц (СИ) за единицу массы — один килограмм (1 кг) — принята масса эталонной гири из сплава платины и иридия, которая хранится в Международном бюро мер и весов в Севре, близ Парижа.
Точные копии этой гири имеются во всех странах.
Приближённо массу 1 кг имеет вода объёмом 1 л при комнатной температуре.
Легко осуществимые способы сравнения любой массы с массой эталона путём взвешивания мы рассмотрим позднее.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Динамика — Физика, учебник для 10 класса — Класс!ная физика
Основное утверждение механики —
Сила —
Инертность тела. Масса. Единица массы —
Первый закон Ньютона —
Второй закон Ньютона —
Принцип суперпозиции сил —
Примеры решения задач по теме «Второй закон Ньютона» —
Третий закон Ньютона —
Геоцентрическая система отсчёта —
Принцип относительности Галилея. Инвариантные и относительные величины —
Силы в природе —
Сила тяжести и сила всемирного тяготения —
Сила тяжести на других планетах —
Примеры решения задач по теме «Закон всемирного тяготения» —
Первая космическая скорость —
Примеры решения задач по теме «Первая космическая скорость» —
Вес. Невесомость —
Деформация и силы упругости. Закон Гука —
Примеры решения задач по теме «Силы упругости. Закон Гука» —
Силы трения —
Примеры решения задач по теме «Силы трения» —
Примеры решения задач по теме «Силы трения» (продолжение) —
Классификация динамических характеристик движений человека
Вращательное движение тела
Мерой изменения положения тела при вращательном движении является угол поворота фи. Чтобы знать положение тела во вращательном движении в любой момент времени, надо знать зависимость угла поворота фи от времени: фи = фи(t).
Данное уравнение выражает закон вращательного движения тела. Основными кинематическими характеристиками вращательного движения тела являются его угловая скорость (ω) и угловое ускорение (e).
При вращательном движении тела разные его точки имеют различные линейные скорости и ускорения. Линейная скорость точки вращающегося тела численно равна произведению угловой скорости на радиус вращения и направлена по касательной к окружности вращения (перпендикулярно радиусу вращения R): V= ωR.
Таким образом, линейные скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения (чем дальше удалена точка от оси вращения, тем большую линейную скорость она имеет).
Пример.При выполнении гимнастом большого оборота на перекладине линейная скорость точки, расположенной в области тазобедренного сустава составляет 10,8 м/с, а точки, расположенной в области голеностопного сустава – 18,0 м/с.
В таблице 3.2. представлена взаимосвязь кинематических характеристик при поступательном и вращательном движениях тела.
Таблица 3.2.
Взаимосвязь показателей при поступательном и вращательном движении тела (Н.Б. Кичайкина, 2000)
| Поступательное движение | Вращательное движение | Взаимосвязь показателей |
| Линейная скорость (м/c), V | Угловая скорость (рад/c), ω | V=ω R |
| Линейное ускорение (м/c2), a | Угловое ускорение (рад/c2), e | а=e R |
Скорость движений человека и движимых им тел изменяются под действием сил. Чтобы раскрыть механизм движений (причины их возникновения и направленность их изменений) исследуют динамические характеристики. К ним относятся:
· инерционные характеристики (особенности тела человека и движимых им тел);
· силовые(особенности взаимодействия звеньев тела и других тел);
· энергетические(характеристики состояния систем).
Разные тела изменяют скорость под действием сил по-разному. Это свойство тел называется инертностью.
Инертность – свойство физических тел, от которого зависит величина получаемых ускорений при их взаимодействии.
Инерционные характеристики – это характеристики тела или системы тел. Среди инерционных характеристик различают: массу тела и момент инерции тела.
Масса тела (m) – мера инертности тела при поступательном движении. Она измеряется отношением величины приложенной силы к вызываемому ею ускорению: m=F/a,
где: m – масса; F– сила; a – ускорение.
Масса тела зависит от количества вещества, которым обладает тело и характеризует его свойство – как именно приложенная сила может изменить его движение. Одна и та же сила вызовет большее ускорение у тела с меньшей массой, чем у тела с большей массой.
В атлетизме при тренировке спортсмены используют штангу различной массы. Из личного опыта им известно, что придать штанге, имеющей большую массу ускорение значительно сложнее, чем штанге маленькой массы.
В случае вращательного движения мало знать массу тела, важно еще знать распределение масс относительно оси вращения. Например, фигурист при вращении прижимает руки к туловищу, а затем разводит их в стороны. Общая масса системы при этом не изменяется, а распределение масс становится другим, и это сказывается на движении, оно замедляется (Н.Б. Кичайкина, 2000). В механике существует характеристика, определяющая меру инертности тела во вращательном движении – момент инерции тела.
Момент инерции тела (J ) – мера инертности твердого тела при вращательном движении.
Момент инерции зависит от распределения массы относительно оси вращения. Его достаточно легко найти для простых геометрических фигур (шар, цилиндр и др.), но определить его в многозвенной системе тела человека при различных позах непросто.
Инертностью тела называют свойство тела:
изменять свою скорость под действием других тел |
сохранять свою скорость при отсутствии действия на него других тел |
сохранять свою форму при отсутствии действия на него других тел |
Закон инерции сформулировал:
И. Ньютон |
Г. Галилей |
Л. Эйлер |
Аристотель |
Инерциальными называют системы отсчёта:
в которых выполняется закон инерции |
относительно которых тело движется равномерно и прямолинейно |
в которых не выполняется закон инерции |
относительно которых тело движется равноускоренно |
Автомобиль движется равномерно и прямолинейно со скоростью $vec{v}$. Равнодействующая сил, приложенных к автомобилю, имеет направление:

1 |
2 |
3 |
равнодействующая равна нулю |
Неинерциальными называют системы отсчёта:
в которых не выполняется закон инерции |
относительно которых тело движется равнозамедленно |
относительно которых тело движется равномерно и прямолинейно |
в которых выполняется закон инерции |
Впишите ответ.
Автомобиль массой 1500 кг начинает двигаться горизонтально с ускорением 0,5 м/с$^{2}$. Сопротивление движению 500 Н. сила тяги, развиваемая двигателем, равна:
Н.
Соотнесите систему отсчёта и изображение, описывающее её.
Впишите в текст пропущенные слова.
Ускорение тела
пропорционально действующей силе, приложенной к телу, и
пропорционально его массе.
