Какое свойство тел называют инерцией

Взаимодействие тел, инертность, масса
Из наблюдений можно заметить, что тела изменяют свою скорость только при наличии не скомпенсированного действия. Т. к. быстрота изменения скорости характеризуется ускорением тела, можем заключить, что причиной ускорения является некомпенсированное действие одного тела на другое. Но одно тело не может действовать на другое, не испытывая его действия на себе. Следовательно, ускорение появляется при взаимодействии тел. Ускорение приобретают оба взаимодействующие тела. Так же из наблюдений можно установить ещё один факт: при одинаковом действии разные тела приобретают разные ускорения.
Установились считать: чем меньше ускорение приобретает тело при взаимодействии, тем инертнее это тело.
Инертность – это свойство тела сохранять свою скорость постоянной (то же, что и инерция). Проявляет себя в том, что для изменения скорости тела требуется некоторое время. Процесс изменения скорости не может быть мгновенным.
Например, движущийся по дороге автомобиль не может мгновенно остановиться, для уменьшения скорости требуется некоторое время, а за это время он успевает переместиться на довольно большое расстояние (десятки метров). (Осторожно переходите дорогу!!!)
Мерой инертности является инертная масса.
Масса (инертная) – мера инертности тела.
Чем инертнее тело, тем больше его масса. Чем больше инертность, тем меньше ускорение. Следовательно, чем больше масса тела, тем меньше его ускорение: a∼1mboxed{asimfrac 1m}.
Данная зависимость записана единственно правильным способом, т. к. форма m∼1am sim frac 1a не верна. Масса не может зависеть от ускорения, она является свойством тела, а ускорение является характеристикой состояния движения тела.
Данная зависимость подтверждается многочисленными опытными результатами.
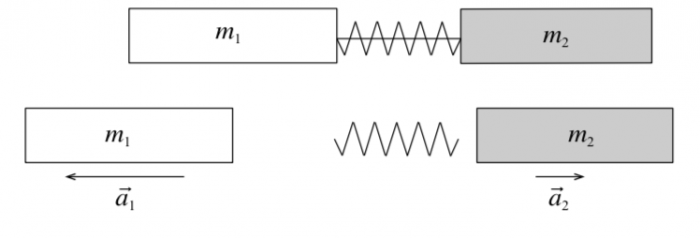
Рис. 2 Измерение массы методом взаимодействия тел.
Два тела, скреплённые между собой сжатой пружиной, после пережигания нити, удерживающей пружину, начинают двигаться не которое время с ускорением (рис. 1) . Опыт показывает, что при любых взаимодействиях данных двух тел отношение ускорений тел равно обратному отношению их масс:
[frac{a_1}{a_2} = frac{m_2}{m_1};]
если взять первую массу за эталонную (m1=mэтm_1 = m_mathrm{эт}), то m2=mэтaэтa2m_2 = m_mathrm{эт}frac{a_mathrm{эт}}{a_2}.
Масса, измеренная путём взаимодействия (измерения ускорения), называется инертной.
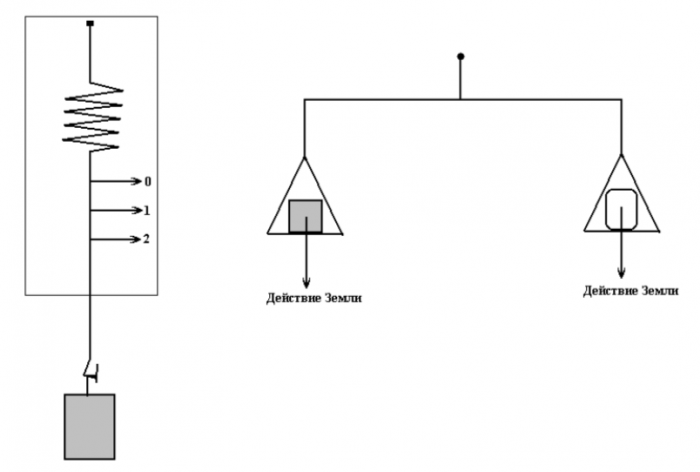
Измерение массы методом взвешивания тел.
Второй способ измерения масс основан на сравнении действия Земли на различные тела. Такое сравнение можно осуществить либо последовательно (сначала определяют растяжение пружины под действием эталонных масс, а потом под действием исследуемого тела в тех же условиях), либо одновременно располагают на равноплечих рычажных весах на одной чаше исследуемое тело, а на другой эталонные массы (рис. 2).

Рис. 2
 |
| Рис. 3 |
Масса, измеренная путём взвешивания, называется гравитационной.
В качестве эталона и той и другой массы принята масса тела, выполненного в форме цилиндра высотой 39 мм39 mathrm{мм} и диаметром 39 мм39 mathrm{мм}, изготовленного из сплава 10 % иридия и 90 % платины (рис. 3).
В 1971 г наши соотечественники Брагинский и Панов придумали и провели опыт по сравнению массы гравитационной и инертной. Оказалось, что с точностью до 10-1210^{-12} % эти массы равны.
Данный факт известен был и ранее, и послужил основанием для формулировки Эйнштейном принципа эквивалентности.
Принцип эквивалентности утверждает, что
1) ускорение, вызванное гравитационным взаимодействием в малой области пространства, и за небольшой интервал времени, неотличимо от ускоренно движущейся системы отсчёта.
2) ускоренно движущееся тело эквивалентно неподвижному телу, находящемуся в гравитационном поле.
Пример 1.
Два тела массами 400 г400 mathrm{г} и 600 г600 mathrm{г} двигались навстречу друг другу и после удара остановились. Какова скорость второго тела, если первое двигалось со скоростью 3 м/с3 mathrm{м}/mathrm{с}?
Решение.
Сила, возникающая при взаимодействии тел, конечно же, не остаётся постоянной, и ускорения тоже. Мы будем считать, что и силы, и ускорения принимают некоторы е средние значения, причём одинаковые для любого момента времени. Отношение ускорений тел равно обратному отношению их масс: a1a2=m2m1frac{a_1}{a_2} = frac{m_2}{m_1}. В свою очередь, ускорение равно отношению изменения скорости ко времени изменения. Конечные скорости тел равны нулю, а время взаимодействия одинаково для обоих тел:
[frac{m_2}{m_1} = frac{a_1}{a_2} = frac{frac{Delta v_1}{Delta t}}{frac{Delta v_2}{Delta t}} = frac{v_mathrm{к1}-v_{01}}{v_mathrm{к2}-v_{02}} = frac{v_{01}}{v_{02}},]
откуда получим искомую скорость: v02=m1m2·v01.v_{02} = frac{m_1}{m_2}cdot v_{01}.
Количественно ответ будет таким: v02=0,4 кг0,6 кг·3 мс=2 мсv_{02} = frac{0,4 mathrm{кг}}{0,6 mathrm{кг}}cdot 3 frac{mathrm{м}}{mathrm{с}} = 2 frac{mathrm{м}}{mathrm{с}}.
Ине́рция (от лат. inertia — покой, бездеятельность, постоянство, неизменность) — свойство тела оставаться в некоторых системах отсчёта в состоянии покоя или равномерного прямолинейного движения в отсутствие внешних воздействий[1][2], а также препятствовать изменению своей скорости (как по модулю, так и по направлению[3]) при наличии внешних сил за счёт своей инертной массы.
Понятию «инерция» синонимично одно из значений понятия инертность[1] (другие значения последнего не относятся к физике).
Количественно соотношение между воздействием на тело и изменением его движения даётся формулой второго закона Ньютона[4]:
.
Здесь — сила, действующая на тело, — инертная масса, — скорость тела.
С понятием инерции связано понятие инерциальных систем отсчёта.
Формулировка[править | править код]
Существование инерциальных систем отсчёта в классической механике постулируется первым законом Нью́тона, который также называется зако́ном ине́рции. Его классическую формулировку дал Ньютон в своей книге «Математические начала натуральной философии»:
Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.
Современная, более точная, формулировка закона:
Системы отсчёта, в которых выполняется закон инерции, называют инерциальными системами отсчёта (ИСО). Все другие системы отсчёта (например, вращающиеся или движущиеся с ускорением) называются соответственно неинерциальными.
В неинерциальных системах отсчёта закон инерции не выполняется. Тем не менее движение тел в неинерциальных системах отсчёта можно описывать теми же уравнениями движения, что и в инерциальных, если наряду с силами, обусловленными воздействием тел друг на друга, учитывать силы инерции[5][6].
История[править | править код]
Древнегреческие учёные, судя по дошедшим до нас сочинениям, размышляли о причинах совершения и прекращения движения. В «Физике» Аристотеля (IV век до н. э.) приводится такое рассуждение о движении в пустоте[7]:
Однако в другом труде «Механика», приписываемом Аристотелю, утверждается[8]:
Наблюдения действительно показывали, что тело останавливалось при прекращении действия толкающей его силы. Естественное противодействие внешних сил (трения, сопротивления воздуха и т. п.) движению толкаемого тела при этом не учитывалось. Поэтому Аристотель связывал неизменность скорости движения любого тела с неизменностью прилагаемой к нему силы.
Только через два тысячелетия Галилео Галилей (1564—1642) смог исправить эту ошибку «аристотелевской физики». В своем труде «Беседы о двух новых науках» Галилей писал[8]:
Это суждение нельзя вывести непосредственно из эксперимента, так как невозможно исключить все внешние влияния (трение и т. п.). Поэтому, здесь Галилей впервые применил метод логического мышления, базирующийся на непосредственных наблюдениях и подобный математическому методу доказательства «от противного». Если наклон плоскости к горизонтали является причиной ускорения тела, движущегося по ней вниз, и замедления тела, движущегося по ней вверх, то при движении по горизонтальной плоскости у тела нет причин ускоряться или замедляться — и оно должно пребывать в состоянии равномерного движения или покоя.
Таким образом, Галилей просто и ясно доказал связь между силой и изменением скорости (ускорением), а не между силой и самой скоростью, как считали Аристотель и его последователи. Это открытие Галилея вошло в науку как закон инерции. Однако, Галилей допускал свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений). В 1638 году итальянец Балиани уточнил закон инерции, указав, что при полном отсутствии внешних воздействий естественной траекторией движения тела является прямая. В современном виде закон инерции сформулировал Декарт. Ньютон включил закон инерции в свою систему законов механики как первый закон.
Смежные понятия[править | править код]
Принцип относительности Галилея: во всех инерциальных системах отсчёта все механические процессы протекают одинаково (если начальные условия для всех тел одинаковы). В системе отсчёта, приведённой в состояние покоя или равномерного прямолинейного движения относительно инерциальной системы отсчёта (условно — «покоящейся»), все процессы протекают точно так же, как и в покоящейся системе.
Следует отметить, что понятие инерциальной системы отсчёта — абстрактная модель, то есть некий идеальный объект, рассматриваемый вместо реального объекта (другими примерами абстрактной модели служат абсолютно твёрдое тело или нерастяжимая невесомая нить). Реальные системы отсчёта всегда связаны с каким-либо объектом или объектами, и соответствие реально наблюдаемого движения тел в таких системах результатам расчётов будет неполным. В то же время точность подобной абстракции в земных условиях весьма велика.
Инертная масса — мера инертности тела в физике, показатель того, в большей или меньшей степени данное тело будет препятствовать изменению своей скорости относительно инерциальной системы отсчёта при воздействии внешних сил. Инертная масса фигурирует в выражении второго закона Ньютона, являющегося важнейшим законом классической механики.
См. также[править | править код]
- Законы Ньютона
- Сила инерции
- Момент инерции
- Принцип Маха
- Механика
- Гистерезис
- Теория импетуса
- Инертная масса
Примечания[править | править код]
- ↑ 1 2 3 Инерция // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 146. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- ↑ Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
- ↑ Т.И.Трофимов. Физика. — Москва: «Академия», 2012.
- ↑ Коноплёва Н. П. Об эволюции понятия инерции (Ньютон, Мах, Эйнштейн) // Эйнштейновский сборник 1975-1976. — М., Наука, 1978. — с. 216-244
- ↑ Савельев И. В. Курс общей физики. Т. 1. Механика. Молекулярная физика. — М.: Наука, 1987. — С. 118—119.
- ↑ Ландсберг Г. С. Элементарный учебник физики. Том 1. Механика. Теплота. Молекулярная физика. — М.: Наука, 1975. — C. 292
- ↑ Физика (Аристотель)/Книга 4/Глава 8
- ↑ 1 2 Эйнштейн А., Инфельд Л. Эволюция физики. — М.: Наука, 1965. — С. 10-12.
Литература[править | править код]
- Лич Дж. У. Классическая механика. М.: Иностр. литература, 1961.
- Спасский Б. И.. История физики. М., «Высшая школа», 1977.
- Кокарев С. С. Три лекции о законах Ньютона. Ярославль. Сб. трудов РНОЦ Логос, вып. 1, 45-72, 2006.
Ссылки новых исследований:
- Masreliez C. J., Motion, Inertia and Special Relativity — a Novel Perspective, Physica Scripta (2006).
- Masreliez C. J., On the origin of inertial force, Apeiron (2006).
- Masreliez, C J; Dynamic incremental scale transition with application to physics and cosmology, Physica Scripta (2007).
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 31 октября 2016;
проверки требуют 26 правок.
Инертность — свойство по значению прил. инертный — быть в состоянии покоя, бездеятельности, пассивности, вялости.
Химия[править | править код]
В химии инертными называются вещества, не являющихся химически активными.
Благородные газы были ранее известны как инертные газы из-за предполагаемого отсутствия участия в каких-либо химических реакциях. Причина этого заключается в том, что их крайняя электронная оболочка (валентная оболочка) полностью заполнена, так, что они имеют незначительную тенденцию к приобретению или потере электрона.[1] В настоящее время известно, что эти газы реагируют с образованием химических соединений, например, тетрафторида ксенона. Поэтому они были переименованы в благородные газы. Тем не менее для проведения таких реакций требуется большое количество энергии, как правило подводимой в виде тепла, давления, или излучения, а также присутствие катализаторов. Полученные соединения инертных газов часто неустойчивы. Инертные среды, состоящие из газов, таких как аргон или гелий широко используются в химических реакционных камерах и контейнерах для хранения реагентов.
Термин инертный также может быть применён в относительном смысле, как не реакционно-способный. Например, молекулярный азот инертен в обычных условиях, существующих в двухатомных молекулах, N2. Наличие сильной тройной ковалентной связи в N2 молекулах делает его не реакционно-способным в нормальных условиях. Тем не менее, азот реагирует со щелочным металлом литием, образуя нитрид лития (Li3N) даже в обычных условиях. При высоких давлениях и температурах и с нужным катализатором, азот становится более реактивным. Процесс Габера использует такие условия, для производства аммиака из азота воздуха. Инертная среда из азота широко используется для хранения чувствительных к кислороду или водно-чувствительных веществ, чтобы предотвратить нежелательные реакции этих веществ с кислородом или водой.
Физика[править | править код]
Инертность — свойство тела в большей или меньшей степени препятствовать изменению своей скорости относительно инерциальной системы отсчёта при воздействии на него внешних сил.[2] Упоминается в русскоязычной литературе, наряду с Инерцией, как синоним, но дается несколько различное определение. Ине́ртность (от лат. inertia — бездеятельность, косность.) — свойство тел оставаться в некоторых системах отсчёта в состоянии покоя или равномерного прямолинейного движения в отсутствие или при взаимной компенсации внешних воздействий.[3] Мерой инертности в поступательном движении является масса тела[4]. Мерой инертности во вращательном движении является момент инерции[5].
Пестициды[править | править код]
Федеральный закон США о Инсектицидах, Фунгицидах и Родентицидах (англ.)русск. делит ингредиенты в пестицидах на две группы: активные и инертные. Химически инертные, в этом контексте, это такие, которые не оказывают токсического влияния на определённые виды, для защиты которых предназначены пестициды, но это не исключает, что они всё ещё могут иметь биологическую активность на другие виды, в том числе, могут быть токсичны для человека. В частности, растворители, пропелленты, консерванты, кроме прочего, считаются инертными ингредиентами (англ.)русск.[6] в пестицидах.[7]
Начиная с 1997 года, Агентство по охране окружающей среды США рекомендовало производителям пестицидов маркировать неактивные ингредиенты как «прочие ингредиенты», а не «инертные», чтобы предотвратить дезинформацию общественности.[7].
В русскоязычной литературе термин инертность используется в работах по пестицидам
[8], биотехнологиям[9], а также в официальных инструкциях препаратов, например «Агропол».
Алгебра[править | править код]
В алгебре, простой идеал дедекиндова кольца называют инертным, если он по-прежнему простой, при рассмотрении в расширении поля. Такой простой идеал, возможно, вместо разбиения простых идеалов на расширения Галуа (англ.)русск. имеет в результате другие простые идеалы, но, будучи инертным, остается практически неизменным.[10][11]
Боеприпасы[править | править код]
В области оружия и взрывчатых веществ, инертный боеприпас — такой, в котором все энергетические материалы, такие как огнепроводный шнур, капсюль, и разрывные или зажигательные материалы в них были сняты или иным образом обезврежены. Инертные врывно-тупо-режущие боеприпасы используются в военной и военно-морской подготовке и используются для показа в музеях. См. также военный муляж (англ.)русск.. Как правило, американские и натовские инертные боеприпасы окрашены полностью в светло-голубой цвет, и/или на видных местах есть слово «INERT» нанесённое по трафарету. В российской армии такие боеприпасы маркируются белой полосой и/или надписью «ИНЕРТНО» или «ИНЕРТ».[12] Регламентируются в Европейском соглашении о международной дорожной перевозке опасных грузов[13]
Ссылки[править | править код]
- ↑ Некрасов Б.В. Основы общей химии. — М.: Рипол Классик, 1965. — Т. 1. — 656 с. — ISBN 5458424085, 9785458424080.
- ↑ Инертность // Физическая энциклопедия (в 5 томах) / Под редакцией акад. А. М. Прохорова. — М.: Советская Энциклопедия, 1990. — Т. 2. — ISBN 5-85270-034-7.
- ↑ Инерция // Физическая энциклопедия (в 5 томах) / Под редакцией акад. А. М. Прохорова. — М.: Советская Энциклопедия, 1990. — Т. 2. — ISBN 5-85270-034-7.
- ↑ Инертность // Казахстан. Национальная энциклопедия. — Алматы: Қазақ энциклопедиясы, 2005. — Т. II. — ISBN 9965-9746-3-2.
- ↑ Момент инерции // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
- ↑ EPA (2010), Inert Ingredients Eligible for FIFRA 25(b) Pesticide Products Last Updated December 20, 2010, Office of prevention, pesticides and toxic substances
- ↑ 1 2 Inert ingredients in pesticide products. US Environmental Protection Agency, Office of Pesticide Programs.
- ↑ к.б.н. Семенова А.Г.; к.б.н. Свирина Н.В. Современные препаративные формы пестицидов / УДК 632.95. — Санкт-Петербург: Санкт-Петербургский Государственный Аграрный Университет, 2010. — 15 с.
- ↑ Хиггинс И., Бест Д., Джонс Дж. Биотехнология. Принципы и применение / пер. с англ. д-ра биол. н. Антонова А.С., под ред. акад. Баева А.А.. — М.: Мир (издательство), 1988. — 479 с. — ISBN 5-03-000058-5 0-623-01029-0.
- ↑ Ленг С. Origins and early evolution of predation // Алгебраические числа, пер. с англ.. — М.: Мир, 1966. — 230 с.
- ↑ Вейль Г. Алгебраическая теория чисел, пер. с англ.. — М.: Гос. изд. ин.лит., 1947. — 226 с. — ISBN 978-5-354-01363-0.
- ↑ Веремеев Ю. Маркировка инженерных боеприпасов Советской Армии // Анатомия армии. — М.: Эксмо, Алгоритм, 2010. — Т. Инженерные войска. — 292 с. — ISBN 978-5-699-46005-2.
- ↑ Организация Объединённых Наций. Европейское соглашение о международной дорожной перевозке опасных грузов. — Нью-Йорк и Женева: United Nations, 2010. — 689 с. — ISBN 978-92-1-439042-8.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 27 января 2019;
проверки требуют 5 правок.
Моме́нт ине́рции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения в Международной системе единиц (СИ): кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от типа базового множества до которого отсчитываются расстояния от элементарных масс.
Осевой момент инерции[править | править код]
Осевые моменты инерции некоторых тел
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси[1]:
где:
- mi — масса i-й точки,
- ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
где:
dm = ρ dV — масса малого элемента объёма тела dV,
ρ — плотность,
r — расстояние от элемента dV до оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
Теорема Гюйгенса — Штейнера[править | править код]
Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Гюйгенса — Штейнера, момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями[1]:
где m — полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
Осевые моменты инерции некоторых тел[править | править код]
Вывод формул[править | править код]
Тонкостенный цилиндр (кольцо, обруч)
Вывод формулы
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобьём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
Толстостенный цилиндр (кольцо, обруч)
Вывод формулы
Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R1, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит
Момент инерции толстого кольца найдём как интеграл
Поскольку объём и масса кольца равны
получаем окончательную формулу для момента инерции кольца
Однородный диск (сплошной цилиндр)
Вывод формулы
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
Сплошной конус
Вывод формулы
Разобьём конус на тонкие диски толщиной dh, перпендикулярные оси конуса. Радиус такого диска равен
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска.
Масса и момент инерции такого диска составят
Интегрируя, получим
Сплошной однородный шар
Вывод формулы
Разобьём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
Масса и момент инерции такого диска составят
Момент инерции шара найдём интегрированием:
Тонкостенная сфера
Вывод формулы
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.
Тонкий стержень (ось проходит через центр)
Вывод формулы
Разобьём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
Интегрируя, получим
Тонкий стержень (ось проходит через конец)
Вывод формулы
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l⁄2. По теореме Штейнера новый момент инерции будет равен
Безразмерные моменты инерции планет и их спутников[2][3][4]
Безразмерные моменты инерции планет и спутников[править | править код]
Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr2). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение доплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра[5][6].
Центробежный момент инерции[править | править код]
Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины[1][7]:
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.
Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции данного тела[7].
Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции[7].
Геометрические моменты инерции[править | править код]
Геометрический момент инерции объёма относительно оси — геометрическая характеристика тела, выражаемая формулой[8]:
где, как и ранее r — расстояние от элемента dV до оси a.
Размерность JVa — длина в пятой степени (), соответственно единица измерения СИ — м5.
Геометрический момент инерции площади относительно оси — геометрическая характеристика тела, выражаемая формулой[8]:
где интегрирование выполняется по поверхности S, а dS — элемент этой поверхности.
Размерность JSa — длина в четвёртой степени (), соответственно единица измерения СИ — м4. В строительных расчетах, литературе и сортаментах металлопроката часто указывается в см4.
Через геометрический момент инерции площади выражается момент сопротивления сечения:
Здесь rmax — максимальное расстояние от поверхности до оси.
Момент инерции относительно плоскости[править | править код]
Моментом инерции твёрдого тела относительно некоторой плоскости называют скалярную величину, равную сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до рассматриваемой плоскости[9].
Если через произвольную точку провести координатные оси , то моменты инерции относительно координатных плоскостей , и будут выражаться формулами:
В случае сплошного тела суммирование заменяется интегрированием.
Центральный момент инерции[править | править код]
Центральный момент инерции (момент инерции относительно точки O, момент инерции относительно полюса, полярный момент инерции) — это величина, определяемая выражением[9]:
где:
Центральный момент инерции можно выразить через главные осевые моменты инерции, а также через моменты инерции относительно плоскостей[9]:
Тензор инерции и эллипсоид инерции[править | править код]
Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором , можно представить в виде квадратичной (билинейной) формы:
(1)
где — тензор инерции. Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:
Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :
где — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:
откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на
и произведя замены:
получаем канонический вид уравнения эллипсоида в координатах :
Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:
См. также[править | править код]
Комментарии[править | править код]
- ↑ В правильности использования знака «+» в этой формуле можно убедиться, если сравнить моменты инерции полого толстостенного и сплошного цилиндров с одинаковыми массами. Действительно, у первого из этих цилиндров масса в среднем сосредоточена дальше от оси, чем у второго, поэтому и момент инерции этого цилиндра должен быть больше, чем у сплошного. Именно такое соотношение моментов инерции и обеспечивает знак «+». С другой стороны, в пределе при стремлении r1 к r2 формула для полого толстостенного цилиндра должна приобрести тот же вид, что и формула для полого тонкостенного цилиндра. Очевидно, что такой переход происходит только при использовании формулы со знаком «+».
Примечания[править | править код]
Литература[править | править код]
- Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
- Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997.
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
- Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с.
- Беляев Н. М. Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.
Ссылки[править | править код]
- Определение момента инерции тел простой формы.
