Какое свойство степени существует
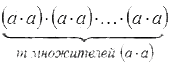
Ранее мы уже говорили о том, что такое степень числа. Она имеет определенные свойства, полезные в решении задач: именно их и все возможные показатели степени мы разберем в этой статье. Также мы наглядно покажем на примерах, как их можно доказать и правильно применить на практике.
Свойства степени с натуральным показателем
Вспомним уже сформулированное нами ранее понятие степени с натуральным показателем: это произведение n-ного количества множителей, каждый из которых равен а. Также нам понадобится вспомнить, как правильно умножать действительные числа. Все это поможет нам сформулировать для степени с натуральным показателем следующие свойства:
Определение 1
1. Главное свойство степени: am·an=am+n
Можно обобщить до: an1·an2·…·ank=an1+n2+…+nk.
2. Свойство частного для степеней, имеющих одинаковые основания: am:an=am−n
3. Свойство степени произведения: (a·b)n=an·bn
Равенство можно расширить до: (a1·a2·…·ak)n=a1n·a2n·…·akn
4. Свойство частного в натуральной степени: (a:b)n=an:bn
5. Возводим степень в степень: (am)n=am·n,
Можно обобщить до:(((an1)n2)…)nk=an1·n2·…·nk
6. Сравниваем степень с нулем:
- если a>0, то при любом натуральном n, an будет больше нуля;
- при a, равном 0, an также будет равна нулю;
- при a<0 и таком показателе степени, который будет четным числом 2·m, a2·m будет больше нуля;
- при a <0 и таком показателе степени, который будет нечетным числом 2·m−1, a2·m−1 будет меньше нуля.
7. Равенство an<bn будет справедливо для любого натурального n при условии, что a и b больше нуля и не равны друг другу.
8. Неравенство am>an будет верным при условии, что m и n – натуральные числа, m больше n и а больше нуля и не меньше единицы.
В итоге мы получили несколько равенств; если соблюсти все условия, указанные выше, то они будут тождественными. Для каждого из равенств, например, для основного свойства, можно поменять местами правую и левую часть: am·an=am+n — то же самое, что и am+n=am·an. В таком виде оно часто используется при упрощении выражений.
Далее мы разберем каждое свойство подробно и попробуем привести доказательства.
1. Начнем с основного свойства степени: равенство am·an=am+n будет верным при любых натуральных m и n и действительном a. Как доказать это утверждение?
Основное определение степеней с натуральными показателями позволит нам преобразовать равенство в произведение множителей. Мы получим запись такого вида:
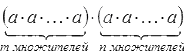
Это можно сократить до 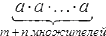 (вспомним основные свойства умножения). В итоге мы получили степень числа a с натуральным показателем m+n. Таким образом, am+n, значит, основное свойство степени доказано.
(вспомним основные свойства умножения). В итоге мы получили степень числа a с натуральным показателем m+n. Таким образом, am+n, значит, основное свойство степени доказано.
Разберем конкретный пример, подтверждающий это.
Пример 1
Итак, у нас есть две степени с основанием 2. Их натуральные показатели — 2 и 3 соответственно. У нас получилось равенство: 22·23=22+3=25 Вычислим значения, чтобы проверить верность этого равенства.
Выполним необходимые математические действия: 22·23=(2·2)·(2·2·2)=4·8=32 и 25=2·2·2·2·2=32
В итоге у нас вышло: 22·23=25. Свойство доказано.
В силу свойств умножения мы можем выполнить обобщение свойства, сформулировав его в виде трех и большего числа степеней, у которых показатели являются натуральными числами, а основания одинаковы. Если обозначить количество натуральных чисел n1, n2 и др. буквой k, мы получим верное равенство:
an1·an2·…·ank=an1+n2+…+nk.
Пример 2
Пример с конкретными числами (легко посчитать самостоятельно): (2,1)3·(2,1)3·(2,1)4·(2,1)7=(2,1)3+3+4+7=(2,1)17.
2. Далее нам необходимо доказать следующее свойство, которое называется свойством частного и присуще степеням с одинаковыми основаниями: это равенство am:an=am−n, которое справедливо при любых натуральным m и n (причем m больше n) ) и любом отличном от нуля действительном a.
Для начала поясним, каков именно смысл условий, которые упомянуты в формулировке. Если мы возьмем a, равное нулю, то в итоге у нас получится деление на нуль, чего делать нельзя (ведь 0n=0). Условие, чтобы число m обязательно было больше n, нужно для того, чтобы мы могли удержаться в рамках натуральных показателей степени: вычтя n из m, мы получим натуральное число. Если условие не будет соблюдено, у нас получится отрицательное число или ноль, и опять же мы выйдем за пределы изучения степеней с натуральными показателями.
Теперь мы можем перейти к доказательству. Из ранее изученного вспомним основные свойства дробей и сформулируем равенство так:
am−n·an=a(m−n)+n=am
Из него можно вывести: am−n·an=am
Вспомним про связь деления и умножения. Из него следует, что am−n– частное степеней am и an. Это и есть доказательство второго свойства степени.
Пример 3
Подставим конкретные числа для наглядности в показатели, а основание степени обозначим π: π5:π2=π5−3=π3
3. Следующим мы разберем свойство степени произведения: (a·b)n=an·bn при любых действительных a и b и натуральном n.
Согласно базовому определению степени с натуральным показателем мы можем переформулировать равенство так:
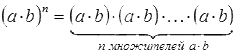
Вспомнив свойства умножения, запишем: 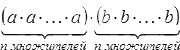 . Это значит то же самое, что и an·bn.
. Это значит то же самое, что и an·bn.
Пример 4
23·-4254=234·-4254
Если множителей у нас три и больше, то это свойство также распространяется и на этот случай. Введем для числа множителей обозначение k и запишем:
(a1·a2·…·ak)n=a1n·a2n·…·akn
Пример 5
С конкретными числами получим следующее верное равенство: (2·(-2,3)·a)7=27·(-2,3)7·a
4. После этого мы попробуем доказать свойство частного: (a:b)n=an:bn при любых действительных a и b, если b не равно 0, а n – натуральное число.
Для доказательства можно использовать предыдущее свойство степени. Если (a:b)n·bn=((a:b)·b)n=an , а (a:b)n·bn=an, то из этого выходит, что (a:b)n есть частное от деления an на bn.
Пример 6
Подсчитаем пример: 312:-0.53=3123:(-0,5)3
5. Далее мы поговорим о свойстве возведения степени в степень: (am)n=am·n для любого действительного a и любых натуральных n и m.
Пример 7
Начнем сразу с примера: (52)3=52·3=56
А теперь сформулируем цепочку равенств, которая докажет нам верность равенства: 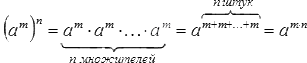
Если у нас в примере есть степени степеней, то это свойство справедливо для них также. Если у нас есть любые натуральные числа p, q, r, s, то верно будет:
apqys=ap·q·y·s
Пример 8
Добавим конкретики: (((5,2)3)2)5=(5,2)3·2·5=(5,2)30
6. Еще одно свойство степеней с натуральным показателем, которое нам нужно доказать, – свойство сравнения.
Для начала сравним степень с нулем. Почему an>0 при условии, что а больше 0?
Если умножить одно положительное число на другое, то мы получим также положительное число. Зная этот факт, мы можем сказать, что от числа множителей это не зависит – результат умножения любого числа положительных чисел есть число положительное. А что же такое степень, как не результат умножения чисел? Тогда для любой степени an с положительным основанием и натуральным показателем это будет верно.
Пример 9
35>0, (0,00201)2>0 и 3491351>0
Также очевидно, что степень с основанием, равным нулю, сама есть ноль. В какую бы степень мы не возводили ноль, он останется им.
Пример 10
03=0 и 0762=0
Если основание степени – отрицательное число, тот тут доказательство немного сложнее, поскольку важным становится понятие четности/нечетности показателя. Возьмем для начала случай, когда показатель степени четный, и обозначим его 2·m, где m – натуральное число.
Тогда:
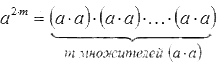
Вспомним, как правильно умножать отрицательные числа: произведение a·a равно произведению модулей, а, следовательно, оно будет положительным числом. Тогда 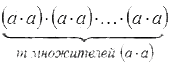 и степень a2·m также положительны.
и степень a2·m также положительны.
Пример 11
Например, (−6)4>0, (−2,2)12>0 и -296>0
А если показатель степени с отрицательным основанием – нечетное число? Обозначим его 2·m−1.
Тогда 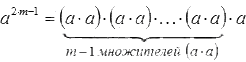
Все произведения a·a, согласно свойствам умножения, положительны, их произведение тоже. Но если мы его умножим на единственное оставшееся число a, то конечный результат будет отрицателен.
Тогда получим: (−5)3<0, (−0,003)17<0 и -111029<0
7. Далее разберем следующее свойство, формулировка которого такова: из двух степеней, имеющих одинаковый натуральный показатель, больше та, основание которой больше (и наоборот).
Как это доказать?
an<bn– неравенство, представляющее собой произведение левых и правых частей nверных неравенств a<b. Вспомним основные свойства неравенств справедливо и an<bn.
Пример 12
Например, верны неравенства: 37<(2,2)7 и 3511124>(0,75)124
8. Нам осталось доказать последнее свойство: если у нас есть две степени, основания которых одинаковы и положительны, а показатели являются натуральными числами, то та из них больше, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше.
Докажем эти утверждения.
Для начала нам нужно убедиться, что am<an при условии, что m больше, чем n, и а больше 0, но меньше 1.Теперь сравним с нулем разность am−an
Вынесем an за скобки, после чего наша разность примет вид an·(am−n−1). Ее результат будет отрицателен (поскольку отрицателен результат умножения положительного числа на отрицательное). Ведь согласно начальным условиям, m−n>0, тогда am−n−1–отрицательно, а первый множитель положителен, как и любая натуральная степень с положительным основанием.
У нас вышло, что am−an<0 и am<an. Свойство доказано.
Осталось привести доказательство второй части утверждения, сформулированного выше: am>a справедливо при m>n и a>1. Укажем разность и вынесем an за скобки: (am−n−1).Степень an при а, большем единицы, даст положительный результат; а сама разность также окажется положительна в силу изначальных условий, и при a>1 степень am−n больше единицы. Выходит, am−an>0 и am>an, что нам и требовалось доказать.
Пример 13
Пример с конкретными числами: 37>32
Основные свойства степеней с целыми показателями
Для степеней с целыми положительными показателями свойства будут аналогичны, потому что целые положительные числа являются натуральными, а значит, все равенства, доказанные выше, справедливы и для них. Также они подходят и для случаев, когда показатели отрицательны или равны нулю (при условии, что само основание степени ненулевое).
Таким образом, свойства степеней такие же для любых оснований a и b (при условии, что эти числа действительны и не равны 0) и любых показателей m и n (при условии, что они являются целыми числами). Запишем их кратко в виде формул:
Определение 2
1. am·an=am+n
2. am:an=am−n
3. (a·b)n=an·bn
4. (a:b)n=an:bn
5. (am)n=am·n
6. an<bn и a−n>b−n при условии целого положительного n, положительных a и b, a<b
7. am<an, при условии целых m и n, m>n и 0<a<1, при a>1 am>an.
Если основание степени равно нулю, то записи am и an имеют смысл только лишь в случае натуральных и положительных m и n. В итоге получим, что формулировки выше подходят и для случаев со степенью с нулевым основанием, если соблюдаются все остальные условия.
Доказательства этих свойств в данном случае несложные. Нам потребуется вспомнить, что такое степень с натуральным и целым показателем, а также свойства действий с действительными числами.
Разберем свойство степени в степени и докажем, что оно верно и для целых положительных, и для целых неположительных чисел. Начнем с доказательства равенств (ap)q=ap·q, (a−p)q=a(−p)·q, (ap)−q=ap·(−q) и (a−p)−q=a(−p)·(−q)
Условия: p=0 или натуральное число; q– аналогично.
Если значения p и q больше 0, то у нас получится (ap)q=ap·q. Схожее равенство мы уже доказывали раньше. Если p=0, то:
(a0)q=1q=1 a0·q=a0=1
Следовательно, (a0)q=a0·q
Для q=0 все точно так же:
(ap)0=1 ap·0=a0=1
Итог: (ap)0=ap·0.
Если же оба показателя нулевые, то (a0)0=10=1 и a0·0=a0=1, значит, (a0)0=a0·0.
Далее разберем равенство (a−p)q=a(−p)·q. Согласно определению степени с целым отрицательным показателем имеем a-p=1ap, значит, (a-p)q=1apq.
Вспомним доказанное выше свойство частного в степени и запишем:
1apq=1qapq
Если 1p=1·1·…·1=1 иapq=ap·q, то 1qapq=1ap·q
Эту запись мы можем преобразовать в силу основных правил умножения в a(−p)·q.
Так же: ap-q=1(ap)q=1ap·q=a-(p·q)=ap·(-q).
И (a-p)-q=1ap-q=(ap)q=ap·q=a(-p)·(-q)
Остальные свойства степени можно доказать аналогичным образом, преобразовав имеющиеся неравенства. Подробно останавливаться мы на этом не будем, укажем только сложные моменты.
Доказательство предпоследнего свойства: вспомним, a−n>b−n верно для любых целых отрицательных значений nи любых положительных a и b при условии, что a меньше b.
Тогда неравенство можно преобразовать следующим образом:
1an>1bn
Запишем правую и левую части в виде разности и выполним необходимые преобразования:
1an-1bn=bn-anan·bn
Вспомним, что в условии a меньше b, тогда, согласно определению степени с натуральным показателем: — an<bn, в итоге: bn−an>0.
an·bn в итоге дает положительное число, поскольку его множители положительны. В итоге мы имеем дробь bn-anan·bn, которая в итоге также дает положительный результат. Отсюда 1an>1bn откуда a−n>b−n, что нам и нужно было доказать.
Последнее свойство степеней с целыми показателями доказывается аналогично свойству степеней с показателями натуральными.
Основные свойства степеней с рациональными показателями
В предыдущих статьях мы разбирали, что такое степень с рациональным (дробным) показателем. Их свойства такие же, что и у степеней с целыми показателями. Запишем:
Определение 3
1. am1n1·am2n2=am1n1+m2n2 при a>0, а если m1n1>0 и m2n2>0, то при a≥0 ( свойство произведения степеней с одинаковыми основаниями).
2.am1n1:bm2n2=am1n1-m2n2 , если a>0 (свойство частного).
3. a·bmn=amn·bmn при a>0 и b>0, а если m1n1>0 и m2n2>0, то при a≥0 и (или) b≥0 (свойство произведения в дробной степени).
4. a:bmn=amn:bmn при a>0 и b>0, а если mn>0, то при a≥0 и b>0 (свойство частного в дробной степени).
5. am1n1m2n2=am1n1·m2n2 при a>0, а если m1n1>0 и m2n2>0, то при a≥0 (свойство степени в степени).
6. ap<bp при условии любых положительных a и b, a<b и рациональном p при p>0; если p<0 — ap>bp (свойство сравнения степеней с равными рациональными показателями).
7. ap<aq при условии рациональных чисел p и q, p>q при 0<a<1; если a>0 – ap>aq
Для доказательства указанных положений нам понадобится вспомнить, что такое степень с дробным показателем, каковы свойства арифметического корня n-ной степени и каковы свойства степени с целыми показателем. Разберем каждое свойство.
Согласно тому, что из себя представляет степень с дробным показателем, получим:
am1n1=am1n1 и am2n2=am2n2, следовательно, am1n1·am2n2=am1n1·am2n2
Свойства корня позволят нам вывести равенства:
am1·m2n1·n2·am2·m1n2·n1=am1·n2·am2·n1n1·n2
Из этого получаем: am1·n2·am2·n1n1·n2=am1·n2+m2·n1n1·n2
Преобразуем:
am1·n2·am2·n1n1·n2=am1·n2+m2·n1n1·n2
Показатель степени можно записать в виде:
m1·n2+m2·n1n1·n2=m1·n2n1·n2+m2·n1n1·n2=m1n1+m2n2
Это и есть доказательство. Второе свойство доказывается абсолютно так же. Запишем цепочку равенств:
am1n1: am2n2=am1n1: am2n2=am1·n2:am2·n1n1·n2==am1·n2-m2·n1n1·n2=am1·n2-m2·n1n1·n2=am1·n2n1·n2-m2·n1n1·n2=am1n1-m2n2
Доказательства остальных равенств:
a·bmn=(a·b)mn=am·bmn=amn·bmn=amn·bmn;(a:b)mn=(a:b)mn=am:bmn==amn:bmn=amn:bmn;am1n1m2n2=am1n1m2n2=am1n1m2n2==am1m2n1n2=am1·m2n1n2==am1·m2n2·n1=am1·m2n2·n1=am1n1·m2n2
Следующее свойство: докажем, что для любых значений a и b больше 0, если а меньше b, будет выполняться ap<bp, а для p больше 0 — ap>bp
Представим рациональное число p как mn. При этом m–целое число, n–натуральное. Тогда условия p<0 и p>0 будут распространяться на m<0 и m>0. При m>0 и a<b имеем (согласно свойству степени с целым положительным показателем), что должно выполняться неравенство am<bm.
Используем свойство корней и выведем: amn<bmn
Учитывая положительность значений a и b, перепишем неравенство как amn<bmn. Оно эквивалентно ap<bp.
Таким же образом при m<0 имеем a am>bm, получаем amn>bmn значит, amn>bmn и ap>bp.
Нам осталось привести доказательство последнего свойства. Докажем, что для рациональных чисел p и q, p>q при 0<a<1 ap<aq, а при a>0 будет верно ap>aq.
Рациональные числа p и q можно привести к общему знаменателю и получить дроби m1n и m2n
Здесь m1 и m2 – целые числа, а n – натуральное. Если p>q, то m1>m2 (учитывая правило сравнения дробей). Тогда при 0<a<1 будет верно am1<am2, а при a>1 – неравенство a1m>a2m.
Их можно переписать в следующем виде:
am1n<am2nam1n>am2n
Тогда можно сделать преобразования и получить в итоге:
am1n<am2nam1n>am2n
Подводим итог: при p>q и 0<a<1 верно ap<aq, а при a>0– ap>aq.
Основные свойства степеней с иррациональными показателями
На такую степень можно распространить все описанные выше свойства, которыми обладает степень с рациональными показателями. Это следует из самого ее определения, которое мы давали в одной из предыдущих статей. Сформулируем кратко эти свойства (условия: a>0, b>0, показатели p и q– иррациональные числа):
Определение 4
1. ap·aq=ap+q
2. ap:aq=ap−q
3. (a·b)p=ap·bp
4. (a:b)p=ap:bp
5. (ap)q=ap·q
6. ap<bp верно при любых положительных a и b, если a<b и p – иррациональное число больше 0; если p меньше 0, то ap>bp
7. ap<aq верно, если p и q– иррациональные числа, p<q, 0<a<1; если a>0, то ap>aq.
Таким образом, все степени, показатели которых p и q являются действительными числами, при условии a>0 обладают теми же свойствами.
Возведе́ние в сте́пень — арифметическая операция, первоначально определяемая как результат многократного умножения числа на себя. Степень с основанием и натуральным показателем обозначается как
где — количество множителей (умножаемых чисел)[1][К 1].
Например,
В языках программирования, где написание невозможно, применяются альтернативные обозначения[⇨].
Возведение в степень может быть определено также для отрицательных[⇨], рациональных[⇨], вещественных[⇨] и комплексных[⇨] степеней[1].
Извлечение корня — одна из операций, обратных возведению в степень, она по известным значениям степени и показателя находит неизвестное основание . Вторая обратная операция — логарифмирование, она по известным значениям степени и основания находит неизвестный показатель . Задача нахождения числа по известному его логарифму (потенцирование, антилогарифм) решается с помощью операции возведения в степень[⇨]).
Существует алгоритм быстрого возведения в степень, выполняющий возведение в степень за меньшее, чем в определении, число умножений.
Употребление в устной речи[править | править код]
Запись обычно читается как «a в -й степени» или «a в степени n». Например, читается как «десять в четвёртой степени», читается как «десять в степени три вторых (или: полтора)».
Для второй и третьей степени существуют специальные названия: возведение в квадрат и в куб соответственно. Так, например, читается как «десять в квадрате», читается как «десять в кубе». Такая терминология возникла из древнегреческой математики. Древние греки формулировали алгебраические конструкции на языке геометрической алгебры. В частности, вместо употребления слова «умножение» они говорили о площади прямоугольника или об объёме параллелепипеда: вместо , древние греки говорили «квадрат на отрезке a», «куб на a». По этой причине четвёртую степень и выше древние греки избегали[2].
Свойства[править | править код]
Основные свойства[править | править код]
Все приведенные ниже основные свойства возведения в степень выполняются для натуральных, целых, рациональных и вещественных чисел[3]. Для комплексных чисел, в силу многозначности комплексной операции, они выполняются только в случае натурального показателя степени[⇨].
Запись не обладает свойством ассоциативности (сочетательности), то есть, в общем случае, Например, , а . В математике принято считать запись равнозначной , а вместо можно писать просто , пользуясь предыдущим свойством. Впрочем, некоторые языки программирования не придерживаются этого соглашения.
Возведение в степень не обладает свойством коммутативности (переместительности): вообще говоря, , например, , но
Таблица натуральных степеней небольших чисел[править | править код]
| n | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
|---|---|---|---|---|---|---|---|---|---|
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3 | 9 | 27 | 81 | 243 | 729 | 2 187 | 6 561 | 19 683 | 59 049 |
| 4 | 16 | 64 | 256 | 1024 | 4 096 | 16 384 | 65 536 | 262 144 | 1 048 576 |
| 5 | 25 | 125 | 625 | 3125 | 15 625 | 78 125 | 390 625 | 1 953 125 | 9 765 625 |
| 6 | 36 | 216 | 1296 | 7 776 | 46 656 | 279 936 | 1 679 616 | 10 077 696 | 60 466 176 |
| 7 | 49 | 343 | 2401 | 16 807 | 117 649 | 823 543 | 5 764 801 | 40 353 607 | 282 475 249 |
| 8 | 64 | 512 | 4096 | 32 768 | 262 144 | 2 097 152 | 16 777 216 | 134 217 728 | 1 073 741 824 |
| 9 | 81 | 729 | 6561 | 59 049 | 531 441 | 4 782 969 | 43 046 721 | 387 420 489 | 3 486 784 401 |
| 10 | 100 | 1000 | 10 000 | 100 000 | 1 000 000 | 10 000 000 | 100 000 000 | 1 000 000 000 | 10 000 000 000 |
Расширения[править | править код]
Целая степень[править | править код]
Операция обобщается на произвольные целые числа, включая отрицательные и ноль[4]::
Результат не определён при и .
Рациональная степень[править | править код]
Возведение в рациональную степени где — целое число, а — натуральное, определяется следующим образом[4]:
.
Результат не определён при и Для отрицательных в случае нечётного и чётного в результате вычисления степени получаются комплексные числа.
Следствие: Таким образом, понятие рациональной степени объединяет возведение в целочисленную степень и извлечение корня в единую операцию.
Вещественная степень[править | править код]
Если — вещественные числа, причём — иррациональное число, возможно определить следующим образом: поскольку любое вещественное число можно приблизить, сверху и снизу, двумя рациональными числами, то есть можно подобрать для рациональный интервал с любой степенью точности, то общая часть всех соответствующих интервалов состоит из одной точки, которая и принимается за .
Полезные формулы:
Последние две формулы используют для возведения положительных чисел в произвольную степень на электронных калькуляторах (включая компьютерные программы), не имеющих встроенной функции , и для приближённого возведения в нецелую степень или для целочисленного возведения в степень, когда числа слишком велики для того, чтобы записать результат полностью.
Комплексная степень[править | править код]
Возведение комплексного числа в натуральную степень выполняется обычным умножением, и результат однозначен (см. формулу Муавра). Основой для более общего определения комплексной степени служит экспонента , где — число Эйлера, — произвольное комплексное число[5].
Определим комплексную экспоненту с помощью такого же ряда, как и вещественную:
Этот ряд абсолютно сходится для любого комплексного поэтому его члены можно как угодно перегруппировывать. В частности, отделим от него часть для :
В скобках получились известные из вещественного анализа ряды для косинуса и синуса, и мы получили формулу Эйлера:
Общий случай , где — комплексные числа, определяется через представление в показательной форме: согласно определяющей формуле[5]:
Здесь — комплексный логарифм, — его главное значение.
При этом комплексный логарифм — многозначная функция, так что, вообще говоря, комплексная степень определена неоднозначно[5]. Неучёт этого обстоятельства может привести к ошибкам. Пример: возведём известное тождество в степень Слева получится справа, очевидно, 1. В итоге: что, как легко проверить, неверно. Причина ошибки: возведение в степень даёт и слева, и справа бесконечное множество значений (при разных ), поэтому правило здесь неприменимо. Аккуратное применение формул определения комплексной степени даёт слева и справа отсюда видно, что корень ошибки — путаница значений этого выражения при и при
Потенцирование и антилогарифм[править | править код]
Потенцирование (от нем. potenzieren[К 2]) — нахождение числа по известному значению его логарифма, то есть решение уравнения . Из определения логарифма вытекает, что , таким образом, возведение в степень может быть названо другими словами «потенцированием по основанию ».
Антилогарифм — результат потенцирования, то есть нахождения числа по известному значению его логарифма[6]. Как самостоятельное понятие используется в логарифмических таблицах, логарифмических линейках, микрокалькуляторах.
Согласно сказанному выше, антилогарифм по основанию для числа равен :
Степень как функция[править | править код]
Разновидности[править | править код]
Поскольку в выражении используются два символа ( и ), то его можно рассматривать как одну из трёх функций.
Ноль в степени ноль[править | править код]
Выражение (ноль в нулевой степени) многие учебники считают неопределённым и лишённым смысла, поскольку, как указано выше, функция в точке (0, 0) разрывна. Некоторые авторы предлагают принять соглашение о том, что это выражение равно 1. В частности, тогда разложение в ряд экспоненты:
можно записать короче:
Следует предостеречь, что соглашение чисто символическое, и оно не может использоваться ни в алгебраических, ни в аналитических преобразованиях из-за разрывности функции в этой точке.
История[править | править код]
Обозначение[править | править код]
В Европе сначала степень величины записывали словесными сокращениями (q или Q обозначало квадрат, c или C — куб, bq или qq — биквадрат, то есть 4-я степень и т. д.) или как произведение — например, изображалось как Отред записывал следующим образом: (если неизвестная всего одна, ей часто не присваивался буквенный значок)[7]. Немецкая школа коссистов для каждой степени неизвестной предлагала особый готический значок.
В XVII веке постепенно стала преобладать идея явно указывать показатель степени. Жирар (1629 год) для возведения в степень числа ставил показатель в круглых скобках перед этим числом, а если числа правее показателя не было, то это значило, что подразумевается наличие неизвестного в указанной степени[8]; например, у него означало . Варианты размещения показателя степени предлагали Пьер Эригон и шотландский математик Джеймс Юм, они записывали в виде и соответственно[9].
Современная запись показателя степени — правее и выше основания — введена Декартом в его «Геометрии» (1637), правда, только для натуральных степеней, больших 2 (возведение в квадрат ещё долгое время обозначалось по-старому, произведением). Позднее Валлис и Ньютон (1676) распространили декартову форму записи степени на отрицательные и дробные показатели, трактовка которых к этому времени уже была известна из трудов Орема, Шюке, Стевина, Жирара и самого Валлиса. К началу XVIII столетия альтернативы для записи степеней «по Декарту», как выразился Ньютон в «Универсальной арифметике», «вышли из моды» (out of fashion). Показательная функция, то есть возведение в переменную степень, появилась сначала в письмах, а потом и в трудах Лейбница (1679). Возведение в мнимую степень обосновал Эйлер (1743)[9][10].
Запись возведения в степень в языках программирования[править | править код]
С появлением компьютеров и компьютерных программ возникла проблема, состоящая в том, что в тексте компьютерных программ невозможно записать степень в «двухэтажном» виде. В связи с этим изобрели особые значки для обозначения операции возведения в степень. Первым таким значком были две звёздочки: «**», используемые в языке Фортран. В появившемся несколько позже языке Алгол использовался значок стрелки: «↑» (стрелки Кну́та). В языке Бейсик предложен символ «^» («циркумфлекс»), который приобрёл наибольшую популярность; его часто используют при написании формул и математических выражений не только в языках программирования и компьютерных системах, но и в простом тексте. Примеры:
3^2 = 9; 5^2 = 25; 2^3 = 8; 5^3 = 125.
Иногда в компьютерных системах и языках программирования значок возведения в степень имеет левую ассоциативность, в отличие от принятого в математике соглашения о правой ассоциативности возведения в степень.
То есть некоторые языки программирования (например, программа Excel) могут воспринимать запись a^b^c, как (a^b)^c, тогда как другие системы и языки (например, Haskell, Perl, Wolfram|Alpha и многие другие) обработают эту запись справа налево: a^(b^c), как это принято в математике: .
Некоторые знаки возведения в степень в языках программирования и компьютерных системах:
- x ↑ y: Алгол, некоторые диалекты Бейсика;
- x ^ y: Бейсик, J, MATLAB, R, Microsoft Excel, TeX, bc[К 3], Haskell[К 4], Lua, MathML и большинство систем компьютерной алгебры;
- x ^^ y: Haskell[К 5], D;
- x ** y: Ада, Bash, Кобол, Фортран, FoxPro, Gnuplot, OCaml, Perl, PL/I, PHP[К 6], Python, REXX, Ruby, SAS, Seed7, Tcl, ABAP, Haskell[К 7], Turing[en], VHDL, ECMAScript[К 8][К 9], AutoHotkey[К 9], JavaScript;
- x⋆y: APL.
Во многих языках программирования (например, в Java, Си и Паскале) отсутствует операция возведения в степень, и для этой цели используют стандартные функции.
Вариации и обобщения[править | править код]
Возведение в степень с натуральным показателем можно определить не только для чисел, но и для нечисловых объектов, для которых определено умножение — например, к матрицам, линейным операторам, множествам (относительно декартова произведения, см. декартова степень).
Обычно эта операция рассматривается в некотором мультипликативном моноиде (полугруппе с единицей) и определяется индуктивно[11] для любого :
Особенную ценность представляет применение возведения в степень к группам и полям, где возникает прямой аналог отрицательных степеней.
Гипероператор возведения в степень — тетрация.
Примечания[править | править код]
- ↑ 1 2 Степень // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1985. — Т. 5. — С. 221.
- ↑ Ван дер Варден. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции / Пер. с голл. И. Н. Веселовского. — М., 1959. — С. 165—167. — 456 с.
- ↑ Справочник по элементарной математике, 1978, с. 140—141.
- ↑ 1 2 Справочник по элементарной математике, 1978, с. 182—184.
- ↑ 1 2 3 Выгодский М. Я. Справочник по высшей математике. — 12-е изд.. — М.: Наука, 1977. — С. 597 (подстрочное примечание 3). — 872 с.
- ↑ Антилогарифм / Математический энциклопедический словарь, М.: Советская энциклопедия, 1988, стр. 73.
- ↑ History of Mathematical Notations, vol. 1, 2007, §290—297.
- ↑ History of Mathematical Notations, vol. 1, 2007, §164.
- ↑ 1 2 Александрова Н. В., 2008, с. 130—131.
- ↑ History of Mathematical Notations, vol. 1, 2007, §298—301, 307—309.
- ↑ David M. Bloom. Linear Algebra and Geometry (англ.). — 1979. — P. 45. — ISBN 978-0-521-29324-2.
Комментарии
- ↑ В разговорной речи иногда говорят, например, что — «a умноженное само на себя три раза», имея в виду, что берётся три множителя . Это не совсем точно и может привести к двусмысленности, так как количество операций умножения будет на одну меньше: (три множителя, но две операции умножения). Часто, когда говорят «a умноженное само на себя три раза», имеют в виду количество умножений, а не множителей, то есть См. Август Давидов. Начальная алгебра. — Типографія Э. Лисслер и Ю. Роман, 1883-01-01. — С. 6. — 534 с.. Чтобы избежать двусмысленности, можно говорить, к примеру: третья степень — это когда «число три раза входит в умножение».
- ↑ Термин впервые встречается у швейцарского математика Иоганна Рана (1659 год).
- ↑ Для целой степени.
- ↑ Для неотрицательной целой степени.
- ↑ Поддерживает отрицательные степени, в отличие от ^, реализованной только как последовательное умножение.
- ↑ Начиная с версии 5.6 (см. Руководство по PHP › Appendices › Миграция с PHP 5.5.x на PHP 5.6.x › Новые возможности).
- ↑ Для степени, представленной числом с плавающей запятой — реализовано через логарифм.
- ↑ Описан в стандарте EcmaScript 7 (ECMA-262, 7th edition), принятом в июне 2016 года.
- ↑ 1 2 В JavaScript изначально присутствует метод Math.pow(x, y).
Литература[править | править код]
- Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник. — 3-е изд. — СПб.: ЛКИ, 2008. — 248 с. — ISBN 978-5-382-00839-4.
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978. — 509 с.
- Переиздание: М.: АСТ, 2006, ISBN 5-17-009554-6, 509 стр.
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
- Степенная функция // Большая советская энциклопедия. — М.: Советская энциклопедия, 1969—1978.
- Cajori F. A History of Mathematical Notations. Vol. 1 (1929 reprint). — NY: Cosimo, Inc., 2007. — xvi + 456 p. — ISBN 978-1-60206-684-7.
Ссылки[править | править код]
- Возведение в степень: правила, примеры. Дата обращения 2 февраля 2020.
