Какое свойство силы упругости
Сила упругости
Любое тело, когда его деформируют и оказывают внешнее воздействие, сопротивляется и стремиться восстановить прежние форму и размеры. Это происходит по причине электромагнитного взаимодействия в теле на молекулярном уровне.
Деформация — изменение положения частиц тела друг относительно друга. Результат деформации — изменение межатомных расстояний и перегруппировка блоков атомов.
Определение. Что такое сила упругости?
Сила упругости — сила, возникающая при деформации в теле и стремящаяся вернуть тело в начальное состояние.
Рассмотрим простейшие деформации — растяжение и сжатие
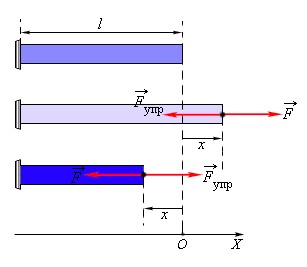
На рисунке показано, как действует сила упругости, когда мы сжимаем или растягиваем стержень.
Закон Гука
Для малых деформаций x≪ l справедлив закон Гука.
Закон Гука
Деформация, возникающая в упругом теле, пропорциональна приложенной к телу силе.
Fупр=-kx
Здесь k — коэффициент пропорциональности, называемый жесткостью. Единица измерения жесткости системе СИ Ньютон на метр. Жесткость зависит от материала тела, его формы и размеров.
Знак минус показывает, что сила упругости противодействует внешней силе и стремится вернуть тело в первоначальное состояние.
Существуют и другие формы записи закона Гука. Относительной деформацией тела называется отношение ε=xl. Напряжением в теле называется отношение σ=-FупрS. Здесь S — площадь поперечного сечения деформированного тела. Вторая формулировка закона Гука: относительная деформация пропорциональна напряжению.
ε=σE.
Здесь E — так называемый модуль Юнга, который не зависит от формы и размеров тела, а зависит только от свойств материала. Значение модуля Юнга для различных материалов широко варьируется. Например, для стали E≈2·1011 Нм2, а для резины E≈2·106 Нм2
Закон Гука можно обобщить для случая сложных деформаций. Рассмотрим деформацию изгиба стержня. При такой деформации изгиба сила упругости пропорциональна прогибу стержня.
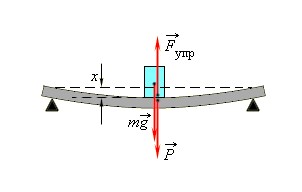
Концы стержня лежат на двух опорах, которые действуют на тело с силой N→, называемой силой нормальной реакции опоры. Почему нормальной? Потому что эта сила направлена перпендикулярно (нормально) поверхности соприкосновения.
Если стержень лежит на столе, сила нормальной реакции опоры направлена вертикально вверх, противоположно силе тяжести, которую она уравновешивает.
Вес тела — это сила, с которой оно действует на опору.
Силу упругости часто рассматривают в контексте растяжения или сжатия пружины. Это распространенный пример, который часто встречается не только в теории, но и на практике. Пружины используются для измерения величины сил. Прибор, предназначенный для этого — динамаметр.
Динамометр — пружина, растяжение которой проградуированно в единицах силы. Характерное свойство пружин заключается в том, что закон Гука для них применим при достаточно большом изменении длины.
При сжатии и растяжении пружины действует закон Гука, возникают упругие силы, пропорциональные изменению длины пружины и ее жесткости (коэффициента k).
В отличие от пружин стержни и проволоки подчиняются закону Гука в очень узких пределах. Так, при относительной дефомации больше 1% в материале возникают необратимые именения — текучесть и разрушения.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: силы в механике, сила упругости, закон Гука.
Как мы знаем, в правой части второго закона Ньютона стоит равнодействующая (то есть векторная сумма) всех сил, приложенных к телу. Теперь нам предстоит изучить силы взаимодействия тел в механике. Их три вида: сила упругости, гравитационная сила и сила трения. Начинаем с силы упругости.
Деформация.
Силы упругости возникают при деформациях тел. Деформация — это изменение формы и размеров тела. К деформациям относятся растяжение, сжатие, кручение, сдвиг и изгиб.
Деформации бывают упругими и пластическими. Упругая деформация полностью исчезает после прекращения действия вызывающих её внешних сил, так что тело полностью восстанавливает форму и размеры. Пластическая деформация сохраняется (быть может, частично) после снятия внешней нагрузки, и тело уже не возвращается к прежним размерам и форме.
Частицы тела (молекулы или атомы) взаимодействуют друг с другом силами притяжения и отталкивания, имеющими электромагнитное происхождение (это силы, действующие между ядрами и электронами соседних атомов). Силы взаимодействия зависят о расстояний между частицами. Если деформации нет, то силы притяжения компенсируются силами отталкивания. При деформации изменяются расстояния между частицами, и баланс сил взаимодействия нарушается.
Например, при растяжении стержня расстояния между его частицами увеличиваются, и начинают преобладать силы притяжения. Наоборот, при сжатии стержня расстояния между частицами уменьшаются, и начинают преобладать силы отталкивания. В любом случае возникает сила, которая направлена в сторону, противоположную деформации, и стремится восстановить первоначальную конфигурацию тела.
Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Сила упругости:
1. действует между соседними слоями деформированного тела и приложена к каждому слою;
2. действует со стороны деформированного тела на соприкасающееся с ним тело, вызывающее деформацию, и приложена в месте контакта данных тел перпендикулярно их поверхностям (типичный пример — сила реакции опоры).
Силы, возникающие при пластических деформациях, не относятся к силам упругости. Эти силы зависят не от величины деформации, а от скорости её возникновения. Изучение таких сил
выходит далеко за рамки школьной программы.
В школьной физике рассматриваются растяжения нитей и тросов, а также растяжения и сжатия пружин и стержней. Во всех этих случаях силы упругости направлены вдоль осей данных тел.
Закон Гука.
Деформация называется малой, если изменение размеров тела много меньше его первоначальных размеров. При малых деформациях зависимость силы упругости от величины деформации оказывается линейной.
Закон Гука. Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину , сила упругости даётся формулой:
(1)
где — коэффициент жёсткости пружины.
Коэффициент жёсткости зависит не только от материала пружины, но также от её формы и размеров.
Из формулы (1) следует, что график зависимости силы упругости от (малой) деформации является прямой линией (рис. 1 ):
 |
| Рис. 1. Закон Гука |
Коэффициент жёсткости — о угловой коэффициент в уравнении прямой . Поэтому справедливо равенство:
,
где — угол наклона данной прямой к оси абсцисс. Это равенство удобно использовать при экспериментальном нахождении величины .
Подчеркнём ещё раз, что закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела. Когда деформации перестают быть малыми, эта зависимость перестаёт быть линейной и приобретает более сложный вид. Соответственно, прямая линия на рис. 1 — это лишь небольшой начальный участок криволинейного графика, описывающего зависимость от при всех значениях деформации .
Модуль Юнга.
В частном случае малых деформаций стержней имеется более детальная формула, уточняющая общий вид ( 1 ) закона Гука.
Именно, если стержень длиной и площадью поперечного сечения растянуть или сжать
на величину , то для силы упругости справедлива формула:
.
Здесь — модуль Юнга материала стержня. Этот коэффициент уже не зависит от геометрических размеров стержня. Модули Юнга различных веществ приведены в справочных таблицах.
Мы используем файлы cookie, чтобы персонализировать контент, адаптировать и оценивать результативность рекламы, а также обеспечить безопасность. Перейдя на сайт, вы соглашаетесь с использованием файлов cookie.
Главная
Онлайн учебники
База репетиторов России
Тренажеры по физике
Подготовка к ЕГЭ 2017 онлайн
Глава 1. Механика
Силы в природе
1.12. Сила упругости. Закон Гука
При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.
Простейшим видом деформации являются деформации растяжения и сжатия (рис. 1.12.1).
| Рисунок 1.12.1. Деформация растяжения ( x > 0 ) и сжатия ( x < 0 ). Внешняя сила |
При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:
Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м). Коэффициент жесткости зависит от формы и размеров тела, а также от материала. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение ε = x / l называется относительной деформацией, а отношение σ = F / S = –Fупр / S, где S – площадь поперечного сечения деформированного тела, называется напряжением. Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ:
Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Модуль Юнга различных материалов меняется в широких пределах. Для стали, например, E ≈ 2·1011 Н/м2, а для резины E ≈ 2·106 Н/м2, т. е. на пять порядков меньше.
Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис. 1.12.2).
| Рисунок 1.12.2. Деформация изгиба. |
Упругую силу действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры. При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому ее часто называют силой нормального давления. Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести: Сила с которой тело действует на стол, называется весом тела.
В технике часто применяются спиралеобразные пружины (рис. 1.12.3). При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром. Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба.
В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Для металлов относительная деформация ε = x / l не должна превышать 1 %. При больших деформациях возникают необратимые явления (текучесть) и разрушение материала.
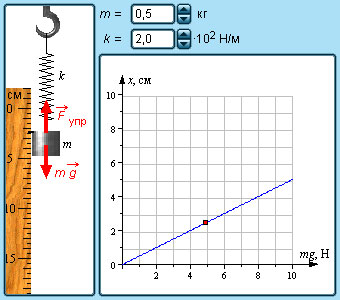 |
Модель. |
1°. Деформация
Деформацией твердого тела называется изменение его размеров и объема, которое сопровождается обычно изменением формы тела. К деформациям относятся растяжение, сжатие, кручение, сдвиг и изгиб.
1°.01 Механизм возникновения сил упругости
| Частицы тела (молекулы или атомы) взаимодействуют друг с другом силами притяжения и отталкивания, имеющими электромагнитное происхождение. Силы взаимодействия зависят от расстояний между частицами. Если деформации нет, то силы притяжения компенсируются силами отталкивания. При деформации изменяются расстояния между частицами, и баланс сил взаимодействия нарушается. Например, при растяжении стержня расстояния между его частицами увеличиваются, и начинают преобладать силы притяжения. Наоборот, при сжатии стержня расстояния между частицами уменьшаются, и начинают преобладать силы отталкивания. В любом случае возникает сила, которая направлена в сторону, противоположную деформации, и стремится восстановить первоначальную конфигурацию тела. |
2°. Упругие и пластические деформации
| Деформации бывают упругими и пластическими. Упругая деформация полностью исчезает после снятия внешнего воздействия, которое вызвало деформацию. В результате деформированное поначалу тело восстанавливает свои первоначальные размеры и форму. Пластическая деформация сохраняется (быть может,частично) после снятия внешней на-грузки,и тело уже не возвращается к прежним размерами форме. |
3°. Сила упругости
Силой упругости Fупр называется сила, возникающая при деформации тела.
![]()
В большинстве задач элементарного курса физики рассматриваются, либо МАКРО-деформации растяжения или сжатия, и тогда мы обозначаем эти силы как Fупр и рассматриваем их с точки зрения закона Гука.s
Либо рассматриваются силы упругости возникающие при МИКРО-деформациях, и тогда мы обозначаем их как N (реакция опоры) или T (сила натяжения) и закон Гука к ним, как правило не применяем.
4°. Абсолютная деформация
Абсолютная деформация характеризует изменение линейных размеров тела. Чаще всего в задачах используется модуль абсолютной деформации он обозначается Δx и определяется как
| (4.01) |
![]()
5°. Значение силы упругости, Закон Гука
Для упругого растяжения или сжатия, характеризующегося некоторым значение модуля абсолютной деформации, сила упругости пропорциональна модулю абсолютной деформации.
![]()
Математически закон Гука записывается следующим образом:
| (5.01) |
где k – коэффициент жесткости, [k] = Н/м
Δx – модуль абсолютной деформации
6°. Направление силы упругости
Сила упругости направлена противоположно относительному смещению точек, деформируемого тела.
Например на рисунке выше правый конец пружины относительно системы отсчета связанной со стеной сместился вправо, следовательно сила упругости действующая на этот конец пружины будет направлена влево. Заметим, что в системе отсчета связанной с телом, все будет наоборот, относительно тела (шарика) левый конец смещается вправо и, следовательно, на него сила упругости будет действовать вправо.
Таким образом в полном соответствии с III законом Ньютона, силы упругости возникают парно, действуют на оба конца пружины и направлены противоположно друг другу.
![]()
Отметим, что силы натяжения T направлены всегда вдоль нити, силы реакции опоры N всегда направлены перпендикулярно к поверхностям соприкасающихся тел.
![]()
![]()
7°. Динамометр. Измерение сил.
Существуют различные способы измерения сил, но один из самых распространенных – измерение силы с помощью динамометра.
Идея способа очень проста. Один конец пружины мы фиксируем, ко второму прикладываем измеряемую силу Fвш. Под действием внешней силы пружина будет растягиваться, до тех пор пока не уравновесит внешнюю силу, следовательно измерив силу упругости, возникающую при деформации пружины, мы измерим внешнюю силу.
|
|
8°. Вес тела
В результате действия тела на опору возникает сила упругости, которую мы называем реакция опоры, но по третьему закону Ньютона (§2.05) , если опора действует на тело, то должна быть сила и со стороны тела на опору и такая сила действительно есть – это вес тела P.
| (8.01) |
Вес тела — это сила, с которой тело действует на опору или подвес. Подчеркнём, что вес приложен не к телу, а к опоре (подвесу).
![]()
8°.01 Вес тела. Невесомость
Рассмотрим тело, находящееся в поле силы тяжести. Предположим, что есть опора или подвес, препятствующие свободному падению тела.
Рассмотрим два случая, когда тело движется ускоренно вверх, и ускоренно вниз.
Второй закон Ньютона в обоих случаях имеет вид:
| (8.02) |
так как на тело в обоих случаях действуют лишь две силы – сила тяжести mg и реакция опоры N (см. рис. ниже)
Первый случай.
![]()
Запишем
Ось направим вертикально вверх по ускорению (правило выбора направления оси ). Тогда в проекции на ось OY уравнение (4.01) примет вид
и
| (8.04) |
так реакция опоры N по III Закону Ньютона всегда равна весу тела P то можем записать для веса в этом случае
| (8.05) |
Таким образом при вертикальном движении с некоторым ускорением направленным вертикально вверх, тело находящееся на поверхности испытывает перегрузку , т.е. его вес будет больше силы тяжести.
Примечание
Состояние перегрузки часто характеризуют коэффициентом при g , например, говорят 2g когда хотят сказать что вес в два раза больше силы тяжести или 3g когда вес в три раза больше и т.д. Отметим, что состояние перегрузки теснейшим образом связно с целостностью или наоборот, разрушением тела. Любое тело можно охарактеризовать коэффициентом при g, при котором оно разрушается. Так в частности, человек способен кратковременно выдержать состояние перегрузки в 9g. Такие перегрузки (и выше) могут возникать при ударах во время падения или же ударах сопровождающих различные дорожно-транспортные происшествия.
Второй случай.
![]()
Спроецировав II закон Ньютона на ось OY и учтя что вес равен реакции опоры, получим для этого случая
| (8.10) |
Таким образом при вертикальном движении с некоторым ускорением направленным вертикально вниз, тело находящееся на поверхности имеет вес меньше чем сила тяжести.
При условии что
т.е. при свободном падении, вес тела обращается в нуль. Это — состояние невесомости, при котором тело вообще не давит на опору.
Вопрос на понимание: Космонавты приземляются на Луне двигаясь равнозамедленно. Что они испытывают невесомость или перегрузку?
Ответ.
Будет ли иметь место «перегрузка» или «невесомость» зависит от направления ускорения, (не скорости). Так как движение замедленное, направления скорости и ускорения противоположны следовательно, ускорение направлено вверх и они испытывают перегрузку.
Пример №1
На тело массой m, находящееся на горизонтальной поверхности, через систему нитей и пружину жесткостью k действует сила F. Найти удлинение пружины и ускорение тела.
![]()
Решение
уберем «лишние» нити (в соответствии с 9°.1)
![]()
покажем силы в точках D и B
![]()
применим II з. Ньютона к точке. B
Учтем, что масса точки равна нулю (в соответствии с 9°.5), ось OX направим вправо
| (10.01) |
откуда
| (10.02) |
учитывая, что силы упругости на концах пружины равны по модулю и противоположны по направлению
| (10.03) |
Соотношением (10.03) мы показали, что пружина передает внешнюю силу без изменения с одного конца на другой
Модуль силы, действующей на тело, может быть выражен через закона Гука.
откуда
| (10.05) |
Отметим что модуль абсолютной деформации пружины не зависит от массы тела.
Что бы найти ускорение тела, применим к нему II закон Ньютона. С учетом (10.03) можем записать
| (10.06) |
откуда ускорение
| (10.07) |
Отметим, что ускорение не зависит от каких либо характеристик нити или пружины, очевидный результат, подтверждающий, что нить, как и пружина, это лишь посредник позволяющий передать воздействие из одной точки в другую.
Пример №2
Два груза соединены нитью. К каждому грузу прикреплена пружина. Концы пружин, в свою очередь крепятся к левой и правой стене. Обе пружины находятся в растянутом состоянии. Известны величины абсолютных деформаций пружин и их жесткости. Необходимо найти силу натяжения нити. Вся система покоится, трения нет.
![]()
Решение
Расставим силы
![]()
Выясним как направлена сила упругости нити в А.
Поместим в эту область виртуальную пружинку и посмотрим что с не будет происходить («лишние» силы убраны с рисунка)
![]()
Под действием силы упругости левой пружинки второе тело «стремится» сместится влево, под действием силы упругости правой пружинки первое тело «стремится» сместится вправо и, следовательно наша виртуальная пружинка будет растягиваться. Покажем силы упругости создаваемые виртуальной пружинкой.
![]()
Из рисунка видим, что на второе тело сила упругости со стороны нити действует вправо (показана более темным зеленым цветом). Аналогично рассуждая, получим что на первое тело действует сила упругости нити направленная влево. Причем эти силы упругости будут равны по модулю.
![]()
На рисунке все силы, кроме парных показаны с разной длинной, но это лишь говорит, что мы пока не знаем как они соотносятся. Ответим на этот вопрос.
Так как второе тело покоится следовательно
| (10.08) |
Так как первое тело покоится следовательно
| (10.09) |
Силы натяжения нити одинаковы по модулю
| (10.10) |
Следовательно силы упругости левой пружины равны по модулю силам упругости правой пружины.
| (10.11) |
Т.е. все силы будут одинаковы по модулю
И для того что бы найти силу натяжения, достаточно найти из закона Гука любую из сил упругости пружин действующих на тело.
Например.
| (10.12) |
Задача решена.
[totalpoll id=”5455″]
