Какое свойство серединного перпендикуляра к отрезку вы знаете
На данном уроке мы рассмотрим теорему о пересечении биссектрис треугольника. Также сформулируем и докажем прямую и обратную теоремы о серединном перпендикуляре. После этого рассмотрим теорему о пересечении серединных перпендикуляров треугольника.
Теорема о пересечении биссектрис треугольника
На предыдущем уроке мы рассмотрели свойства биссектрисы угла как заключенного в треугольник, так и свободного. Треугольник включает в себя три угла и для каждого из них рассмотренные свойства биссектрисы сохраняются.
Теорема:
Биссектрисы АА1, ВВ1, СС1 треугольника пересекаются в одной точке О (рис. 1).
Рис. 1. Иллюстрация к теореме
Доказательство:
Рассмотрим сначала две биссектрисы ВВ1 и СС1. Они пересекаются, точка пересечения О существует. Чтобы доказать это, предположим противное: пусть данные биссектрисы не пересекаются, в таком случае они параллельны. Тогда прямая ВС является секущей и сумма углов , это противоречит тому, что во всем треугольнике сумма углов .
Итак, точка О пересечения двух биссектрис существует. Рассмотрим ее свойства:
Точка О лежит на биссектрисе угла , значит, она равноудалена от его сторон ВА и ВС. Если ОК – перпендикуляр к ВС, OL – перпендикуляр к ВА, то длины этих перпендикуляров равны – . Также точка О лежит на биссектрисе угла и равноудалена от его сторон CВ и СА, перпендикуляры ОМ и ОК равны.
Получили следующие равенства:
, то есть все три перпендикуляра, опущенные из точки О на стороны треугольника, равны между собой.
Нас интересует равенство перпендикуляров OL и ОМ. Это равенство говорит о том, что точка О равноудалена от сторон угла , отсюда следует, что она лежит на его биссектрисе АА1.
Таким образом, мы доказали, что все три биссектрисы треугольника пересекаются в одной точке.
Кроме того, треугольник состоит из трех отрезков, значит, нам следует рассмотреть свойства отдельного отрезка.
Задан отрезок АВ. У любого отрезка есть середина, и через нее можно провести перпендикуляр – обозначим его за р. Таким образом, р – серединный перпендикуляр.
Прямая теорема о серединном перпендикуляре
Рис. 2. Иллюстрация к теореме
Любая точка, лежащая на серединном перпендикуляре, равноудалена от концов отрезка.
Доказать, что (рис. 2).
Доказательство:
Рассмотрим треугольники и . Они прямоугольные и равные, т. к. имеют общий катет ОМ, а катеты АО и ОВ равны по условию, таким образом, имеем два прямоугольных треугольника, равных по двум катетам. Отсюда следует, что гипотенузы треугольников тоже равны, то есть, , что и требовалось доказать.
Справедлива обратная теорема.
Обратная теорема о серединном перпендикуляре
Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.
Задан отрезок АВ, серединный перпендикуляр к нему р, точка М, равноудаленная от концов отрезка. Доказать, что точка М лежит на серединном перпендикуляре к отрезку (рис. 3).
Рис. 3. Иллюстрация к теореме
Доказательство:
Рассмотрим треугольник . Он равнобедренный, так как по условию. Рассмотрим медиану треугольника: точка О – середина основания АВ, ОМ – медиана. Согласно свойству равнобедренного треугольника, медиана, проведенная к его основанию, является одновременно высотой и биссектрисой. Отсюда следует, что . Но прямая р также перпендикулярна АВ. Мы знаем, что в точку О можно провести единственный перпендикуляр к отрезку АВ, значит прямые ОМ и р совпадают, отсюда следует, что точка М принадлежит прямой р, что и требовалось доказать.
Прямую и обратную теоремы можно обобщить.
Теорема о пересечении серединных перпендикуляров треугольника
Точка лежит на серединном перпендикуляре к отрезку тогда и только тогда, когда она равноудалена от концов этого отрезка.
Итак, повторим, что в треугольнике три отрезка и к каждому из них применимо свойство серединного перпендикуляра.
Теорема:
Серединные перпендикуляры треугольника пересекаются в одной точке.
Задан треугольник . Перпендикуляры к его сторонам: Р1 к стороне ВС, Р2 к стороне АС, Р3 к стороне АВ.
Доказать, что перпендикуляры Р1, Р2 и Р3 пересекаются в точке О (рис. 4).
Рис. 4. Иллюстрация к теореме
Доказательство:
Рассмотрим два серединных перпендикуляра Р2 и Р3, они пересекаются, точка пересечения О существует. Докажем этот факт от противного – пусть перпендикуляры Р2 и Р3 параллельны. Тогда угол развернутый, что противоречит тому факту, что сумма трех углов треугольника составляет . Итак, существует точка О пересечения двух из трех серединных перпендикуляров. Свойства точки О: она лежит на серединном перпендикуляре к стороне АВ, значит, она равноудалена от концов отрезка АВ: . Также она лежит на серединном перпендикуляре к стороне АС, значит, . Получили следующие равенства:
Из данного равенства нас интересует тот факт, что , это значит, что точка О равноудалена от концов отрезка ВС, значит, она принадлежит серединному перпендикуляру к стороне ВС. Таким образом, точка О – точка пересечения трех серединных перпендикуляров треугольника , что и требовалось доказать.
Выводы по уроку
Итак, мы рассмотрели теорему о пересечении биссектрис треугольника. Сформулировали и доказали теорему о свойстве серединного перпендикуляра. Рассмотрели теорему о пересечении серединных перпендикуляров треугольника.
Список литературы
- Александров А.Д. и др. Геометрия 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия 8. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Bymath.net (Источник).
- Oldskola1.narod.ru (Источник).
Домашнее задание
- Задание 1 – Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др., Геометрия 7–9, № 679–681, с. 180.
- Задание 2 – докажите, что если в треугольнике совпадают точка пересечения биссектрис и серединных перпендикуляров к сторонам, то он равносторонний;
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Окружность
- Свойства серединного перпендикуляра к отрезку
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.
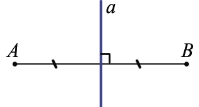
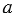 — серединный перпендикуляр к отрезку АВ.
— серединный перпендикуляр к отрезку АВ.
Теорема
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
Обратно: каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему.
Доказательство
1) Дано: m — серединный перпендикуляр отрезка АВ, О — середина АВ, М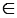 m
m
Доказать: АМ = ВМ
Доказательство:
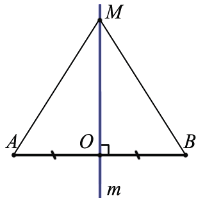
Если О = М, то АМ = ВМ, т.к. О — середина АВ.
Пусть О 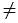 М. Рассмотрим
М. Рассмотрим  ОАМ и
ОАМ и  ОВМ: так как m — серединный перпендикуляр отрезка АВ, то рассматриваемые треугольники прямоугольные. ОА = ОВ, т.к. О — середина отрезка АВ, ОМ — общий катет, следовательно,
ОВМ: так как m — серединный перпендикуляр отрезка АВ, то рассматриваемые треугольники прямоугольные. ОА = ОВ, т.к. О — середина отрезка АВ, ОМ — общий катет, следовательно,  ОАМ =
ОАМ =  ОВМ, по двум катетам, а в равных треугольниках против соответственно равных углов лежат равные стороны, поэтому АМ = ВМ.
ОВМ, по двум катетам, а в равных треугольниках против соответственно равных углов лежат равные стороны, поэтому АМ = ВМ.
2) Дано: m — серединный перпендикуляр отрезка АВ, О — середина АВ, АN = ВN
Доказать:N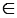 m
m
Доказательство:
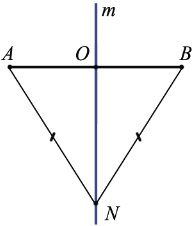
Рассмотрим произвольную точку N.
Если N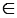 АВ, то N = О, а, значит, она лежит на прямой m.
АВ, то N = О, а, значит, она лежит на прямой m.
Если N не лежит на АВ, то  ANB — равнобедренный, так как АN = ВN. О — середина АВ, следовательно, NО — медиана
ANB — равнобедренный, так как АN = ВN. О — середина АВ, следовательно, NО — медиана  ANB, а, значит, и высота по свойству равнобедренного треугольника. Поэтому NО
ANB, а, значит, и высота по свойству равнобедренного треугольника. Поэтому NО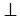 АВ, следовательно, прямые NО и m совпадают, так как по устовию m — серединный перпендикуляр отрезка АВ, т.е. N — точка прямой m. Теорема доказана.
АВ, следовательно, прямые NО и m совпадают, так как по устовию m — серединный перпендикуляр отрезка АВ, т.е. N — точка прямой m. Теорема доказана.
Следствие 1
Следствие2
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Взаимное расположение прямой и окружности
Касательная к окружности
Градусная мера дуги окружности
Теорема о вписанном угле
Свойство биссектрисы угла
Теорема о пересечении высот треугольника
Вписанная окружность
Описанная окружность
Окружность
Правило встречается в следующих упражнениях:
7 класс
Задание 679,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 680,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 686,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 19,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 20,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 720,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1085,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 12,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1172,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1241,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
На данном уроке мы подробно рассмотрим, какими свойствами обладают точки, лежащие на биссектрисе угла, и точки, которые лежат на серединном перпендикуляре к отрезку.
Тема: Окружность
Урок: Свойства биссектрисы угла и серединного перпендикуляра к отрезку
1. Свойство биссектрисы угла, прямая и обратная теорема
Рассмотрим свойства точки, лежащей на биссектрисе угла (см. Рис. 1).
Рис. 1
Задан угол , его биссектриса AL, точка М лежит на биссектрисе.
Теорема:
Если точка М лежит на биссектрисе угла, то она равноудалена от сторон угла, то есть расстояния от точки М до АС и до ВС сторон угла равны.
Доказательство:
Расстояние от точки до прямой есть длина перпендикуляра. Проведем из точки М перпендикуляры МК к стороне АВ и МР к стороне АС.
Рассмотрим треугольники и . Это прямоугольные треугольники, и они равны, т.к. имеют общую гипотенузу АМ, а углы и равны, так как AL – биссектриса угла . Таким образом, прямоугольные треугольники равны по гипотенузе и острому углу, отсюда следует, что , что и требовалось доказать. Таким образом, точка на биссектрисе угла равноудалена от сторон этого угла.
Справедлива обратная теорема.
2. Теорема о пересечении биссектрис треугольника
Если точка равноудалена от сторон неразвернутого угла, то она лежит на его биссектрисе.
Рис. 2
Задан неразвернутый угол , точка М, такая, что расстояние от нее до сторон угла одинаковое (см. Рис. 2).
Доказать, что точка М лежит на биссектрисе угла.
Доказательство:
3. Свойство серединного перпендикуляра, прямая и обратная теоремы
Расстояние от точки до прямой есть длина перпендикуляра. Проведем из точки М перпендикуляры МК к стороне АВ и МР к стороне АС.
Рассмотрим треугольники и . Это прямоугольные треугольники, и они равны, т.к. имеют общую гипотенузу АМ, катеты МК и МР равны по условию. Таким образом, прямоугольные треугольники равны по гипотенузе и катету. Из равенства треугольников следует равенство соответствующих элементов, против равных катетов лежат равные углы, таким образом, , следовательно, точка М лежит на биссектрисе данного угла.
Прямую и обратную теоремы можно объединить.
Теорема
Биссектриса неразвернутого угла есть геометрическое место точек, равноудаленных от сторон данного угла.
Теорема
Биссектрисы АА1, ВВ1, СС1 треугольника пересекаются в одной точке О (см. Рис. 3).
Рис. 3
Доказательство:
Рассмотрим сначала две биссектрисы ВВ1 и СС1. Они пересекаются, точка пересечения О существует. Чтобы доказать это, предположим противное – пусть данные биссектрисы не пересекаются, в таком случае они параллельны. Тогда прямая ВС является секущей, и сумма углов , это противоречит тому, что во всем треугольнике сумма углов .
Итак, точка О пересечения двух биссектрис существует. Рассмотрим ее свойства:
Точка О лежит на биссектрисе угла , значит, она равноудалена от его сторон ВА и ВС. Если ОК – перпендикуляр к ВС, OL – перпендикуляр к ВА, то длины этих перпендикуляров равны – . Также точка О лежит на биссектрисе угла и равноудалена от его сторон CВ и СА, перпендикуляры ОМ и ОК равны.
Получили следующие равенства:
, то есть все три перпендикуляра, опущенные из точки О на стороны треугольника, равны между собой.
Нас интересует равенство перпендикуляров OL и ОМ. Это равенство говорит о том, что точка О равноудалена от сторон угла , отсюда следует, что она лежит на его биссектрисе АА1.
Таким образом, мы доказали, что все три биссектрисы треугольника пересекаются в одной точке.
Перейдем к рассмотрению отрезка, его серединного перпендикуляра и свойства точки, которая лежит на серединном перпендикуляре.
Задан отрезок АВ, р – серединный перпендикуляр. Это значит, что прямая р проходит через середину отрезка АВ и перпендикулярна ему.
Теорема
Рис. 4
Любая точка, лежащая на серединном перпендикуляре, равноудалена от концов отрезка (см. Рис. 4).
Доказать, что
Доказательство:
Рассмотрим треугольники и . Они прямоугольные и равные, т.к. имеют общий катет ОМ, а катеты АО и ОВ равны по условию, таким образом, имеем два прямоугольных треугольника, равных по двум катетам. Отсюда следует, что гипотенузы треугольников тоже равны, то есть , что и требовалось доказать.
Заметим, что отрезок АВ является общей хордой для многих окружностей.
Например, первая окружность с центром в точке М и радиусом МА и МВ; вторая окружность с центром в точке N, радиусом NA и NB.
Таким образом, мы доказали, что если точка лежит на серединном перпендикуляре к отрезку, она равноудалена от концов отрезка (см. Рис. 5).
Рис. 5
Справедлива обратная теорема.
Теорема
Если некоторая точка М равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
Задан отрезок АВ, серединный перпендикуляр к нему р, точка М, равноудаленная от концов отрезка (см. Рис. 6).
Доказать, что точка М лежит на серединном перпендикуляре к отрезку.
Рис. 6
Доказательство:
Рассмотрим треугольник . Он равнобедренный, так как по условию. Рассмотрим медиану треугольника: точка О – середина основания АВ, ОМ – медиана. Согласно свойству равнобедренного треугольника, медиана, проведенная к его основанию, является одновременно высотой и биссектрисой. Отсюда следует, что . Но прямая р также перпендикулярна АВ. Мы знаем, что в точку О можно провести единственный перпендикуляр к отрезку АВ, значит, прямые ОМ и р совпадают, отсюда следует, что точка М принадлежит прямой р, что и требовалось доказать.
Прямую и обратную теоремы можно обобщить.
Теорема
Серединный перпендикуляр к отрезку есть геометрическое место точек, равноудаленных от его концов.
Треугольник, как известно, состоит из трех отрезков, значит, в нем можно провести три серединных перпендикуляра. Оказывается, что они пересекаются в одной точке.
4. Теорема о пересечении серединных перпендикуляров в треугольнике
Серединные перпендикуляры треугольника пересекаются в одной точке.
Задан треугольник . Перпендикуляры к его сторонам: Р1 к стороне ВС, Р2 к стороне АС, Р3 к стороне АВ (см. Рис. 7).
Доказать, что перпендикуляры Р1, Р2 и Р3 пересекаются в точке О.
Рис. 7
Доказательство:
Рассмотрим два серединных перпендикуляра Р2 и Р3, они пересекаются, точка пересечения О существует. Докажем этот факт от противного – пусть перпендикуляры Р2 и Р3 параллельны. Тогда угол развернутый, что противоречит тому факту, что сумма трех углов треугольника составляет . Итак, существует точка О пересечения двух из трех серединных перпендикуляров. Свойства точки О: она лежит на серединном перпендикуляре к стороне АВ, значит, она равноудалена от концов отрезка АВ: . Также она лежит на серединном перпендикуляре к стороне АС, значит, . Получили следующие равенства:
Из данного равенства нас интересует тот факт, что , это значит, что точка О равноудалена от концов отрезка ВС, значит, она принадлежит серединному перпендикуляру к стороне ВС. Таким образом, точка О – точка пересечения трех серединных перпендикуляров треугольника , что и требовалось доказать.
5. Выводы по уроку
Итак, мы рассмотрели свойства биссектрисы угла и серединного перпендикуляра к отрезку, доказали некоторые теоремы. Далее мы рассмотрим свойства пересечения высот треугольника.
Список литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Bymath.net (Источник).
- Oldskola1.narod.ru (Источник).
Домашнее задание
- Задание 1: биссектрисы внешних углов при вершинах В и С треугольника пересекаются в точке О. Докажите, что луч АО – биссектриса угла
- Задание 2: биссектрисы АА1 и ВВ1 треугольника пересекаются в точке О. Найдите угол , если угол .
- Задание 3: биссектриса угла равнобедренного треугольника с основанием ВС пересекает серединный перпендикуляр к стороне АС в точке О. Найдите ВО, если
Голосование за лучший ответ
Бенефис мартовской кошки
Просветленный
(39701)
8 лет назад
Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку.
Свойства серединных перпендикуляров треугольника
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.
Ангелина ГребенкинаУченик (101)
5 лет назад
Утверждение верное, но не объяснимое, что же такое «Серединный перпендикуляр» это пояснение было поверхностным. Была бы я, ученицей не читала б !
Алекс
Ученик
(195)
4 года назад
Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку.
Свойства серединных перпендикуляров треугольника
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого
Евгения Тихомирова
Профи
(692)
4 года назад
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину отрезка и перпендикулярная к нему. На рисунке 106 прямая a – серединный перпендикуляр к отрезку AB. Докажем теорему о серединном перпендикуляре к отрезку.
Теорема. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
Доказательство. Обозначим буквой M произвольную точку серединного перпендикуляра a к отрезку AB и докажем, что AM = BM.
Если точка M совпадает с серединой O отрезка AB, то справедливость равенства AM = BM очевидна. Если же M и O – различные точки, то прямоугольные треугольники OAM и OBM (рис. 107) равны по двум катетам, поэтому AM = BM. Теорема доказана.
https://mthm.ru/images/geometry7/pic106-107.png
Кристина Глухова
Ученик
(132)
4 года назад
Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку.
Свойства серединных перпендикуляров треугольника
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.
равиль давлетхузин
Профи
(537)
3 года назад
Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку.
Свойства серединных перпендикуляров треугольника
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.
Даша Бец
Знаток
(263)
2 года назад
Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку.
Свойства серединных перпендикуляров треугольника
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.
