Какое свойство отрезка геометрия 7 класс

- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Начальные геометрические сведения
- Длина отрезка
Отрезок — это геометрическая фигура, которая имеет начало и конец, значит отрезки можно измерять.
Измерить отрезок — значит найти его длину(расстояние между его концами).
Для того, чтобы найти длину отрезка, его сравнивают с отрезком принятым за единицу измерения, который носит название единичный отрезок.
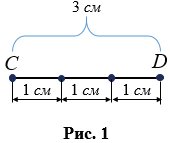
Если за единицу измерения принять сантиметр, то, чтобы определить длину отрезка, нужно узнать сколько раз в этом отрезке укладывается сантиметр. На рис.1 в отрезке СD сантиметр укладывается ровно три раза, значит, длина отрезка СD равна 3 см, можно записать СD = 3 см. В данном случае, для измерения удобно использовать сантиметровую линейку.
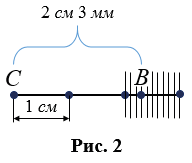
Бывает, что единичный отрезок не укладывается целое число раз в измеряемый отрезок, тогда единичный отрезок делят на 10 равных частей и определяют сколько раз одна десятая часть укладывается в остатке измеряемого отрезка. На рис.2 в отрезке СВ сантиметр укладывается 2 раза и в остатке 3 раза укладывается одна десятая часть сантиметра, значит, длина отрезка СВ равна 3,3 см или, учитывая что для сантиметра десятая часть равна миллиметру, 3 см 3 мм, т.е. можно записать СВ = 3,3 см (СВ = 3 см 3 мм).
Может получится так, что и в миллиметрах остаток не укладывается целое число раз, тогда:
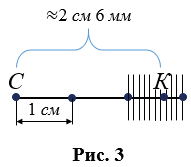
- Если нужны более точные измерения, то процесс деления продолжается, т.е. миллиметр также можно разделить на 10 равных частей и т.д. Такая точность в повседневной жизни не нужна, поэтому пользуются приближенными значениями, но имеет важную роль при проведении каких-либо исследований для совершения научных открытий.
За единицу измерения можно принимать не только сантиметр, но и другие отрезки, например, дециметр, метр и т.д.
Длина отрезка — это всегда какое-то положительное число.
Свойства длин отрезков:
- Равные отрезки имеют равные длины.
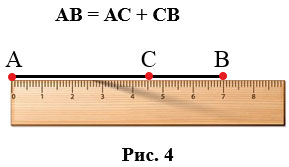
- Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих двух отрезков. Так на Рис.4 точка С делит отрезок АВ на два отрезка АС и СВ. Приложим линейку и видим, что АС = 4,5 см, СВ = 2,5 см, АВ = 7 см, т.е. АС + СВ = АВ.
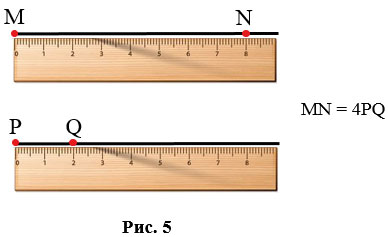
- Если длина одного отрезка MN в n раз больше длины другого отрезка PQ, то записывают MN = nPQ. На Рис.5 даны два отрезка MN и PQ, приложим к ним линейку и видим, что MN = 8 см, PQ = 2 см, т.е. MN больше PQ в 4 раза, тогда можно записать, что MN = 4PQ.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Точки, прямые, отрезки
Провешивание прямой на местности
Луч
Угол
Равенство геометрических фигур
Сравнение отрезков
Сравнение углов
Единицы измерения длины, расстояний
Градусная мера угла
Измерение углов на местности
Смежные углы
Вертикальные углы
Перпендикулярные прямые
Построение прямых углов на местности
Начальные геометрические сведения
Правило встречается в следующих упражнениях:
7 класс
Задание 25,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 28,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 30,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 31,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 37,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 76,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 77,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 98,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 801,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
МБОУ «Апраксинская СОШ»
Урок по теме
“Измерение отрезков»
(геометрия, 7 класс)
(с презентацией)
Подготовила и провела: Алякина Е.И.
2017
Разработка урока геометрии в 7 классе.
Тема урока: Измерение отрезков
Цели:
- Познакомить учащихся с процедурой измерения отрезков, рассмотреть свойства длин отрезка, познакомить с различными единицами измерения и инструментами для измерения отрезков,
- Развивать умение измерять без инструментов.
Оборудование: компьютер, проектор, экран; линейки, циркуль, рулетка.
Урок сопровождается презентацией
Ход урока
1. Организационный момент. Слайд 1
2. Актуализация знаний. Фронтальный опрос. Слайд 2
1. Сколько прямых можно провести через две точки?
2. Сколько общих точек могут иметь две прямые?
3. Объясни, что такое отрезок.
4. Объясни, что такое луч. Как обозначаются лучи?
5. Какая фигура называется углом? Объясни, что такое вершина и стороны угла.
6. Какой угол называется развернутым?
7. Какие фигуры называются равными?
8. Объясните, как сравнить два отрезка?
9. Какая точка называется серединой отрезка?
10. Объясните, как сравнить два угла?
11. Какой луч называется биссектрисой угла?
3. Мотивация к деятельности. Определение темы и цели урока.
Слайд 3
Один средневековый философ Марсилио Сичино сказал: «Измерь самого себя – и ты станешь настоящим геометром!» Как вы понимаете это высказывание? (Обсуждение)
Каждому человеку неоднократно приходилось что-то измерять: высоту дерева, собственный вес, длину прыжка, скорость и многое другое. С точки зрения геометрии мы имеем в таких случаях дело с измерением отрезков.
Слайд 4
Запись темы урока: Измерение отрезков
Слайд 5
Постановка цели: познакомиться с процедурой измерения отрезков, рассмотреть свойства длин отрезка, познакомиться с различными единицами измерения длины и инструментами для измерения отрезков, узнать, как можно измерять без инструментов.
Измерения производят в определённых единицах: длину – измеряют в единицах длины, вес – в единицах веса и т.д.
Слайд 6
– Ч то значит измерить какую-то величину?
Это значит – сравнить ее с неким эталоном.
Измерение — это сравнивание объекта измерения с выбранной единицей измерения.
Слайд 7
Как известно, герои одного мультфильма измеряли длину удава в попугаях. Для обитателей тропического леса, в котором живет попугай, эта единица ничуть не хуже других. Но длина в попугаях ничего не скажет жителям тайги.
Слайд 8
Эта история из мультфильма не такая уж нелепая. Правители разных стран любили устанавливать свои меры, часто связанные с собственной персоной.
Слайд 9
Например, английский король Генрих I ввел в качестве единиц длины ЯРД – расстояние от кончика своего носа до большого пальца вытянутой руки.
Более демократична по происхождению другая английская единица длины ФУТ, что по-английски означает «ступня». 16 англичан выстраивались в цепочку таким образом, что каждый следующий касался концами пальцев своих ног пяток предыдущего. 1/16 такой цепочки и составляла 1 фут.
Слайд 10
На Руси в старину мерой длины был ШАГ, ПЯДЬ: Малая пядь равнялась расстоянию между концами растянутых пальцев, большего и указательного (~19 см), большая пядь – расстояние между раздвинутым большим пальцем и мизинцем (~ 23 см),
Слайд 11
ЛАДОНЬ – ширина кисти руки, ЛОКОТЬ – расстояние от локтя до конца среднего пальца.
Слайд 12
Большие расстояния измерялись ПОЛЕТОМ СТРЕЛЫ.
Несколько позже появился АРШИН, с персидского – локоть (~71 см), существовал персидский аршин, турецкий аршин и др., отсюда и появилась поговорка «Мерить на свой аршин».
Аршин делился на 16 вершков,
Слайд 13
3 аршина составляли САЖЕНЬ – расстояние от ступни до конца среднего пальца вытянутой вверх руки, 500 саженей – составляли ВЕРСТУ (или поприще), 7 верст – МИЛЮ.
Слайд 14
С развитием производства и торговли люди убедились в том, что не всегда удобно измерять расстояния шагами или прикладыванием локтя, так как длина локтя или шага у разных людей различная, а мера длины должна быть постоянной. Так появился метр.
Метр, принятий за эталон, сейчас хранится в одном из французских музеев.
Так что же значит «измерить»?
Слайд 15
Коротко можно ответить так: «Измерить – значит сравнить с эталоном».
4. Инструменты
Слайд 16
А чем мы обычно измеряем? Сравниваем?
К древнейшим геометрическим инструментам относятся циркуль и линейка. Сначала изобрели линейку, а циркуль был изобретен значительно позже. Фигуры папируса Ахмеса, например, свидетельствует о применении линейки, но не циркуля. Циркуль был изобретен в Древней Греции.
Слайд 17
В техническом черчении употребляют масштабную миллиметровую линейку. Для измерения диаметра трубки используют штангенциркуль.
Слайд 18
Для измерения расстояний на местности пользуются рулеткой.
«Рулетка» — термин французского происхождения (rouler – свертывать, катать).
5. Свойства длины отрезка.
Слайд 19
Попробуем выяснить некоторые свойства длины.
1. Какие отрезки нельзя начертить? а) 2,5 см, б) 7 см, в) — 4 см.
Длина отрезка выражается положительным числом.
2. Что можно сказать о длине двух равных отрезков?
Равные отрезки имеют равные длины.
3. Если начертить отрезок АВ, поставить на нём точку С, то получатся отрезки АС и СВ. Что можно узнать, сложив длины отрезков АС и СВ?
Длина всего отрезка равна сумме длин отрезков, из которых он состоит.
6. Решение задач
Слайд 20
Решим несколько задач на измерение отрезков.
1) (устно) На отрезке КМ поставлена точка О, КО = 7,9дм, ОМ=4,5дм. Найдите длину КМ.
2) (письменно) На отрезке АВ лежит точка С, АС = 3,6см, АВ = 9,8см. Найдите длину СВ.
Слайд 21
Образец оформления
Слайд 22
3) (устно) Определите длину отрезка MN, если LN=7,6см.
4. (устно) Отрезок ВС = 7м и РК = 0,8ВС, Найдите длину отрезка РК.
5. (устно) Отрезок DE = 13мм и DE = 0,1RT. Найдите RT.
Слайд 23
Решить самостоятельно
1) Точка М лежит на прямой ЕF между Е и F. Чему равна длина отрезка МF, если EF = 8,3cм, EM = 3,3cм? (Решение оформляется по образцу предыдущего) Ответ: MF=5см.
2) Отрезок АI, длина которого равна 8дм, разделен на равные части. Найти длину отрезка DH. Ответ: DH=4дм.
3) На отрезке LS лежат точки K и R так, что К лежит между L и R,
LK = 5,2см, LS = 18см и LK = KR. Найти RS. (Учитель проверяет решение и оформление каждого) Ответ: RS=7,6см.
Слайд 24
Решить задачи
6. Точки А, В и С лежат на одной прямой. Известно, что АВ=9см, ВС=11,5см.
Какой может быть длина отрезка АС?
Ответ: АС=20,5см или АС=2,5см
7. АС = 10мм, ВD=14мм, АD=16мм. Найдите ВС
Ответ: ВС=8мм.
8. АВ=4,6м, ВС=9,26м, DA=24,76м. Найдите CD
Ответ: CD=10,9м
8. Практическая работа «Живой метр».
Учтите: для обмеривания мелких расстояний следует помнить длину между концами расставленных большого пальца и мизинца. Должно быть известно вам наибольшее расстояние между концами указательного и среднего пальцев. Надо, наконец, знать и ширину своих пальцев, длину стопы, размах рук.
Измерьте следующие расстояния и запишите в тетрадь.
- пядь – расстояние между концами растянутых пальцев, большего и указательного (~19 см),
- локоть – расстояние от локтя до конца среднего пальца (~71 см).
- косая сажень (248см) – расстояние от пальцев левой ноги до конца пальцев поднятой правой руки,
- маховая сажень (176см) – расстояние между концами пальцев расставленных в стороны рук
- фут (ступня), рост, длина пояса и т.п.
Теперь давайте измерим окружающие нас предметы (по желанию: длину, ширину и высоту парты, тетрадь, доску, классную комнату и др.) тремя способами:
- Сначала определим длину «на глаз» без измерительных приборов;
- Затем измерим, зная «собственные» длины частей тела;
- Проверим с помощью измерительных инструментов, насколько ошиблись.
Обсуждение.
Ребята, полезно уметь не только измерять расстояния без мерной линейки, шагами, но и оценивать их прямо на глаз. Этот навык можно выработать только путём упражнений.
Попробуйте, выйдя с товарищами на дорогу, наметить какой-нибудь придорожный предмет и прикинуть – сколько до него шагов. Затем посчитайте шаги, чтобы определить, чья оценка ближе к истинной, тот и выиграл.
9. Итог урока. Рефлексия
– Что нового вы сегодня узнали?
Слайд 25
– Нам удалось реализовать цель урока?
Слайды 26, 27, 28
А теперь мини-тест «Дополни предложения».
– Какие знания, полученные на уроке, вы сможете в дальнейшем применять в жизни?
Слайд 29
10. Домашняя работа. Выставление оценок.
пп. 7-8 (стр. 13-16), №24, №25, №32, №33.
Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне
просто дать определения. Но на практике оказалось, что это не так.
Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так
и не пришли к единому определению.
Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом
их описывают.
Запомните!
![]()
Точка — элементарная фигура, не
имеющая частей.
Прямая состоит из множества
точек и простирается бесконечно
в обе стороны.

На рисунке изображена прямая a и точки D, F, G и
H. Точки F и G
лежат на прямой a.
Точки D и H
не
лежат на прямой a.
В тексте точку обозначают символом «(·)».
Принадлежность и непринадлежность точки
прямой обозначают символами «∈» и «∉». Знак принадлежности можно запомнить как
зеркальное отображение буквы «Э» или как знак евро «€» .
То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:
- (·)F ∈ a — точка F принадлежит прямой a (другими словами, точка F лежит на прямой a);
- (·)G ∈ a — точка G принадлежит прямой a;
- (·)D ∉ a — точка D не принадлежит прямой a (другими словами, точка D не лежит на прямой a);
- (·)H ∉ a — точка H не принадлежит прямой a.
Как обозначить прямую
Прямую обычно обозначают одной
маленькой латинской буквой.
Прямую, на которой отмечены
две точки, иногда обозначают
по названиям этих точек большими латинскими точками.

- На рисунке изображены:
- Прямая a
- Прямая f
- Прямая CH
- Прямая DK

Точки D, E и F — лежат на одной прямой, поэтому:
прямая DE,
прямая EF и
прямая DF —
это три разных имени одной и той же прямой.
Задача № 1 из учебника Атанасян 7-9 класс
Проведите прямую, обозначьте её буквой a и
отметьте точки A и B, лежащие на этой прямой, и
точки P, Q и R, не лежащие на ней. Опишите
взаимное расположение точек A, B, P, Q, R и
прямой a, используя символы ∈ и ∉.
Решение задачи
Проведём прямую.

Обозначим её буквой a.

Отметим точки (·)A и (·)B, лежащие на прямой a.

Отметим точки (·)P, (·)Q и (·)R, не лежащие на прямой a.

Опишем взаимное расположение точек и прямой.
- (·)A ∈ a
- (·)B ∈ a
- (·)P ∉ a
- (·)Q ∉ a
- (·)R ∉ a
Задача решена.
Как обозначается пересечение прямых

На рисунке прямые a и b
не пересекаются.
Прямые b и
c пересекаются.
Хотя на чертеже не видно, но прямые a и
c тоже пересекаются (это становится ясно, если мысленно
продолжить вниз прямые a и с).
В тексте пересечение прямых обозначают
символом ∩. Информацию на рисунке выше можно записать следующим образом:
- b ∩ c — прямые b и с пересекаются;
- a ∩ c — прямые a и с пересекаются.

Прямые e и g имеют общую точку M.
Другими словами, прямые пересекаются в точке M. Геометрическими обозначениями
пересечение прямых в точке записывается так:
e ∩ g = (·)M

Прямые e и f не имеют общей точки — т.е. они не
пересекаются.
Взаимное расположение прямой и точек
Запомните!
![]()
Через любые две точки можно
провести прямую, и притом
только одну.

Через одну точку (·)A можно провести
сколько угодно прямых.
Через две точки
(·)A и (·)B можно провести
только одну прямую.
Сколько общих точек имеют две прямые
Запомните!
![]()
Две прямые либо имеют только
одну общую точку, либо не имеют
общих точек.
Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.
Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e
нет общих точек, т.к. эти
прямые не пересекаются.
Второй случай расположения прямых

Возможен вариант, что прямые f и e
пересекаются и, значит, имеют одну общую точку (·)M.
Третий случай расположения прямых

Предположим, что прямые
f и e имеют две или больше общих точек.
Например, точки (·)A и (·)B.
Но мы знаем, что через две
точки можно провести только одну прямую. Значит,
прямые f и e совпадают и наше предположение, что
у двух прямых может быть две или более общих точек неверно.
Вывод: две прямые либо имеют только
одну общую точку, либо не имеют
общих точек.
Задача № 3 из учебника Атанасян 7-9 класс
Проведите три прямые так, чтобы каждые две из
них пересекались. Обозначьте все точки
пересечения этих прямых. Сколько получилось
точек? Рассмотрите все возможные случаи.
Решение задачи
Проведём две прямые a и b так, чтобы эти две
прямые пересекались, и обозначим точку
пересечения.

Как мы видим, точка пересечения только одна. Мы
можем провести третью прямую так, чтобы она
тоже проходила через эту точку пересечения.

Теперь прямая a пересекается
с прямой b,
прямая b пересекается с прямой c и
прямая c пересекается с прямой a.
В этом случае
у нас только одна точка
пересечения всех прямых — точка (·)D.
Но возможен и другой вариант. Мы можем провести третью прямую c так,
чтобы она не проходила через точку (·)D. Тогда
получится
три точки пересечения — (·)D, (·)E и (·)F.

Прямая a пересекается
с прямой b
в точке (·)D,
прямая b пересекается с прямой c в точке (·)F и
прямая c пересекается с прямой a
в точке (·)E. Условие задачи выполнено.
Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.
Ответ: точек пересечения получается одна или
три.
Что такое отрезок
Запомните!
![]()
Отрезок —
часть прямой, ограниченная
двумя точками.

Две точки, ограничивающие отрезок, называются
концами отрезка. У отрезка на рисунке выше концы
называются S и
T.
Сам отрезок можно назвать ST
или TS. Когда изображают отрезок, оставшиеся от
прямой хвосты можно не рисовать.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.
