Какое свойство механического движения характеризует скорость
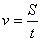
Механика – раздел физики, в котором изучают механическое движение.
Механику подразделяют на кинематику, динамику и статику.
Кинематикойназывают раздел механики, в котором движение тел рассматривается без выяснения причин этого движения. Кинематика изучает способы описания движения и связь между величинами, характеризующими эти движения.
Задача кинематики: определение кинематических характеристик движения (траектории движения, перемещения, пройденного пути, координаты, скорости и ускорения тела), а также получение уравнений зависимости этих характеристик от времени.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Механическое движение относительно, выражение «тело движется» лишено всякого смысла, пока не определено, относительно чего рассматривается движение. Движение одного и того же тела относительно разных тел оказывается различным. Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета. Покой тоже относителен (примеры: пассажир в покоящемся поезде смотрит на проходящий мимо поезд)
Главная задача механики – уметь вычислять координаты точек тела в любой момент времени.
Чтобы решить эту надо иметь тело, от которого ведется отсчет координат, связать с ним систему координат и иметь прибор для измерения промежутков времени.
Система координат, тело отсчета, с которым она связана, и прибор для отсчета времени образуют систему отсчета, относительно которой и рассматривается движение тела.
Системы координат бывают:
1. одномерная – положение тела на прямой определяется одной координатой x.

2. двумерная – положение точки на плоскости определяется двумя координатами x и y.
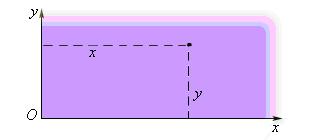
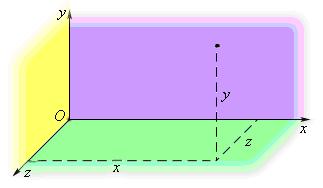
3. трехмерная – положение точки в пространстве определяется тремя координатами x, y и z.
Всякое тело имеет определенные размеры. Различные части тела находятся в разных местах пространства. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать его материальной точкой. Так можно поступать, например, при изучении движения планет вокруг Солнца.
Если все части тела движутся одинаково, то такое движение называется поступательным.
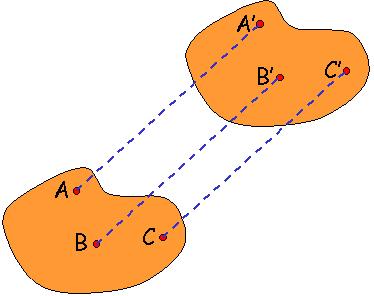
Поступательно движутся, например, кабины в аттракционе «Гигантское колесо», автомобиль на прямолинейном участке пути и т. д. При поступательном движении тела его также можно рассматривать как материальную точку.
Материальной точкой называется тело, размерами которого в данных условиях можно пренебречь.
Понятие материальной точки играет важную роль в механике. Тело можно рассматривать как материальную точку, если его размеры малы по сравнению с расстоянием, которое оно проходит, или по сравнению с расстоянием от него до других тел.
Пример. Размеры орбитальной станции, находящейся на орбите около Земли, можно не учитывать, а рассчитывая траекторию движения космического корабля при стыковке со станцией, без учета ее размеров не обойтись.
Характеристики механического движения: перемещение, скорость, ускорение.
Механическое движение характеризуется тремя физическими величинами: перемещением, скоростью и ускорением.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют траекторией движения тела.
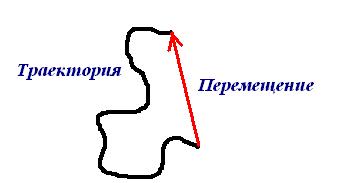
Линия, по которой движется точка тела, называется траекторией движения.
Длина траектории называется пройденным путем.
Обозначается l, измеряется в метрах. (траектория – след, путь – расстояние)
Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина.
Вектор, соединяющий начальную и конечную точки траектории, называется перемещением.
Обозначается S, измеряется в метрах.(перемещение – вектор, модуль перемещения – скаляр)
Скорость — векторная физическая величина, характеризующая быстроту перемещения тела, численно равная отношению перемещения за малый промежуток времени к величине этого промежутка.
Обозначается v
Формула скорости: 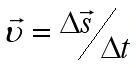 или
или 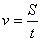
Единица измерения в СИ – м/с.
На практике используют единицу измерения скорости км/ч (36 км/ч = 10 м/с).
Измеряют скорость спидометром.
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле:
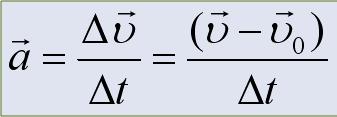
Ускорение измеряют акселерометром
Единица измерения в СИ м/с2
Таким образом, основными физическими величинами в кинематике материальной точки являются пройденный путь l, перемещение , скорость и ускорение . Путь l является скалярной величиной. Перемещение , скорость и ускорение – величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д.
Проверить свои знания (тест по теме «Механическое движение, его характеристики»)
Механи́ческим движе́нием тела называют изменение его положения в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики.
Раздел механики, описывающий геометрические свойства движения без учёта причин, его вызывающих, называется кинематикой.
В более общем значении движением называют изменение состояния физической системы с течением времени. Например, можно говорить о движении волны в среде.
Виды механического движения[править | править код]
Механическое движение можно рассматривать для разных механических объектов:
- Движение материальной точки полностью определяется изменением её координат во времени (например, для плоскости — изменением абсциссы и ординаты). Изучением этого занимается кинематика точки. В частности, важными характеристиками движения являются траектория материальной точки, перемещение, скорость и ускорение.
- Прямолинейное движение точки (когда она всегда находится на прямой, скорость параллельна этой прямой)
- Криволинейное движение — движение точки по траектории, не представляющей собою прямую, с произвольным ускорением и произвольной скоростью в любой момент времени (например, движение по окружности).
- Движение твёрдого тела складывается из движения какой-либо его точки (например, центра масс) и вращательного движения вокруг этой точки. Изучается кинематикой твёрдого тела.
- Если вращение отсутствует, то движение называется поступательным и полностью определяется движением выбранной точки. Движение при этом не обязательно является прямолинейным.
- Для описания вращательного движения — движения тела относительно выбранной точки, например закреплённого в точке, — используют Углы Эйлера. Их количество в случае трёхмерного пространства равно трём.
- Также для твёрдого тела выделяют плоское движение — движение, при котором траектории всех точек лежат в параллельных плоскостях, при этом оно полностью определяется одним из сечений тела, а сечение тела — положением любых двух точек.
- Движение сплошной среды. Здесь предполагается, что движение отдельных частиц среды довольно независимо друг от друга (обычно ограничено лишь условиями непрерывности полей скорости), поэтому число определяющих координат бесконечно (неизвестными становятся функции).
Геометрия движения[править | править код]
- По окружности (см. Первая космическая (круговая) скорость)
- По эллипсу
- По параболе (см. Вторая космическая (параболическая) скорость), под действием однородного гравитационного поля
- По гиперболе
- Равномерное движение
- Квадратриса
- Кривая погони. Эволюта (огибающая нормалей) трактрисы: (цепная линия, поверхность которой — катеноид)
- Под действием однородного гравитационного поля
- Кривая скорейшего спуска
Время спуска под действием только силы тяжести не зависит от расположения начальной точки на дуге циклоиды
- Лемниската Бернулли: материальная точка, движущаяся по кривой под действием однородного гравитационного поля, пробегает дугу за то же время, что и соответствующую хорду. При этом ось лемнискаты составляет угол с вектором напряжённости поля, а центр лемнискаты совпадает с исходным положением движущейся точки.
- Кривая скорейшего спуска
Относительность движения[править | править код]
Два стрелка неподвижны относительно друг друга, но движутся, если рассматривать другие системы отсчёта.
Относительность — зависимость механического движения тела от системы отсчёта. Система отсчёта представляет собой совокупность системы координат для определения положения тела в пространстве и часов для определения времени. Не указав систему отсчёта, не имеет смысла говорить о движении.
См. также[править | править код]
- Теория относительности
Ссылки[править | править код]
- Механическое движение (видео, программа 10 класса)
- Равномерное и неравномерное движение
Характеристики механического движения тела:
— траектория (линия, вдоль которой движется тело),
— перемещение (направленный отрезок прямой, соединяющий начальное положение тела M1 с его последующим положением M2),
— скорость (отношение перемещения ко времени движения — для равномерного движения).
Основные виды механического движения
В зависимости от траектории движение тела разделяются на:
— прямолинейные;
— криволинейные.
В зависимости от скорости движения разделяются на:
— равномерные,
— равноускоренные
— равнозамедленные
В зависимости от способа перемещения движения бывают:
— Поступательное
— Вращательное
— Колебательное
— Сложные движения (Например: винтовое движение, в котором тело равномерно вращается вокруг некоторой оси и в тоже время совершает вдоль этой оси равномерное поступательное движение)
Поступательное движение – это движение тела, при котором все его точки движутся одинаково. В поступательном движении всякая прямая, соединяющая любые две точки тела остается параллельной сама себе.
Вращательное движение – это движение тела вокруг некоторой оси. При таком движении все точки тела совершают движение по окружностям, центром которых является эта ось.
Колебательное движение – это периодическое движение, которое совершается поочерёдно в двух противоположных направлениях.
Например, колебательное движение совершает маятник в часах.
Поступательное и вращательное движения – самые простые виды механического движения.
Прямолинейным и равномерным движение называется такое движение, когда за любые сколь угодно малые равные промежутки времени тело совершает одинаковые перемещения. Запишем математическое выражение этого определения s = υ ? t. Это значит, что перемещение определяют по формуле, а координату — по формуле.
Равноускоренным движением называется движение тела, при котором его скорость за любые равные промежутки времени увеличивается одинаково. Для характеристики этого движения нужно знать скорость тела в данный момент времени или в данной точке траектории, т. е. мгновенную скорость, а также ускорение.
Мгновенная скорость — это отношение достаточно малого перемещения на участке траектории, примыкающей к этой точке, к малому промежутку времени, в течение которого это перемещение совершается.
υ = S/t. Единица измерения в системе СИ м/с.
Ускорение — величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло. α = ?υ/t (системе СИ м/с2) Иначе, ускорение — это быстрота изменения скорости или приращение скорости за каждую секунду α • t . Отсюда формула мгновенной скорости: υ = υ0 + α•t.
Перемещение при этом движении определяют по формуле: S = υ0 t + α • t2/2.
Равнозамедленным движением называется движение, когда ускорение имеет отрицательную величину, скорость при этом равномерно замедляется.
При равномерном движении по окружности углы поворота радиуса за любые равные промежутки времени будут одинаковы. Поэтому угловая скорость ω = 2πn, или ω = πN/30 ≈ 0.1N , где ω —уговая скорость n — число оборотов в секунду, N — число оборотов в минуту. ω в системе СИ измеряется в рад/с. (1/c)/ Она представляет угловую скорость, при которой каждая точка тела за одну секунду проходит путь, равный её расстоянию от оси вращения. При этом движении модуль скорости постоянный, он направлен по касательной к траектории и постоянно меняет направление (см. рис.), поэтому возникает центростремительное ускорение.
Период вращения Т = 1/n — это время,за которое тело совершает один полный оборот, поэтому ω = 2π/Т.
Линейная скорость при вращательном движении выражается формулами:
υ = ωr, υ = 2πrn, υ = 2πr/T, где r — расстояние точки от оси вращения. Линейная скорость точек, лежащих на окружности вала или шкива, называется окружной скоростью вала или шкива (в системе СИ м/с)
При равномерном движении по окружности скорость остается постоянной по величине но все время меняется по направлению. Всякое изменение скорости связано с ускорением. Ускорение изменяющее скорость по направлению называется нормальным или центростремительным, это ускорение перпендикулярно к траектории и направлено к центру ее кривизны (к центру окружности, если траектория окружность)
αп = υ2/R или αп = ω2R (так как υ = ωR где R радиус окружности, υ — скорость движения точки)
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта.
Положение тела (точки) в пространстве можно определить относительно какого-либо другого тела, выбранного за тело отсчета A. Тело отсчета, связанная с ним система координат и часы составляют систему отсчета. Характеристики механического движения относительны, т. е. они могут быть различными в разных системах отсчета.
Пример: за движением лодки следят два наблюдателя: один на берегу в точке O, другой — на плоту в точке O1 (см. рис.). Проведем мысленно через точку О систему координат XOY — это неподвижная система отсчета. Другую систему X’O’Y’ свяжем с плотом — это подвижная система координат. Относительно системы X’O’Y’ (плота) лодка за время t совершает перемещение и будет двигаться со скоростью υ = s лодки относительно плота /t v = (s лодки- s плота)/t. Относительно системы XOY (берег) лодка за это же время совершит перемещение s лодки, где s лодкиперемещение плота относительно берега. Скорость лодки относительно берега или . Скорость тела относительно неподвижной системы координат равна геометрической сумме скорости тела относительно подвижной системы и скорости этой системы относительно неподвижной.
Виды систем отсчёта могут быть различными, например, неподвижная система отсчёта, подвижная система отсчёта, инерциальная система отсчёта, неинерциальная система отсчёта.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 апреля 2020;
проверки требует 1 правка.
Враща́тельное движе́ние — вид механического движения. При вращательном движении материальная точка описывает окружность. При вращательном движении абсолютно твёрдого тела все его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.
При выборе некоторых осей вращения, можно получить сложное вращательное движение — сферическое движение, когда точки тела движутся по сферам. При вращении вокруг неподвижной оси, не проходящей через центр тела или вращающуюся материальную точку, вращательное движение называется круговым.
Основной закон динамики вращательного движения[править | править код]
Производная по времени от момента количества движения механической системы относительно неподвижной инерциальной системы отсчёта точки или центра инерции системы равна главному моменту относительно той же точки всех внешних сил, приложенных к системе.
Характеристики вращения тела[править | править код]
Кинематические характеристики[править | править код]
Вращение характеризуется углом , измеряющимся в градусах или радианах, угловой скоростью (измеряется в рад/с) и угловым ускорением (единица измерения — рад/с²).
При равномерном вращении ( — период вращения),
- Частота вращения — число оборотов в единицу времени.
- Линейная скорость точки, находящейся на расстоянии от оси вращения
- Угловая скорость вращения тела — аксиальный вектор (псевдовектор).
Динамические характеристики[править | править код]
Свойства твердого тела при его вращении описываются моментом инерции твёрдого тела. Эта характеристика входит в дифференциальные уравнения, полученные из уравнений Гамильтона или Лагранжа. Кинетическую энергию вращения можно записать в виде:
В этой формуле момент инерции играет роль массы, а угловая скорость — роль скорости. Момент инерции выражает геометрическое распределение массы в теле и может быть найден из формулы
- Момент инерции — физическая величина, мера инертности тела во вращательном движении. Характеризует распределение масс в теле. Различают осевой и центробежный момент инерции. Осевой момент инерции определяется равенством:
где — масса, — расстояние от -й точки до оси[1].
См. также[править | править код]
- Поступательное движение
- Плоскопараллельное движение
- Сложное движение
- Сферическое движение
Примечания[править | править код]
- ↑ Момент инерции // Физическая энциклопедия. В 5-ти томах / Главный редактор А. М. Прохоров. — М.: Советская энциклопедия, 1988.
Ссылки[править | править код]
- Бобылёв Д. К. Ось, в математике, механике и физике // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Вращение твердого тела. Открытая Физика 2.6. Часть I. «ФИЗИКОН». Дата обращения 23 января 2015.
- Джанибеков демонстрирует пример вращения абсолютно жесткого тела, закрученного вокруг оси, не совпадающей с осью наименьшего или наибольшего момента инерции
- Вращение твёрдых тел в невесомости вокруг разных осей
- Б. Яворский А. Детлаф, Физика, М.: Дрофа, 1998.
Физика для средней школы
Кинематика — раздел механики, изучающий движение тел без учета причин, вызвавших это движение.
Основной задачей кинематики является нахождение положения тела в любой момент времени, если известны его положение, скорость и ускорение в начальный момент времени.
Механическое движение — это изменение положения тел (или частей тела) относительно друг друга в пространстве с течением времени.
Для описания механического движения надо выбрать систему отсчета.
Тело отсчета — тело (или группа тел), принимаемое в данном случае за неподвижное, относительно которого рассматривается движение других тел.
Система отсчета — это система координат, связанная с телом отсчета, и выбранный способ измерения времени (рис. 1).
Рис. 1
Положение тела можно определить с помощью радиуса-вектора или с помощью координат.
Радиус-вектор точки — направленный отрезок прямой, соединяющий начало отсчета О с точкой (рис. 2).
Рис. 2
Координата x точки — это проекция конца радиуса-вектора точки на ось Ох. Обычно пользуются прямоугольной системой координат. В этом случае положение точки на линии, плоскости и в пространстве определяют соответственно одним (x), двумя (х, у) и тремя (х, у, z) числами — координатами (рис. 3).
Рис. 3
В элементарном курсе физики изучают кинематику движения материальной точки.
Материальная точка — тело, размерами которого в данных условиях можно пренебречь.
Этой моделью пользуются в тех случаях, когда линейные размеры рассматриваемых тел много меньше всех прочих расстояний в данной задаче или когда тело движется поступательно.
Поступательным называется движение тела, при котором прямая, проходящая через любые две точки тела, перемещается, оставаясь параллельной самой себе. При поступательном движении все точки тела описывают одинаковые траектории и в любой момент времени имеют одинаковые скорости и ускорения. Поэтому для описания такого движения тела достаточно описать движение его одной произвольной точки.
В дальнейшем под словом «тело» будем понимать «материальная точка».
Линия, которую описывает движущееся тело в определенной системе отсчета, называется траекторией. На практике форму траектории задают с помощью математических формул (y = f(x) — уравнение траектории) или изображают на рисунке. Вид траектории зависит от выбора системы отсчета. Например, траекторией тела, свободно падающего в вагоне, который движется равномерно и прямолинейно, является прямая вертикальная линия в системе отсчета, связанной с вагоном, и парабола в системе отсчета, связанной с Землей.
В зависимости от вида траектории различают прямолинейное и криволинейное движение.
Путь s — скалярная физическая величина, определяемая длиной траектории, описанной телом за некоторый промежуток времени. Путь всегда положителен: s > 0.
Перемещение тела за определенный промежуток времени — направленный отрезок прямой, соединяющий начальное (точка ) и конечное (точка М) положение тела (см. рис. 2):
,
где — радиусы-векторы тела в эти моменты времени.
Проекция перемещения на ось Ox
,
где — координаты тела в начальный и конечный моменты времени.
Модуль перемещения не может быть больше пути .
Знак равенства относится к случаю прямолинейного движения, если направление движения не изменяется.
Зная перемещение и начальное положение тела, можно найти его положение в момент времени t:
Скорость — мера механического состояния тела. Она характеризует быстроту изменения положения тела относительно данной системы отсчета и является векторной физической величиной.
Средняя скорость — векторная физическая величина, численно равная отношению перемещения к промежутку времени, за который оно произошло, и направленная вдоль перемещения (рис. 4):
Рис. 4
В СИ единицей скорости является метр в секунду (м/с).
Средняя скорость, найденная по этой формуле, характеризует движение только на том участке траектории, для которого она определена. На другом участке траектории она может быть другой.
Иногда пользуются средней скоростью пути
,
где s — путь, пройденный за промежуток времени . Средняя скорость пути — это скалярная величина.
Мгновенная скорость тела — скорость тела в данный момент времени (или в данной точке траектории). Она равна пределу, к которому стремится средняя скорость за бесконечно малый промежуток времени . Здесь — производная от радиуса-вектора по времени.
В проекции на ось Ох:
Мгновенная скорость тела направлена по касательной к траектории в каждой ее точке в сторону движения (см. рис. 4).
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. Оно показывает, на какую величину изменяется скорость тела за единицу времени.
Среднее ускорение — физическая величина, численно равная отношению изменения скорости ко времени, за которое оно произошло:
Вектор направлен параллельно вектору изменения скорости в сторону вогнутости траектории (рис. 5).
Рис. 5
Мгновенное ускорение:
В СИ единицей ускорения является метр на секунду в квадрате (м/с2).
В общем случае мгновенное ускорение направлено под углом к скорости. Зная траекторию, можно определить направление скорости, но не ускорения. Направление ускорения определяется направлением равнодействующей сил, действующих на тело.
При прямолинейном движении с возрастающей по модулю скоростью (рис. 6, а) векторы сонаправлены и проекция ускорения на направление движения положительна.
При прямолинейном движении с убывающей по модулю скоростью (рис. 6, б) направления векторов противоположны и проекция ускорения на направление движения отрицательна.
Рис. 6
Вектор при криволинейном движении можно разложить на две составляющие, направленные вдоль скорости и перпендикулярно скорости (рис. 7), — тангенциальное ускорение, характеризующее быстроту изменения модуля скорости при криволинейном движении, — нормальное ускорение, характеризующее быстроту изменения направления вектора скорости при криволинейном движении Модуль ускорения
Рис. 7
