Какое свойство материала характеризует модуль сдвига
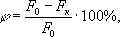
Если нарисовать круг Мора из центра системы координат, то получится особый частный случай плоского нагружения.
Из такого круга следует, что на площадках +- 45 градусов будут отсутствовать нормальные напряжения, а действующие касательные напряжения будут максимальны и равны главным напряжениям. Такой круг Мора является иллюстрацией следующего нагружения:
Тут действуют взаимно перпендикулярные нормальные напряжения; по одной оси – растягивающие, по другой – сжимающие, при этом напряжения эти численно равны.
Теперь в этом элементе выделим новый элемент, расположенный под углом 45 градусов:
Этот элемент abcd находится в равновесии под действием только касательных напряжений. Такое напряжённое состояние называется чистым сдвигом.
Рассмотрим деформацию элемента abcd.
Так как по граням этого элемента нормальные напряжения не действуют, то длины ab, ad, bc и cd не изменятся при деформации, но горизонтальная диагональ удлинится, а вертикальная диагональ ac укоротится, вследствие чего квадрат abcd превратится в ромб, как указано на рисунке пунктиром.
Угол при b, который до деформации был равен π/2, теперь становится меньше π/2, скажем, (π/2 — γ), и в то же время угол при a увеличивается и становится равным (π/2 + γ).
Малый угол γ определяет искажение элемента abcd и называется относительным сдвигом.
Для наглядности повернём и поместим элемент abcd в положение, как показано на рисунке ниже:
После его искажения касательными напряжениями он примет положение, указанное пунктиром. Так как, например, в металлах, относительные деформации крайне незначительны, то и здесь будет логично ожидать, что угол γ будет очень малым. Для очень малых углов тангенс угла равен самому углу, потому запишем:
Величина aa1 – это величина абсолютного сдвига, а величина ad – величина расстояния между сдвигающимися плоскостями. Соответственно, относительный сдвиг – это их отношение.
Если материал подчиняется закону Гука, то этот сдвиг будет пропорционален касательному напряжению и будет зависеть от механических свойств материала:
G – величина постоянная и характеризующая упругие характеристики материала. Называется эта величина модулем упругости при сдвиге или модулем сдвига.
Так как искажение элемента abcd вполне определяется из удлинения и укорочения его диагоналей, и так как эти деформации можно вычислить при помощи полученных ранее уравнений, то можно увидеть, что модуль G может быть выражен через модуль E и коэффициент Пуассона μ. Для установления этой зависимости рассмотрим треугольник Oab:
В нём:
Из треугольника Oa1b1 находим:
Для малого угла γ можно принять:
Помня, что в случае чистого сдвига:
Следовательно:
Откуда:
Отсюда:
То есть модуль сдвига для изотропного материала можно легко вычислить, если знать модуль Юнга и коэффициент Пуассона.
Так как модуль сдвига имеет ту же размерность, что и напряжение, то ему можно дать определение, как фиктивному касательному напряжению, при котором величина абсолютного сдвига будет равна расстоянию между сдвигаемыми плоскостями. Но так как, например, в металлах сдвиговые деформации крайне незначительны, то и модуль сдвига крайне велик относительно действующих напряжений.
Модуль сдвига – это величина, характеризующая упругие свойства данного материала, наравне с модулем Юнга и коэффициентом Пуассона. Для изотропных материалов достаточно знать две величины, чтобы получить третью (вывод зависимости между ними был только что показан), однако же в общем случае (для материалов с различными, в зависимости от направления, свойствами) эти три величины могут различаться в зависимости от ориентации.
Важно понимать, что опыт на сдвиг гораздо сложнее опыта на растяжения в плане доступности для проведения. В частности, очень тяжело приложить сдвиговые силы так, чтобы распределение касательных напряжений было равномерным.
Поэтому состояние чистого сдвига обычно получают путём кручения цилиндрической трубы:
(Кручение будет рассмотрено в одном из следующих модулей)
Важно понимать и обратную ситуацию, когда какой-то элемент находится в состоянии сдвига, например, при том же кручении, то можно поворотом этого элемента на 45 градусов прийти к двухосному нагружению (растяжению в одном направлении и сжатию в другом). Такая ситуация очень часто встречается на практике, и мы с этим столкнёмся как в изгибе, так и в кручении.
Закон Гука для сдвига в относительной форме:
Закон Гука для сдвига в абсолютной форме:
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 10 января 2018;
проверки требуют 8 правок.
Модуль упругости — общее название нескольких физических величин, характеризующих способность твёрдого тела (материала, вещества) упруго деформироваться (то есть не постоянно) при приложении к нему силы. В области упругой деформации модуль упругости тела в общем случае зависит от напряжения и определяется производной (градиентом) зависимости напряжения от деформации, то есть тангенсом угла наклона начального линейного участка диаграммы напряжений-деформаций:
где:
В наиболее распространенном случае зависимость напряжения и деформации линейная (закон Гука):
.
Если напряжение измеряется в паскалях, то, поскольку деформация является безразмерной величиной, единицей измерения Е также будет паскаль. Альтернативным определением является определение, что модуль упругости — это напряжение, достаточное для того, чтобы вызвать увеличение длины образца в два раза. Такое определение не является точным для большинства материалов, потому что это значение намного больше чем предел текучести материала или значения, при котором удлинение становится нелинейным, однако оно может оказаться более интуитивным.
Разнообразие способов, которыми могут быть изменены напряжения и деформации, включая различные направления действия силы, позволяют определить множество типов модулей упругости. Здесь даны три основных модуля:
- Модуль Юнга (E) характеризует сопротивление материала растяжению/сжатию при упругой деформации, или свойство объекта деформироваться вдоль оси при воздействии силы вдоль этой оси; определяется как отношение напряжения к деформации сжатия (удлинения). Часто модуль Юнга называют просто модулем упругости.
- Модуль сдвига или модуль жесткости (G или ) характеризует способность материала сопротивляться изменению формы при сохранении его объёма; он определяется как отношение напряжения сдвига к деформации сдвига, определяемой как изменение прямого угла между плоскостями, по которым действуют касательные напряжения. Модуль сдвига является одной из составляющих явления вязкости.
- Модуль объёмной упругости или Модуль объёмного сжатия (K) характеризует способность объекта изменять свой объём под воздействием всестороннего нормального напряжения (объёмного напряжения), одинакового по всем направлениям (возникающего, например, при гидростатическом давлении). Он равен отношению величины объёмного напряжения к величине относительного объёмного сжатия. В отличие от двух предыдущих величин, модуль объёмной упругости невязкой жидкости отличен от нуля (для несжимаемой жидкости — бесконечен).
Существуют и другие модули упругости: коэффициент Пуассона, параметры Ламе.
Гомогенные и изотропные материалы (твердые), обладающие линейными упругими свойствами, полностью описываются двумя модулями упругости, представляющими собой пару любых модулей. Если дана пара модулей упругости, все другие модули могут быть получены по формулам, представленным в таблице ниже.
В невязких течениях не существует сдвигового напряжения, поэтому сдвиговый модуль всегда равен нулю. Это влечёт также и равенство нулю модуля Юнга.
Модули упругости (Е) для некоторых веществ:
| Материал | Е, МПа | Е, кгс/см² |
|---|---|---|
| Алюминий | 70000 | 713 800 |
| Вода | 2030 | 20300 |
| Дерево | 10000 | 102 000 |
| Кость | 30000 | 305 900 |
| Медь | 100000 | 1 020 000 |
| Резина | 5 | 50 |
| Сталь | 200000 | 2 039 400 |
| Стекло | 70000 | 713 800 |
См. также[править | править код]
- Модуль Юнга
- Модуль сдвига G
- Жёсткость
- Предел текучести
- Упругость
- Предел прочности
- Упругие волны
- Уравнение Гассмана
- en:Dynamic modulus
Ссылки[править | править код]
- Free database of engineering properties for over 63,000 materials
- Расчёт модуля упругости по ПНАЭ Г-7-002-86
- Иомдина Е. Н. Механические свойства тканей глаза человека. (недоступная ссылка)
Литература[править | править код]
- Модули упругости // Большая Советская энциклопедия (в 30 т.) / А. М. Прохоров (гл. ред.). — 3-е изд. — М.: Сов. энциклопедия, 1974. — Т. XVI. — С. 406. — 616 с.
- G. Mavko, T. Mukerji, J. Dvorkin. The Rock Physics Handbook. Cambridge University Press 2003 (paperback). ISBN 0-521-54344-4
46.Основные
механические свойства. Модуль сдвига
Механические
свойства материалов,
совокупность
показателей, характеризующих сопротивление
материала воз действующей на него
нагрузке, его способность деформироваться
при этом, а также особенности его
поведения в процессе разрушения. В
соответствии с этим М. с. м. измеряют
напряжениями (обычно
в кгс/мм2 или Мн/м2), деформациями
(в %), удельной работой деформации и
разрушения (обычно
в кгс×м/см2 или Мдж/м2), скоростью
развития процесса разрушения при
статической или повторной нагрузке
(чаще всего в мм за
1 сек или
за 1000 циклов повторений нагрузки, мм/кцикл). М.
с. м. определяются при механических
испытаниях образцов различной формы.
В
общем случае материалы в конструкциях
могут подвергаться самым различным по
характеру нагрузкам (рис.
1):
работать нарастяжение,
сжатие, изгиб, кручение,
срез и т. д. или подвергаться совместному
действию нескольких видов нагрузки,
например растяжению и изгибу. Также
разнообразны условия эксплуатации
материалов и по температуре, окружающей
среде, скорости приложения нагрузки и
закону её изменения во времени. В
соответствии с этим имеется много
показателей М. с. м. и много методов
механических испытаний. Для металлов
и конструкционных пластмасс наиболее
распространены испытания на
растяжение, твёрдость,
ударный изгиб; хрупкие конструкционные
материалы (например, керамику,
металлокерамику) часто испытывают на
сжатие и статический изгиб; механические
свойства композиционных материалов
важно оценивать, кроме того, при
испытаниях на сдвиг.
Диаграмма
деформации. Приложенная
к образцу нагрузка вызывает его деформацию.
Соотношения между нагрузкой и деформацией
описываются т. н. диаграммой деформации
(рис.
2).
Вначале деформация образца (при
растяжении — приращение длины Dl )
пропорциональна возрастающей нагрузке Р,
затем в точке n эта
пропорциональность нарушается, однако
для увеличения деформации необходимо
дальнейшее повышение нагрузки Р;
при Dl >
Dlв деформация
развивается без приложения усилия
извне, при постепенно падающей нагрузке.
Вид диаграммы деформации не меняется,
если по оси ординат откладывать
напряжение
![]()
а
по оси абсцисс — относительное удлинение
![]()
(F и l —
соответственно начальная площадь
поперечного сечения и расчётная длина
образца).
Сопротивление
материалов измеряется напряжениями,
характеризующими нагрузку, приходящуюся
на единицу площади поперечного сечения
образца
![]()
в кгс/мм2. Напряжение
![]()
при
котором нарушается пропорциональный
нагрузке рост деформации, называется
пределом пропорциональности. При
нагрузкеР < Рn разгрузка
образца приводит к исчезновению
деформации, возникшей в нём под действием
приложенного усилия; такая деформация
называется упругой. Небольшое превышение
нагрузки относительно Рn может
не изменить характера деформации —
она по-прежнему сохранит упругий
характер. Наибольшая нагрузка, которую
выдерживает образец без появления
остаточной пластической деформации
при разгрузке, определяет предел
упругости материала:
![]()
У
конструкционных неметаллический
материалов (пластмассы, резины)
приложенная нагрузка может вызвать
упругую, высокоэластическую и остаточную
деформации. В отличие от упругой,
высокоэластическая деформация исчезает
не сразу после разгрузки, а с течением
времени. Высокопрочные армированные
полимеры (стеклопластики, углепластики
и др.) разрушаются при удлинении 1—3%.
На последних стадиях нагружения у
некоторых армированных полимеров
появляется высокоэластическая
деформация. Высокоэластический модуль
ниже модуля упругости, поэтому диаграмма
деформации в этом случае имеет тенденцию
отклоняться к оси абсцисс.
Упругие
свойства. В
упругой области напряжение и деформация
связаны коэффициентом пропорциональности.
При растяжении s = Еd, где Е —
т. н. модуль нормальной упругости,
численно равный тангенсу угла наклона
прямолинейного участка кривой s = s(d) к
оси деформации (рис.
2).
При испытании на растяжение цилиндрического
или плоского образца одноосному (s1>0;
(s2 =
s3 =
0) напряжённому состоянию соответствует
трёхосное деформированное состояние
(приращение длины в направлении действия
приложенных сил и уменьшение линейных
размеров в двух других взаимно
перпендикулярных направлениях): d1>0;
d2 =
d3 <
0. Соотношение между поперечной и
продольной деформацией (коэффициент
Пуассона)
![]()
в
пределах упругости для основных
конструкционных материалов колеблется
в довольно узких пределах (0,27—0,3 для
сталей, 0,3—0,33 для алюминиевых сплавов).
Коэффициент Пуассона является одной
из основных расчётных характеристик.
Зная m и Е,
можно расчётным путём определить и
модуль сдвига
![]()
и
модуль объёмной упругости
![]()
Для
определения Е,
G,
и m пользуются тензометрами.
Сопротивление
пластической деформации. При
нагрузках Р > Рв наряду
со всё возрастающей упругой деформацией
появляется заметная необратимая, не
исчезающая при разгрузке пластическая
деформация. Напряжение, при котором
остаточная относительная деформация
(при растяжении — удлинение) достигает
заданной величины (по ГОСТ — 0,2 %),
называется условным пределом текучести
и обозначается
![]()
Практически
точность современных методов испытания
такова, что sп и
sе определяют
с заданными допусками соответственно
на отклонение от закона пропорциональности
[увеличение ctg(90 — a) на 25—50 %] и на величину
остаточной деформации (0,003—0,05 %) и
говорят об условных пределах
пропорциональности и упругости. Кривая
растяжения конструкционных металлов
может иметь максимум (точка в на рис.
2)
или обрываться при достижении наибольшей
нагрузки Рв’.
Отношение
![]()
характеризует
временное сопротивление (предел
прочности) материала. При наличии
максимума на кривой растяжения в области
нагрузок, лежащих на кривой левее в,
образец деформируется равномерно по
всей расчётной длине l0,
постепенно уменьшаясь в диаметре, но
сохраняя начальную цилиндрическую или
призматическую форму. При пластической
деформации металлы упрочняются, поэтому,
несмотря на уменьшение сечения образца,
для дальнейшей деформации требуется
прикладывать всё возрастающую нагрузку.
sв,
как и условные s0,2,
sn и
sе,
характеризует сопротивление металлов
пластической деформации. На участке
диаграммы деформации правее в форма
растягиваемого образца изменяется:
наступает период сосредоточенной
деформации, выражающейся в появлении
«шейки». Уменьшение сечения в шейке
«обгоняет» упрочнение металлов,
что и обусловливает падение внешней
нагрузки на участке Рв —
Pk.
У
многих конструкционных материалов
сопротивление пластической деформации
в упруго-пластической области при
растяжении и сжатии практически
одинаково. Для некоторых металлов и
сплавов (например, магниевые сплавы,
высокопрочные стали) характерны заметные
различия по этой характеристике при
растяжении и сжатии. Сопротивление
пластической деформации особенно часто
(при контроле качества продукции,
стандартности режимов термической
обработки и в др. случаях) оценивается
по результатам испытаний на твёрдость
путём вдавливания твёрдого наконечника
в форме шарика (твёрдость по Бринеллю
или Роквеллу), конуса (твёрдость по
Роквеллу) или пирамиды (твёрдость по
Виккерсу). Испытания на твёрдость не
требуют нарушения целостности детали
и потому являются самым массовым
средством контроля механических
свойств. Твёрдость по Бринеллю (HB) при
вдавливании шарика диаметром D под
нагрузкой Р характеризует
среднее сжимающее напряжение, условно
вычисляемое на единицу поверхности
шарового отпечатка диаметром d:
![]()
Характеристики
пластичности. Пластичность
при растяжении конструкционных
материалов оценивается удлинением
![]()
или
сужением
![]()
при
сжатии — укорочением
![]()
(где h и hk —
начальная и конечная высота образца),
при кручении — предельным углом
закручивания рабочей части образца
Q,рад или
относительным сдвигом g = Qr (где r —
радиус образца). Конечная ордината
диаграммы деформации (точка k на рис.
2)
характеризует сопротивление разрушению
металла Sk,
которое определяется
![]()
(Fk —
фактическая площадь в месте разрыва).
Модуль
сдвига-величина,
характеризующая деформацию сдвига.
Модуль
сдвига равен отношению касательного
напряжения к величине угла сдвига.
 В начальной
В начальной
части диаграмма сдвига (на рисунке)
линейная, т.е. угол сдвига пропорционален
касательному напряжению .
Закон пропорциональности, называемый
законом Гука при сдвиге, может быть
записан:
![]()
где
коэффициент пропорциональности G называется
модулем сдвига сдвига или модулем
упругости 2-го рода. Он характеризует
сопротивление материала упругим
деформациям и является его упругой
постоянной.
| Модуль сдвига | |
|---|---|
Общие символы | G , S |
| единица СИ | паскаль |
Дифференцирования от | G = τ / γ |
В науке материалов , модуль сдвига или модулем жесткости , обозначаемой G , или иногда S или ц , определяется как отношение напряжения сдвига к деформации сдвига :
где
= Напряжение сдвига
это сила, которая действует
это область, на которой сила действует
= Деформации сдвига. В технике , в другом месте
это поперечное смещение
начальная длина
Полученный СИ единица модуля сдвига является паскалем (Па), хотя это обычно выражается в гигапаскаль (ГП) или в тысячах фунтов на квадратный дюйм (кг на квадратный дюйм) . Ее мерная форма есть М 1 л -1 Т -2 , заменив силы на массы раз ускорения .
объяснение
Модуль сдвига является одной из нескольких величин для измерения жесткости материалов. Все они возникают в обобщенном законе Гука :
- Модуль Юнга Е описывает реакцию деформации материала к одноосной деформации в направлении этого напряжения (например , потянув за концы проволоки или положить вес на верхнюю часть колонки, с проволокой , получить больше и колонку потери высоты),
- в коэффициент Пуассона ν описывает отклик в направлениях , ортогональных к этому одноосного напряжения (провод становится тоньше и толще столбец),
- объемный модуль упругости К описывает реакцию материала к (однородной) гидростатического давления (например , давление на дне океана или глубокий бассейн),
- модуль сдвига G описывает отклик материала на напряжение сдвига (как резка его с тупыми ножницами).
- Эти модули не являются независимыми, и для изотропных материалов они связаны через уравнение .
Модуль сдвига связан с деформацией твердого тела , когда он испытывает усилие параллельно одной из его поверхностей , а ее противоположная поверхность испытывает противодействующую силу (например, трение). В случае объекта формы , как прямоугольная призма, он будет деформироваться в параллелепипед . Анизотропные материалы , такие как древесины , бумаги , а также по существу всех кристаллов обладают одного различной реакцию на стресс материала или деформации при испытании в разных направлениях. В этом случае, один , возможно , потребуется использовать полный тензор-выражение упругих констант, а не одно скалярное значение.
Одним из возможного определения жидкости будет материалом с нулевым модулем сдвига.
волны
Влияния выбранных добавок стекла компонентов на модуль сдвига конкретного базового стекла.
В однородных и изотропных твердых телах, существует два вида волн, волны давления и сдвиговых волн . Скорость волны сдвига, управляются модулем сдвига,
где
G представляет собой модуль сдвига
телесная — й плотность .
Модуль сдвига металлов
Модуль сдвига меди в зависимости от температуры. Экспериментальные данные приведены с цветными символами.
Модуль сдвига металлов, как правило, наблюдается уменьшение с ростом температуры. При высоких давлениях, модуль сдвига также, как представляется, возрастает с увеличением приложенного давления. Корреляция между температурой плавления, энергией образования вакансий и модулем сдвига наблюдались во многих металлах.
Несколько моделей существуют, что попытка предсказать модуль сдвига металлов (и, возможно, что сплавы). Shear модель модуля упругости, которые были использованы в пластиковых вычислениях потока включает в себя:
- модель модуля сдвига МТС разработана и использован в сочетании с механическим Пороговым усилием модели напряжения пластического течения (МТС).
- Стейнберг-Кокрэн-Гуинан (СКГ) Модель модуля сдвига разработана и использован в сочетании с Steinberg-Cochran-Гуинан-Лунд (SCGL) поток модели стресса.
- Надаль и LePoac (NP) , модуль упругости при сдвиге модель , которая использует теорию Lindemann для определения зависимости температуры и модели SCG для зависимости давления от модуля сдвига.
Модель модуля сдвига МТС
Модель модуля сдвига МТС имеет вид:
где представляет собой модуль сдвига при , а и материальные константы.
Модель модуля сдвига СКГ
Steinberg-Кокрэн-Гуинан (СКГ) Модель модуля сдвига зависит от давления и имеет вид
где ц 0 модуль сдвига в опорном состоянии ( Т = 300 К, р = 0, η = 1), р представляет собой давление, а Т представляет собой температуру.
Модель NP модуля сдвига
Надаль-Ле Poac (НП) Модель модуля сдвига представляет собой модифицированный вариант модели SCG. Эмпирическая температурная зависимость модуля сдвига в модели SCG заменяется уравнением на основе теории плавления Lindemann . Модель модуля сдвига НП имеет вид:
где
и μ 0 является модулем сдвига при 0 К и давлении окружающей среды, ζ представляет собой материал , параметр, к б является постоянной Больцмана , т является атомной массой , а е является постоянная Линдеманном .
Смотрите также
- Динамический модуль упругости
- Импульсное возбуждение
- Предел прочности на сдвиг
- Сейсмический момент
