Какое свойство лучей называются обратимостью

1. Главная
2. Вопросы & Ответы
3. Вопрос 6590183

Лучший ответ:

Другие вопросы:

Физика
8 класс

Вам уже известно, что свет от источника или от освещенного тела воспринимается человеком, если лучи света попадают в глаза. Как будет вести себя свет, если на его пути имеется преграда? Чтобы узнать это, проделаем следующий опыт.

От источника S направим через щель пучок света на экран. Экран будет освещен, но между источником и экраном мы ничего не увидим (рис. 134, а). Теперь между источником и экраном разместим какой-либо предмет: руку, листок бумаги. В этом случае излучение, достигнув поверхности предмета, отражается, изменяет своё направление и попадает в наши глаза, т. е. он становится виден.

Рис. 134. Падение лучей света на экран

Если запылить воздух между экраном и источником света, то становится видимым весь пучок света (рис. 134, б). Пылинки отражают свет и направляют его в глаза наблюдателя.

Это явление часто наблюдается, когда лучи солнца проникают в запылённый воздух комнаты.

Известно, что в солнечный день при помощи зеркала можно получить световой «зайчик» на стене, полу, потолке. Объясняется это тем, что пучок света, падая на зеркало, отражается от него, т. е. изменяет своё направление. Световой «зайчик» — это след отражённого пучка света на каком-либо экране. На рисунке 135 показано отражение света от зеркальной поверхности.

Рис. 135. Отражение света от зеркальной поверхности

Линия MN — поверхность раздела двух сред (воздух, зеркало). На эту поверхность из точки S падает пучок света. Его направление задано лучом SO. Направление отражённого пучка показано лучом ОВ. Луч SO — падающий луч, луч ОВ — отражённый луч. Из точки падения луча О проведён перпендикуляр ОС к поверхности MN. Угол SOC, образованный падающим лучом SO и перпендикуляром, называется углом падения (α). Угол СОВ, образованный тем же перпендикуляром ОС и отражённым лучом, называется углом отражения (β).

При изменении угла падения луча будет меняться и угол отражения. Это явление удобно наблюдать на специальном приборе (рис. 136). Прибор представляет собой диск на подставке. На диск нанесена круговая шкала с ценой деления 10°. По краю диска можно передвигать осветитель, дающий узкий пучок света. Закрепим в центре диска зеркальную пластинку и направим на неё пучок света (см. рис. 136).

Рис. 136. Прибор для наблюдения изменения угла падения света

Если пучок света падает под углом 45°, то под таким же углом он и отражается от зеркала. Передвигая осветитель по краю диска, будем менять угол падения луча и каждый раз отмечать соответствующий ему угол отражения. Во всех случаях угол отражения равен углу падения луча. При этом лучи отражённый и падающий лежат в одной плоскости с перпендикуляром, проведённым к зеркалу в точке падения луча. Таким образом, отражение света происходит по следующему закону: лучи падающий и отражённый лежат в одной плоскости с перпендикуляром, проведённым к границе раздела двух сред в точке падения луча.

Угол падения α равен углу отражения β.

∠ α = ∠ β.

Если луч падает на зеркало в направлении ВО (см. рис. 135), то отражённый луч пойдёт в направлении OS. Следовательно, падающий и отражённый лучи могут меняться местами. Это свойство лучей (падающего и отражённого) называется обратимостью световых лучей.

Всякая незеркальная, т. е. шероховатая, негладкая, поверхность рассеивает свет, так как на ней имеются небольшие выступы и углубления.

Такую поверхность можно представить в виде целого ряда малых плоских поверхностей, расположенных под разными углами друг к другу. Поэтому падающий на такую поверхность свет отражается по разным направлениям.

Вопросы

1. Пользуясь рисунком 135, расскажите содержание опытов, на основании которых были установлены законы отражения света.
2. Какой угол называют углом падения; углом отражения?
3. Сформулируйте законы отражения света.
4. Какое свойство лучей называется обратимостью?

Упражнение 45

1. Угол падения луча на зеркало равен 45°. Начертите отражённый луч. На этом же чертеже покажите расположение лучей для случая, когда угол падения равен 60°.
2. Угол падения луча на зеркало равен 0°. Чему равен угол отражения?
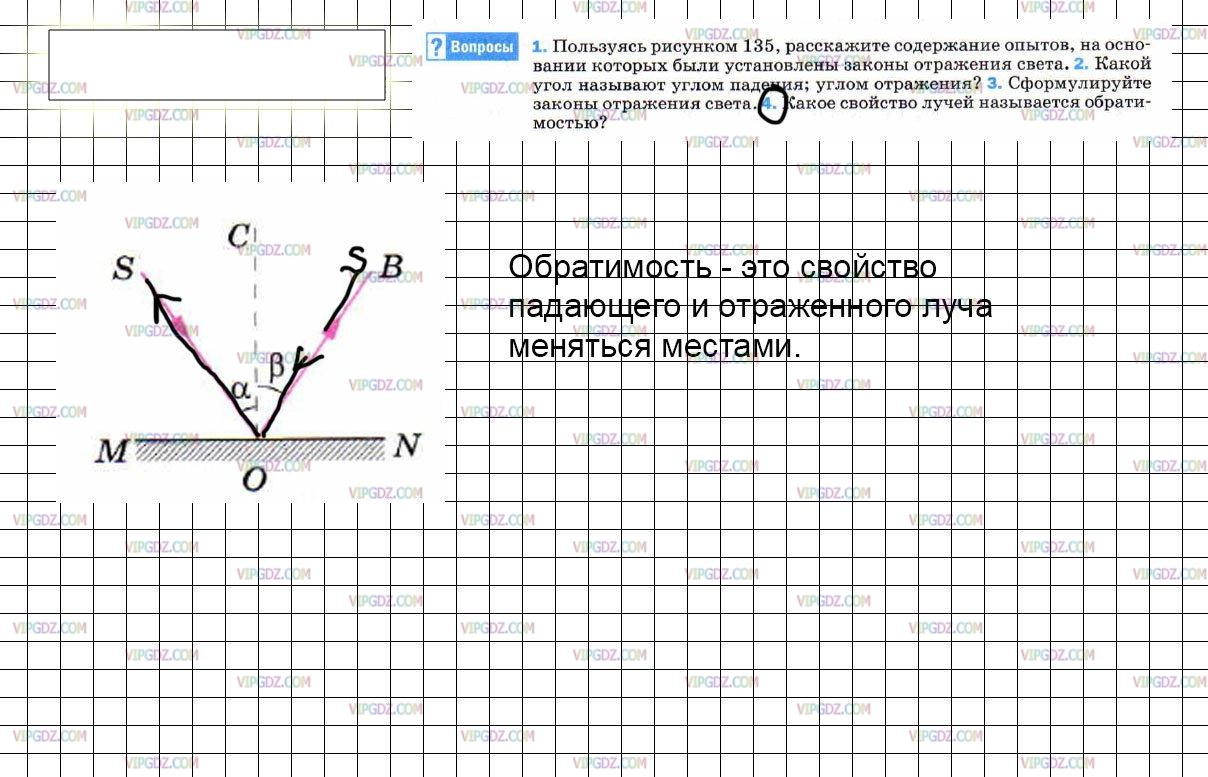
3. Перечертите в тетрадь рисунок 137. Постройте для каждого случая положение отражённого или падающего луча.

   

   Рис. 137

4. Высота солнца такова, что его лучи составляют с горизонтом угол 40°. Сделайте чертёж (рис. 138) и покажите на нём, как нужно расположить зеркало АВ, чтобы «зайчик» попал на дно колодца.

   

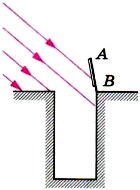
   Рис. 138

Глава 4. Световые явления

Вам уже известно, что свет от источника или от освещённого тела воспринимается человеком, если лучи света попадают в глаза. Как будет вести себя свет, если на его пути имеется преграда? Чтобы узнать это, проделаем следующий опыт.

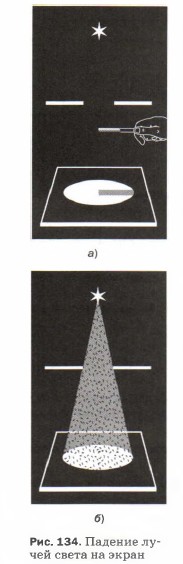
От источника S направим через щель пучок света на экран. Экран будет освещён, но между источником и экраном мы ничего не увидим (рис. 134, а). Теперь между источником и экраном разместим какой-либо предмет: руку, листок бумаги. В этом случае излучение, достигнув поверхности предмета, отражается, изменяет своё направление и попадает в наши глаза, т. е. он становится виден.

Если запылить воздух между экраном и источником света, то становится видимым весь пучок света (рис. 134, б). Пылинки отражают свет и направляют его в глаза наблюдателя.

Это явление часто наблюдается, когда лучи солнца проникают в запылённый воздух комнаты.

Известно, что в солнечный день при помощи зеркала можно получить световой «зайчик» на стене, полу, потолке. Объясняется это тем, что пучок света, падая на зеркало, отражается от него, т. е. изменяет своё направление. Световой «зайчик» — это след отражённого пучка света на каком-либо экране. На рисунке 135 показано отражение света от зеркальной поверхности.

Линия MN — поверхность раздела двух сред (воздух, зеркало). На эту поверхность из точки S падает пучок света. Его направление задано лучом SO. Направление отражённого пучка показано лучом ОB. Луч SO — падающий луч, луч ОB — отражённый луч. Из точки падения луча О проведён перпендикуляр ОС к поверхности MN. Угол SOC, образованный падающим лучом SO и перпендикуляром, называется углом падения (α). Угол СОВ, образованный тем же перпендикуляром ОС и отражённым лучом, называется углом отражения (β).

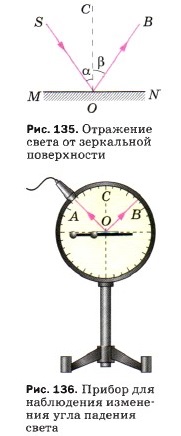
При изменении угла падения луча будет меняться и угол отражения. Это явление удобно наблюдать на специальном приборе (рис. 136). Прибор представляет собой диск на подставке. На диск нанесена круговая шкала с ценой деления 10°. По краю диска можно передвигать осветитель, дающий узкий пучок света. Закрепим в центре диска зеркальную пластинку и направим на неё пучок света (см. рис. 136). Если пучок света падает под углом 45°, то под таким же углом он и отражается от зеркала. Передвигая осветитель по краю диска, будем менять угол падения луча и каждый раз отмечать соответствующий ему угол отражения. Во всех случаях угол отражения равен углу падения луча. При этом лучи отражённый и падающий лежат в одной плоскости с перпендикуляром, проведённым к зеркалу в точке падения луча. Таким образом, отражение света происходит по следующему закону: лучи падающий и отражённый лежат в одной плоскости с перпендикуляром, проведённым к границе раздела двух сред в точке падения луча.

Угол падения α равен углу отражения β.

∠ α = ∠ β.

Если луч падает на зеркало в направлении ВО (см. рис. 135), то отражённый луч пойдёт в направлении OS. Следовательно, падающий и отражённый лучи могут меняться местами. Это свойство лучей (падающего и отражённого) называется обратимостью световых лучей.

Всякая незеркальная, т. е. шероховатая, негладкая, поверхность рассеивает свет, так как на ней имеются небольшие выступы и углубления.

Такую поверхность можно представить в виде целого ряда малых плоских поверхностей, расположенных под разными углами друг к другу. Поэтому падающий на такую поверхность свет отражается по разным направлениям.

Вопросы

1. Пользуясь рисунком 135, расскажите содержание опытов, на основании которых были установлены законы отражения света.
2. Какой угол называют углом падения; углом отражения? Сформулируйте законы отражения света. 4 Какое свойство лучей называется обратимостью?

Упражнение 45

1. Угол падения луча на зеркало равен 45°. Начертите отражённый луч. На этом же чертеже покажите расположение лучей для случая, когда угол падения равен 60°.

2. Угол падения луча на зеркало равен 0°. Чему равен угол отражения?

3. Перечертите в тетрадь рисунок 137. Постройте для каждого случая положение отражённого или падающего луча.

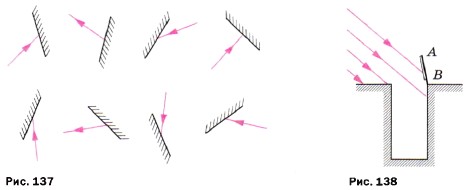
4. Высота солнца такова, что его лучи составляют с горизонтом угол 40°. Сделайте чертёж (рис. 138) и покажите на нём, как нужно расположить зеркало АВ, чтобы «зайчик» попал на дно колодца.