Какое свойство лапласа отражает что умножение аргумента оригинала

Содержание
Обнаружили ошибку?
Выделите ее мышью
и нажмите
Преобразование Лапласа как разложение сигнала по системе затухающих комплексных экспонент
Ранее мы рассмотрели преобразование Фурье сигнала  :
:

(1)
где  — спектральная плотность сигнала
— спектральная плотность сигнала  ,
,
 и
и  — операторы
— операторы
прямого и обратного преобразования Фурье соответственно.
Условием существования преобразования Фурье является абсолютная интегрируемость [1] исходного сигнала сигнала  , т.е. сходимость интеграла:
, т.е. сходимость интеграла:

(2)
При рассмотрении преобразования Фурье предполагается, что время  измеряется от минус бесконечности до плюс бесконечности. Кроме того (2) сужает класс сигналов, для которых существует преобразование Фурье.
измеряется от минус бесконечности до плюс бесконечности. Кроме того (2) сужает класс сигналов, для которых существует преобразование Фурье.
С другой стороны, все физические процессы имеют начало, поэтому мы можем считать, что исходный сигнал  определён на положительном интервале времени, т.е
определён на положительном интервале времени, т.е  , при
, при  .
.
Для того, чтобы предотвратить расхождение интеграла (2) умножим входной сигнал  на
на  , где
, где  — вещественная величина.
— вещественная величина.
Рассмотрим преобразование Фурье  полученного сигнала:
полученного сигнала:

(3)
Очевидно,  зависит от параметра
зависит от параметра  . Тогда
. Тогда  можно трактовать как функцию двух вещественных переменных
можно трактовать как функцию двух вещественных переменных  или как функцию одной комплексной переменной
или как функцию одной комплексной переменной  . Обозначив
. Обозначив  получим:
получим:

(4)
Выражение (4) представляет собой разложение  по системе затухающих комплексных экспонент
по системе затухающих комплексных экспонент  , которое носит название преобразования Лапласа, где
, которое носит название преобразования Лапласа, где  — оператор преобразования.
— оператор преобразования.
Исходный сигнал  называют оригиналом, а
называют оригиналом, а  — образом, или изображением оригинала.
— образом, или изображением оригинала.
Обратное преобразование Лапласа
Обратное преобразование Фурье (3) от  имеет вид:
имеет вид:

(5)
Умножим левую и правую части (5) на  , получим:
, получим:

(6)
Учтём, что  , изменим переменную интегрирования с
, изменим переменную интегрирования с  на
на  :
:

(7)
При этом верхний и нижний пределы интегрирования равны:

(8)
Окончательно (6) с учётом 7 и (8):

(9)
Выражение (9) определяет обратное преобразование Лапласа, которое обозначается оператором  .
.
Некоторые свойства преобразования Лапласа
Свойство линейности
Пусть сигнал  . Тогда преобразование Лапласа
. Тогда преобразование Лапласа  :
:

(10)
Следствием (10) является умножение на константу:

(11)
Свойство подобия (масштабирование по аргументу)
Пусть сигнал  имеет образ
имеет образ  . Тогда изображение масштабированного во времени сигнала
. Тогда изображение масштабированного во времени сигнала  равно:
равно:

(12)
Аналогично можно показать [2], что масштабирование образа по аргументу  приводит к оригиналу вида:
приводит к оригиналу вида:

(13)
Преобразование Лапласа задержанного сигнала
Рассмотрим преобразование Лапласа сигнала  , задержанного во времени на положительную величину
, задержанного во времени на положительную величину  .
.

(14)
Важно отметить, что (14) справедливо, если задержка  положительна, как это показано на рисунке 1.
положительна, как это показано на рисунке 1.

Рисунок 1. Пример положительной и отрицательной
задержки сигнала
Если же задержка отрицательна, то [2, стр. 40–41]:

(15)
Аналогичное свойство смещения образа:

(16)
Таким образом, смещение образа  на произвольное комплексное
на произвольное комплексное  приводит к умножению сигнала на
приводит к умножению сигнала на  .
.
Свойство дифференцирования оригинала и образа
Пусть дан сигнал  и его преобразование Лапласа равно
и его преобразование Лапласа равно  . Рассмотрим преобразование Лапласа производной сигнала
. Рассмотрим преобразование Лапласа производной сигнала  :
:

(17)
Применяя правило интегрирования по частям [3, стр. 330]:

(18)
где  — значение сигнала при
— значение сигнала при  . Если функция
. Если функция  при
при  имеет разрыв, то вместо
имеет разрыв, то вместо  необходимо брать правый предел
необходимо брать правый предел  :
:

(19)
при стремлении  к нулю справа.
к нулю справа.
Таким образом, использование аппарата преобразования Лапласа позволяет заменить дифференцирование умножением образа на переменную  . Это важнейшее свойство дало возможность перейти от дифференциальных уравнений при анализе цепей переменного тока к алгебраическим и использовать всю мощь аппарата операционного исчисления и теории функций комплексного переменного для синтеза и анализа электрических цепей.
. Это важнейшее свойство дало возможность перейти от дифференциальных уравнений при анализе цепей переменного тока к алгебраическим и использовать всю мощь аппарата операционного исчисления и теории функций комплексного переменного для синтеза и анализа электрических цепей.
Приведем также выражение для обратного преобразования Лапласа производной образа [4, стр. 224].
Пусть  — образ сигнала
— образ сигнала  . Тогда
. Тогда

(20)
где  — производная
— производная  -го порядка образа
-го порядка образа  .
.
Свойство интегрирования оригинала и образа
Пусть сигнал  есть результат интегрирования сигнала
есть результат интегрирования сигнала  :
:

(21)
Рассмотрим преобразование Лапласа  от
от  :
:

(22)
Изменим порядок интегрирования и получим:

(23)
Получили еще одно важнейшее свойство: образ интеграла от входного сигнала  равен образу
равен образу  этого сигнала, деленного на переменную
этого сигнала, деленного на переменную  . Это свойство также позволяет заменить интегральные уравнения и системы на алгебраические.
. Это свойство также позволяет заменить интегральные уравнения и системы на алгебраические.
Преобразование Лапласа свертки двух сигналов
Пусть сигнал  представляет собой свертку двух сигналов
представляет собой свертку двух сигналов  и
и  , определяемую соотношением:
, определяемую соотношением:

(24)
Важность интеграла свертки (24) в том, что им описывается результат прохождения сигнала  через линейный фильтр с импульсной характеристикой
через линейный фильтр с импульсной характеристикой  .
.
Обратим внимание, что пределы интегрирования от 0 до  обусловлены тем, что
обусловлены тем, что  и
и  отличны от нуля только для положительных значений переменной
отличны от нуля только для положительных значений переменной  .
.
Рассмотрим преобразование Лапласа  сигнала
сигнала  :
:

(25)
Поменяем местами операции интегрирования, и учтем свойство временного сдвига (14):

(26)
Таким образом, интеграл свертки заменяется произведением образов  входного сигнала
входного сигнала  и образа
и образа  импульсной характеристики фильтра
импульсной характеристики фильтра  .
.
Данное свойство также является очень важным, поскольку анализ многокаскадных фильтров заменяется простым произведением образов импульсных характеристик этих фильтров.
Выводы
В данном разделе мы рассмотрели преобразование Лапласа и его некоторые свойства.
Аппарат операционного исчисления является основным инструментом анализа
электрических цепей переменного тока, ввиду возможности замены операций
дифференцирования и интегрирования алгебраическим умножением и делением
на переменную  .
.
Подробнее использование преобразования Лапласа для анализа цепей
переменного тока будет рассмотрено в следующем разделе.
Список литературы
[1]
Будак, Б.М., Фомин, С.В.
Кратные интегралы и ряды.
Москва, Наука, 1965, 608 c.
[2]
Дёч, Г.
Руководство по практическому применению преобразования Лапласа.
Москва, Наука, 1965, 288 c.
[3]
Ильин, В.А., Позняк Э.Г.
Основы математического анализа.
Москва, Наука, 1965, 572 c.
[4]
Свешников, А.Г., Тихонов, А.Н.
Теория функций комплексной переменной.
Москва, Наука, 1967, 304 с.
Последнее изменение страницы: 24.06.2020 (20:13:06)
Непрерывное преобразование Лапласа
Одним из способов решения дифференциальных уравнений (систем уравнений) с постоянными коэффициентами является метод интегральных преобразований, который позволяет функцию вещественной переменной (оригинал функции) заменить функцией комплексной переменной (изображение функции). В результате операции дифференцирования и интегрирования в пространстве функций-оригиналов преобразуются в алгебраическое умножение и деление в пространстве функций-изображений. Одним из представителей метода интегральных преобразований является Преобразование Лапласа.
Непрерывное преобразование Лапласа – интегральное преобразование, связывающее функцию комплексной переменной ![]() (изображение функции) с функцией вещественной переменной
(изображение функции) с функцией вещественной переменной ![]() (оригинал функции). При этом функция вещественной переменной
(оригинал функции). При этом функция вещественной переменной ![]() должна удовлетворять следующим условиям:
должна удовлетворять следующим условиям:
— функция определена и дифференцируема на всей положительной полуоси вещественной переменной ![]() (функция удовлетворяет условиям Дирихле);
(функция удовлетворяет условиям Дирихле);
— значение функции до начального момента приравнивают к нулю ![]() ;
;
— возрастание функции ограничена экспоненциальной функцией, т.е. для функции вещественной переменной существуют такие положительные числа М и с, что ![]() при
при ![]() , где c – абсцисса абсолютной сходимости (некоторое положительное число).
, где c – абсцисса абсолютной сходимости (некоторое положительное число).
Преобразованием Лапласа (прямое интегральное преобразование) от функции вещественной переменной называется функция следующего вида (функция от комплексной переменной):

Функцию ![]() называют оригиналом функции, а функцию
называют оригиналом функции, а функцию ![]() называют ее изображением. Комплексная переменная
называют ее изображением. Комплексная переменная ![]() называется оператором Лапласа, где
называется оператором Лапласа, где ![]() — угловая частота,
— угловая частота, ![]() — некоторое положительное постоянное число.
— некоторое положительное постоянное число.
В качестве первого примера определим изображение для постоянной функции ![]()

В качестве второго примера определим изображение для косинусоидальной функции ![]() . С учетом формулы Эйлера косинусоидальную функцию можно представить в виде суммы двух экспонент
. С учетом формулы Эйлера косинусоидальную функцию можно представить в виде суммы двух экспонент  .
.

На практике для выполнения прямого преобразования Лапласа используются таблицы преобразований, в которых представлены оригиналы и изображения типовых функций. Ниже представлены некоторые из данных функций.
Оригинал и изображение для экспоненциальной функции

Оригинал и изображение для косинусоидальной функции

Оригинал и изображение для синусоидальной функции

Оригинал и изображение для экспоненциально затухающего косинуса

Оригинал и изображение для экспоненциально затухающего синуса

Следует отметить, что функция ![]() является функцией Хевисайда, которая принимает значение ноль при отрицательных значениях аргумента и принимает значение равное единице для положительных значений аргумента.
является функцией Хевисайда, которая принимает значение ноль при отрицательных значениях аргумента и принимает значение равное единице для положительных значений аргумента.
Свойства Преобразования Лапласа
• Теорема линейности
Преобразование Лапласа обладает свойством линейности, т.е. любое линейное соотношение между оригиналами функции справедливо для изображений этих функций.
![]()
Свойство линейности упрощает нахождение оригиналов сложных изображений, так как позволяет изображение функции представить в виде суммы простых слагаемых, а затем найти оригиналы каждого представленного слагаемого.
• Теорема о дифференцировании оригинала функции
Дифференцирование оригинала функции соответствует умножению изображения функции на оператор Лапласа.
— при ненулевых начальных условиях:


— при нулевых начальных условиях (частный случай):

Таким образом, операция дифференцирования функции заменяется арифметической операцией в пространстве изображений функции.
• Теорема об интегрировании оригинала функции
Интегрирование оригинала функции соответствует делению изображения функции на оператор Лапласа.

Таким образом, операция интегрирования функции заменяется арифметической операцией в пространстве изображений функции.
• Теорема подобия
Изменение аргумента функции (сжатие или расширение сигнала) во временной области приводит к обратному изменению аргумента и ординаты изображения функции.

Увеличение длительности импульса вызывает сжатие его спектральной функции и уменьшение амплитуд гармонических составляющих спектра.
• Теорема запаздывания
Запаздывание (сдвиг, смещение) сигнала по аргументу оригинала функции на интервал ![]() приводит к изменению фазочастотной функции спектра (фазового угла всех гармоник) на заданную величину без изменения модуля (амплитудной функции) спектра.
приводит к изменению фазочастотной функции спектра (фазового угла всех гармоник) на заданную величину без изменения модуля (амплитудной функции) спектра.
![]()
Полученное выражение справедливо для любого ![]()
• Теорема смещения
Запаздывание (сдвиг, смещение) сигнала по аргументу изображения функции приводит к умножению оригинала функции на экспоненциальный множитель
![]()
Теорема смещения с практической точки зрения применяется при определении изображений экспоненциальных функций.
• Теорема о свертке
Свертка является математической операцией, применённая к двум функциям ![]() и
и ![]() , порождающая третью функцию. Другими словами, имея реакцию некой линейной системы на импульс, можно с помощью свёртки вычислить реакцию системы на весь сигнал.
, порождающая третью функцию. Другими словами, имея реакцию некой линейной системы на импульс, можно с помощью свёртки вычислить реакцию системы на весь сигнал.

Таким образом, свертка оригиналов двух функций может быть представлена в виде произведения изображений этих функций. Теорему сверки используют при рассмотрении передаточных функций, когда определяется реакция системы (выходной сигнал от четырехполюсника) при подаче сигнал ![]() на вход четырехполюсника с импульсной переходной характеристикой
на вход четырехполюсника с импульсной переходной характеристикой ![]() .
.

Рис.1. Линейный четырехполюсник
Обратное преобразование Лапласа
Преобразование Лапласа является обратимым, т.е. функция вещественной переменной ![]() однозначно определяется из функции комплексной переменной
однозначно определяется из функции комплексной переменной ![]() . Для этого используется формула обратного преобразования Лапласа (формула Меллина, интеграл Бромвича), которая имеет следующий вид:
. Для этого используется формула обратного преобразования Лапласа (формула Меллина, интеграл Бромвича), которая имеет следующий вид:

В данной формуле пределы интегрирования означают, что интегрирование идет по бесконечной прямой, которая параллельна мнимой оси и пересекает вещественную ось в точке ![]() . С учетом того, что
. С учетом того, что ![]() последние выражение может быть переписано в следующем виде:
последние выражение может быть переписано в следующем виде:

На практике для выполнения обратного преобразования Лапласа изображение функции раскладывают на сумму простейших дробей методом неопределённых коэффициентов и для каждой дроби (в соответствии со свойством линейности) определяют оригинал функции, в том числе с учетом таблицы типовых функций. Данный способ справедлив для изображения функции, которая является правильной рациональной дробью. Следует отметить, что простейшая дробь может быть представлена в виде произведения линейных и квадратичных сомножителей с действительными коэффициентами в зависимости от типа корней знаменателя:
— в случае наличия нулевого корня в знаменателе, функция раскладывается на дробь типа: ![]()
— в случае наличия нулевого n -кратного корня в знаменателе, функция раскладывается на дробь типа: 
— в случае наличия действительного корня ![]() в знаменателе, функция раскладывается на дробь типа:
в знаменателе, функция раскладывается на дробь типа: 
— в случае наличия действительного n -кратного корня ![]() в знаменателе, функция раскладывается на дробь типа:
в знаменателе, функция раскладывается на дробь типа: 
— в случае наличия мнимого корня ![]() в знаменателе, функция раскладывается на дробь типа:
в знаменателе, функция раскладывается на дробь типа: 
— в случае наличия комплексно-сопряжённых корней ![]() в знаменателе, функция раскладывается на дробь типа:
в знаменателе, функция раскладывается на дробь типа: 
∙ В общем случае если изображение функции представляет собой правильную рациональную дробь (степень числителя меньше степени знаменателя рациональной дроби), то ее можно разложить на сумму простейших дробей.

Далее для каждой простейшей дроби определяется оригинал функции в соответствии с типовыми таблицами.

∙ В частном случае если знаменатель изображения функции раскладывается только на простые корни уравнения, то изображение функции можно разложить на сумму простейших дробей следующим образом:

Неизвестные коэффициенты ![]() могут быть определены методом неопределённых коэффициентов или упрощенным способом по следующей формуле:
могут быть определены методом неопределённых коэффициентов или упрощенным способом по следующей формуле:

![]() — значение функции в точке
— значение функции в точке ![]() ;
;
![]() — значение производной функции в точке
— значение производной функции в точке ![]() .
.
Оригинал данной функции будет определяться следующим образом:

В качестве примера определим оригинал функции, при условии, что его изображение определяется следующим образом:

Раскладываем знаменатель на множители и перепишем изображение функции с учетом введение в уравнение неизвестных коэффициентов:

Неизвестные коэффициенты в выражении будут определяться по формуле следующим образом:


Таким образом, изображение функции имеет следующий вид:

В результате определяем оригинал функции:
![]()
Следует отметить, что в случае если знаменатель имеет нулевой корень, то упрощенная формула для определения неопределённых коэффициентов имеет другой вид:

В качестве примера определим оригинал функции, при условии, что его изображение определяется следующим образом:

Раскладываем знаменатель на множители и перепишем изображение функции с учетом введение в уравнение неизвестных коэффициентов:

Неизвестные коэффициенты в выражении будут определяться по формуле следующим образом:



Таким образом, изображение функции имеет следующий вид:

В результате оригинал функции будет определяться следующим выражением:

Преобразования Лапласа применяются в математике, физике, оптике, электротехнике, технике автоматического управления, обработке сигналов и теории вероятности. Данное преобразование было предложено Пьером-Симоном де Лапласом в XVIII веке в процессе работы над теорией вероятности. В настоящее время преобразование Лапласа используется при решении систем дифференциальных и интегральных уравнений, а также при расчете/анализе передаточных функций линейных динамических систем, таких как электрические схемы, гармонические осцилляторы, оптические приборы и механические системы.
Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.
Операторный метод берет начало со времени анализа бесконечно малых величин, когда были обнаружены определенные аналогии между дифференциально-интегральными и алгебраическими уравнениями. В XIX в. был опубликован ряд работ по операционному исчислению М.Е. Ващенко-Захарченко, О. Хэвисайда, Д. Карсона и др. Однако строгое обоснование операторный метод получил только в XX в. на базе общей теории функциональных преобразований.
В основе операторного метода расчета переходных процессов лежит преобразование Лапласа, которое позволяет перенести решение из области функций действительного переменного t в область комплексного переменного р:
При этом операции дифференцирования и интегрирования функций времени заменяются соответствующими операциями умножения и деления функций комплексного переменного на оператор р, что существенно упрощает расчет, так как сводит систему дифференциальных уравнений к системе алгебраических. В операторном методе отпадает необходимость определения постоянных интегрирования. Этими обстоятельствами объясняется широкое применение этого метода на практике.
Различают прямое и обратное преобразование Лапласа. Прямое преобразование Лапласа определяется уравнением.
где f(t) — функция действительного переменного t, определенная при t 0 (при t < 0; f(t) = 0) и удовлетворяющая условиям ограниченного роста:
где множитель М и показатель роста с0 — положительные действительные числа. На рис. 7.1 изображена область определения функции комплексного переменного F(p).
Обратное преобразование Лапласа определяют из решения (7.2):
Функция F(p), определяемая уравнением (7.2), носит название изображения по Лапласу, а функция f(t) в (7.4) — оригинала. Следовательно, оригинал и изображение представляют собой пару функций действительного (t) и комплексного (p) переменного, связанных преобразованием Лапласа. Для сокращенной записи преобразований (7.2), (7.4) используют следующую символику
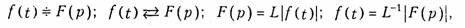
где L — оператор Лапласа. В дальнейшем для определенности будем использовать знак соответствия .
Рассмотрим основные свойства преобразований Лапласа.
Свойство линейности является следствием линейности преобразования Лапласа, его можно записать в форме
где ak — постоянные коэффициенты разложения. Свойство (7.5) легко доказать, если применить к левой части соотношения (7.5) прямое преобразование Лапласа (7.2).
Дифференцирование оригинала
При ненулевых начальных условиях: f(0–)¹ 0 дифференцирование оригинала соответствует следующему условию
Для доказательства (7.6) подставим f¢(t) в преобразование (7.2) в виде
Отсюда после интегрирования по частям получаем:
В случае нулевых начальных условий
Интегрирование оригинала
Доказательство осуществляется путем использования свойства дифференцирования оригинала (7.6), (7.7).
Изменение масштаба независимого переменного (теорема подобия)
где а — постоянный вещественный коэффициент. Свойство (7.9) легко доказывается путем замены независимой переменной t = atв прямом преобразовании Лапласа (7.2).
Смещение в области действительного переменного (теорема запаздывания)
Для доказательства (7.10) введем следующие обозначения:
Осуществим замену переменной t = t ± t0.
что и требовалось доказать.
Из соотношения (7.10) следует, что сдвиг оригинала по оси времени на t0 соответствует умножению изображения на .
Смещения в области комплексного переменного (теорема смещения)
Теорема (7.11) следует непосредственно из прямого преобразования Лапласа, если в (7.2) вместо f(t) подставить . Причем l может быть как действительной, так и комплексной величиной.
Дифференцирование и интегрирование оригинала по параметру (свойство коммутативности)
Для доказательства свойств (7.12), (7.13) достаточно продифференцировать или проинтегрировать прямое преобразование Лапласа (7.2) по параметру х.
Произведение изображений
Интегралы в (7.14) носят название свертки функций f1(t) и f2(t).
Дифференцирование изображения
Свойство (7.15) легко доказывается путем дифференцирования прямого преобразования Лапласа (7.2).
Интегрирование изображения
Данное свойство доказывается аналогично (7.15).
В заключение приведем предельные соотношения для оригинала и изображения:
Действительно, согласно свойства дифференцирования оригинала можно записать:
Учитывая, что , получаем:
Отсюда непосредственно следует соотношение (7.17). Аналогично доказывается равенство (7.18).
В качестве примера найдем изображение по Лапласу типовых сигналов. Для теоретических и экспериментальных исследований характеристик электрических цепей и передачи сообщений по каналам связи используются различные типы сигналов: гармонические колебания, уровни постоянных напряжений, последовательность прямоугольных импульсов и так далее. Особо важную роль в теоретических исследованиях электрических цепей играют испытательные сигналы в форме единичной функции 1(t) и единичной импульсной функции d(t) (функция Дирака).
Единичная функция
Единичная функция задается уравнением (рис. 7.2, а)
Изображение функции (7.19) будет равно:
Единичная импульсная функция (функция Дирака)
Эта функция называется еще d-функцией; она задается уравнением
Функция Дирака является физически нереализуемой математической абстракцией, однако обладает рядом интересных свойств и играет очень важную роль в теоретических исследованиях. Формально она может быть получена, например, предельным переходом (при t ® 0) единичного импульса (см. рис. 7.2, б), площадь которого равна единице:
Одним из интересных свойств функции d(t) является ее фильтрующее свойство, определяемое равенством (рис. 7.3):
Найдем изображение единичной импульсной функции в форме изображения разности двух единичных функций величины 1(t), сдвинутых друг относительно друга на t (рис. 7.4). Для этих функций с учетом теоремы запаздывания имеем:
Для результирующего изображения с учетом свойства линейности получим
Устремив t ® 0, найдем изображение единичной импульсной функции (d-функции):
Экспоненциальный сигнал при t > 0:
т. е.
Подобным же образом можно найти изображение по Лапласу других функций, удовлетворяющих условию (7.3). В литературе имеются специальные справочники, в которых приведены оригиналы и изображения широкого класса функций. В табл. 7.1 приведены оригиналы и их изображения наиболее часто встречающихся в теории электрических цепей функций.
