Какое свойство имеет медиана треугольника

У этого термина существуют и другие значения, см. Медиана.
Треугольник и его медианы.
Медиа́на треуго́льника (лат. mediāna — средняя) ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Иногда медианой называют также прямую, содержащую этот отрезок. Точка пересечения медианы со стороной треугольника называется основанием медианы.
Связанные определения[править | править код]
Три медианы, проходящие через общую точку
На рис. справа в треугольнике ABC через точку O проведены 3 медианы: AD, BE и CF. Тогда точка O пересечения 3 медиан разбивает каждую медиану на 2 отрезка прямых, один из них (который начинается в вершине, а заканчивается в точке пересечения O) мы назовем домедианой или предмедианой, а второй из них (который начинается в точке пересечения O, а заканчивается в точке его пересечения со стороной, противоположной вершине) мы назовем постмедианой.[1]
С помощью этих 2 понятий совсем просто формулируются некоторые теоремы геометрии. Например, в любом треугольнике отношение пред- и постмедианы равно двум.
Свойства[править | править код]
Основное свойство[править | править код]
Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Свойства медиан равнобедренного треугольника[править | править код]
В равнобедренном треугольнике две медианы, проведенные к равным сторонам треугольника, равны, а третья медиана одновременно является биссектрисой и высотой. Верно и обратное: если в треугольнике две медианы равны, то треугольник — равнобедренный, а третья медиана одновременно является биссектрисой и высотой угла при своей вершине.
У равностороннего треугольника все три медианы равны.
Свойства оснований медиан[править | править код]
- Теорема Эйлера для окружности девяти точек: основания трёх высот произвольного треугольника, середины трёх его сторон (основания его медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (так называемой окружности девяти точек).
- Отрезок, проведенный через основания двух любых медиан треугольника, является его средней линией. Средняя линия треугольника всегда параллельна той стороне треугольника, с которой она не имеет общих точек.
- Следствие (теорема Фалеса о параллельных отрезках). Средняя линия треугольника равна половине длины той стороны треугольника, которой она параллельна.
- Теркем доказал теорему Теркема.[2] Она утверждает, что если окружность девяти точек пересекает стороны треугольника или их продолжения в 3 парах точек (в 3 основаниях соответственно высот и медиан), являющихся основаниями 3 пар чевиан, то, если 3 чевианы для 3 из этих оснований пересекаются в 1 точке (например 3 медианы пересекаются в 1 точке), то 3 чевианы для 3 других оснований также пересекаются в 1 точке (т. е. 3 высоты также обязаны пересечься в 1 точке).
Другие свойства[править | править код]
- Если треугольник разносторонний (неравносторонний), то его биссектриса, проведённая из любой вершины, лежит между медианой и высотой, проведёнными из той же вершины.
- Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
- Треугольник делится тремя медианами на шесть равновеликих треугольников. Центры описанных окружностей этих шести треугольников лежат на одной окружности, которая называется окружностью Ламуна.
- Из отрезков, образующих медианы, можно составить треугольник, площадь которого будет равна 3/4 от всего треугольника. Длины медиан удовлетворяют неравенству треугольника.
- В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
- Большей стороне треугольника соответствует меньшая медиана.
- Отрезок прямой, симметричный или изогонально сопряжённый внутренней медиане относительно внутренней биссектрисы, называется симедианой треугольника. Три симедианы проходят через одну точку — точку Лемуана.
- Медиана угла треугольника изотомически сопряжена самой себе.
Бесконечно удаленная прямая — трилинейная поляра центроида
- Трилинейная поляра центроида (точки пересечения трех медиан) — бесконечно удаленная прямая (см. рис.).
Основные соотношения[править | править код]
Чтобы вычислить длину медианы, когда известны длины сторон треугольника, применяется теорема Аполлония (выводится через теорему Стюарта или достроением до параллелограмма и использованием равенства в параллелограмме суммы квадратов сторон и суммы квадратов диагоналей):
где — медианы к сторонам треугольника соответственно.
В частности, сумма квадратов медиан произвольного треугольника составляет 3/4 от суммы квадратов его сторон:
.
Обратно, можно выразить длину произвольной стороны треугольника через медианы:
где — медианы к соответствующим сторонам треугольника, — стороны треугольника.
Площадь любого треугольника, выраженная через длины его медиан:
где — полусумма длин медиан.
См. также[править | править код]
- Биссектриса
- Высота треугольника
- Инцентр
- Симедиана
- Центроид
- Чевиана
Примечания[править | править код]
Литература[править | править код]
- Ефремов Дм. Новая геометрия треугольника, 1902 год.
Медиана треугольника, так же, как и высота служит графическим параметром, определяющим весь треугольник, значение его сторон и углов. Три значения: медианы, высоты и биссектрисы – это, как штрих-код на товаре, наша задача просто уметь его считать.

Определение
Медиана – это отрезок, соединяющий высоту и середину противоположной стороны. В треугольнике три вершины, а значит и медианы три. Медианы не всегда совпадают с высотами или биссектрисами. Чаще всего это отдельные отрезки.
Свойства медиан
- Медиана равнобедренного треугольника, проведенная к основанию, совпадает с высотой и биссектрисой. В равностороннем треугольнике все медианы совпадают с биссектрисами и высотами.
- Все медианы треугольника пересекаются в одной точке.
- Медиана делит треугольник на два равновеликих, а три медианы, на 6 равновеликих треугольника.
Равновеликими называют треугольники, площади которых равны.

Рис. 1. Три медианы образуют 6 равновеликих треугольника.
- Точка пересечения медиан делит их в отношении 2:1, считая от вершины.
- Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы.
Задачи
Все эти свойства несложно запомнить, они легко закрепляются на практике. Для большего понимания темы, решим несколько задач:
- В прямоугольном треугольнике известны катеты, которые равны a=3 и b=4. Найти значение медианы m, проведенной к гипотенузе c.
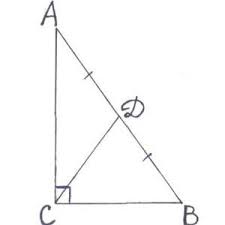
Рис. 2. Рисунок к задаче.
Для того, чтобы найти значение медианы, нам необходимо найти гипотенузу, так как медиана, проведенная к гипотенузе равна ее половине. Гипотенуза через теорему Пифагора: $$a^2+b^2=c^2$$
$$c=sqrt{a^2+b^2}=sqrt{9+16}=sqrt{25}=5$$
Найдем значение медианы: $$m={cover2}={5over2}=2,5$$ – получившееся число и есть значение медианы.
Значения медиан в треугольнике не равны. Поэтому нужно обязательно представлять, какую именно величину необходимо найти.
- В треугольнике известны значения сторон : a=7; b=8; c=9. Найти значение медианы, опущенной к стороне b.

Рис. 3. Рисунок к задаче.
Чтобы решить эту задачу нужно воспользоваться одной из трех формул для нахождения медианы по сторонам треугольника:
$$m^2 ={1over2}*(a^2+c^2-b^2)$$
Как видно, главное здесь запомнить коэффициент при скобках и знаки у значения сторон. Знаки запомнить проще всего – вычитается всегда сторона, к которой опущена медиана. В нашем случае это b, но может быть любая другая.
Подставим значения в формулу и найдем величину медианы: $$m=sqrt{{1over2}*(a^2+c^2-b^2)}$$
$$m=sqrt{{1over2}*(49+81-64)}=sqrt{33}$$ – оставим результат в виде корня.
- В равнобедренном треугольнике медиана, проведенная к основанию равна 8, а само основание 6. Вместе с оставшимися двумя, эта медиана делит треугольник на 6 треугольников. Найти площадь каждого из них.
Медианы, разбивают треугольник на шесть равновеликих. Значит, площади малых треугольников будут равны между собой. Достаточно найти площадь большего и поделить ее на 6.
Дана медиана, проведенная к основанию, в равнобедренном треугольнике она является биссектрисой и высотой. Значит в треугольнике известны основание и высота. Можно найти площадь.
$$S={1over2}*6*8=24$$
Площадь каждого из малых треугольников: $${24over6}=4$$
Что мы узнали?
Мы узнали, что такое медиана. Определили свойства медианы, и нашли решение типовых задач. Поговорили о базовых ошибках и разобрались как просто и быстро запомнить формулу нахождения медианы через стороны треугольника.
Тест по теме
Оценка статьи
Средняя оценка: 4.7. Всего получено оценок: 129.
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
1. Что такое медиана?
Это очень просто!
Возьми треугольник:

Отметь на какой-нибудь его стороне середину .

И соедини с противоположной вершиной!

Получившаяся линия и есть медиана.
Медиана – линия, проведённая из вершины треугольника к середине противоположной стороны.
2. Свойства медианы.
Какие же хорошие свойства есть у медианы?
1) Вот представим, что треугольник – прямоугольный. Бывают же такие, верно?
 | Тогда медиана равна половине гипотенузы! |
Почему??? При чём тут прямой угол?
Давай смотреть внимательно. Только не на треугольник, а на … прямоугольник. Зачем, спросишь?
А вот ты ходишь по Земле – ты видишь, что она круглая? Нет, конечно, для этого на Землю нужно смотреть из космоса. Вот и мы посмотрим на наш прямоугольный треугольник «из космоса».
Итак, рассмотрим прямоугольник .

Ты заметил, что наш треугольник – ровно половина этого прямоугольника?
Проведём диагональ :

Помнишь ли ты, что диагонали прямоугольника равны и делятся точкой пересечения пополам? (Если не помнишь, загляни в тему «Параллелограмм, прямоугольник, ромб…»)
Но одна из диагоналей – – наша гипотенуза! Значит, точка пересечения диагоналей – середина гипотенузы . Она называлась у нас .

Значит, половина второй диагонали – наша медиана . Диагонали равны, их половинки, конечно же, тоже. Вот и получим
Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы.
Более того, так бывает только в прямоугольном треугольнике!
Если медиана равна половине стороны, то треугольник прямоугольный, и эта медиана проведена к гипотенузе.
Доказывать это утверждение мы не будем, а чтобы в него поверить, подумай сам: разве бывает какой-нибудь другой параллелограмм с равными диагоналями, кроме прямоугольника? Нет, конечно! Ну вот, значит, и медиана может равняться половине стороны только в прямоугольном треугольнике.
Давай посмотрим, как это свойство помогает решать задачи.
Вот, задача:
В стороны ; . Из вершины проведена медиана . Найти , если .
Рисуем:
 | Сразу вспоминаем, это если , то ! |
Ура! Можно применить теорему Пифагора! Видишь, как здорово? Если бы мы не знали, что медиана равна половине стороны только в прямоугольном треугольнике, мы никак не могли бы решить эту задачу. А теперь можем!
Применяем теорему Пифагора:
 | Вот и ответ! |
2) А теперь пусть у нас будет не одна, а целых три медианы! Как же они себя ведут?
Запомни очень важный факт:
Сложно? Смотри на рисунок:
 | Медианы , и пересекаются в одной точке. |
И….( доказываем это в следующем уровне теории, а пока запомни!):
- – вдвое больше, чем ;
- – вдвое больше, чем ;
- – вдвое больше, чем .
Не устал ещё? На следующий пример сил хватит? Сейчас мы применим всё, о чём говорили!
Задача: В треугольнике проведены медианы и , которые пересекаются в точке . Найти , если
 | Решение — треугольник прямоугольный! Значит, . (Применили то, что медиана, проведённая к гипотенузе равна половине гипотенузы). |
Найдём по теореме Пифагора:
Значит, .
А теперь применим знания про точку пересечения медиан.
Давай обозначим . Отрезок , а . Если не все понятно – посмотри на рисунок.
Мы уже нашли, что .
Значит, ; .
В задаче нас спрашивают об отрезке .
В наших обозначениях .
Значит, .
Ответ: .
Понравилось? Старайся теперь сам применять знания про медиану!
МЕДИАНА. СРЕДНИЙ УРОВЕНЬ
1. Медиана делит сторону пополам.
Медиана — линия, проведенная из вершины треугольника к середине противоположной стороны.
 | Посмотри на рисунок. Линия – медиана. |
Итак,
Медиана делит сторону пополам.
И все? А может, она ещё что-нибудь делит пополам? Представь себе, что это так!
2. Теорема: медиана делит площадь пополам.
Почему? А давай вспомним самую простую форму площади треугольника.
 |
И применим эту формулу аж два раза!

Посмотри, медиана разделила на два треугольника: и . Но! Высота-то у них одна и та же – ! Только в эта высота опускается на сторону , а в – на продолжение стороны . Удивительно, но вот бывает и так: треугольники разные, а высота – одна. И вот, теперь-то и применим два раза формулу .
1) B :
| » » – это » » – это |
2) B :
| » » – это » » – это опять |
Запишем ещё раз:
;
Но ! (Посмотри на рисунок или вспомни, что – медиана).
Значит, — площадь разделилась на две равные части. Ура! Доказали теорему. И получилось совсем несложно — всего-то одна формула площади.
3. Три медианы треугольника

Что бы это такое значило? Посмотри на рисунок. На самом деле утверждений в этой теореме целых два. Ты это заметил?
Первое утверждение: медианы пересекаются в одной точке.
Второе утверждение: точкой пересечения медианы делятся в отношении , считая от вершины.
Давай попробуем разгадать секрет этой теоремы:
 | Сначала проведем не все три, а только две медианы. Они-то уж точно пересекутся, правда? Обозначим точку их пресечения буквой . |
Соединим точки и . Что получилось?
 | Конечно, — средняя линяя . Ты помнишь, что это значит?
|
А теперь проведем ещё одну среднюю линию: отметим середину – поставим точку , отметим середину — поставим точку .
Теперь – средняя линия . То есть
- параллельна ;
- .
Заметил совпадения? И , и – параллельны . И , и .
Что из этого следует?
- параллельна ;
 | Посмотри теперь на четырехугольник . У какого четырехугольника противоположные стороны ( и ) параллельны и равны? |
Конечно же, только у параллелограмма!
Значит, – параллелограмм. Ну и что? А давай вспомним свойства параллелограмма. Например, что тебе известно про диагонали параллелограмма? Правильно, они делятся точкой пересечения пополам.
Снова смотрим на рисунок.
 | Получилось, что
|
То есть — медиана разделена точками и на три равные части. И точно так же .
Значит, точкой обе медианы разделились именно в отношении , то есть и .
Что же будет происходить с третьей медианой? Давай вернемся в начало. О, ужас?! Нет, сейчас будет все гораздо короче. Давай выбросим медиану и проведем медианы и .

А теперь представим, что мы провели точно такие же рассуждения, как для медиан и . Что тогда?
Получится, что медиана разделит медиану абсолютно точно так же: в отношении , считая от точки .
Но сколько же может быть точек на отрезке , которые делят его в отношении , считая от точки ?
Конечно же, только одна! И мы её уже видели – это точка .
Что же получилось в итоге?
Медиана точно прошла через ! Все три медианы через неё прошли. И все разделились в отношении , считая от вершины.
Вот и разгадали (доказали) теорему. Разгадкой оказался параллелограмм, сидящий внутри треугольника.
4. Формула длины медианы
Как же найти длину медианы, если известны стороны? А ты уверен, что тебе это нужно? Откроем страшную тайну: эта формула не очень полезная. Но всё-таки мы её напишем, а доказывать не будем (если интересно доказательство – смотри следующий уровень).
 | Итак, |
5. Медиана в прямоугольном треугольнике.
Теорема:
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.

Как бы понять, отчего так выходит?
Давай смотреть внимательно. Только не на треугольник, а на прямоугольник.
Итак, рассмотрим прямоугольник .

Ты заметил, что наш треугольник – ровно половина этого прямоугольника?
Проведём диагональ

Помнишь ли ты, что диагонали прямоугольника равны и делятся точкой пересечения пополам? (Если не помнишь, загляни в тему «Параллелограмм, прямоугольник, …»)
Но одна из диагоналей – – наша гипотенуза! Значит, точка пересечения диагоналей – середина гипотенузы . Она называлась у нас .

Значит, половина второй диагонали – наша медиана . Диагонали равны, их половинки, конечно же, тоже. Вот и получим
Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы.
Более того, так бывает только в прямоугольном треугольнике!
Если медиана равна половине стороны, то треугольник прямоугольный, и эта медиана проведена к гипотенузе.
Доказывать это утверждение мы не будем, а чтобы в него поверить подумай сам: разве бывает какой – нибудь другой параллелограмм с равными диагоналями, кроме прямоугольника? Нет, конечно! Ну вот, значит, и медиана может равняться половине стороны только в прямоугольном треугольнике. Давай посмотрим, как это свойство помогает решать задачи.
Вот, задача:
В стороны ; . Из вершины проведена медиана . Найти , если .
Рисуем:
 | Сразу вспоминаем, это если , то ! |
Ура! Можно применить теорему Пифагора! Видишь, как здорово? Если бы мы не знали, что медиана равна половине стороны только в прямоугольном треугольнике, мы никак не могли бы решить эту задачу. А теперь можем!
Применяем теорему Пифагора:
 | Вот и ответ! |
МЕДИАНА. КОРОТКО О ГЛАВНОМ
1. Медиана делит сторону пополам.
 | Медиана — линия, проведенная из вершины треугольника к середине противоположной стороны. |
2. Теорема: медиана делит площадь пополам
 | Но , значит, |
3. Три медианы треугольника
 | Три медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении , считая от вершины. |
4. Формула длины медианы
 |
5. Медиана в прямоугольном треугольнике
 | В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы. |
Обратная теорема: если медиана равна половине стороны, то треугольник прямоугольный и эта медиана проведена к гипотенузе.
ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!
Стать учеником YouClever,
Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц»,
А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.
