Какое свойство имеет биссектриса

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 марта 2020;
проверки требуют 6 правок.
Биссектриса AD делит пополам угол A
Биссектри́са (от лат. bi- «двойное», и sectio «разрезание») угла — луч, исходящий из вершины угла и делящий этот угол на два равных угла. Можно также определить биссектрису как геометрическое место точек внутри угла, равноудалённых от сторон этого угла[1].
Биссектрисой треугольника называется отрезок биссектрисы угла, проведенный от вершины угла до её пересечения с противолежащей стороной. У треугольника существуют три биссектрисы, соответствующие трём его вершинам.
Связанные определения[править | править код]
- Точка пересечения биссектрисы угла треугольника с его стороной, не являющейся стороной этого угла, называется основанием биссектрисы.
Свойства[править | править код]
Свойства точек пересечения биссектрис[править | править код]
- Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности (инцентре).
- Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трёх вневписанных окружностей этого треугольника.
- Каждая биссектриса треугольника делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины.
- Гипербола Фейербаха — описанная гипербола, проходящая через ортоцентр и центр вписанной окружности (он же — инцентр или точка пресечения внутренних биссектрис треугольника). Её центр лежит в точке Фейербаха. Подерные и чевианные окружности точек на гиперболе Фейербаха проходят через точку Фейербаха.
Свойства, связанные с углами[править | править код]
- Каждая внутренняя (внешняя) биссектриса угла треугольника, выходящая из его вершины, делит этот внутренний (внешний) угол треугольника пополам (на две равные половинки).
- Угол между биссектрисами двух смежных углов (между внутренними и внешними биссектрисами углов треугольника при одной вершине) равен 90 градусам.
- Внутренняя биссектриса угла треугольника изогонально сопряжена самой себе.
Свойства, связанные с дугами[править | править код]
- Свойство биссектрисы вписанного угла: биссектриса вписанного угла делит на две равные части дугу, на которую этот угол опирается.
- То же свойство верно и для биссектрисы центрального угла.
Свойства биссектрис равнобедренного треугольника[править | править код]
- Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса), и третья биссектриса одновременно является медианой и высотой того угла, из которого она выходит.
- Верно и обратное: в равнобедренном треугольнике две биссектрисы равны, и третья биссектриса одновременно является медианой и высотой.
- В равнобедренном треугольнике внутренняя биссектриса угла, противоположного основанию треугольника, является медианой и высотой.
- Одна и только одна биссектриса внешнего угла неравностороннего треугольника может быть параллельна противоположной стороне — основанию, если треугольник равнобедренный.
- У равностороннего треугольника все три биссектрисы внешних углов параллельны противоположным сторонам.
- У равностороннего треугольника все три внутренние биссектрисы равны.
Свойства оснований биссектрис[править | править код]
- Теорема о биссектрисе (см. рис.): Биссектриса внутреннего угла треугольника делит противоположную сторону (то есть делит своим основанием противоположную сторону) в отношении, равном отношению двух прилежащих сторон. То есть или .
- Теорема о биссектрисе — частный случай теоремы Штейнера.
- Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника (Одна и только одна биссектриса внешнего угла треугольника может быть параллельна противоположной стороне — основанию, если треугольник равнобедренный. У равностороннего треугольника все три биссектрисы внешних углов параллельны противоположным сторонам. Других возможностей нет).
- Биссектриса внутреннего угла треугольника делит противоположную сторону изотомически по отношению к антибиссектрисе того же угла.
- Окружности, построенные, как на диаметре, на отрезке, соединяющем основания внутренней и внешней биссектрисы, выпущенных из одного угла, проходят через точки Аполлония.
- Через точку Фейербаха проходит окружность, проведённая через основания биссектрис .[4]
Свойства осей биссектрис[править | править код]
- Если биссектрисы внешних углов треугольника не параллельны противоположным сторонам, то их основания лежат на одной прямой, называемой осью внешних биссектрис.
- Точка Лемуана треугольника лежит на прямой Обера четырёхсторонника, образованного четырьмя осями биссектрис.
Другие свойства[править | править код]
- Если треугольник разносторонний (неравносторонний), то внутренняя биссектриса, проведённая из любой его вершины, лежит между внутренними медианой и высотой, проведёнными из той же вершины.
- Расстояния от сторон угла до любой точки биссектрисы одинаковы.
- Построение треугольника по трем заданным биссектрисам с помощью циркуля и линейки невозможно,[5] причём даже при наличии трисектора.[6]
- Три внешние биссектрисы любого треугольника пересекаются в трёх разных точках, которые являются центрами вневписанных окружностей исходного треугольника или вершинами так называемого треугольника трёх внешних биссектрис исходного треугольника[7].
Длина биссектрис в треугольнике[править | править код]
Для выведения нижеприведённых формул можно воспользоваться теоремой Стюарта.
, где — полупериметр.
Для трёх биссектрис углов , и с длинами соответственно и , справедлива формула[8]
,
,
где:
- — стороны треугольника против вершин соответственно,
- — внутренние углы треугольника при вершинах соответственно,
- — высота треугольника, опущенная на сторону .
- — длина внутренней биссектрисы, проведённой к стороне ,
- — длины отрезков, на которые внутренняя биссектриса делит сторону ,
- — длина внешней биссектрисы, проведённой из вершины к продолжению стороны .
- — длины отрезков, на которые внешняя биссектриса делит сторону и её продолжение до основания самой биссектрисы.
- Если медиана , высота и внутренняя биссектриса выходят из одной и той же вершины треугольника, около которого описана окружность радиуса , тогда[9]:p.122,#96
Длина частей биссектрис в треугольнике[править | править код]
Уравнения биссектрис[править | править код]
Мнемоническое правило (шуточное)[править | править код]
- Биссектриса — это крыса, которая бегает по углам и делит угол пополам.
См. также[править | править код]
- Антибиссектриса
- Высота (геометрия)
- Высота треугольника
- Инцентр
- Медиана треугольника
- Симедиана
- Теорема о биссектрисе
- Ось внешних биссектрис или антиортовая ось
- Треугольник
- Треугольник трёх внешних биссектрис
- Центроид
- Чевиана
Примечания[править | править код]
- ↑ Иванов А. Б. Биссектриса угла // Математическая энциклопедия / И. М. Виноградов (гл. ред.). — М.: Советская энциклопедия, 1977. — Т. 1. — С. 496. — 576 с. — 150 000 экз.
- ↑ Kimberling, Clark (1994), Central Points and Central Lines in the Plane of a Triangle, Mathematics Magazine Т. 67 (3): 163–187, DOI 10.2307/2690608.
- ↑ v. Nagel, C. H. (1836), Untersuchungen über die wichtigsten zum Dreiecke gehörenden Kreise, Leipzig.
- ↑ Акопян А. В., Заславский А. А.. Геометрические свойства кривых второго порядка. — 2-е изд., дополн.. — 2011. — С. 105.
- ↑ Кто и когда доказал невозможность построения треугольника по трем биссектрисам?. Дистанционный консультационный пункт по математике МЦНМО.
- ↑ Можно ли построить треугольник по трем биссектрисам, если кроме циркуля и линейки разрешается использовать трисектор. Дистанционный консультационный пункт по математике МЦНМО.
- ↑ Стариков В. Н. Исследования по геометрии// Сборник публикаций научного журнала Globus по материалам V-й международной научно-практической конференции «Достижения и проблемы современной науки» г. Санкт-Петербург: сборник со статьями (уровень стандарта, академический уровень). С-П.: Научный журнал Globus, 2016. С. 99-100
- ↑ Simons, Stuart. Mathematical Gazette 93, March 2009, 115—116.
- ↑ Altshiller-Court, Nathan, College Geometry, Dover Publ., 2007.
Литература[править | править код]
- Коган Б. Ю. Приложение механики к геометрии. — М.: Наука, 1965. — 56 с.
- Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 30-31. — ISBN 5-94057-170-0.
Базовым понятием и одним из наиболее интересных и полезных объектов школьной математики является биссектриса. С её помощью доказываются многие положения планиметрии, упрощается решение задач.
Известные свойства позволяют рассматривать геометрические фигуры с разных точек зрения. Появляется вариативность при выборе пути доказательств.
Становится возможным использование инструмента алгебры, например, свойство пропорции, нахождение неизвестных величин, решение алгебраических уравнений при рассмотрении геометрических вопросов.
Что такое биссектриса в геометрии
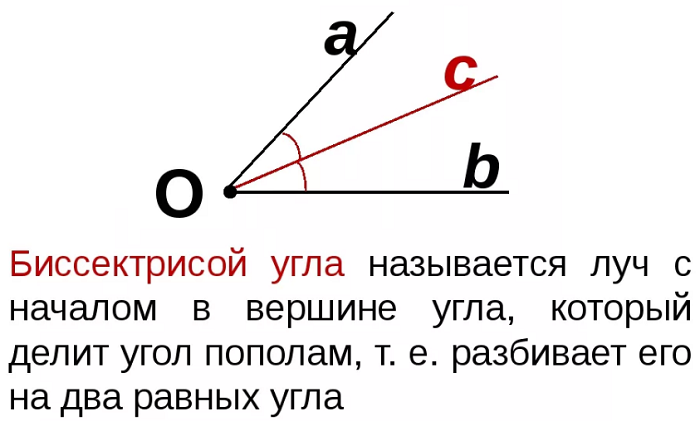
Рассматривают луч, выходящий из вершины угла или его часть (отрезок), который делит угол пополам. Такой луч (или, соответственно, отрезок) называется биссектрисой.
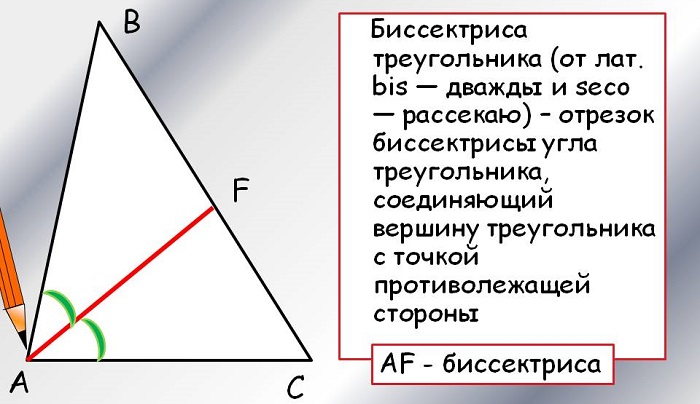
Часто для треугольников определение немного сужают, говоря об отрезке, соединяющем вершину угла, делящем его пополам, с точкой на противолежащей стороне. При этом рассматривается внутренняя область фигуры.
В то же время, часто при решении задач используются прямые, делящие внешние углы на два равных.
Биссектриса прямоугольного треугольника
Для прямоугольного треугольника одна из биссектрис образует равные углы, величины которых хорошо просчитываются (45 градусов).
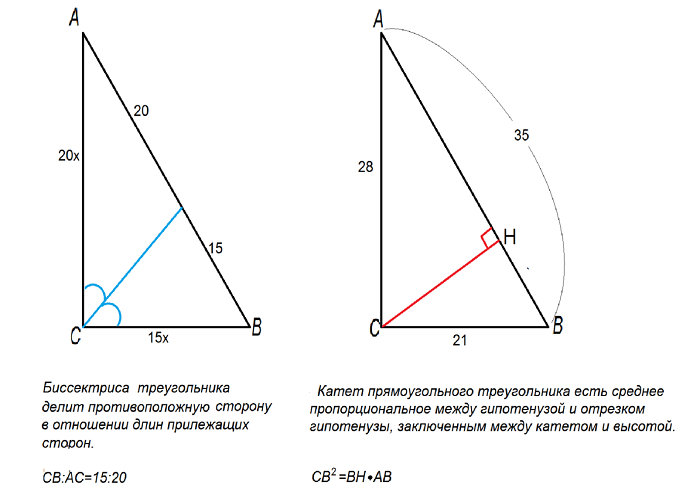
Это помогает вычислять углы при решении задач, связанных с фигурами, которые можно представить в виде прямоугольных треугольников или прямоугольников.
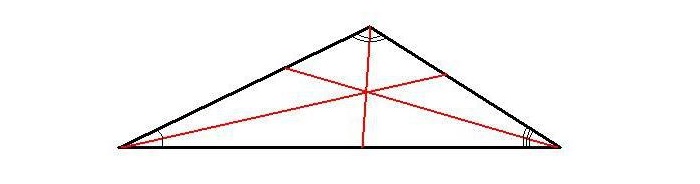
В тупоугольном треугольнике биссектриса делит больший угол на равные части, величина которых меньше 900.
Свойства биссектрисы треугольника
1. Каждая точка этой линии равноудалена от сторон угла. Часто эту характеристику выбирают в качестве определения, поскольку верно и обратное утверждение для любого произвольного треугольника. Это позволяет находить и радиус вписанной окружности.
2. Все внутренние отрезки, делящие углы пополам, пересекаются в одной точке, которая является центром окружности, вписанной в фигуру, т. е. точка пересечения находится на равных расстояниях от сторон.
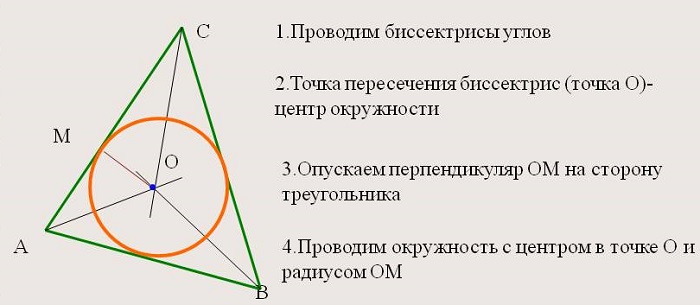
Данное свойство позволяет решать целый класс разнообразных задач, выводить формулы для радиусов вписанных окружностей правильных многоугольников.
Благодаря этому утверждению, легко доказывается следующее правило:
Площадь описанного многоугольника равна:
S = p∗r
где p – полупериметр, а r – радиус вписанной окружности.
Это позволяет находить решение не только планиметрических, но и стереометрических задач.
Важную роль играют внешние биссектрисы треугольника. Вместе с внутренними они образуют прямые углы;
3. Сумма величин двух прилежащих сторон, делённая на длину противолежащей стороны, задаёт отношение частей биссектрисы (считая от вершины), полученных точкой пересечения всех трёх соответствующих линий.
Некоторые виды геометрических фигур, в силу своих особенностей, порождают особые примечательные характеристики;
4. В равнобедренном треугольнике биссектриса, проведённая к основанию, одновременно является медианой и высотой. Две другие – равны между собой.
В этом случае основание параллельно внешней биссектрисе.
Обратное положение также имеет место. Если прямая проведена параллельно основанию равнобедренного треугольника через некоторую вершину, то внешняя биссектриса при этой вершине является частью этой линии;
5. Для равностороннего многоугольника важной характеристикой считается равенство всех биссектрис;
6. У правильного треугольника все внешние биссектрисы параллельны сторонам;
7. Выделяют несколько особенностей, среди которых есть следующая теорема:
«Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам».
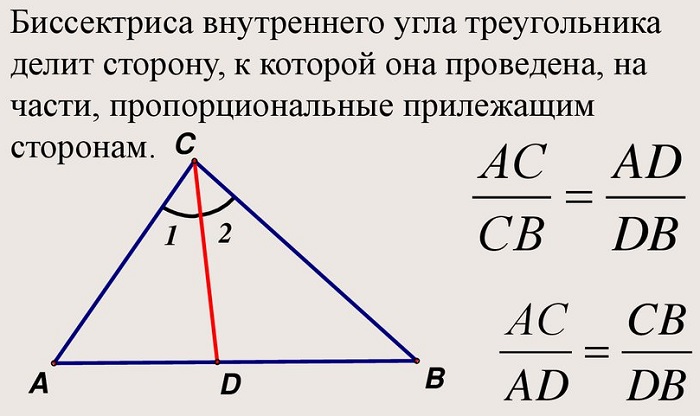
Обратное утверждение («Прямая делит сторону на отрезки, пропорциональные двум другим сторонам») выражает признаки того, что рассматриваемая линия является внутренней биссектрисой;
8. Разносторонний треугольник позволяет определить взаимное расположение его высоты, медианы и биссектрисы, проведённых из одной точки. В частности, медиана и высота располагаются по разные стороны от третьей линии.
Все формулы биссектрисы в треугольнике
В зависимости от исходных данных, длина биссектрисы, проведённой к стороне C, lc, равна:

Примеры решения задач
Задача №1
В ΔABC ∠C = 90°, проведена биссектриса острого угла. Отрезок, соединяющий её основание с точкой пересечения медиан, перпендикулярен катету. Найти углы заданной фигуры.
Решение.
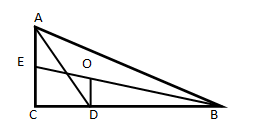
Пусть ∠ACB = 90°, AD – биссектриса, BE – медиана, O – точка пересечения медиан, OD⊥BC.
Тогда OE : OB = 1 : 2по свойству медиан.
Так как OD⊥BC, то ODIIOC, следовательно, ΔBOD ∼ ΔBEC по второму признаку подобия, поэтому, по свойству подобных фигур, CD : DB = 1 : 2.
Это означает, что CA : AB = 1 : 2.
Так как катет равен половине гипотенузы, то ∠ABC = 30°, откуда ∠CAB = 60°.
Ответ: 90°, 60°, 30°.
Задача №2
Диагональ параллелограмма делит его острый угол пополам. Доказать, что этот параллелограмм является ромбом.
Доказательство.
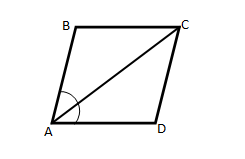
Так как ABCD – параллелограмм, то ∠DAC = ∠ACB, как накрест лежащие при параллельных прямых AD, BC и секущей AC.
По условию, ∠DAC = ∠ACB = ∠BAC, поэтому ΔACB равнобедренный, то есть AB = BC, следовательно, ABCD – ромб.
Доказано.
Биссектриса треугольника – это уникальный отрезок; он один из самых сложных по восприятию и пониманию. Легко понять и осознать, что такое высота, можно разобраться с определением и назначением медианы, но биссектрисы – это сложно. Просто потому, что основой для понимания биссектрисы служит понимание угла, а это не так легко усвоить, как величину отрезка.

Определения
Какие определения нам понадобятся в процессе работы? Во-первых, это определение биссектрисы.
Биссектриса – это луч, имеющий начало в вершине угла и делящий угол пополам.
Биссектриса треугольника – это отрезок биссектрисы, которой начинается в вершине треугольника и заканчивается на стороне, противолежащей этой вершине.
Вписанная окружность – это окружность, которая касается всех сторон треугольника. Треугольник в этом случае называется описанным.
Теперь обозначим основные свойства биссектрисы и приведем для них доказательства.
Первое, что нужно обозначить, это различие понятий биссектрисы и биссектрисы треугольника. Это похожие вещи, но свойства биссектрис углов треугольников не будут действовать на все биссектрисы. Это нужно запомнить.
Свойства биссектрисы треугольника
- Биссектриса в треугольнике делит сторону на отрезки, пропорциональные прилежащим сторонам.
Проведем в треугольнике АВС биссектрису ВК. После этого проведем прямую СМ, параллельную этой биссектрисе так, что точка М будет являться точкой пересечения продолжения стороны АВ.
Тогда два параллельных отрезка ВК и МС отсекут от сторон угла ВАС пропорциональные отрезки. То есть: АВ:АК=ВМ:КС. Докажем, что ВМ=ВС. Для этого посмотрим на треугольник ВМС. Угол АВК равен углу ВМС, как соответственные углы параллельных прямых при секущей АМ. С другой стороны угол КВС равен углу ВСМ, как накрест лежащие при параллельных прямых и секущей ВС. Но при этом угол АВК равен углу КВС, так как ВК – это биссектриса. Запишем все в виде равенств для большего понимания.
$$АВК = ВМС$$
$$КВС = ВСМ$$
$АВК = КВС$, значит углы ВМС и МСВ равны, а треугольник МВС – равнобедренный. Тогда $ВМ=ВС$ и $АВ:АК=ВС:СК$. Что и требовалось доказать.

Рис. 1. Первое свойство
- Биссектриса равноудалена от сторон угла, в котором она проведена.
Это свойство не биссектрисы треугольника, а любой биссектрисы, поэтому ее доказательство проще рассматривать на рисунке угла.
Нарисуем угол АВС и проведем в нем биссектрису ВМ. Расстояние от биссектрисы до стороны в любой точке это перпендикуляр. Поэтому выберем произвольную точку на биссектрисе. Назовем ее D и опустим перпендикуляр на сторону АВ в точку Р и на сторону ВС в точку N. Тогда мы получим два прямоугольных треугольника: DРВ и DNB, равные между собой по гипотенузе ВD, которая будет общей стороной треугольников, и острому углу, так как угол PBD равен углу DBN, так как ВМ – биссектриса. Значит, и стороны PD=DN – как соответственные элементы. Доказательство простое, но изящное. Знание этого свойство поможет в доказательстве следующей теоремы.

Рис. 2. Второе свойство
- Биссектрисы треугольника пересекаются в одной точке, и эта точка служит центром вписанной окружности. Это доказывается очень просто, необходимо из точки пересечения опустить перпендикуляры к каждой стороне.

Рис. 3. Третье свойство
Что мы узнали?
Мы узнали, что такое биссектриса треугольника и чем она отличается от обычной биссектрисы. Выделили три свойства биссектрисы треугольника, которые пригодятся при решении задач и доказательстве теорем.
Тест по теме
Оценка статьи
Средняя оценка: 3.9. Всего получено оценок: 182.
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Биссектриса треугольника и ее свойства
СОДЕРЖАНИЕ СТАТЬИ
Знаешь ли ты, что такое середина отрезка? Конечно же знаешь. А центр круга? Тоже.
А что такое середина угла?
Ты можешь сказать, что такого не бывает. Но почему же, отрезок можно разделить пополам, а угол нельзя? Вполне можно – только не точкой, а…. линией.
Помнишь шутку: биссектриса это крыса, которая бегает по углам и делит угол пополам.
Так вот, настоящее определение биссектрисы очень похоже на эту шутку:
 | Биссектриса – это линия, делящая угол пополам. |
Биссектриса треугольника — это отрезок биссектрисы угла треугольника, соединяющий вершину этого угла с точкой на противолежащей стороне.
Когда-то древние астрономы и математики открыли очень много интересных свойств биссектрисы. Эти знания сильно упростили жизнь людей.
Стало легче строить, считать расстояния, даже корректировать стрельбу из пушек… Нам же знание этих свойств поможет решить некоторые задания ОГЭ и ЕГЭ!
Первое знание, которое поможет в этом — это…
Биссектриса равнобедренного треугольника
 | Биссектриса равнобедренного треугольника, проведенная к основанию, является и медианой, и высотой. |
Кстати, а помнишь ли ты все эти термины? Помнишь чем они отличаются друг от друга? Нет? Не страшно. Сейчас разберемся.
Итак,
- Основание равнобедренного треугольника – это та сторона, которая не равна никакой другой. Посмотри на рисунок, как ты думаешь, какая это сторона? Правильно — это сторона .
- Медиана – это линия, проведенная из вершины треугольника и делящая противоположную сторону (это снова ) пополам. Заметь, мы не говорим: «Медиана равнобедренного треугольника». А знаешь почему? Потому что медиана, проведенная из вершины треугольника, делит противоположную сторону пополам в ЛЮБОМ треугольнике.
- Высота – это линия, проведенная из вершины и перпендикулярная основанию. Ты заметил? Мы опять говорим о любом треугольнике, а не только о равнобедренном. Высота в ЛЮБОМ треугольнике всегда перпендикулярна основанию.
Итак, разобрались? Ну почти.
Чтобы еще лучше понять и навсегда запомнить что такое биссектриса, медиана и высота, их нужно сравнить друг с другом и понять в чем они похожи и чем они отличаются друг от друга.
При этом, чтобы лучше запомнить, лучше описать все «человеческим языком».
Потом ты легко будешь оперировать языком математики, но сначала ты этот язык не понимаешь и тебе нужно осмыслить все на своем языке.
Итак, в чем они похожи?
Биссектриса, медиана и высота – все они «выходят» из вершины треугольника и упираются в противоположную сторону и «что-то делают» либо с углом из которого выходят, либо с противоположной стороной.
По-моему просто, нет? А чем они отличаются?
Чем отличаются друг от друга биссектриса, медиана и высота?
- Биссектриса делит угол, из которого выходит, пополам.
- Медиана делит противоположную сторону пополам.
- Высота всегда перпендикулярна противоположной стороне.
Теперь все. Понять – легко. А раз понял, можешь запомнить.
Теперь следующий вопрос.
Почему же в случае с равнобедренным треугольником биссектриса оказывается одновременно и медианой и высотой?
Можно просто посмотреть на рисунок и убедиться, что медиана разбивает на два абсолютно равных треугольника.
Вот и все! Но математики не любят верить своим глазам. Им нужно все доказывать.
Страшное слово?
Ничего подобного — все просто! Смотри: у и равны стороны и , сторона у них вообще общая и . ( – биссектриса!) И вот, получилось, что два треугольника имеют по две равные стороны и угол между ними.
Вспоминаем первый признак равенства треугольников (не помнишь, загляни в тему «Треугольник») и заключаем, что , а значит = и .
= – это уже хорошо – значит, оказалась медианой.
А вот что такое ?
Посмотрим на картинку — . А у нас получилось, что . Значит, и тоже! Наконец, ура! и .
Показалось ли тебе это доказательство тяжеловатым? Посмотри на картинку – два одинаковых треугольника говорят сами за себя.
В любом случае твердо запомни:
Биссектриса, проведенная к основанию равнобедренного треугольника, делит это основание пополам и перпендикулярна ему.
Готов дальше?
Теперь сложнее…
Посчитаем угол между биссектрисами в любом треугольнике!
Не бойся, все не так уж хитро. Смотри на рисунок:
 | B проведем две биссектрисы и . Они пересеклись – а куда деваться-то? Какой же угол получился у точки ? |
Давай его посчитаем. Ты помнишь, что сумма углов треугольника равна ?
Применим этот потрясающий факт.
С одной стороны, из :
, то есть .
Теперь посмотрим на :
Но биссектрисы, биссектрисы же!
Значит
, то есть
Вспомним про :
Значит,
Теперь через буквы
Не удивительно ли?
Получилось, что угол между биссектрисами двух углов зависит только от третьего угла!
Ну вот, две биссектрисы мы посмотрели. А что, если их три??!! Пересекутся ли они все в одной точке?

Или будет так?

Как ты думаешь? Вот математики думали-думали и доказали:
Три биссектрисы треугольника (любого!) пересекаются в одной точке – и эта точка – центр вписанной окружности.

Правда, здорово?
Хочешь знать, почему же так получается?
Переходи на следующий уровень – ты готов к покорению новых вершин знаний о биссектрисе!
БИССЕКТРИСА. СРЕДНИЙ УРОВЕНЬ
Биссектриса – это линия, которая делит угол пополам.

Тебе встретилась в задаче биссектриса? Постарайся применить одно (а иногда можешь и несколько) из следующих потрясающих свойств.
1. Биссектриса в равнобедренном треугольнике.
Не боишься слова «теорема»? Если боишься, то – зря. Теоремой математики привыкли называть всякое утверждение, которое можно как-то вывести из других, более простых утверждений.
Так вот, внимание, теорема!
Теорема. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.
Докажем эту теорему, то есть поймём, почему же так получается? Посмотри на равнобедренный .
 | В нём и проведена биссектриса . Видишь: получилось два треугольника . и . |
Давай посмотрим на них внимательно. И тогда увидим, что
- — общая.
А это значит (скорее вспоминай первый признак равенства треугольников!), что .
Ну и что? Хочется тебе так сказать? А то, что мы ещё не смотрели на третьи стороны и оставшиеся углы этих треугольников.
А вот теперь посмотрим. Раз , то совершенно точно и даже вдобавок, .
Вот и получилось, что
- разделила сторону пополам, то есть оказалась медианой
- , а значит, они оба по , так как (глянь ещё раз на рисунок).
Вот и оказалась биссектриса и высотой тоже!
Ура! Доказали теорему. Но представляешь, это ещё не всё. Верна ещё и обратная теорема:
Теорема. Если в треугольнике биссектриса, проведённая из какого-то угла, совпадает с медианой или с высотой, то этот треугольник равнобедренный.
Доказательство? Неужели тебе интересно? Читай следующий уровень теории!
А если неинтересно, то твердо запомни:
Биссектриса совпадает с высотой и медианой только в равнобедренном треугольнике!
Зачем же это твердо запоминать? Как это может помочь? А вот представь, что у тебя задача:
Дано: .
Найти: .

Ты тут же соображаешь, биссектриса и, о чудо, она разделила сторону пополам! (по условию…). Если ты твердо помнишь, что так бывает только в равнобедренном треугольнике, то делаешь вывод, что и значит, пишешь ответ: . Здорово, правда? Конечно, не во всех задачах будет так легко, но знание обязательно поможет!
А теперь следующее свойство. Готов?
2. Биссектриса угла – геометрическое место точек, равноудалённых от сторон угла.
Испугался? На самом деле ничего страшного. Ленивые математики в двух строчках спрятали четыре. Итак, что же значит, «Биссектриса – геометрическое место точек»? А это значит, что выполняются сразу дваутверждения:
- Если точка лежит на биссектрисе, то расстояния от неё до сторон угла равны.
- Если у какой-нибудь точки расстояния до сторон угла равны, то эта точка обязательно лежит на биссектрисе.
Видишь разницу между утверждениями 1 и 2? Если не очень, то вспомни Шляпника из «Алисы в стране чудес»: «Так ты еще чего доброго скажешь, будто «Я вижу то, что ем» и «Я ем то, что вижу», — одно и то же!»
Итак, нам нужно доказать утверждения 1 и 2, и тогда утверждение: «биссектриса – это геометрическое место точек, равноудаленных от сторон угла» будет доказано!
Почему же верно 1?
Возьмём любую точку на биссектрисе и назовём её .

Опустим из этой точки перпендикуляры и на стороны угла.

А теперь …приготовились вспоминать признаки равенства прямоугольных треугольников! Если ты их подзабыл, то загляни в раздел «Прямоугольный треугольник».
Итак…два прямоугольных треугольника: и . У них:
- Общая гипотенуза .
- (потому что – биссектриса!)
Значит, — по углу и гипотенузе. Поэтому и соответствующие катеты у этих треугольников – равны! То есть .
Доказали, что точка одинаково (или равно) удалена от сторон угла. С пунктом 1 разобрались. Теперь перейдём к пункту 2.
Почему же верно 2?
 | Возьмем какую-то точку внутри угла, для которой расстояние до сторон угла равны. |
И соединим точки и .
 | Теперь как прямоугольные по катету и гипотенузе. |
Значит, , то есть лежит на биссектрисе!
Вот и всё!
Как же все это применить при решении задач? Вот например, в задачах часто бывает такая фраза: «Окружность касается сторон угла….». Ну, и найти нужно что-то.
То быстро соображаешь, что
 |
|
И можно пользоваться равенством .
3. Три биссектрисы в треугольнике пересекаются в одной точке
Из свойства биссектрисы быть геометрическим местом точек, равноудаленных от сторон угла, вытекает следующее утверждение:
Три биссектрисы в треугольнике пересекаются в одной точке, и эта точка – центр вписанной в треугольник окружности.
Как именно вытекает? А вот смотри: две-то биссектрисы точно пересекутся, правда?

А третья биссектриса могла бы пройти так:

Но на самом деле-то всё гораздо лучше!
Давай рассмотрим точку пересечения двух биссектрис. Назовём её .
 | Эта точка лежит на биссектрисе . Что из этого следует? Правильно! ! Точка лежит ещё и на биссектрисе , поэтому . |
Что мы тут оба раза применяли? Да пункт 1, конечно же! Если точка лежит на биссектрисе, то она одинаково удалена от сторон угла.
Вот и получилось и .
Но посмотри внимательно на эти два равенства! Ведь из них следует, что и, значит, .
А вот теперь в дело пойдёт пункт 2: если расстояния до сторон угла равны, то точка лежит на биссектрисе…какого же угла? Ещё раз смотри на картинку:
и – расстояния до сторон угла , и они равны, значит, точка лежит на биссектрисе угла . Третья биссектриса прошла через ту же точку! Все три биссектрисы пересеклись в одной точке! И, как дополнительный подарок —
— радиусы вписанной окружности.
(Для верности посмотри ещё тему «Вписанная окружность»).
Ну вот, теперь ты никогда не забудешь:
Точка пересечения биссектрис треугольника – центр вписанной в неё окружности.
Переходим к следующему свойству… Ух и много же свойств у биссектрисы, правда? И это здорово, потому что, чем больше свойств, тем больше инструментов для решения задач про биссектрису.
4. Биссектриса и параллельность, биссектрисы смежных углов
Тот факт, что биссектриса делит угол пополам, в каких-то случаях приводит к совершенно неожиданным результатам. Вот, например,
Случай 1
Биссектриса угла параллелограмма отсекает равнобедренный треугольник.

Здорово, правда? Давай поймём, почему так.
С одной стороны, — мы же проводим биссектрису!
Но, с другой стороны, — как накрест лежащие углы (вспоминаем тему «Параллельные прямые»).
И теперь выходит, что ; выкидываем середину: !
