Какое свойство десятичных дробей

14 августа 2011
Из множества дробей, встречающихся в арифметике, отдельного внимания заслуживают такие, у которых в знаменателе стоит 10, 100, 1000 — в общем, любая степень десятки. У этих дробей есть специальное название и форма записи.
Десятичная дробь — это любая числовая дробь, в знаменателе которой стоит степень десятки.
Примеры десятичных дробей:
![]()
Зачем вообще потребовалось выделять такие дроби? Почему для них нужна собственная форма записи? На то есть как минимум три причины:
- Десятичные дроби намного удобнее сравнивать. Вспомните: для сравнения обычных дробей их требуется вычесть друг из друга и, в частности, привести дроби к общему знаменателю. В десятичных дробях ничего подобного не требуется;
- Сокращение вычислений. Десятичные дроби складываются и умножаются по собственным правилам, и после небольшой тренировки вы будете работать с ними намного быстрее, чем с обычными;
- Удобство записи. В отличие от обычных дробей, десятичные записываются в одну строчку без потери наглядности.
Большинство калькуляторов также дают ответы именно в десятичных дробях. В некоторых случаях другой формат записи может привести к проблемам. Например, что, если потребовать в магазине сдачу в размере 2/3 рубля 🙂
Правила записи десятичных дробей
Основное преимущество десятичных дробей — удобная и наглядная запись. А именно:
Десятичная запись — это форма записи десятичных дробей, где целая часть отделяется от дробной с помощью обычной точки или запятой. При этом сам разделитель (точка или запятая) называется десятичной точкой.
Например, 0,3 (читается: «ноль целых, 3 десятых»); 7,25 (7 целых, 25 сотых); 3,049 (3 целых, 49 тысячных). Все примеры взяты из предыдущего определения.
На письме в качестве десятичной точки обычно используется запятая. Здесь и далее на всем сайте тоже будет использоваться именно запятая.
Чтобы записать произвольную десятичную дробь в указанной форме, надо выполнить три простых шага:
- Выписать отдельно числитель;
- Сдвинуть десятичную точку влево на столько знаков, сколько нулей содержит знаменатель. Считать, что изначально десятичная точка стоит справа от всех цифр;
- Если десятичная точка сдвинулась, а после нее в конце записи остались нули, их надо зачеркнуть.
Бывает, что на втором шаге у числителя не хватает цифр для завершения сдвига. В этом случае недостающие позиции заполняются нулями. Да и вообще, слева от любого числа можно без ущерба для здоровья приписывать любое количество нулей. Это некрасиво, но иногда полезно.
На первый взгляд, данный алгоритм может показаться довольно сложным. На самом деле все очень и очень просто — надо лишь немного потренироваться. Взгляните на примеры:
Задача. Для каждой дроби укажите ее десятичную запись:
Числитель первой дроби: 73. Сдвигаем десятичную точку на один знак (т.к. в знаменателе стоит 10) — получаем 7,3.
Числитель второй дроби: 9. Сдвигаем десятичную точку на два знака (т.к. в знаменателе стоит 100) — получаем 0,09. Пришлось дописать один ноль после десятичной точки и еще один — перед ней, чтобы не оставлять странную запись вида «,09».
Числитель третьей дроби: 10029. Сдвигаем десятичную точку на три знака (т.к. в знаменателе стоит 1000) — получим 10,029.
Числитель последней дроби: 10500. Снова сдвигаем точку на три знака — получим 10,500. В конце числа образовались лишние нули. Зачеркиваем их — получаем 10,5.
Обратите внимание на два последних примера: числа 10,029 и 10,5. Согласно правилам, нули справа надо зачеркнуть, как это сделано в последнем примере. Однако ни в коем случае нельзя поступать так с нулями, стоящими внутри числа (которые окружены другими цифрами). Именно поэтому мы получили 10,029 и 10,5, а не 1,29 и 1,5.
Итак, с определением и формой записи десятичных дробей разобрались. Теперь выясним, как переводить обычные дроби в десятичные — и наоборот.
Переход от обычных дробей к десятичным
Рассмотрим простую числовую дробь вида a/b. Можно воспользоваться основным свойством дроби и умножить числитель и знаменатель на такое число, чтобы внизу получилась степень десятки. Но прежде, чем это делать, прочитайте следующее:
Существуют знаменатели, которые не приводятся к степени десятки. Учитесь распознавать такие дроби, потому что с ними нельзя работать по алгоритму, описанному ниже.
Вот такие дела. Ну и как понять, приводится знаменатель к степени десятки или нет?
Ответ прост: разложите знаменатель на простые множители. Если в разложении присутствуют только множители 2 и 5, это число можно привести к степени десятки. Если найдутся другие числа (3, 7, 11 — что угодно), о степени десятки можно забыть.
Задача. Проверить, можно ли представить указанные дроби в виде десятичных:
Выпишем и разложим на множители знаменатели этих дробей:
20 = 4 · 5 = 22 · 5 — присутствуют только числа 2 и 5. Следовательно, дробь можно представить в виде десятичной.
12 = 4 · 3 = 22 · 3 — есть «запретный» множитель 3. Дробь не представима в виде десятичной.
640 = 8 · 8 · 10 = 23 · 23 · 2 · 5 = 27 · 5. Все в порядке: кроме чисел 2 и 5 ничего нет. Дробь представима в виде десятичной.
48 = 6 · 8 = 2 · 3 · 23 = 24 · 3. Снова «всплыл» множитель 3. Представить в виде десятичной дроби нельзя.
Итак, со знаменателем разобрались — теперь рассмотрим весь алгоритм перехода к десятичным дробям:
- Разложить знаменатель исходной дроби на множители и убедиться, что она вообще представима в виде десятичной. Т.е. проверить, чтобы в разложении присутствовали только множители 2 и 5. Иначе алгоритм не работает;
- Сосчитать, сколько двоек и пятерок присутствует в разложении (других чисел там уже не будет, помните?). Подобрать такой дополнительный множитель, чтобы количество двоек и пятерок сравнялось.
- Собственно, умножить числитель и знаменатель исходной дроби на этот множитель — получим искомое представление, т.е. в знаменателе будет стоять степень десятки.
Разумеется, дополнительный множитель тоже будет разлагаться только на двойки и пятерки. При этом, чтобы не усложнять себе жизнь, следует выбирать наименьший такой множитель из всех возможных.
И еще: если в исходной дроби присутствует целая часть, обязательно переведите эту дробь в неправильную — и только затем применяйте описанный алгоритм.
Задача. Перевести данные числовые дроби в десятичные:
Разложим на множители знаменатель первой дроби: 4 = 2 · 2 = 22. Следовательно, дробь представима в виде десятичной. В разложении присутствуют две двойки и ни одной пятерки, поэтому дополнительный множитель равен 52 = 25. С ним количество двоек и пятерок сравняется. Имеем:
![]()
Теперь разберемся со второй дробью. Для этого заметим, что 24 = 3 · 8 = 3 · 23 — в разложении присутствует тройка, поэтому дробь не представима в виде десятичной.
Две последних дроби имеют знаменатели 5 (простое число) и 20 = 4 · 5 = 22 · 5 соответственно — везде присутствуют только двойки и пятерки. При этом в первом случае «для полного счастья» не хватает множителя 2, а во втором — 5. Получаем:
![]()
Переход от десятичных дробей к обычным
Обратное преобразование — от десятичной формы записи к обычной — выполняется намного проще. Здесь нет ограничений и специальных проверок, поэтому перевести десятичную дробь в классическую «двухэтажную» можно всегда.
Алгоритм перевода следующий:
- Зачеркните все нули, стоящие в десятичной дроби слева, а также десятичную точку. Это будет числитель искомой дроби. Главное — не переусердствуйте и не зачеркните внутренние нули, окруженные другими цифрами;
- Подсчитайте, сколько знаков стоит в исходной десятичной дроби после запятой. Возьмите цифру 1 и припишите справа столько нулей, сколько знаков вы насчитали. Это будет знаменатель;
- Собственно, запишите дробь, числитель и знаменатель которой мы только что нашли. По возможности, сократите. Если в исходной дроби присутствовала целая часть, сейчас мы получим неправильную дробь, что очень удобно для дальнейших вычислений.
Задача. Перевести десятичные дроби в обычные: 0,008; 3,107; 2,25; 7,2008.
Зачеркнем нули слева и запятые — получим следующие числа (это будут числители): 8; 3107; 225; 72008.
В первой и во второй дробях после запятой стоит по 3 знака, во второй — 2, а в третьей — целых 4 знака. Получим знаменатели: 1000; 1000; 100; 10000.
Наконец, объединим числители и знаменатели в обычные дроби:
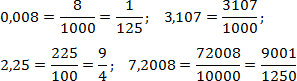
Как видно из примеров, полученную дробь очень часто можно сократить. Еще раз отмечу, что любая десятичная дробь представима в виде обычной. Обратное преобразование можно выполнить не всегда.
Смотрите также:
- Как представить обычную дробь в виде десятичной

- Сложение и вычитание десятичных дробей

- Пробный ЕГЭ 2012. Вариант 3 (без логарифмов)

- Площади многоугольников на координатной сетке

- Специфика работы с логарифмами в задаче B15

- Семинар по задачам B10: теория вероятностей

Десяти́чная дробь — разновидность дроби, которая представляет собой способ представления действительных чисел в виде
где
— знак дроби: либо , либо ,
— десятичная запятая, служащая разделителем между целой и дробной частью числа (стандарт стран СНГ)[1],
— десятичные цифры. Причём последовательность цифр до запятой (слева от неё) конечна (как минимум одна цифра), а после запятой (справа от неё) — может быть как конечной (в частности, цифры после запятой могут вообще отсутствовать), так и бесконечной.
Примеры:
Значением десятичной дроби является действительное число
равное сумме конечного или бесконечного числа слагаемых.
Представление действительных чисел с помощью десятичных дробей является обобщением записи целых чисел в десятичной системе счисления. В представлении целого числа в виде десятичной дроби отсутствуют цифры после запятой, и таким образом, это представление имеет вид
что совпадает с записью этого числа в десятичной системе счисления.
Конечные и бесконечные десятичные дроби[править | править код]
Конечные дроби[править | править код]
Десятичная дробь называется конечной, если она содержит конечное число цифр после запятой (в частности, ни одного), то есть имеет вид
В соответствии с определением эта дробь представляет число
Легко видеть, что это число можно представить в виде обыкновенной дроби вида , знаменатель которой является степенью десятки. Обратно, любое число вида , где — целое, а — целое неотрицательное, можно записать в виде конечной десятичной дроби.
Если обыкновенную дробь привести к несократимому виду, её знаменатель будет иметь вид . Таким образом, имеет место следующая теорема о представимости действительных чисел в виде конечных десятичных дробей.
Теорема. Действительное число представимо в виде конечной десятичной дроби тогда и только тогда, когда оно является рациональным и при записи его несократимой дробью знаменатель не имеет простых делителей, отличных от и .
Бесконечные дроби[править | править код]
Бесконечная десятичная дробь
представляет, согласно определению, действительное число
Этот ряд сходится, каковы бы ни были целое неотрицательное и десятичные цифры . Это предложение вытекает из того факта, что данный ряд мажорируется сходящимся рядом
Представление действительных чисел десятичными дробями[править | править код]
Таким образом, всякая конечная или бесконечная десятичная дробь представляет некоторое вполне определённое действительное число. Остаются следующие вопросы:
- Всякое ли действительное число может быть представлено в виде десятичной дроби?
- Единственно ли такое представление?
- Каков алгоритм разложения числа в десятичную дробь?
Эти вопросы освещаются ниже.
Алгоритм разложения числа в десятичную дробь[править | править код]
Ниже описывается алгоритм построения по произвольному действительному числу десятичной дроби, которая является его представлением.
Рассмотрим вначале случай . Разделим всю числовую прямую целочисленными точками на отрезки единичной длины. Рассмотрим тот отрезок , который содержит точку ; в частном случае, когда точка является концом двух соседних отрезков, в качестве выберем правый отрезок.
Если обозначить целое неотрицательное число, являющееся левым концом отрезка , через , то можно записать:
На следующем шаге разделим отрезок на десять равных частей точками
и рассмотрим тот из отрезков длины , на котором лежит точка ; в случае когда эта точка является концом двух соседних отрезков, из этих двух отрезков опять выберем правый.
Обозначим этот отрезок . Он имеет вид:
Будем продолжать аналогичным образом процесс измельчения числовой прямой и последовательного уточнения положения точки .
На очередном шаге, имея отрезок , содержащий точку , мы делим его на десять равных отрезков и выбираем из них тот отрезок , на котором лежит точка ; в случае когда эта точка является концом двух соседних отрезков, из этих двух отрезков выбираем правый.
Продолжая этот процесс мы получим последовательность отрезков вида
где — целое неотрицательное, а — целые числа, удовлетворяющие неравенству .
Построенная последовательность отрезков обладает следующими свойствами:
Из этих условий следует, что есть система вложенных отрезков, длины которых стремятся к нулю при , а точка есть общая точка всех отрезков системы. Отсюда вытекает, что последовательность левых концов отрезков сходится к точке (аналогичное утверждение справледливо и для последовательности правых концов), то есть
при
Это значит, что ряд
сходится к числу , и таким образом, десятичная дробь
является представлением числа . Таким образом, найдено разложение неотрицательного числа в десятичную дробь.
Полученная десятичная дробь является бесконечной по построению. При этом может оказаться, что начиная с некоторого номера, все десятичные знаки после запятой суть нули, то есть дробь имеет вид
Нетрудно видеть, что эта возможность имеет место в том случае, когда на некотором шаге точка совпадает с одной из точек деления числовой прямой. В этом случае отбрасывая в сумме
нулевые слагаемые, получим, что число также может быть представлено конечной десятичной дробью
Вообще, ясно, что приписывая в конец десятичной дроби после запятой любое количество нулей (в том числе бесконечное), мы не изменяем значение дроби. Таким образом, в данном случае число может быть представлено как конечной, так и бесконечной десятичной дробью (полученной из первой приписыванием бесконечного числа нулей).
Тем самым рассмотрен случай неотрицательного . В случае отрицательного , в качестве десятичного представления этого числа можно взять представление противоположного ему положительного числа, взятое со знаком «минус».
Приведенный алгоритм дает способ разложения произвольного действительного числа в десятичную дробь. Тем самым доказана следующая
Теорема. Всякое действительное число может быть представлено в виде десятичной дроби.
О роли аксиомы Архимеда[править | править код]
Приведенный алгоритм разложения действительного числа в десятичную дробь существенно опирается на свойство системы действительных чисел, называемое аксиомой Архимеда.
Это свойство было использовано дважды в алгоритме. В самом начале построения выбиралось целое , такое, что действительное число находится между и следующим целым :
Однако существование такого целого числа надо ещё доказать: нельзя исключать, например, возможность, когда, каково бы ни было целое , всегда имеет место неравенство . Если бы этот случай имел место, то, очевидно, нужного числа не нашлось бы.
Эта возможность как раз исключается аксиомой Архимеда, согласно которой каково бы ни было число , всегда найдётся целое такое, что . Теперь среди чисел возьмём наименьшее, обладающее свойством . Тогда
Искомое число найдено: .
Второй раз аксиома Архимеда неявно использовалась при доказательстве стремления к нулю длин отрезков последовательности :
Строгое доказательство данного предложения опирается на аксиому Архимеда. Докажем эквивалентное соотношение
В соответствии с аксиомой Архимеда, каково бы ни было действительное число , последовательность натуральных чисел превзойдёт его, начиная с некоторого номера. А поскольку для всякого имеет место неравенство
то последовательность также превзойдёт , начиная с того же номера. В соответствии с определением предела числовой последовательности, это означает, что .
Неоднозначность представления в виде десятичной дроби[править | править код]
С помощью приведённого алгоритма мы можем для любого действительного числа построить десятичную дробь, представляющую данное число. Однако может случиться, что это же самое число может быть представлено в виде десятичной дроби и другим образом.
Неединственность представления чисел в виде десятичных дробей уже следует из того тривиального факта, что, приписывая конечной дроби справа после запятой нули, мы будем получать формально различные десятичные дроби, представляющие одно и то же число.
Однако, если даже считать дроби, полученные путём приписывания в конец друг другу конечного или бесконечного количества нулей, тождественными, представление некоторых действительных чисел всё же остаётся неединственным.
Рассмотрим например, десятичную дробь
Согласно определению, эта дробь является представлением числа . Вместе с тем, это число может быть также представлено в виде десятичной дроби . В самом деле, вещественные числа различны тогда и только тогда, когда между ними можно вставить ещё одно вещественное число, не совпадающее с самими Но между и никакого третьего числа вставить нельзя.
Этот пример можно обобщить. Можно показать, что дроби
и
где , представляют одно и то же действительное число.
Оказывается, этим общим примером исчерпываются все случаи неоднозначности представления действительных чисел в виде десятичных дробей. При этом мы, конечно, не рассматриваем тривиальные случаи дробей, полученные приписыванием нулей в конец друг другу, а также пару дробей и .
Эти результаты можно суммировать в следующей теореме.
Теорема. Всякое действительное число , не представимое в виде , где — целое, — целое неотрицательное, допускает единственное представление в виде десятичной дроби; при этом эта дробь является бесконечной.
Всякое действительное число вида может быть представлено в виде десятичной дроби более чем одним способом. Если , то оно может быть представлено как в виде конечной десятичной дроби, а также бесконечной дроби, полученной приписыванием нулей в конец после запятой, так и в виде бесконечной дроби, оканчивающейся на . Число может быть представлено дробями вида , а также дробями вида .
Замечание. Бесконечные дроби, оканчивающиеся на , получаются, если в приведённом выше алгоритме всегда выбирать левый отрезок вместо правого.
Лишние нули и погрешность[править | править код]
Следует отметить, что, с точки зрения приближённых вычислений, запись десятичной дроби с нулями в конце не совсем тождественна записи без этих нулей.
Принято считать, что, если погрешность не указана, то абсолютная погрешность десятичной дроби равна половине единицы последнего выписанного разряда, т.е. число получено в соответствии с правилами округления[2]. Например, запись «3,7» означает, что абсолютная погрешность равна 0,05. А в записи «3,700» абсолютная погрешность равна 0,0005.
Другие примеры:
- «25» — абсолютная погрешность равна 0,5 (также такая запись может означать точное значение 25: например, 25 штук);
- «2,50∙10⁴» — абсолютная погрешность равна 50;
- «25,00» — абсолютная погрешность равна 0,005.
Периодические десятичные дроби[править | править код]
Бесконечная десятичная дробь называется периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр. Другими словами, периодическая дробь — десятичная дробь, имеющая вид
Такую дробь принято кратко записывать в виде
Повторяющаяся группа цифр называется периодом дроби, количество цифр в этой группе — длиной периода.
Если в периодической дроби период следует сразу после запятой, то дробь называется чистой периодической. Если же между запятой и первым периодом имеются цифры, дробь называется смешанной периодической, а группа цифр после запятой до первого знака периода — предпериодом дроби. Например, дробь является чистой периодической, а дробь — смешанной периодической.
Основное свойство периодических дробей, благодаря которому их выделяют из всей совокупности десятичных дробей, заключается в том, что периодические дроби и только они представляют рациональные числа. Точнее, имеет место следующее предложение.
Теорема. Всякая бесконечная периодическая десятичная дробь представляет рациональное число. Обратно, если рациональное число раскладывается в бесконечную десятичную дробь, то эта дробь является периодической.
Можно показать, что чисто периодические дроби соответствуют рациональным числам, в записи которых в виде несократимой дроби знаменатель не имеет простых делителей и , а также рациональным числам , у которых знаменатель имеет только простые делители и . Соответственно, смешанные периодические дроби соответствуют несократимым дробям , знаменатель которых имеет как простые делители или , так и отличные от них.
Перевод из десятичной дроби в обыкновенную[править | править код]
Предположим, что дана периодическая десятичная дробь с периодом 4. Заметим, что домножив её на , получим большую дробь с теми же цифрами после запятой. Отняв целую часть (), на которую увеличилась дробь после её умножения, получаем исходную дробь ()[3]:
Произношение десятичных дробей[править | править код]
В русском языке десятичные дроби читаются так: сначала произносится целая часть, потом слово «целых» (или «целая»), потом дробная часть так, как если бы всё число состояло только из этой части, то есть числитель дроби — количественное числительное женского рода (одна, две, восемь и т.д.), а знаменатель — порядковое числительное (десятая, сотая, тысячная, десятитысячная и т.д.).
Например: 5,45 — пять целых, сорок пять сотых.
Для более длинных чисел иногда десятичную часть разбивают по степеням тысячи.
Например: 0,123 456 — ноль целых, сто двадцать три тысячных, четыреста пятьдесят шесть миллионных.
Однако на практике часто как более рациональное, превалирует такое произношение: целая часть, союз «и» (часто опускается), дробная часть.
Например: 5,45 — пять и сорок пять; (пять-сорок пять).
Для периодических десятичных дробей произносят часть числа до периода (выраженную целым числом в случае чистой периодической дроби или конечной десятичной дробью в случае смешанной периодической дроби), а затем добавляют число в периоде.
Например: 0,1(23) — ноль целых, одна десятая и двадцать три в периоде; 2,(6) — две целых и шесть в периоде.
История[править | править код]
Десятичные дроби впервые встречаются в Китае примерно с III века н. э. при вычислениях на счётной доске (суаньпань). В письменных источниках десятичные дроби ещё некоторое время изображали в традиционном (не позиционном) формате, но постепенно позиционная система вытеснила традиционную[4].
Тимуридский математик и астроном Джамшид Гияс-ад-дин аль-Каши (1380—1429) в трактате «Ключ арифметики» объявил себя изобретателем десятичных дробей, хотя они встречались в трудах Ал-Уклидиси, жившего на 5 веков раньше[5].
В Европе первоначально десятичные дроби записывали как целые числа в некотором оговоренном масштабе; например, тригонометрические таблицы Региомонтана (1467) содержали значения, увеличенные в 100000 раз и затем округлённые до целого. Первые десятичные дроби в Европе ввёл Иммануил Бонфис около 1350 года, в 1579 году их употребление пытался пропагандировать Виет. Но широкое распространение они получили только после появления сочинения Симона Стевина «Десятая» (1585)[6].
См. также[править | править код]
- Десятичный разделитель
- Десятичная система счисления
- Обыкновенная дробь
- Непрерывная дробь
Примечания[править | править код]
- ↑ Знак запятой «» — десятичная запятая (англ. decimal comma) — как разделитель целой и дробной частей десятичной дроби принят в России, европейских странах (кроме Великобритании и Ирландии) и многих других странах, на которые они имели культурное влияние. В англоязычных странах и странах, на которые они имели влияние, для этого используется знак точки «» — десятичная точка (англ. decimal point), а знак запятой используется для группировки цифр целой части числа по три десятичных разряда (так называемый разделитель групп разрядов, в России для этого используется знак неразрывного пробела « »). Например, дробь в десятичной записи в российском стандарте будет выглядеть так: , а в английском стандарте так: . Подробнее см. Десятичный разделитель.
- ↑ Выгодский М. Я. Справочник по элементарной математике. — М.: Государственное издательство технико-теоретической литературы, 1954. — 412 с.
- ↑ Энциклопедия для детей. — М.: Аванта+, 2001. — Т. 11. Математика. — ISBN 5-8483-0015-1., страница 179
- ↑ Jean-Claude Martzloff. A History of Chinese Mathematics. Springer. 1997. ISBN 3-540-33782-2.
- ↑ Berggren J. Lennart. Mathematics in Medieval Islam // The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. — Princeton: Princeton University Press, 2007. — С. 518. — ISBN 978-0-691-11485-9.
- ↑ Гутер Р. С., Полунов Ю. Л. Джон Непер, 1550—1617. — М.: Наука, 1980. — С. 197—204. — 226 с. — (Научно-биографическая литература).
Ссылки[править | править код]
- ЕГЭ математика. Периодическая дробь
- Задачи по теме «обыкновенные и десятичные дроби»
- Семёнова Л. Периодические дроби.
