Какое основное свойство дроби

В данной статье разберем, в чем заключается основное свойство дроби, сформулируем его, приведем доказательство и наглядный пример. Затем рассмотрим, как применять основное свойство дроби при совершении действий сокращения дробей и приведения дробей к новому знаменателю.
Основное свойство дроби, формулировка, доказательство и примеры
Все обыкновенные дроби обладают важнейшим свойством, которое мы и называем основным свойством дроби, и звучит оно следующим образом:
Определение 1
Если числитель и знаменатель одной дроби умножить или разделить на одно и то же натуральное число, то в итоге получится дробь, равная заданной.
Представим основное свойство дроби в виде равенства. Для натуральных чисел a, b и mбудут справедливыми равенства:
a·mb·m=ab и a:mb:m=ab
Рассмотрим доказательство основного свойства дроби. Опираясь на свойства умножения натуральных чисел и свойства деления натуральных чисел, запишем равенства: (a · m) · b = (b · m) · a и (a : m) · b = (b : m) · a. Таким образом, дроби a·mb·m и ab, а также a:mb:m и ab являются равными по определению равенства дробей.
Разберем пример, который графически проиллюстрирует основное свойство дроби.
Пример 1
Допустим, у нас есть квадрат, разделенный на 9 «больших» частей-квадратов. Каждый «большой» квадрат разделен на 4 меньших по размеру. Возможно сказать, что заданный квадрат поделен на 4·9 = 36 «маленьких» квадратов. Выделим цветом 5 «больших» квадратов. При этом окрашенными будут 4·5 = 20 «маленьких» квадратов. Покажем рисунок, демонстрирующий наши действия:
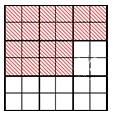
Окрашенная часть – это 59 исходной фигуры или 2036, что является тем же самым. Таким образом, дроби 59 и 2036 являются равными: 59=2036 или 2036=59.
Эти равенства, а также равенства 20 = 4·5, 36 = 4·9, 20:4 = 5 и 36:4 = 9 дают возможность сделать вывод, что 59=5·49·4 и 2036=20·436·4.
Чтобы закрепить теорию, разберем решение примера.
Пример 2
Задано, что числитель и знаменатель некоторой обыкновенной дроби умножили на 47, после чего эти числитель и знаменатель разделили на 3. Равна ли полученная в итоге этих действий дробь заданной?
Решение
Опираясь на основное свойство дроби, можно говорить о том, что умножение числителя и знаменателя заданной дроби на натуральное число 47 даст в результате дробь, равную исходной. То же самое мы можем утверждать, производя дальнейшее деление на 3. В конечном счете мы получим дробь, равную заданной.
Ответ: да, полученная в итоге дробь будет равна исходной.
Применение основного свойства дроби
Основное свойство применяется, когда нужно привести дроби к новому знаменателю и при сокращении дробей.
Приведение дроби к новому знаменателю – это действие замены заданной дроби равной ей дробью, но с большими числителем и знаменателем. Чтобы привести дробь к новому знаменателю, нужно умножить числитель и знаменатель дроби на необходимое натуральное число. Действия с обыкновенными дробями были бы невозможны без способа приводить дроби к новому знаменателю.
Определение 2
Сокращение дроби – действие перехода к новой дроби, равной заданной, но с меньшими числителем и знаменателем. Чтобы сократить дробь, нужно разделить числитель и знаменатель дроби на одно и то же необходимое натуральное число, которое будет называться общим делителем.
Возможны случаи, когда подобного общего делителя нет, тогда говорят о том, что исходная дробь несократима или не подлежит сокращению. В частности, сокращение дроби при помощи наибольшего общего делителя приведет дробь к несократимому виду.
Ключевые слова конспекта: дроби, обыкновенная дробь, правильные и неправильные дроби, основное свойство дроби, сравнение дробей, арифметические действия с дробями, нахождение части от целого и целого по его части.
Одна или несколько равных частей единицы называются обыкновенной дробью. Дробь 3/4 означает, что единицу разделили на 4 части и взяли 3 таких части.

Дробь можно рассматривать и как результат деления натуральных чисел. Частное от деления натуральных чисел а и b можно записать в виде дроби a/b — где делимое а — числитель, а делитель b — знаменатель.

Правильная и неправильная дробь
Дробь, в которой числитель меньше знаменателя, называется правильной, а дробь, где числитель больше или равен знаменателю, — неправильной.

Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Для этого нужно умножить целую часть на знаменатель и к произведению прибавить числитель данной дроби. Полученная сумма будет числителем дроби, а знаменателем остается знаменатель дробной части.

Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления — это целая часть, остаток — это числитель, делитель — это знаменатель.

Основное свойство дроби
Определение. Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной.

Основное свойство дроби используют при сокращении дробей. Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дробей.

Сравнение дробей
- Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
- Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
- привести дроби к наименьшему общему знаменателю;
- сравнить полученные дроби.

Чтобы привести дроби к наименьшему общему знаменателю, нужно:
- найти наименьшее общее кратное (НОК) знаменателей дробей (оно и будет их общим знаменателем);
- разделить общий знаменатель на знаменатель данных дробей, т. е. найти для каждой дроби дополнительный множитель;
- умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Арифметические действия с обыкновенными дробями
Сложение и вычитание дробей
При сложении (вычитании) дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель. Полученную дробь, если возможно, сокращают и выделяют целую часть.
При сложении (вычитании) дробей с разными знаменателями нужно предварительно привести эти дроби к наименьшему общему знаменателю, затем сложить (вычесть) полученные дроби, используя правило сложения (вычитания) дробей с одинаковыми знаменателями.

Особенно надо быть внимательным при сложении (вычитании) с участием смешанных чисел!

Общий случай сложения (вычитания) дробей.

Умножение дробей
- Произведение двух дробей a/b и c/d равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

- При умножении чисел, состоящих из целой и дробной частей, их предварительно представляют в виде неправильных дробей, а затем умножают согласно п. 1.

Деление дробей
Два числа называются взаимно обратными, если их произведение равно 1, то есть дроби вида a/b и b/a являются взаимно обратными. Например 1/3 и 3. Чтобы разделить одну дробь на другую, нужно делимое умножить на число, обратное к делителю.

При делении чисел, состоящих из целой и дробной части, нужно предварительно представить их в виде неправильной дроби.

Нахождение части от целого (дроби от числа)
Чтобы найти часть от целого, нужно число, соответствующее целому, разделить на знаменатель дроби, выражающей эту часть, и результат умножить на числитель той же дроби.
Задача нахождения части от целого по существу является задачей нахождения дроби от числа. Чтобы найти дробь (часть) от числа, необходимо число умножить на эту дробь.

Нахождение целого по его части (числа по его дроби)
Чтобы найти целое по его части, нужно число, соответствующее этой части, разделить на числитель дроби, выражающей эту часть, и результат умножить на знаменатель той же дроби.
Задача нахождения целого по его части по существу является задачей нахождения числа по его дроби. Чтобы найти число по его дроби, необходимо данное значение разделить на эту дробь.

Это конспект по теме «Обыкновенная дробь». Выберите дальнейшие действия:
- Перейти к следующему конспекту: Десятичная дробь
- Вернуться к списку конспектов по Математике.
- Проверить знания по Математике.
Первой дробью, с которой познакомились люди, была половина.
Хотя названия всех следующих дробей связаны с названиями их знаменателей («треть», «четверть» и т. д.), для половины это не так — ее название во всех языках не имеет ничего общего со словом «два».
Сегодня мы познакомимся с основным свойством любой из таких дробей.

Возьмем круг, разделим его на три равные части и закрасим две из них.
Каждую из 3-х частей поделим еще на 4 равные части.
Посмотрим, что получилось:

Получим, что весь круг поделен на ( textbf{3}cdottextbf{4}=textbf{12} ) частей, а в двух закрашенных частях круга будет (textbf{2}cdottextbf{4}=textbf{8} ) таких частей.
Значит, $$frac{textbf{2}}{textbf{3}}=frac{textbf{2}cdottextbf{4}}{textbf{3}cdottextbf{4}}=frac{textbf{8}}{textbf{12}}$$
То есть $$frac{textbf{2}}{textbf{3}}=frac{textbf{8}}{textbf{12}} $$
Можно записать иначе:
$$frac{textbf{8}}{textbf{12}}=frac{textbf{8 : 4}}{textbf{12 : 4}}=frac{textbf{2}}{textbf{3}}$$
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
В этом заключается основное свойство дроби.
Две равные дроби являются различными записями одного и того же числа.
У меня есть дополнительная информация к этой части урока!

Закрыть
С дробями можно легко познакомиться в быту. Достаточно вспомнить как выглядят настенные часы.
Там есть разделение на часы, минуты, а стрелки могут показывать, на какие части делится весь циферблат.

При этом мы будем получать дроби со знаменателями 12 (если делим на части по часам) или 60 (если делим на части по минутам).
Например:
$$frac{textbf{1}}{textbf{2}}=frac{textbf{6}}{textbf{12}}=frac{textbf{30}}{textbf{60}}$$
Половина циферблата — это 6 часов из 12 или 30 минут из 60.
Любое математическое правило или свойство можно применить на практике.
Посмотрим, как применяется основное свойство дроби.
Пример:
$$frac{textbf{3}}{textbf{4}}=frac{textbf{x}}{textbf{12}}$$
Решение
Мы видим, что неизвестен числитель второй дроби, но дроби между собой равны.
Значит, используя основное свойство дроби, выясним, во сколько раз отличаются знаменатели дробей.
Проще делить больший знаменатель на меньший.
То есть,
$$frac{textbf{3}}{textbf{4}}=frac{textbf{3}cdottextbf{a}}{textbf{4}cdottextbf{a}}=frac{textbf{x}}{textbf{12}}$$
$$textbf{4}cdottextbf{a}=textbf{12}$$
12 разделим на 4 и получим 3
$$textbf{a}=textbf{3}$$
Теперь найдем неизвестный числитель.
Мы посчитали, что a = 3 Подставив в формулу это значение, получим:
$$textbf{x}=textbf{3}cdottextbf{a}=textbf{3}cdottextbf{3}=textbf{9}$$
Получаем девять в числителе второй дроби:
$$frac{textbf{3}}{textbf{4}}=frac{textbf{9}}{textbf{12}}$$
Здесь видим подтверждение того факта, что равные дроби являются различными записями одного и того же числа.
Пример:
На тетрадном листе начертите луч длиной 10 клеток. Отметьте на нем точки с координатами:
$$frac{textbf{1}}{textbf{2}} ; frac{textbf{4}}{textbf{5}} ; frac{textbf{3}}{textbf{10}}$$
Решение
Начертим луч и отметим нужные нам координаты, используя основное свойство дроби, где это требуется.

$$frac{textbf{1}}{textbf{2}}=frac{textbf{1}cdottextbf{5}}{textbf{2}cdottextbf{5}}=frac{textbf{5}}{textbf{10}}$$
$$frac{textbf{4}}{textbf{5}}=frac{textbf{4}cdottextbf{2}}{textbf{5}cdottextbf{2}}=frac{textbf{8}}{textbf{10}}$$
В русском языке слово «дробь» появилось в VIII веке. Оно происходит от глагола «дробить» — разбивать, ломать на части.
Современное обозначение дробей берет своё начало в Древней Индии, затем его стали использовать и арабы.
В старых руководствах есть следующие названия дробей на Руси:
1/2 — половина, полтина | 1/3 — треть |
1/4 — четь | 1/6 — полтреть |
1/8 — полчеть | 1/12 — полполтреть |
1/16 — полполчеть | 1/24 — полполполтреть (малая треть) |
1/32 — полполполчеть (малая четь) | 1/5 — пятина |
Славянская нумерация употреблялась в России до XVI века, затем в страну начала постепенно проникать десятичная позиционная система счисления, она окончательно вытеснила славянскую нумерацию при Петре I.
Использовалась в России земельная мера четверть и более мелкая — получетверть, которая называлась осьмина.
Это были конкретные дроби, единицы для измерения площади земли. Но осьминой нельзя было измерить время или скорость и др.
Значительно позднее осьмина стала означать отвлеченную дробь 1/8, которой можно выразить любую величину.
О применении дробей в России XVII века можно прочитать в книге В. Беллюстина «Как постепенно люди дошли до настоящей арифметики» следующее:
«В рукописи XVII в. «Статиячисленная о всяких долях указ «начинается прямо с письменного обозначения дробей и с указания числителя и знаменателя.
При выговаривании дробей интересны такие особенности: четвертая часть называлась четью, доли же со знаменателем от 5 до 11 выражались словами с окончанием «ина», так что 1/7— седмина, 1/5— пятина, 1/10— десятина; доли же со знаменателями, большими 10, выговаривались с помощью слов «жеребей», например 5/13— пять тринадцатых жеребьёв.
Нумерация дробей была прямо заимствована из западных источников: числитель назывался «верхним числом», знаменатель «исподним».
Пройти тест

Основное свойство дроби
Если ad=bc, то две дроби frac{a}{b}и frac{c}{d} считаются равными. К примеру, равными будут дроби frac35и frac{9}{15}, так как 3 cdot 15 = 15 cdot 9, frac{12}{7}и frac{24}{14}, так как 12 cdot 14 = 7 cdot 24.
Из определения равенства дробей следует, что равными будут дроби frac{a}{b}и frac{am}{bm}, так как a(bm)=b(am) — наглядный пример применения сочетательного и переместительного свойств умножения натуральных чисел в действии.
Значит frac{a}{b} = frac{am}{bm} — так выглядит основное свойство дроби.
Другими словами, мы получим дробь, равную данной, умножив или разделив числитель и знаменатель исходной дроби на одно и то же натуральное число.
Сокращение дроби — это процесс замены дроби, при котором новая дробь получается равной исходной, но с меньшим числителем и знаменателем.
Сокращать дроби принято, опираясь на основное свойство дроби.
Например, frac{45}{60}=frac{15}{20}(числитель и знаменатель делится на число 3); полученную дробь снова можно сократить, разделив на 5, то есть frac{15}{20}=frac 34.
Несократимая дробь — это дробь вида frac 34, где числитель и знаменатель являются взаимно простыми числами. Основная цель сокращения дроби — сделать дробь несократимой.
Приведение дробей к общему знаменателю
Возьмем в качестве примера две дроби: frac{2}{3}и frac{5}{8} с разными знаменателями 3 и 8. Для того, чтобы привести данные дроби к общему знаменателю и сначала перемножим числитель и знаменатель дроби frac{2}{3}на 8. Получаем следующий результат: frac{2 cdot 8}{3 cdot 8} = frac{16}{24}. Затем умножаем числитель и знаменатель дроби frac{5}{8}на 3. Получаем в итоге: frac{5 cdot 3}{8 cdot 3} = frac{15}{24}. Итак, исходные дроби приведены к общему знаменателю 24.
Арифметические действия над обыкновенными дробями
Сложение обыкновенных дробей
а) При одинаковых знаменателях числитель первой дроби складывают с числителем второй дроби, оставляя знаменатель прежним. Как видно на примере:
frac{a}{b}+frac{c}{b}=frac{a+c}{b};
б) При разных знаменателях дроби сначала приводят к общему знаменателю, а затем выполняют сложение числителей по правилу а):
frac{7}{3}+frac{1}{4}=frac{7 cdot 4}{3}+frac{1 cdot 3}{4}=frac{28}{12}+frac{3}{12}=frac{31}{12}.
Вычитание обыкновенных дробей
а) При одинаковых знаменателях из числителя первой дроби вычитают числитель второй дроби, оставляя знаменатель прежним:
frac{a}{b}-frac{c}{b}=frac{a-c}{b};
б) Если же знаменатели дробей различны, то сначала дроби приводят к общему знаменателю, а затем повторяют действия как в пункте а).
Умножение обыкновенных дробей
Умножение дробей подчиняется следующему правилу:
frac{a}{b} cdot frac{c}{d}=frac{a cdot c}{b cdot d},
то есть перемножают отдельно числители и знаменатели.
Например:
frac{3}{5} cdot frac{4}{8} = frac{3 cdot 4}{5 cdot 8}=frac{12}{40}.
Деление обыкновенных дробей
Деление дробей производят следующим способом:
frac{a}{b} : frac{c}{d}= frac{ad}{bc},
то есть дробь frac{a}{b} умножается на дробь frac{d}{c}.
Пример: frac{7}{2} : frac{1}{8}=frac{7}{2} cdot frac{8}{1}=frac{7 cdot 8}{2 cdot 1}=frac{56}{2}.
Взаимно обратные числа
Если ab=1, то число b является обратным числом для числа a.
Пример: для числа 9 обратным является frac{1}{9}, так как 9 cdot frac{1}{9}=1, для числа 5 — frac{1}{5}, так как 5 cdot frac{1}{5}=1.
Десятичные дроби
Десятичной дробью называется правильная дробь, знаменатель которой равен 10, 1000, 10,000, …, 10^n.
Например: frac{6}{10}=0,6;enspace frac{44}{1000}=0,044.
Таким же способом пишутся неправильные со знаменателем 10^n или смешанные числа.
Например: 5frac{1}{10}=5,1;enspace frac{763}{100}=7frac{63}{100}=7,63.
В виде десятичной дроби представляется любая обыкновенная дробь со знаменателем, который является делителем некой степени числа 10.
Пример: 5 — делитель числа 100, поэтому дробь frac{1}{5}=frac{1 cdot 20}{5 cdot 20}=frac{20}{100}=0,2.
Арифметические действия над десятичными дробями
Сложение десятичных дробей
Для сложения двух десятичных дробей, нужно их расположить так, чтобы друг под другом оказались одинаковые разряды и запятая под запятой, а затем выполнить сложение дробей как обычных чисел.

Вычитание десятичных дробей
Выполняется аналогично сложению.

Умножение десятичных дробей
При умножении десятичных чисел достаточно перемножить заданные числа, не обращая внимания на запятые (как натуральные числа), а в полученном ответе запятой справа отделяется столько цифр, сколько их стоит после запятой в обоих множителях суммарно.
Давайте выполним умножение 2,7 на 1,3. Имеем 27 cdot 13=351. Отделяем справа две цифры запятой (у первого и второго числа — одна цифра после запятой; 1+1=2). В итоге получаем 2,7 cdot 1,3=3,51.
Если в полученном результате получается меньше цифр, чем надо отделить запятой, то впереди пишут недостающие нули, например:

Для умножения на 10, 100, 1000, надо в десятичной дроби перенести запятую на 1, 2, 3 цифры вправо (в случае необходимости справа приписывается определенное число нулей).
Например: 1,47 cdot 10,000 = 14 700.
Деление десятичных дробей
Деление десятичной дроби на натуральное число производят также, как и деление натурального числа на натуральное. Запятая в частном ставится после того, как закончено деление целой части.

Если целая часть делимого меньше делителя, то в ответе получается нуль целых, например:
.png)
Рассмотрим деление десятичной дроби на десятичную. Пусть нужно разделить 2,576 на 1,12. Первым делом, умножим делимое и делитель дроби на 100, то есть перенесем запятую вправо в делимом и делителе на столько знаков, сколько их стоит в делителе после запятой (в данном примере на две). Затем нужно выполнить деление дроби 257,6 на натуральное число 112, то есть задача сводится к уже рассмотренному случаю:
.png)
Бывает так, что не всегда получается конечная десятичная дробь при делении одного числа на другое. В результате получается бесконечная десятичная дробь. В таких случаях переходят к обыкновенным дробям.
2,8 : 0,09= frac{28}{10} : frac {9}{100}= frac{28 cdot 100}{10 cdot 9}=frac{280}{9}=31 frac{1}{9}.
