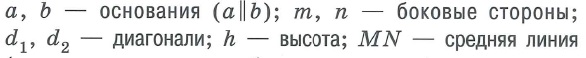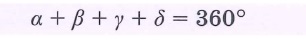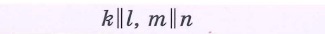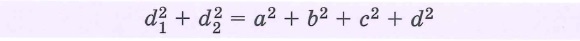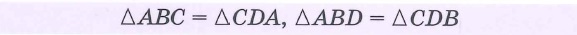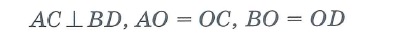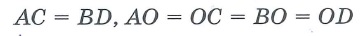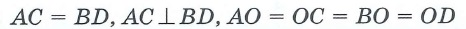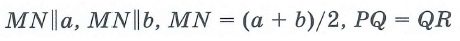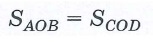Какое общее свойство у квадрата и треугольника

Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. Свойства параллелограмма. Свойства ромба. Свойства прямоугольника. Свойства квадрата. Свойства трапеции. Примерно 7-9 класс (13-15 лет)
Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
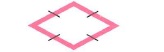
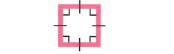
Виды четырехугольников: | |||
|  | ||
|  | ||
|  | ||
|  | ||
|  | ||
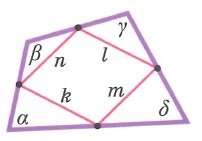
Свойства произвольных четырехугольников: | |||
|  | ||
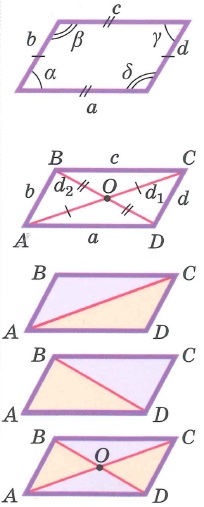
Свойства параллелограмма: | |||
|  | ||
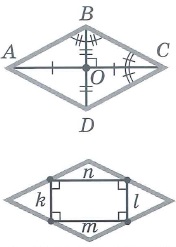
Свойства ромба: | |||
|  | ||
Свойства прямоугольника: | |||
| 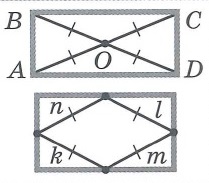 | ||
Свойства квадрата: | |||
|  | ||
Свойства трапеции: | |||
| 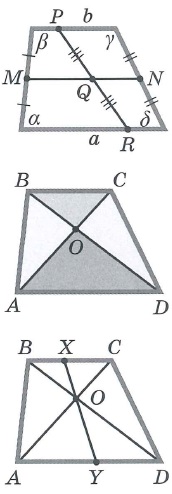 | ||
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers
Консультации и техническая
поддержка сайта: Zavarka Team
Многоугольником называется геометрическая фигура, которая со всех сторон ограничена замкнутой ломаной линией. При этом количество звеньев ломаной не должно быть меньше трех. Каждая пара отрезков ломаной имеет общую точку и образует углы. Количество углов совместно с количеством отрезков ломаной являются основными характеристиками многоугольника. В каждом многоугольнике количество звеньев ограничивающей замкнутой ломаной совпадает с количеством углов.
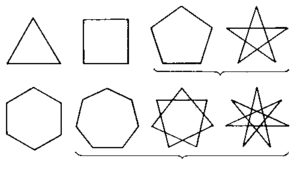
Сторонами в геометрии принято называть звенья ломаной линии, которая ограничивает геометрический объект. Вершинами называют точки соприкосновения двух соседних сторон, по количеству которых получают свои названия многоугольники.
Если замкнутая ломаная состоит из трех отрезков, она носит название треугольника; соответственно, из четырех отрезков — четырехугольником, из пяти — пятиугольником и пр.
Для обозначения треугольника или четырехугольника пользуются заглавными латинскими буквами, обозначающими его вершины. Буквы называют по порядку — по часовой стрелке или против нее.
Основные понятия
Описывая определение многоугольника, следует учитывать некоторые смежные геометрические понятия:
- Если вершины являются концами одной стороны, они называются соседними.
- Если отрезок соединяет между собой несоседние вершины, то он имеет название диагонали. У треугольника не может быть диагоналей.
- Внутренний угол — это угол при одной из вершин, который образован двумя его сторонами, сходящимися в этой точке. Он всегда располагается во внутренней области геометрической фигуры. Если многоугольник невыпуклый, его размер может превосходить 180 градусов.
- Внешний угол при определенной вершине — это угол смежный с внутренним при ней же. Иными словами, внешним углом можно считать разность между 180° и величиной внутреннего угла.
- Сумма величин всех отрезков носит название периметра.
- Если все стороны и все углы равны — он носит название правильного. Правильными могут быть только выпуклые.
Как уже упоминалось выше, названия многоугольных геометрических строятся исходя из количества вершин. Если у фигуры их количество равняется n, она носит название n-угольника:
- Многоугольник называется плоским, если ограничивает конечную часть плоскости. Эта геометрическая фигура может быть вписанной в окружность или описанной вокруг окружности.
- Выпуклым называется n-угольник, который соответствует одному из условий, приведенных ниже.
- Фигура расположена по одну сторону от прямой линии, которая соединяет две соседних вершины.
- Эта фигура служит общей частью или пересечением нескольких полуплоскостей.
- Диагонали располагаются внутри многоугольника.
- Если концы отрезка располагаются в точках, которые принадлежат многоугольнику, весь отрезок принадлежит ему.
- Фигура может называться правильной, если у нее все отрезки и все углы равны. Примерами могут служить квадрат, равносторонний треугольник или правильный пятиугольник.
- Если n-угольник невыпуклый, все стороны и углы его равны, а вершины совпали с таковыми правильного n-угольника, он называется звездчатым. У таких фигур могут иметься самопересечения. Примерами могут служить пентаграмма или гексаграмма.
- Треугольник или четырехугольник называется вписанным в окружность, когда все его вершины располагаются внутри одной окружности. Если же стороны этой фигуры имеют точки соприкосновения с окружностью, это многоугольник описанным около некоторой окружности.
Любой выпуклый n-угольник можно поделить на треугольники. При этом количество треугольников бывает меньше количества сторон на 2.
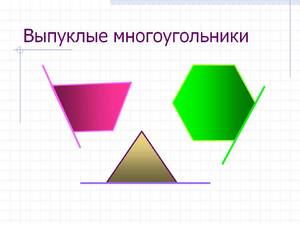
Виды фигур
Треугольник
Это многоугольник с тремя вершинами и тремя отрезками, соединяющими их. При этом точки соединения отрезков не лежат на одной прямой.
Точки соединения отрезков — это вершины треугольника. Сами отрезки называются сторонами треугольника. Общая сумма внутренних углов каждого треугольника равняется 180°.
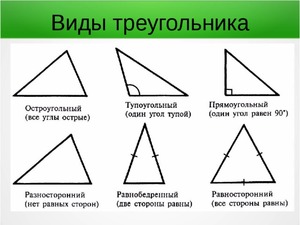
По соотношениям между сторонами все треугольники можно подразделять на несколько видов:
- Равносторонние — у которых длина всех отрезков одинаковая.
- Равнобедренные — треугольники, у которых равны два отрезка из трех.
- Разносторонние — если длина всех отрезков разная.
Кроме того, принято различать следующие треугольники:
- Остроугольные.
- Прямоугольные.
- Тупоугольные.
Четырехугольник
Четырехугольником называется плоская фигура, имеющая 4 вершины и 4 отрезка, которые их последовательно соединяют.
- Если все углы четырехугольника прямые — эта фигура называется прямоугольником.
- Прямоугольник, у которого все стороны имеют одинаковую величину, называется квадратом.
- Четырехугольник, все стороны которого равны, называется ромбом.
На одной прямой не может находиться сразу три вершины четырехугольника.
Видео
Дополнительную информацию о многоугольниках вы найдете в этом видео.
Êâàäðàò — ïðàâèëüíûé ÷åòûð¸õóãîëüíèê. Ó êâàäðàòà âñå óãëû è ñòîðîíû îäèíàêîâû.
Êâàäðàòû ðàçëè÷àþòñÿ ëèøü äëèíîé ñòîðîíû, à âñå 4 óãëà ïðÿìûå è ðàâíû 90°.
Êâàäðàòîì ìîæåò ñòàòü ïàðàëëåëîãðàìì, ðîìá ëèáî ïðÿìîóãîëüíèê, êîãäà ó íèõ îäèíàêîâûå äëèíû äèàãîíàëåé, ñòîðîí è ðàâíûå óãëû.


Ñâîéñòâà êâàäðàòà.
— ó âñåõ 4-õ ñòîðîí êâàäðàòà îäèíàêîâàÿ äëèíà, ò.å. ñòîðîíû êâàäðàòà ðàâíû:
AB = BC = CD = AD
— ïðîòèâîëåæàùèå ñòîðîíû êâàäðàòà ïàðàëëåëüíû:
AB||CD, BC||AD
— êàæäûé óãîë êâàäðàòà ïðÿìîé:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
— ñóììà óãëîâ êâàäðàòà ðàâíà 360°:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
— êàæäàÿ äèàãîíàëü êâàäðàòà èìååò òàêóþ æå äëèíó, êàê è äðóãàÿ:
AC = BD
— êàæäàÿ èç äèàãîíàëåé êâàäðàòà äåëèò êâàäðàò íà 2 îäèíàêîâûå ñèììåòðè÷íûå ôèãóðû.
— óãîë ïåðåñå÷åíèÿ äèàãîíàëåé êâàäðàòà ðàâåí 90°, ïåðåñåêàÿ äðóã äðóãà, äèàãîíàëè äåëÿòñÿ íà äâå ðàâíûå ÷àñòè:
AC┴BD;AO = BO = CO = DO = d/2
— òî÷êó ïåðåñå÷åíèÿ äèàãîíàëåé íàçûâàþò öåíòð êâàäðàòà è îíà îêàçûâàåòñÿ öåíòðîì âïèñàííîé è îïèñàííîé îêðóæíîñòåé.
— âñå äèàãîíàëè äåëÿò óãîë êâàäðàòà íà äâå ðàâíûå ÷àñòè, òàêèì îáðàçîì, îíè îêàçûâàþòñÿ áèññåêòðèñàìè óãëîâ êâàäðàòà:
ΔABC = ΔADC = ΔBAD = ΔBCD
∠ACB = ∠ACD = ∠BDC = ∠BDA = ∠CAB = ∠CAD = ∠DBC = ∠DBA = 45°
— äèàãîíàëè äåëÿò êâàäðàò íà 4 îäèíàêîâûõ òðåóãîëüíèêà, êðîìå òîãî, ïîëó÷åííûå òðåóãîëüíèêè â îäíî âðåìÿ è ðàâíîáåäðåííûå è ïðÿìîóãîëüíûå:
ΔAOB = ΔBOC = ΔCOD = ΔDOA
Äèàãîíàëü êâàäðàòà.
Äèàãîíàëüþ êâàäðàòà ÿâëÿåòñÿ âñÿêèé îòðåçîê, êîòîðûé ñîåäèíÿåò 2-å âåðøèíû ïðîòèâîëåæàùèõ óãëîâ êâàäðàòà.
Äèàãîíàëü âñÿêîãî êâàäðàòà áîëüøå ñòîðîíû ýòîãî êâàäðàòà â √2 ðàç.
Ôîðìóëû äëÿ îïðåäåëåíèÿ äëèíû äèàãîíàëè êâàäðàòà:
1. Ôîðìóëà äèàãîíàëè êâàäðàòà ÷åðåç ñòîðîíó êâàäðàòà:

2. Ôîðìóëà äèàãîíàëè êâàäðàòà ÷åðåç ïëîùàäü êâàäðàòà:

3. Ôîðìóëà äèàãîíàëè êâàäðàòà ÷åðåç ïåðèìåòð êâàäðàòà:

4. Ñóììà óãëîâ êâàäðàòà = 360°:

5. Äèàãîíàëè êâàäðàòà îäíîé äëèíû:

6. Âñå äèàãîíàëè êâàäðàòà äåëÿò êâàäðàò íà 2-å îäèíàêîâûå ôèãóðû, êîòîðûå ñèììåòðè÷íû:

7. Óãîë ïåðåñå÷åíèÿ äèàãîíàëåé êâàäðàòà ðàâåí 90°, ïåðåñåêàÿ äðóã äðóãà, äèàãîíàëè äåëÿòñÿ íà äâå ðàâíûå ÷àñòè:

8. Ôîðìóëà äèàãîíàëè êâàäðàòà ÷åðåç äëèíó îòðåçêà l:

9. Ôîðìóëà äèàãîíàëè êâàäðàòà ÷åðåç ðàäèóñ âïèñàííîé îêðóæíîñòè:

R — ðàäèóñ âïèñàííîé îêðóæíîñòè;
D — äèàìåòð âïèñàííîé îêðóæíîñòè;
d — äèàãîíàëü êâàäðàòà.

10. Ôîðìóëà äèàãîíàëè êâàäðàòà ÷åðåç ðàäèóñ îïèñàííîé îêðóæíîñòè:

R – ðàäèóñ îïèñàííîé îêðóæíîñòè;
D – äèàìåòð îïèñàííîé îêðóæíîñòè;
d – äèàãîíàëü.

11. Ôîðìóëà äèàãîíàëè êâàäðàòà ÷åðåç ëèíèþ, êîòîðàÿ âûõîäèò èç óãëà íà ñåðåäèíó ñòîðîíû êâàäðàòà:

C – ëèíèÿ, êîòîðàÿ âûõîäèò èç óãëà íà ñåðåäèíó ñòîðîíû êâàäðàòà;
d – äèàãîíàëü.

Ïåðèìåòð êâàäðàòà. Ïëîùàäü êâàäðàòà.
Âïèñàííûé êðóã â êâàäðàò – ýòî êðóã, ïðèìûêàþùèé ê ñåðåäèíàì ñòîðîí êâàäðàòà è èìåþùèé öåíòð íà ïåðåñå÷åíèè äèàãîíàëåé êâàäðàòà.
Ðàäèóñ âïèñàííîé îêðóæíîñòè — ñòîðîíà êâàäðàòà (ïîëîâèíà).
Ïëîùàäü êðóãà âïèñàííîãî â êâàäðàò ìåíüøå ïëîùàäè êâàäðàòà â π/4 ðàçà.
Êðóã, îïèñàííûé âîêðóã êâàäðàòà — ýòî êðóã, êîòîðûé ïðîõîäèò ÷åðåç 4-ðå âåðøèíû êâàäðàòà è êîòîðûé èìååò öåíòð íà ïåðåñå÷åíèè äèàãîíàëåé êâàäðàòà.
Ðàäèóñ îêðóæíîñòè îïèñàííîé âîêðóã êâàäðàòà áîëüøå ðàäèóñà âïèñàííîé îêðóæíîñòè â √2 ðàç.
Ðàäèóñ îêðóæíîñòè îïèñàííîé âîêðóã êâàäðàòà ðàâåí 1/2 äèàãîíàëè.
Ïëîùàäü êðóãà îïèñàííîãî âîêðóã êâàäðàòà áîëüøàÿ ïëîùàäü òîãî æå êâàäðàòà â π/2 ðàç.
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
СОДЕРЖАНИЕ СТАТЬИ
1. Параллелограмм
Сложное слово «параллелограмм»? А скрывается за ним очень простая фигура.
Смотри:
 | Параллелограмм – это четырехугольник, противоположные стороны которого попарно параллельны |
Ну, то есть, взяли две параллельные прямые:

Пересекли ещё двумя:

И вот внутри – параллелограмм!
Какие же есть свойства у параллелограмма?
Свойства параллелограмма.
То есть, чем можно пользоваться, если в задаче дан параллелограмм?
На этот вопрос отвечает следующая теорема:
В любом параллелограмме:
- Противоположные стороны равны
- Противоположные углы равны
- Диагонали делятся пополам точкой пересечения
Давай нарисуем все подробно.
Что означает первый пункт теоремы? А то, что если у тебя ЕСТЬ параллелограмм, то непременно
 | и . |
Второй пункт означает, что если ЕСТЬ параллелограмм, то, опять же, непременно:
 | и |
Ну, и наконец, третий пункт означает, что если у тебя ЕСТЬ параллелограмм, то обязательно:
 | и |
Видишь, какое богатство выбора? Что же использовать в задаче? Попробуй ориентироваться на вопрос задачи, или просто пробуй все по очереди – какой-нибудь «ключик» да подойдёт.
А теперь зададимся другим вопросом: а как узнать параллелограмм «в лицо»? Что такое должно случиться с четырехугольником, чтобы мы имели право выдать ему «звание» параллелограмма?
На этот вопрос отвечает несколько признаков параллелограмма.
Признаки параллелограмма.
Внимание! Начинаем.
- Признак 1. Если у четырехугольника две стороны равны и параллельны, то это – параллелограмм.
 | ; — параллелограмм. |
— паралелограмм.
- Признак 2. Если у четырехугольника противоположные стороны равны, то это – параллелограмм.
 | ; – параллелограмм. |
- Признак 3. Если у четырехугольника противоположные углы равны, то это – параллелограмм.
 | ; – параллелограмм. |
- Признак 4. Если у четырехугольника диагонали делятся точкой пересечения пополам, то это – параллелограмм.
 | ; – параллелограмм. |
Обрати внимание: если ты нашёл хотя бы один признак в своей задаче, то у тебя точно параллелограмм, и ты можешь пользоваться всеми свойствами параллелограмма.
Для полной ясности посмотри на схему:

2. Прямоугольник
Думаю, что для тебя вовсе не явится новостью то, что
 | Прямоугольник – четырехугольник, все углы которого прямые. |
Первый вопрос: а является ли прямоугольник параллелограммом?
Конечно, является! Ведь у него и — помнишь, наш признак 3?
А отсюда, конечно же, следует, что у прямоугольника, как и у всякого параллелограмма и , а диагонали точкой пересечения делятся пополам.
Но есть у прямоугольника и одно отличительноесвойство.
Свойство прямоугольника
 | Диагонали прямоугольника равны: . |
Почему это свойство отличительное? Потому что ни у какого другого параллелограмма не бывает равных диагоналей. Сформулируем более чётко.
 | Если у параллелограмма равны диагонали, то это — прямоугольник. |
Обрати внимание: чтобы стать прямоугольником, четырехугольнику нужно сперва стать параллелограммом, а потом уже предъявлять равенство диагоналей.
3. Ромб
 | Ромб – четырехугольник, все стороны которого равны между собой. |
И снова вопрос: ромб – это параллелограмм или нет?
С полным правом – параллелограмм, потому что у него и (вспоминаем наш признак 2).
И снова, раз ромб – параллелограмм, то он обязан обладать всеми свойствами параллелограмма. Это означает, что у ромба противоположные углы равны, противоположные стороны параллельны, а диагонали делятся точкой пересечения пополам.
Но есть и особенные свойства. Формулируем.
Свойства ромба
- Свойство 1. Диагонали ромба перпендикулярны.
 | (если ты забыл, напомню: — значок перпендикулярности) |
- Свойство 2. Диагонали ромба являются биссектрисами его углов.
Посмотри на картинку:

Как и в случае с прямоугольником, свойства эти – отличительные, то есть по каждому из этих свойств можно заключить, что перед нами не просто параллелограмм, а именно ромб.
Признаки ромба
- Признак 1. Если в параллелограмме диагонали перпендикулярны, то это ромб.

- Признак 2. Если в параллелограммехотя бы одна из диагоналей делит пополам оба угла, через которые она проходит, то этот параллелограмм – ромб.

И снова обрати внимание: должен быть не просто четырехугольник, у которого перпендикулярны диагонали, а именно параллелограмм. Убедись:
 | разве это ромб? |
Нет, конечно, хотя его диагонали и перпендикулярны, а диагональ – биссектриса углов и . Но … диагонали не делятся, точкой пересечения пополам, поэтому – НЕ параллелограмм, а значит, и НЕ ромб.
4. Квадрат
 | Квадрат – четырехугольник, у которого все стороны равны между собой, а все углы – прямые. |
То есть квадрат – это прямоугольник и ромб одновременно. Давай посмотрим, что из этого получится.
 | У квадрата угол между диагональю и стороной равен . |
Понятно почему? Квадрат — ромб – биссектриса угла A, который равен . Значит делит (да и тоже) на два угла по .
 | Диагонали квадрата равны, перпендикулярны и делятся точкой пересечения пополам. |
Ну, это совсем ясно: прямоугольник диагонали равны; ромб диагонали перпендикулярны, и вообще – параллелограмм диагонали делятся точкой пересечения пополам.
 | Если сторона квадрата равна , то его диагональ равна . |
Почему? Ну, просто применим теорему Пифагора к .
Значит, .
СРЕДНИЙ УРОВЕНЬ
Свойства четырехугольников. Параллелограмм
Параллелограмм – это четырехугольник, противоположные стороны которого попарно параллельны.

Свойства параллелограмма
Внимание! Слова «свойства параллелограмма» означают, что если у тебя в задаче есть параллелограмм, то всем нижеследующим можно пользоваться.
Итак,
Теорема о свойствах параллелограмма.
В любом параллелограмме:
Давай-ка поймём, почему это всё верно, иными словами ДОКАЖЕМ теорему.
Итак, почему верно 1)?
 | Давай проведём диагональ . Что получится? Два треугольника: и . |
Раз – параллелограмм, то :
- как накрест лежащие
- как накрест лежащие.
Значит, (по II признаку: и — общая.)
Ну вот, а раз , то и – всё! – доказали.
Но кстати! Мы ещё доказали при этом и 2)!
Почему? Но ведь (смотри на картинку), то есть , а именно потому, что .
Осталось только 3).
Для этого всё-таки придётся провести вторую диагональ.
 | Мы уже выяснили, что . Давай снова отметим равные накрест лежащие углы (посмотри и убедись, что все верно). |
И теперь видим, что — по II признаку ( угла и сторона «между» ними).
 | Значит, (напротив углов и ) и (напротив углов и соответственно). |
Свойства доказали! Перейдём к признакам.
Признаки параллелограмма
Напомним, что признак параллелограмма отвечает на вопрос «как узнать?», что фигура является параллелограммом.
Признак 1. Если у четырехугольника две стороны равны и параллельны, то это параллелограмм.
В значках это так:
 | ; – параллелограмм. |
Почему? Хорошо бы понять, почему – этого хватит. Но смотри:
 | по 1 признаку: , — общая и как накрест лежащие при параллельных и и секущей . |
А раз ,
 | то (лежат напротив и соответственно). Но это значит, что ( и — накрест лежащие и оказались равны). |
Ну вот и разобрались, почему признак 1 верен.
Признак 2. Если у четырехугольника противоположные стороны равны, то это – параллелограмм.
 | , – параллелограмм. |
Ну, это ещё легче! Снова проведём диагональ .
 | Теперь просто по трём сторонам. |
А значит:
 | и , то есть – параллелограмм. |
Признак 3. Если у четырёхугольника противоположные углы равны, то это – параллелограмм.
 | , – параллелограмм. |
И тоже несложно. Но …по-другому!
 | (ведь – четырехугольник, а , по условию). |
Значит, . Ух! Но и – внутренние односторонние при секущей !
Поэтому тот факт, что означает, что .
А если посмотришь с другой стороны, то и – внутренние односторонние при секущей ! И поэтому .
Видишь, как здорово?!
Признак 4. Если у четырехугольника диагонали делятся точкой пересечения пополам, то это – параллелограмм.
 | ; – параллелограмм. |
И опять просто:
 | , как вертикальные , , и . |
Точно так же , , и .
Обрати внимание: если ты нашел хотя бы один признак параллелограмма в своей задаче, то у тебя точно параллелограмм, и ты можешь пользоваться всеми свойствами параллелограмм