Какое явление или свойство тел характеризует сила упругости

Сила упругости
Любое тело, когда его деформируют и оказывают внешнее воздействие, сопротивляется и стремиться восстановить прежние форму и размеры. Это происходит по причине электромагнитного взаимодействия в теле на молекулярном уровне.
Деформация — изменение положения частиц тела друг относительно друга. Результат деформации — изменение межатомных расстояний и перегруппировка блоков атомов.
Определение. Что такое сила упругости?
Сила упругости — сила, возникающая при деформации в теле и стремящаяся вернуть тело в начальное состояние.
Рассмотрим простейшие деформации — растяжение и сжатие
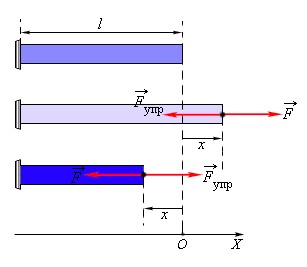
На рисунке показано, как действует сила упругости, когда мы сжимаем или растягиваем стержень.
Закон Гука
Для малых деформаций x≪ l справедлив закон Гука.
Закон Гука
Деформация, возникающая в упругом теле, пропорциональна приложенной к телу силе.
Fупр=-kx
Здесь k — коэффициент пропорциональности, называемый жесткостью. Единица измерения жесткости системе СИ Ньютон на метр. Жесткость зависит от материала тела, его формы и размеров.
Знак минус показывает, что сила упругости противодействует внешней силе и стремится вернуть тело в первоначальное состояние.
Существуют и другие формы записи закона Гука. Относительной деформацией тела называется отношение ε=xl. Напряжением в теле называется отношение σ=-FупрS. Здесь S — площадь поперечного сечения деформированного тела. Вторая формулировка закона Гука: относительная деформация пропорциональна напряжению.
ε=σE.
Здесь E — так называемый модуль Юнга, который не зависит от формы и размеров тела, а зависит только от свойств материала. Значение модуля Юнга для различных материалов широко варьируется. Например, для стали E≈2·1011 Нм2, а для резины E≈2·106 Нм2
Закон Гука можно обобщить для случая сложных деформаций. Рассмотрим деформацию изгиба стержня. При такой деформации изгиба сила упругости пропорциональна прогибу стержня.
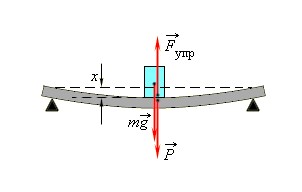
Концы стержня лежат на двух опорах, которые действуют на тело с силой N→, называемой силой нормальной реакции опоры. Почему нормальной? Потому что эта сила направлена перпендикулярно (нормально) поверхности соприкосновения.
Если стержень лежит на столе, сила нормальной реакции опоры направлена вертикально вверх, противоположно силе тяжести, которую она уравновешивает.
Вес тела — это сила, с которой оно действует на опору.
Силу упругости часто рассматривают в контексте растяжения или сжатия пружины. Это распространенный пример, который часто встречается не только в теории, но и на практике. Пружины используются для измерения величины сил. Прибор, предназначенный для этого — динамаметр.
Динамометр — пружина, растяжение которой проградуированно в единицах силы. Характерное свойство пружин заключается в том, что закон Гука для них применим при достаточно большом изменении длины.
При сжатии и растяжении пружины действует закон Гука, возникают упругие силы, пропорциональные изменению длины пружины и ее жесткости (коэффициента k).
В отличие от пружин стержни и проволоки подчиняются закону Гука в очень узких пределах. Так, при относительной дефомации больше 1% в материале возникают необратимые именения — текучесть и разрушения.
Под действием приложенных внешних сил твердые тела изменяют свою форму и объем — деформируются. Если после прекращения действия силы, форма и объем тела полностью восстанавливаются, то деформацию называют упругой, а тело — абсолютно упругим. Деформации, которые не исчезают после прекращения действия сил, называются пластическими, а тела — пластичными.
Различают следующие виды деформаций: растяжение, сжатие, сдвиг, кручение и изгиб.
Деформацию растяжения характеризуют абсолютным удлинением дельта l и относительным удлинением е:
где l0— начальная длина, l— конечная длина стержня. Механическим напряжением называют отношение модуля силы упругости F к площади поперечного сечения тела S:б=F/S.
В СИ за единицу механического напряжения принимают 1Па = 1Н/м2.
Закон Гука (1635-1703): при малых деформациях напряжение прямо пропорционально относительному удлинению (б = Е • е). На рис.33 представлен график зависимости механического напряжения от относительного удлинения.
Участок 0А — область пропорциональности: на этом участке выполняется закон Гука. Точке А соответствует напряжение бпроп, называемое пределом пропорциональности.
Предел пропорциональности бпроп — максимальное напряжение, при котором закон Гука еще выполняется.
Предел упругости бупр — напряжение, при котором тело полностью утрачивает упругость (участок АВ).
На участке ВС наблюдается явление «текучести» материала: удлинение тела нарастает при незначительном росте деформирующей силы.
При дальнейшем увеличении удлинения тело вновь обретает способность сопротивляться деформации; напряжение в нем вновь увеличивается, достигая максимума в точке D, которой соответствует начало разрушения.
Предел прочности бпроч — наибольшее напряжение, возникающее в теле перед началом разрушения. Участку DE соответствует постепенное разрушение тела.
Все детали машин и механизмов изготавливаются со значительным, но разумным запасом прочности.
Отношение предела прочности материала (или предела текучести для пластичных тел) к фактически действующему напряжению называют коэффициентом запаса прочности (k). Например, в строительном деле коэффициент запаса прочности стальных балокустановлен не менее 2,5 — 2,6, а для балок из хрупких материалов (чугун, бетон) не менее 3 — 9.
Механические свойства материалов различны. Такие материалы, как резина или сталь, обнаруживают упругие свойства при сравнительно больших напряжениях и деформациях. Их называют упругими.
Материалы, у которых незначительные нагрузки вызывают пластические деформации, называют пластичными (пластилин, свинец).
Большое значение на практике имеет такое свойство твердых тел, как хрупкость. Материалы называют хрупкими, если они разрушаются при небольших деформациях (чугун, фарфор).
Важной характеристикой материалов является твердость. Она характеризует способность материала оказывать сопротивление проникновению в него другого тела, т. е. способность противодействовать вдавливанию или царапанью.)
Деформация и напряжение. Деформацию сжатия и растяжения можно характеризовать абсолютным удлинением Δl, равным разности длин образца до растяжения l0 и после него l :
.
Абсолютное удлинение при растяжении положительно, при сжатии имеет отрицательное значение.
Отношение абсолютного удлинения к длине образца называется относительным удлинением :
. (30.1)
При деформации тела возникают силы упругости. Физическая величина, равная отношению модуля силы упругости к площади сечения тела, называется механическим напряжением :
. (30.2)
За единицу механического напряжения в СИ принят паскалъ (Па). .
Модуль упругости. При малых деформациях напряжение прямо пропорционально относительному удлинению:
. (30.3)
Коэффициент пропорциональности Е в уравнении (30.3) называется модулем упругости. Модуль упругости одинаков для образцов любой формы и размеров, изготовленных из одного материала:
. (30.4)
Из формулы (30.4) следует, что
. (30.5)
Сравнив выражение (30.5) с законом Гука, получим, что жесткость k стержня пропорциональна произведению модуля Юнга на площадь поперечного сечения стержня и обратно пропорциональна его длине.
Диаграмма растяжения. Зависимость напряжения от относительного удлинения является одной из важнейших характеристик механических свойств твердых тел. Графическое изображение этой зависимости называется диаграммой растяжения. По оси ординат откладывается механическое напряжение , по оси абсцисс — относительное удлинение (рис. 102).
Закон Гука выполняется при небольших деформациях. Максимальное напряжение , при котором еще выполняется закон Гука, называется пределом пропорциональности. За пределом пропорциональности (точка А) напряжение перестает быть пропорциональным относительному удлинению; до некоторого напряжения после снятия нагрузки размеры тела восстанавливаются полностью. Такая деформация называется упругой.Максимальное напряжение , при котором деформация еще остается упругой, называется пределом упругости(точка В). Большинство металлов испытывает упругую деформацию до значений .
При напряжениях, превышающих предел упругости , образец после снятия нагрузки не восстанавливает свою форму или первоначальные размеры. Такие деформации называются остаточными или пластическими.
В области пластической деформации (участок CD) деформация происходит почти без увеличения напряжения. Это явление называется текучестью материала.
Материалы, у котерых область текучести CD значительна, могут без разрушения выдерживать большие деформации. Если же область текучести материала почти отсутствует, он без разрушения сможет выдержать лишь небольшие деформации. Такие материалы называются хрупкими. Примерами хрупких материалов могут служить стекло, кирпич, бетон, чугун.
За пределом текучести кривая напряжений поднимается и достигает максимума в точке Е. Напряжение, соответствующее точке Е, называется пределом прочности . После точки Е кривая идет вниз и дальнейшая деформация вплоть до разрыва (точка К) происходит при все меньшем напряжении.
Дефекты в кристаллах. Способы повышения прочности твердых тел. Кристаллическими телами являются все металлические изделия — стальные каркасы зданий и мостов, рельсы железных дорог, линии электропередач, станки, машины, поезда, самолеты.
Одной из важнейших задач науки и техники является создание прочных и надежных машин, станков и зданий с минимальной затратой металлов и других материалов.
Сравнение реальной прочности кристаллов со значениями, полученными на основании теоретических расчетов, обнаруживает весьма существенные расхождения. Теоретический предел прочности в десятки и даже в сотни раз превосходит значения, получаемые при испытаниях реальных образцов.
Оказалось, что причина расхождения теории и эксперимента заключается в наличии внутренних и поверхностных дефектов в строении кристаллических решеток.
Самые простые дефекты в идеальной кристаллической решетке — точечные дефекты — возникают при замещении собственного атома чужеродным, внедрении атома в пространство между узлами решетки или при отсутствии атома в одном из узлов кристаллической решетки (рис. 103).
Другой вид дефектов — линейные дефекты — возникает при нарушениях в порядке расположения атомных плоскостей в кристаллах. Пример такого нарушения в структуре кристалла представлен на рисунке 104.
Деформация и разрушение кристалла с линейным дефектом облегчаются потому, что вместо одновременного разрыва всех связей между атомами двух плоскостей становится возможным поочередный разрыв небольшого числа связей между атомами с постепенным перемещением дефекта в кристалле.
Для получения кристаллических материалов с высокой прочностью нужно выращивать монокристаллы без дефектов. Это очень сложная задача, и поэтому в практике этот путь пока широкого распространения не получил.
Большинство современных методов упрочнения материалов основано на другом способе. Для упрочнения кристалла с дефектами в решетке можно создать условия, при которых перемещение дефектов в кристалле затрудняется. Препятствием для перемещения дефектов в кристалле могут служить другие дефекты, специально созданные в кристаллической решетке. Так, для увеличения прочности стали применяется легирование стали — введение в расплав небольших добавок хрома, вольфрама и других элементов. Внедрение атомов чужеродных элементов в решетку кристаллов железа затрудняет перемещение линейных дефектов при деформации кристаллов, прочность стали повышается при этом примерно в три раза. Дополнительные дефекты в кристаллической решетке создаются при протяжке, дробеструйной обработке металлов. Эти виды обработки могут повышать прочность материалов примерно в два раза.
Упругость — свойство восстанавливать форму тела после прекращения воздействия других тел или полей.
Деформация — изменение формы и размеров твердых тел под действием внешних сил. Деформации могут быть упругими и пластичными.
Упругая деформация — деформация, при которой после прекращения действия внешних сил тело восстанавливает прежние размеры и форму.
Пластическая (остаточная) деформация — деформация, которая не исчезает в теле после прекращения действия внешних сил.
Все виды возможных деформаций (растяжение или сжатие, сдвиг, изгиб, кручение) могут быть сведены к двум одновременно происходящим деформациям — растяжению (или сжатию) и сдвигу.
Относительная деформация — мера деформации, равная отношению абсолютной деформации Ах к первоначальному значению величины х, характеризующей размеры и форму тела.
Если к концам стержня (рис. 3.14) с площадью поперечного сечения S приложены направленные вдоль его оси внешние силы Fj и Р2 (Fj = F2 = F), то длина стержня I получит положительное (при растягивании) или отрицательное (при сжатии) приращение Al, принятое называть абсолютным удлинением. Изменение длины стержня сопровождается изменением диаметра d стержня, причем при растяжении Al > О, Ad 0, при сжатии — Al 0.

Рис. 3.14
Относительное удлинение (сжатие) — это отношение абсолютного удлинения А? к начальной длине I тела:

Сила упругости Fynp — сила, возникающая при деформации тела и направленная в сторону, противоположную перемещению частиц при деформации.
Напряжение а — физическая величина, равная по модулю силе упругости, действующей на единицу площади поперечного сечения тела:

Закон Гука: в пределах упругой деформации напряжение прямо пропорционально относительной деформации:

где Е — модуль Юнга (модуль Юнга равен напряжению, когда относительное удлинение равно единице, т. е. при е = 1 получаем ст = Е).
Закон Гука справедлив только для упругих деформаций, исчезающих после прекращения действия сил.
Закон Гука можно представить в виде:

Сопоставив данное выражение с формулой закона Гука F = = -кх, где к — жесткость тела, получим:

В зависимости от условий внешнего воздействия различают несколько видов деформации. В теории упругости доказывается, что все виды деформаций (растяжение или сжатие, сдвиг, изгиб, кручение) могут быть сведены к одновременно происходящим деформациям растяжения или сжатия и сдвига.
Деформация (растяжения) сжатия возникает (рис. 3.15, а), если к концам стержня длиной I и площадью поперечного сечения S прикладываются направленные вдоль его оси силы F] и F2 (Fj = F2 = F), в результате чего длина стержня меняется на величину Д/.
Деформацию сдвига проще всего осуществить, если взять брусок и приложить к нему силу F (рис. 3.15,6), касательную к его поверхности (нижняя часть бруска закреплена неподвижно). Относительная деформация сдвига определяется из формулы:

где Д/ — абсолютный сдвиг параллельных слоев тела относительно друг друга; у — расстояние между слоями (при малых углах имеет место tgy ~ у).
Деформация изгиба характеризуется искривлением оси или срединной поверхности деформируемого тела (балка, стержень) под действием внешних сил (рис. 3.15, в).
Если на середину прямого упругого стержня, свободно наложенного на твердые опорные призмы, действует сила F (рис. 3.15, в), то стержень изгибается. При таком изгибе верхние слои сжимаются, нижние — растягиваются, а некоторый

Рис. 3.15
средний слой, который называют нейтральным, сохраняет длину и только претерпевает искривление.
Деформация кручения характеризуется взаимным поворотом поперечных сечений стержня под влиянием пар сил, действующих в плоскости этих сечений (рис. 3.15, г).
Предел прочности материала стпред — предельное напряжение, при котором тело начинает разрушаться.
Запас прочности — скалярная величина, равная отношению предельного напряжения апред к допустимому стдоп:

Связь между напряжением ст и деформацией в представляют в виде диаграмм напряжений (рис. 3.16).

Рис. 3.1 б
Тестирование онлайн
Что надо знать о силе
Сила — векторная величина. Необходимо знать точку приложения и направление каждой силы. Важно уметь определить какие именно силы действуют на тело и в каком направлении. Сила обозначается как , измеряется в Ньютонах. Для того, чтобы различать силы, их обозначают следующим образом
Ниже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя!
Сил в природе много. Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах.
Сила тяжести
На каждое тело, находящееся на планете, действует гравитация Земли. Сила, с которой Земля притягивает каждое тело, определяется по формуле

Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз.
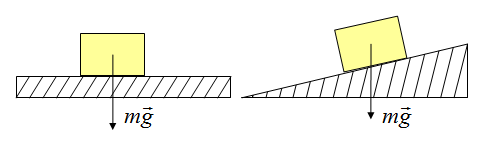
Сила трения
Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей. Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:

Сила приложена в точке соприкосновения двух поверхностей. Направлена в сторону противоположную движению.
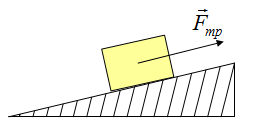
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила реакции опоры
Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы «говорит» реагирует опора. Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, «сопротивляются».
Абсолютно любое тело, даже очень легкое (например,карандаш, лежащий на столе), на микроуровне деформирует опору. Поэтому возникает реакция опоры.
Специальной формулы для нахождения этой силы нет. Обозначают ее буквой , но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как
Сила приложена в точке соприкосновения предмета с опорой. Направлена перпендикулярно опоре.
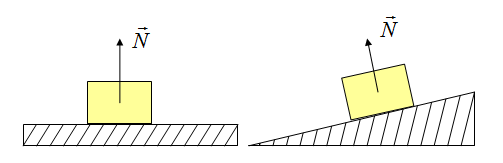
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила упругости
Это сила возникает в результате деформации (изменения первоначального состояния вещества). Например, когда растягиваем пружину, мы увеличиваем расстояние между молекулами материала пружины. Когда сжимаем пружину — уменьшаем. Когда перекручиваем или сдвигаем. Во всех этих примерах возникает сила, которая препятствует деформации — сила упругости.
Закон Гука

Сила упругости направлена противоположно деформации.

Так как тело представляем в виде материальной точки, силу можно изображать с центра
При последовательном соединении, например, пружин жесткость рассчитывается по формуле

При параллельном соединении жесткость

Жесткость образца. Модуль Юнга.

Модуль Юнга характеризует упругие свойства вещества. Это постоянная величина, зависящая только от материала, его физического состояния. Характеризует способность материала сопротивляться деформации растяжения или сжатия. Значение модуля Юнга табличное.
Подробнее о свойствах твердых тел здесь.
Вес тела
Вес тела — это сила, с которой предмет воздействует на опору. Вы скажете, так это же сила тяжести! Путаница происходит в следующем: действительно часто вес тела равен силе тяжести, но это силы совершенно разные. Сила тяжести — сила, которая возникает в результате взаимодействия с Землей. Вес — результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же — сила, которая приложена на опору (не на предмет)!
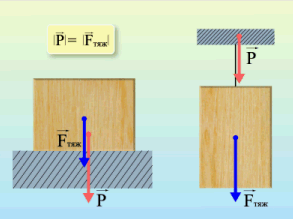
Формулы определения веса нет. Обозначается эта силы буквой .
Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление.

Сила реакции опоры и вес — силы одной природы, согласно 3 закону Ньютона они равны и противоположно направлены. Вес — это сила, которая действует на опору, а не на тело. Сила тяжести действует на тело.
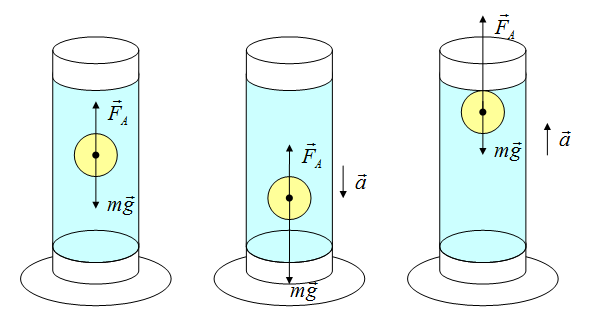
Вес тела может быть не равен силе тяжести. Может быть как больше, так и меньше, а может быть и такое, что вес равен нулю. Это состояние называется невесомостью. Невесомость — состояние, когда предмет не взаимодействует с опорой, например, состояние полета: сила тяжести есть, а вес равен нулю!

Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила
Обратите внимание, вес — сила, измеряется в Ньютонах. Как верно ответить на вопрос: «Сколько ты весишь»? Мы отвечаем 50 кг, называя не вес, а свою массу! В этом примере, наш вес равен силе тяжести, то есть примерно 500Н!
Перегрузка — отношение веса к силе тяжести
Сила Архимеда
Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:
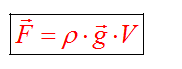
В воздухе силой Архимеда пренебрегаем.
Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше — тонет.
Электрические силы
Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как сила Кулона, сила Ампера, сила Лоренца, подробно рассмотрены в разделе Электричество.
Схематичное обозначение действующих на тело сил
Часто тело моделируют материальной точкой. Поэтому на схемах различные точки приложения переносят в одну точку — в центр, а тело изображают схематично кругом или прямоугольником.
Для того, чтобы верно обозначить силы, необходимо перечислить все тела, с которыми исследуемое тело взаимодействует. Определить, что происходит в результате взаимодействия с каждым: трение, деформация, притяжение или может быть отталкивание. Определить вид силы, верно обозначить направление. Внимание! Количество сил будет совпадать с числом тел, с которыми происходит взаимодействие.
Главное запомнить
1) Силы и их природа;
2) Направление сил;
3) Уметь обозначить действующие силы
