Какое из перечисленных свойств относится к функции y x sinx
Теория
| 1. | Свойства функции y = sinx и её график |
Задания
| 1. | Возрастание и убывание функции y = sinx Сложность: | 1 |
| 2. | Определение значений синусов некоторых углов Сложность: | 1 |
| 3. | Преобразование выражения sin t и определение его значения Сложность: | 1 |
| 4. | Сравнение чисел с использованием свойств функции y = sinx Сложность: | 1 |
| 5. | Принадлежность точек графику Сложность: | 1 |
| 6. | Построение графика функции y = sin x Сложность: | 1 |
| 7. | Нахождение наибольшего и наименьшего значений функции y = sinx Сложность: | 1 |
| 8. | Область значений функции y = sinx Сложность: | 1 |
| 9. | Определение чётности функции Сложность: | 1 |
| 10. | Решение уравнения графически Сложность: | 1 |
| 11. | Определение наибольшего и наименьшего значений функции Сложность: | 2 |
| 12. | Построение графиков функций y = sin(x + a) + b Сложность: | 4 |
Тесты
| 1. | Тренировка по теме Функция y = sinx Сложность: лёгкое | 3 |
Методические материалы
| 1. | Технологическая карта |
Функции y = sinx, y = cosx, y = mf(x), y = f(kx), y = tgx, y = ctgx
Функция y = sin x
Графиком функции является синусоида.
Полную неповторяющуюся часть синусоиды называют волной синусоиды.
Половину волны синусоиды называют полуволной синусоиды (или аркой).
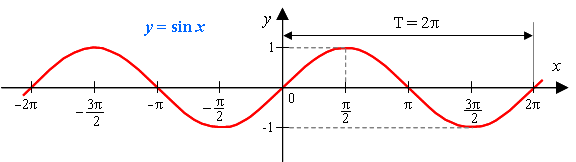
Свойства функции y = sin x:
1) Область определения функции – множество действительных чисел.
2) Область значений функции – отрезок [–1; 1]
3) Это нечетная функция.
4) Это непрерывная функция.
5) Координаты точек пересечения графика:
— с осью абсцисс: (πn; 0),
— с осью ординат: (0; 0).
6) На отрезке [-π/2; π/2] функция возрастает, на отрезке [π/2; 3π/2] – убывает.
7) На промежутках [2πn; π + 2πn] функция принимает положительные значения.
На промежутках [-π + 2πn; 2πn] функция принимает отрицательные значения.
8) Промежутки возрастания функции: [-π/2 + 2πn; π/2 + 2πn].
Промежутки убывания функции: [π/2 + 2πn; 3π/2 + 2πn].
9) Точки минимума функции: -π/2 + 2πn.
Точки максимума функции: π/2 + 2πn
10) Функция ограничена сверху и снизу. Наименьшее значение функции –1,
наибольшее значение 1.
11) Это периодическая функция с периодом 2π (Т = 2π)
Для построения графика функции y = sin x удобно применять следующие масштабы:
— на листе в клетку за единицу отрезка примем длину в две клетки.
— на оси x отмерим длину π. При этом для удобства 3,14 представим в виде 3 – то есть без дроби. Тогда на листе в клетку π составит 6 клеток (трижды по 2 клетки). А каждая клетка получит свое закономерное имя (от первой до шестой): π/6, π/3, π/2, 2π/3, 5π/6, π. Это значения x.
— на оси y отметим 1, включающий две клетки.
Составим таблицу значений функции, применяя наши значения x:
| π | π | π | 2π | 5π | |
| 1 | √3 | | √3 | 1 |
Далее составим график. Получится полуволна, наивысшая точка которой (π/2; 1). Это график функции y = sin x на отрезке [0; π]. Добавим к построенному графику симметричную полуволну (симметричную относительно начала координат, то есть на отрезке -π). Гребень этой полуволны – под осью x с координатами (-1; -1). В результате получится волна. Это график функции y = sin x на отрезке [-π; π].
Можно продолжить волну, построив ее и на отрезке [π; 3π], [π; 5π], [π; 7π] и т.д. На всех этих отрезках график функции будет выглядеть так же, как на отрезке [-π; π]. Получится непрерывная волнистая линия с одинаковыми волнами.
Функция y = cos x.
Графиком функции является синусоида (ее иногда называют косинусоидой).
Свойства функции y = cos x:
1) Область определения функции – множество действительных чисел.
2) Область значений функции – отрезок [–1; 1]
3) Это четная функция.
4) Это непрерывная функция.
5) Координаты точек пересечения графика:
— с осью абсцисс: (π/2 + πn; 0),
— с осью ординат: (0;1).
6) На отрезке [0; π] функция убывает, на отрезке [π; 2π] – возрастает.
7) На промежутках [-π/2 + 2πn; π/2 + 2πn] функция принимает положительные значения.
На промежутках [π/2 + 2πn; 3π/2 + 2πn] функция принимает отрицательные значения.
8) Промежутки возрастания: [-π + 2πn; 2πn].
Промежутки убывания: [2πn; π + 2πn];
9) Точки минимума функции: π + 2πn.
Точки максимума функции: 2πn.
10) Функция ограничена сверху и снизу. Наименьшее значение функции –1,
наибольшее значение 1.
11) Это периодическая функция с периодом 2π (Т = 2π)
Функция y = mf(x).
Возьмем предыдущую функцию y = cos x. Как вы уже знаете, ее графиком является синусоида. Если мы умножим косинус этой функции на определенное число m, то волна растянется от оси x (либо сожмется, в зависимости от величины m).
Эта новая волна и будет графиком функции y = mf(x), где m – любое действительное число.
Таким образом, функция y = mf(x) – это привычная нам функция y = f(x), умноженная на m.
Если m < 1, то синусоида сжимается к оси x на коэффициент m. Если m > 1, то синусоида растягивается от оси x на коэффициент m.
Выполняя растяжение или сжатие, можно сначала построить лишь одну полуволну синусоиды, а затем уже достроить весь график.
Функция y = f(kx).
Если функция y = mf(x) приводит к растяжению синусоиды от оси x либо сжатию к оси x, то функция y = f(kx) приводит к растяжению от оси y либо сжатию к оси y.
Причем k – любое действительное число.
При 0 < k < 1 синусоида растягивается от оси y на коэффициент k. Если k > 1, то синусоида сжимается к оси y на коэффициент k.
Составляя график этой функции, можно сначала построить одну полуволну синусоиды, а по ней достроить затем весь график.
Функция y = tg x.
Графиком функции y = tg x является тангенсоида.
Достаточно построить часть графика на промежутке от 0 до π/2, а затем можно симметрично продолжить ее на промежутке от 0 до 3π/2.
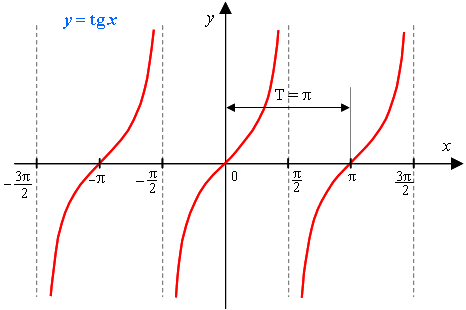
Свойства функции y = tg x:
1) Область определения функции – множество всех действительных чисел, кроме чисел вида
x = π/2 + πk, где k – любое целое число.
Это означает, что на графике функции нет точки, принадлежащей прямой x = π/2,
либо прямой x = 3π/2, либо прямой x = 5π/2, либо прямой x = –π/2 и т.д.
2) Область значений функции (–∞; +∞)
3) Это нечетная функция.
4) Это непрерывная функция на интервале (–π/2; π/2).
5) Это периодическая функция с основным периодом π (Т = π)
6) Функция возрастает на интервале (–π/2; π/2).
7) Функция не ограничена ни сверху, ни снизу. Не имеет ни наименьшего, ни наибольшего значений.
Функция y = ctg x
Графиком функции y = ctg x также является тангенсоида (ее иногда называют котангенсоидой).
Свойства функции y = ctg x:
1) Область определения функции – множество всех действительных чисел, кроме чисел вида
x = πk, где k – любое целое число.
2) Область значений функции (–∞; +∞)
3) Это нечетная функция.
4) Это непрерывная функция.
5) Это периодическая функция с основным периодом π (Т = π)
6) Функция убывает в промежутке (πk; π + πk), где k – любое целое число.
7) Функция не ограничена ни сверху, ни снизу. Не имеет ни наименьшего, ни наибольшего значений.
В этом параграфе обсудим некоторые свойства функций у = sin x,y = cos х и построим их графики.
1. Функция у = sin х.
Ранее мы сформулировали правило, позволяющее каждому числу t поставить в соответствие число sin t, т.е. охарактеризовали функцию u = sin t. Отметим некоторые ее свойства.
Свойства функции u = sin t.
Свойство 1: Область определения — множество R действительных чисел.
Это следует из того, что любому числу t соответствует на числовой окружности точка M(t), которая имеет вполне определенную ординату; эта ордината и есть sin t.
Свойство 2. u = sin t — нечетная функция.
Это следует из того, что для любого t выполняется равенство sin (-t) = -sin t.
Значит, график функции u = sin t, как график любой нечетной функции, симметричен относительно начала координат в прямоугольной системе координат tOu.
Свойство 3. Функция u = sin t возрастает на отрезке и убывает на отрезке .
Это следует из того, что при движении точки по первой четверти числовой окружности (от 0 до ) ордината постепенно увеличивается (от 0 до 1 — рис. 15), а при движении точки по второй четверти числовой окружности (от до ) ордината постепенно уменьшается (от 1 до 0 — рис. 16).
рис 15 рис 16
Свойство 4. Функция u = sin t ограничена и снизу, и сверху.
Это следует из того, что для любого t справедливо неравенство -1? sin t ? 1.
Свойство 5. uнаим = -1 (этого значения функция достигает в любой точке вида
); uнаиб = 1 (этого значения функция достигает в любой точке вида
).
Воспользовавшись полученными свойствами, построим график интересующей нас функции. Но вместо u = sin t будем писать у = sin х. Значит, и строить график будем в привычной системе координат хОу.
Сначала построим график функции у = sin x на отрезке [0, р].
Составим таблицу значений функции у = sin x:
Построим эти точки на координатной плоскости и соединим их плавной кривой. (рис 17)
Это — график функции у = sin x на отрезке [0, р]. Добавив к построенной линии симметричную ей относительно начала координат, получим график функции на отрезке [-р, р] А теперь построим график функции у = sin x на отрезке [р, Зр]. Обратите внимание: если х [-р, р], то (х + 2 р) [л, Зр]. Но sin(x + 2р) = sin х (по свойству 2). Это значит, что в точке х + 2р функция у = sin x принимает то же значение, что и в точке х.
рис 17
Иными словами, на отрезке [р, Зр] график функции выглядит точно так же, как и на отрезке [-р, р] (рис. 18).
рис 18
И на отрезках [Зр, 5р], [5р, 7р], [-Зр, -р] и т.д. график функции выглядит так же, как на отрезке [-р, р].
Окончательный вид графика функции у = sin x представлен на рис. 19.
рис 19
Линию, служащую графиком функции у = sin x, называют синусоидой. Ту часть синусоиды, которая изображена на рис. 18, называют волной синусоиды, а ту часть синусоиды, которая изображена на рис. 17, называют полуволной или аркой синусоиды. Опираясь на построенный график, отметим еще несколько свойств функции у = sin x:
Свойство 6. у = sin х — непрерывная функция.
Свойство 7. Область значений функции у = sin x — отрезок [-1, 1].
Свойство 8. Функция у — sin x выпукла вверх на отрезке [0, р], выпукла вниз на отрезке [р, 2р] и т.д.
2. Функция у = cos x.
Изучение функции у = cos x можно было бы провести примерно по той же схеме, которая была использована выше для функции у = sin х. Но мы выберем путь, быстрее приводящий к цели. Сначала докажем две формулы, важные сами по себе, но пока имеющие для наших целей лишь вспомогательное значение.
Для любого значения t справедливы равенства:
Построим график функции у = . Для этого перейдем к вспомогательной системе координат с началом в точке (пунктирная прямая х = проведена на рис. 20). Привяжем функцию у = sin x к новой системе координат — это и будет график функции у = (рис. 20), т.е. график функции у = cos х. Его, как и график функции у = sin x, называют синусоидой (что вполне естественно).
рис 20
Свойство 1. D(f) = (-?, + ?).
Свойство 2. у = cos х — четная функция.
Свойство 3. Функция убывает на отрезке [0, р], возрастает на отрезке [р, 2р] и т.д.
Свойство 4. Функция ограничена и снизу и сверху.
Свойство 5. унаим = -1 (этого значения функция достигает в любой точке вида ; унаиб = 1 (этого значения функция достигает в любой точке вида х = ).
Свойство 6. у = cos х — непрерывная функция.
Свойство 7. Е(y) = [-1. 1].
Свойство 8. Функция выпукла вверх на отрезке , выпукла вниз на отрезке и т.д.
Определение. Функцию у = f(х), хХ, называют периодической, если существует такое отличное от нуля число T, что для любого х из множества X выполняется двойное равенство:
f(x-T)=f(x)=f(x + T).
Число T, удовлетворяющее указанному условию, называют периодом функции у = f(x). Отсюда следует, что, поскольку для любого х справедливы равенства:
sin (x-2р) = sin x = sin (х+2р),
cos (x-2р)= cos x= cos (x+2р),
то функции у = sin х, у=cos х являются периодическими и число 2р служит периодом и той, и другой функции. Периодичность функции — это есть девятое свойство функций.
Все
тригонометрические функции (синус,
косинус, тангенс и котангенс) относятся
к основным элементарным функциям. Сейчас
мы рассмотрим их графики и перечислим
свойства.
Тригонометрическим
функциям присуще понятие периодичности (повторяемости
значений функции при различных значениях
аргумента, отличных друг от друга на
величину периода 
,
где Т —
период), поэтому, в список свойств
тригонометрических функций добавлен
пункт «наименьший
положительный период».
Также для каждой тригонометрической
функции мы укажем значения аргумента,
при которых соответствующая функция
обращается в ноль.
Теперь
разберемся со всеми тригонометрическими
функциями по-порядку.
Функция
синус y
= sin(x).
Изобразим
график функции синус, его называют
«синусоида».
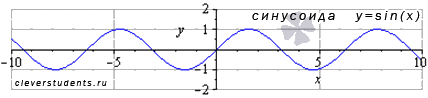
Свойства
функции синус y
= sinx.
Областью
определения функции синус является
все множество действительных чисел,
то есть, функция y = sinx определена
при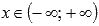
.Наименьший
положительный период функции синуса
равен двум пи: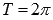
.Функция
обращается в ноль при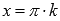
,
где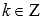
, Z –
множество целых чисел.Функция
синус принимает значения из интервала
от минус единицы до единицы включительно,
то есть, ее область значений есть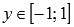
.Функция
синус — нечетная, так как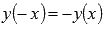
.Функция
убывает при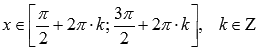
,возрастает
при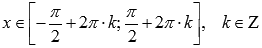
.Функция
синус имеет локальные максимумы в
точках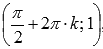
,
локальные
минимумы в точках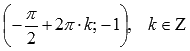
.Функция y = sinx вогнутая
при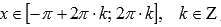
,
выпуклая
при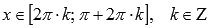
.Координаты
точек перегиба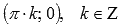
.Асимптот
нет.
Функция
косинус y
= cos(x).
График
функции косинус (его называют «косинусоида»)
имеет вид:
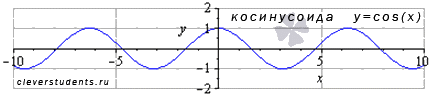
Свойства
функции косинус y
= cosx.
Область
определения функции косинус: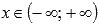
.Наименьший
положительный период функции y = cosx равен
двум пи: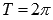
.Функция
обращается в ноль при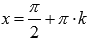
,
где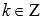
, Z –
множество целых чисел.Область
значений функции косинус представляет
интервал от минус единицы до единицы
включительно: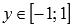
.Функция
косинус — четная, так как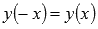
.Функция
убывает при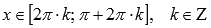
,
возрастает
при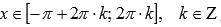
.Функция y = cosx имеет
локальные максимумы в точках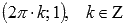
,
локальные
минимумы в точках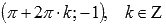
.Функция
вогнутая при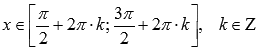
,
выпуклая
при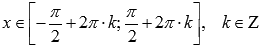
.Координаты
точек перегиба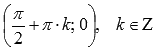
.Асимптот
нет.
Функция
тангенс y
= tg(x).
График
функции тангенс (его называют «тангенсоида»)
имеет вид:
Свойства
функции тангенс y
= tgx.
Область
определения функции тангенс: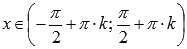
,
где
, Z –
множество целых чисел.
Поведение
функции y = tgx на
границе области определения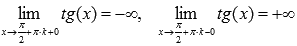
Следовательно,
прямые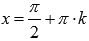
,
где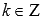
,
являются вертикальными асимптотами.Наименьший
положительный период функции тангенс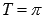
.Функция
обращается в ноль при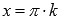
,
где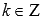
, Z –
множество целых чисел.Область
значений функции y = tgx: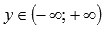
.Функция
тангенс — нечетная, так как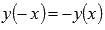
.Функция
возрастает при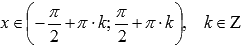
.Функция
вогнутая при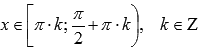
,выпуклая
при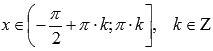
.Координаты
точек перегиба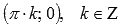
.Наклонных
и горизонтальных асимптот нет.
Функция
котангенс y
= ctg(x).
Изобразим
график функции котангенс (его называют
«котангенсоида»):
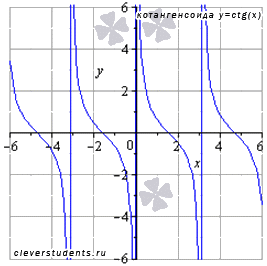
Свойства
функции котангенс y
= ctgx.
Область
определения функции котангенс: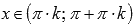
,
где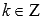
, Z –
множество целых чисел.
Поведение на
границе области определения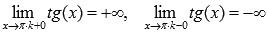
Следовательно,
прямые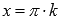
,
где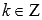
являются
вертикальными асимптотами.Наименьший
положительный период функции y = ctgx равен
пи: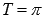
.Функция
обращается в ноль при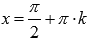
,
где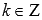
, Z –
множество целых чисел.Область
значений функции котангенс: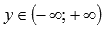
.Функция
нечетная, так как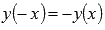
.Функция y = ctgx убывает
при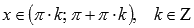
.Функция
котангенс вогнутая при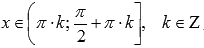
,
выпуклая
при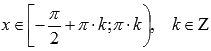
.Координаты
точек перегиба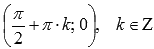
.Наклонных
и горизонтальных асимптот нет.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #