Какими свойствами обладают точка подвеса и центр качания маятника
Рассмотрим так называемый
математический маятник — материальную точку, подвешенную на невесомой нерастяжимой нити и совершающую колебания в вертикальной плоскости под действием силы тяжести.
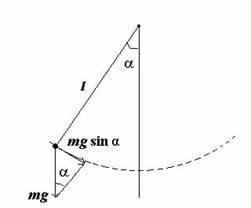
| Второй закон | для такого маятника запишется так: |
,
или
Сравнивая
его с дифференциальным уравнением гармонических
колебаний (2), увидим, что оно по виду будет совпадать, если sina заменить на
a,
что можно сделать при малых a. Следовательно, колебания математического маятника
можно считать гармоническими только при малых углах отклонения от положения
равновесия.
Итак, гармонические колебания математического маятника описываются уравнением
Сравнивая его с уравнение (2), находим, что циклическая частота собственных колебаний математического маятника
Рассмотрим так называемый физический маятник, то есть реальное физическое тело, совершающее колебания относительно горизонтальной оси
O (оси качания), не проходящей через центр инерции тела C.
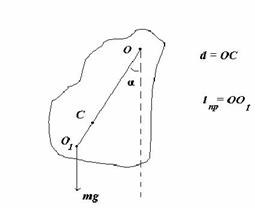
На рисунке обозначено:
ось качания маятника — неподвижная горизонтальная ось О, не проходящая через центр тяжести тела;
точка подвеса маятника О — пересечение оси качания с вертикальной плоскостью, проходящей через центр тяжести маятника и перпендикулярной оси качания;
приведенная длина физического маятника L пр — длина математического маятника, имеющего такой же период колебаний;
центр качания физического маятника — О1.
Согласно второму закону Ньютона, уравнение движения такого маятника запишется следующим образом:
где J — момент инерции маятника относительно точки О.
Видно, что колебания физического маятника также будут гармоническими только при малых углах качания, то есть когда
sin
a
@
a. В этом случае уравнение движения (колебаний) маятника совпадает по виду с дифференциальным уравнением свободных колебаний:
Сравнивая это уравнение с уравнением свободных колебаний, найдем частоту колебаний физического маятника:
Из определения приведенной длины физического маятника найдем, что:
Здесь Jc — момент инерции относительно центра масс тела С.
Центр качания О1 обладает тем свойством, что, если ось качания провести через
О1, частота колебаний маятника не изменится, а центр качания будет располагаться в точке
О. То есть точки О и О1 обладают свойством взаимозаменяемости. Проверить это утверждение следует следующим образом: необходимо вычислить частоту колебаний маятника, когда ось качания проходит через точки
О и О1 и сравнить эти формулы.
Рассмотрим пружинный маятник (или в общем случае так называемый
линейный гармонический осциллятор), то есть материальную точку массой
m, совершающую линейные гармонические колебания под действием упругой силы
F:
F = — k x (для пружины это — закон Гука).
Второй закон Ньютона для такого маятника запишется так:
,
или
Последнее уравнение является уравнением свободных колебаний, откуда сразу находим период колебаний:
Физическим маятником называется твердое тело, способное совершать колебания вокруг неподвижной точки, не совпадающей с его центром инерции (рис. 46а). В положении равновесия центр инерции С находится под точкой подвеса 0 маятника на одной с ней вертикали. При отклонении маятника от положения равновесия на угол j возникает вращательный момент сил, стремящийся вернуть маятник в положение равновесия. Этот момент равен
М = –mglsinj,
где m –масса маятника, а l–расстояние между точкой подвеса ицентром масс маятника. Знак «–» означает, что момент сил направлен против углового смещения. Уравнение вращательной динамики принимает вид:
b = М / I = – (mgl/ I) sin j,
где I – момент инерции маятника относительно оси, проходящей через точку подвеса. В случае малых колебаний (j≤ 5°) это уравнение переходит в дифференциальное уравнение собственных незатухающих колебаний:
,
решением которого является функция:
j = А cos (w0t + a0),
где через w0 обозначена угловая частота колебаний:
w0 = (mgl/ I)1/2.
Таким образом, при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, угловая частота w0 которых зависит от массы маятника, момента инерции маятника относительно оси вращения и расстояния между осью вращения и центром инерции маятника. Период колебаний физического маятника определяется выражением:
.
Из сопоставления формул 
и 
следует, что математический маятник с длиной lпр = (I/ml) имеет такой же период колебаний, как и данный физический маятник. Величину lпр = (I/ml) называют приведенной длиной физического маятника. Итак, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка 0′ на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника. По теореме Штейнера момент инерции маятника I может быть представлен в виде
I = I0 + ml2,
где I0 – момент инерции относительно оси, параллельной оси вращения и проходящей через центр инерции маятника.
Подставив I = I0 + ml2 в lпр = (I/ml) , получаем: lпр = (I0/ml) + l , откуда следует, что приведенная длина lпр всегда больше длины l, так что точка подвеса 0 и центр качания 0′ лежат по разные стороны от центра инерции С (центра масс). Подвесим маятник в центре качания 0′.Приведенная длина в этом случае будет равна: lпр‘ = (I0/ml‘) + l‘ , где l‘ – расстояние между первоначальным центром качания и центром инерции маятника. Учитывая, что l‘ = lпр – l, имеем:
lпр‘ = I0/m(lпр – l) + lпр – l = lпр + [(I0 + ml2) – mlпрl] /m(lпр – l).
Выражение, стоящее в квадратных скобках, равно нулю, поскольку I0 + ml2 = I – это момент инерции относительно первоначальной оси вращения; этой же величине равно выражение mlпрl.Таким образом, мы приходим к выводу, что при подвешивании маятника в центре качания приведенная длина, а значит, и период колебаний будут теми же, что и вначале. Следовательно, точка подвеса 0 и центр качания 0′ обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.
На свойстве взаимности основано определение ускорения силы тяжести с помощью, так называемого оборотного маятника (рис. 46б). Оборотным называется такой маятник, у которого имеются две параллельные друг другу, закрепленные вблизи его концов опорные призмы П1 и П2, за которые он может поочередно подвешиваться. Вдоль маятника могут перемещаться и закрепляться на нем тяжёлые грузы – чечевицы А и В. Перемещением грузов добиваются того, чтобы при подвешивании маятника за любую из призм период колебаний был одинаков. Тогда расстояние между опорными ребрами призм будет равно lпр. Измерив период колебаний маятника Т0 и определив lпр, при помощи формулы 
можно найти ускорение силы тяжести g:
.
Физическим маятником называется твердое тело, способное совершать
колебания вокруг неподвижной точки, не совпадающей с его центром инерции
Физическим маятником называется твердое тело, способное
совершать колебания вокруг неподвижной точки, не совпадающей с его центром
инерции. В положении равновесия центр инерции маятника С под точкой подвеса
маятника О, на одной с ней вертикали (рис. 170). При отклонении маятника от
положения равновесия на угол возникает вращательный момент,
стремящийся вернуть маятник в положение равновесия. Этот момент равен
(67.1) |
где m— масса
маятника» а l-расстояние между точкой подвеса и центром инерции маятника. Знак
«-» имеет то же значение, что и в случае формулы (66.1). Обозначив момент
инерции маятника относительно оси, проходящей через точку подвеса, буквой lможно написать:
(67.2) |
Рис.
170.
В случае малых колебаний (67.2) переходит в уже известное
нам уравнение:
(67.3) |
Через обозначена в данном случае следующая
величина:
(67.4) |
Из уравнений (67.3) и (67.4) следует, что при малых
отклонениях от положения равновесия физический маятник совершает гармонические
колебания, частота которых зависит от массы маятника, момента инерции маятника
относительно оси вращения и расстояния между осью вращения и центром инерции
маятника. В соответствии с (67.4) период колебания физического маятника
определяется выражением
(67.5) |
Из сопоставления формул (66.6) и (67.5) получается, что
математический маятник с длиной
(67.6) |
будет иметь такой период колебаний,
как и данный физический маятник. Величину (67.6) называют приведенной длиной
физического маятника. Таким образом, приведенная длина физического маятника —
это длина такого математического маятника, период колебаний которого совпадает
с периодом данного физического маятника
Точка на прямой, соединяющей точку подвеса с центром
инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром
качания физического маятника (см. точку О’ на рис.107).
По теореме Штейпера момент инерции маятника l может быть
представлен в виде
(67.7) |
где l0 — момент инерции
относительно оси, параллельной оси вращений и проходящей через центр инерции
маятника. Подставив (67.7) в формулу (67.6), получаем:
(67.8) |
Из (67.8) следует, что приведенная длина всегда больше 1,
так что точка подвеса и центр качания лежат по разные стороны от центра
инерции.
Подвесим маятник в точке, совпадающей с центром качания О’ В
соответствии с (67.8) приведенная длина в этом случае будет равна
(67.9) |
где l’ — расстояние между
первоначальным центром качания и центром инерции маятника. Учитывая, что , выражение (07.9)
можно записать следующим образом:
Выражение, стоящее в квадратных скобках, равно нулю.
Действительно, равно
I—моменту инерции относительно первоначальной оси
вращения; этой же величине в соответствии с (67.6) равно выражение mllпр. Таким образом, мы приходим к выводу,
что при подвешивании маятника в центре качания приведенная длина, а значит, и
период колебаний будут теми же, что и вначале. Следовательно, точка подвеса и
центр качания обладают свойством взаимности при переносе точки подвеса в центр
качания прежняя точка подвеса .становится новым центром качания.
На установленном нами свойстве взаимности основано
определение ускорения силы тяжести с помощью так называемого оборотного
маятника. Оборотным называется такой маятник, у которого имеются две
параллельные друг другу, закрепленные вблизи его концов опорные призмы, за
которые он может поочередно подвешиваться. Вдоль маятника могут перемещаться и
закрепляться на нем тяжёлые грузы. Перемещением грузов добиваются того, чтобы
при подвешивании маятника за любую из призм период колебаний был одинаков.
Тогда расстояние между опорными ребрами призм будет равно lпр.
Измерив период колебаний маятника и зная l™, можно по Формуле
найти ускорение силы тяжести g.
Лабораторная работа № 5
изучение закона колебаний
физического маятника
5.1. Цель работы: Экспериментальная проверка закона колебаний физического маятника при малой угловой амплитуде. Освоить метод определения ускорения силы тяжести с помощью физического маятника.
5.2. Краткое теоретическое введение
5.2.1. Период колебаний физического маятника
Физическим маятником называется твердое тело произвольной формы, укрепленное на неподвижной горизонтальной оси (не проходящей через его центр масс) и способное совершать колебания относительно этой оси.
В состоянии устойчивого равновесия физического маятника линия, проходящая через точки подвеса «О» и центра масс «С», направлена вертикально (см. рис.5.1).
Если маятник отклонить от положения равновесия на некоторый угол a и отпустить, то он будет совершать колебательное движение (рис.5.1) под действием момента силы тяжести относительно оси вращения. Проекция на ось вращения момента силы тяжести равна:
, (5.1)
где m – масса маятника,
g – ускорение свободного падения,
a – расстояние от точки подвеса «О» до центра масс «С».
Уравнение движения (уравнение моментов) физического маятника в проекции на ось вращения имеет следующий вид (см. Приложение):
(5.2)
где I – момент инерции маятника относительно оси вращения.
Если угол отклонения достаточно мал (a<5°), то можно приближённо принять, что . Тогда, вводя обозначение
(5.3)
уравнение движения маятника (5.2) можно привести к виду:
(5.4)
Решением данного дифференциального уравнения является гармоническая функция вида:
(5.5)
где a – угловая амплитуда колебания (в радианах),
j – начальная фаза колебания,
j = w0 t+j – полная фаза колебания.
Выясним физический смысл введённой нами величины w. Так как функция является периодической с периодом равным j2 ‑ j1 = 2p, то время Т = t2 – t1, необходимое для совершения одного полного колебания, можно найти из условия :
откуда
(5.6)
Таким образом, время Т одного полного колебания, называемое периодом колебаний, определяется выражением:
(5.7)
Число колебаний в единицу времени называется частотой и обозначается n. Тогда
n=1/T.
Круговой (или циклической) частотой называется число колебаний за время 2pсекунд, то есть круговая частота равна:
.
Из сравнения с формулой (5.7) видно, что введенная нами выше величина w есть ни что иное, как круговая частота.
Сравнивая выражение (5.7) с формулой для периода колебаний математического маятника
, (5.8)
можно сделать вывод, что математический маятник, у которого длина
(5.9)
будет иметь тот же период колебаний, что и данный физический маятник
Величина l0 называется приведенной длиной физического маятника.
Приведенная длина физического маятника равна длине математического маятника с периодом колебаний, равным данному физическому маятнику.
5.2.2. Центр качания.
Точка, которая лежит на прямой, проходящей через точку подвеса и центр масс, и находится на расстоянии приведенной длины от точки подвеса, называется центром качания (рис. 5.1., точка 0’).
По теореме Гюйгенса — Штейнера (см. Приложение к лабораторной работе № 12) момент инерции твердого тела относительно произвольной оси равен
I= I0 + ma2 (5.10)
где I — момент инерции тела относительно оси, проходящей через центр масс.
Подставив в это равенство выражение (5.9) и разрешив его относительно l,, получим:
(5.11)
Из этой формулы видно, что приведенная длина равна сумме расстояния от точки подвеса до центра масс (а) плюс некоторая добавка , то есть центр качания «O’ » лежит ниже центра масс «C» (см. рис.5.1).
Рис.5.1.
Обозначим расстояние от центра масс «С» до центра качания «O‘ » через b, тогда
.
Отсюда .
Подставив эти выражения в (5.11), будем иметь:
. (5.12)
Из соотношений (5.11) и (5.12) видно, что если маятник подвесить за центр качания, то период колебаний не изменится. Таким образом, при переносе точки подвеса в центр качания прежняя точка подвеса становится центром качания, т. е. точка подвеса и центр качания обратимы.
5.2.3. Зависимость периода колебаний физического маятника от расстояния между точкой подвеса и центром масс
Подставив (5.10) в (5.7), получим зависимость периода Т колебаний физического маятника от расстояния а между точкой подвеса «О» и центром масс «С»:
(5.13)
На рис. 5.2. качественно изображена зависимость (5.13). При а® (точка подвеса приближается к центру масс) период колебаний Т стремится к бесконечности, что соответствует безразличному равновесию. С удалением точки подвеса от центра масс, период колебаний Т маятника сначала уменьшается, а затем снова возрастает и с дальнейшим увеличением а опять стремится к бесконечности.
В случае а®¥ вторым слагаемым под корнем в выражении (5.13) можно пренебречь по сравнению с первым, тогда будем иметь:
Последняя формула соответствует периоду колебаний математического маятника. Действительно, пределу а®¥ соответствует пренебрежение размерами самого маятника по сравнению с расстоянием а от точки подвеса до центра масс — это и есть определение математического маятника.
Период колебаний физического маятника принимает минимальное значение на некотором расстоянии а* от точки подвеса до центра масс. Найти это расстояние а* и соответствующий ему период колебаний Тmin можно из условия экстремума:
.
Отсюда, используя (5.13), получим следующие выражения:
, (5.14)
5.2.4. Метод определения ускорения свободного падения с помощью стержневого маятника
Предлагаемый метод определения ускорения силы тяжести основан на использовании формулы (5.8):
. (5.15)
Приведенная длина l0 определяется графически с помощью экспериментально полученной зависимости периода колебаний физического маятника от расстояния между точкой подвеса и центром масс, качественно изображенной на рис.5.2. Как видно, эта кривая состоит из двух ветвей, симметрично расположенных относительно оси ординат (ось Т).
Рис.5.2.
5.3. Описание экспериментальной установки
Приборы и принадлежности: стержневой маятник, секундомер, электромеханический счетчик числа колебаний.
Общий вид универсального маятника представлен на рис.5.3. Основание (1) оснащено регулируемыми ножками (2), которые позволяют провести выравнивание прибора. В основании закреплена колонка (3), на которой зафиксированы верхний кронштейн (4) и нижний кронштейн (5) с фотоэлектрическим датчиком (6).
С одной стороны кронштейна (4) находится физический маятник (8), выполненный в виде стального стержня длиной 590 мм и диаметром 10 мм, на котором фиксируется призменный подвес (12).
На стержне через 10 мм выполнены кольцевые канавки для точной фиксации подвеса, который можно перемещать вдоль стержня и фиксировать на любой канавке с помощью винта.
Нижний кронштейн (5) с фотоэлектрическим датчиком (6) можно также перемещать вдоль колонки (3) и фиксировать в таком положении, чтобы конец стержня (8), пересекая световой луч датчика, не соударялся с кронштейном (5).
|
|
Рис.5.3.
На лицевой панели прибора расположены кнопки управления:
«сеть» — выключатель сети;
«сброс» — сброс показаний секундомера и запуск нового отсчета времени и числа периодов колебаний;
«стоп» — останов отсчета времени и периодов колебаний, а также цифровые индикаторы количества периодов и полного времени колебаний.
Электронная схема прибора позволяет производить отсчет числа периодов колебаний от 0 до 100 и времени колебаний с помощью цифрового электронного секундомера в пределах от 0 до 100с с погрешностью ± 0,001с.
5.4. Порядок выполнения работы
5.4.1. Подготовка к измерениям.
· установите нижний кронштейн (5) в крайнее нижнее положение, а вершину призмы подвеса на четвертую от края канавку кольцевой проточки стержня (8) так, чтобы нижний конец установленного в ролики стержня проходил в разрезе фотодатчика (6);
· подключите прибор к питающей сети;
· нажмите кнопку «сеть», проверьте наличие свечения лампы фотодатчика (6) и высвечивание нулей на цифровых индикаторах.
5.4.2. Проведение измерений
5.4.2.1. Предварительный опыт.
· Отклоните стержень (8) от вертикального положения равновесия на небольшой угол и отпустите. Стержень должен свободно совершать колебания, пересекая световой луч фотодатчика (6). Начальное угловое отклонение a нужно брать как можно меньше, однако его нельзя сделать сколь угодно малым – необходимо, чтобы за 10-20 периодов колебаний они ещё не затухали настолько, что световой луч датчика перестанет периодически прерываться колеблющимся стержнем.
· Нажмите и отпустите кнопку «сброс». Проверьте визуально работу секундомера и счётчика числа колебаний, который должен срабатывать на каждое второе пересечение луча фотодатчика. После отсчета 10-20 колебаний остановите измерения нажатием кнопки «стоп».
· Повторите опыты при различных углах отклонения a и подберите такой угол, при дальнейшем уменьшении которого период колебаний не изменяется. В дальнейших измерениях следует придерживаться этого угла.
5.4.2.2. Основные измерения.
· Подготовьте таблицу для записи результатов измерений, предусмотрев колонки для записи:
1) номера iкольцевой проточки, напротив которого установлена призма подвеса;
2) расстояния аiот точки подвеса до центра масс;
3) 3-х измерений времени ti 5 — 10 периодов колебаний и среднего значения <ti>;
4) периода Ti колебаний;
Число необходимых измерений – 25.
· Перемещая призму подвеса последовательно на одну проточку(10мм), двигаясь к центру масс, проведите измерения времени 10 периодов колебаний маятника по 3 раза для каждого положения призмы подвеса. Занести результаты в таблицу. Кронштейн (5) также надо перемещать вверх так, чтобы нижний конец стержня пересекал луч фотодатчика.
Узнай стоимость своей работы
Бесплатная оценка заказа!
5.5. Математическая обработка результатов измерений
5.5.1. По средним значениям <ti> определить период колебаний Ti и занести эти значения в таблицу.
5.5.2. Построить график зависимости периода колебаний Тi от расстояния между точкой подвеса и центром масс аi, используя все экспериментальные точки.
5.5.3. Построить в более крупном масштабе (увеличив масштаб Т в 20¸50 раз) отдельно область зависимости Т=f(а), в которой одному и тому же периоду Тi отвечают два значения величины аi.
5.5.4. Проведя 5-6 горизонтальные прямые, найти значения а1iи a2i, соответствующие точкам пересечения этих прямых с графиком Т=f(а) и определить приведённые длины li=a1i+a2i для каждого значения Ti.
5.5.5. Подставив полученные значения li и Ti в формулу (5.15), найти экспериментальные значения ускорения свободного падения.
5.5.6. Определить среднее значение <g> и доверительный интервал Dg по методу прямых измерений для заданного значения доверительной вероятности.
5.5.7. Сравниваем полученное значение с табличным значением для города Алматы (g=9,804 м/с2).
5.5.8. Используя формулу для момента инерции тонкого стержня относительно оси вращения, перпендикулярной стержню, проходящей через центр масс:
(где m— масса стержня, а l— его длина), рассчитать по формулам (5.14) теоретическое значение минимального периода колебаний Tmin и соответствующее ему расстояние а* от точки подвеса до центра масс; сравнить их с полученными экспериментально по графику.
5.6. Вопросы для самоконтроля
5.6.1. Дайте определение физического и математического маятников.
5.6.2. Как выглядят кривые зависимости периода колебаний от расстояния а между точкой подвеса и центром масс для математического и физического маятников, изображенных на одном и том же графике? Объясните, почему именно так?
5.6.3. Остается ли момент инерции физического маятника одинаковым относительно осей, проходящих через разные точки подвеса? Почему?
5.6.4. Каков физический смысл термина «приведенная длина физического маятника»?
5.6.5. Каким образом может влиять масса и форма подвеса маятника на его движение? Приведет ли учет наличия подвеса к увеличению или уменьшению периода колебаний?
5.6.6. Объясните, почему кривая зависимости периода T колебаний от величины а на рис.5.2. симметрична относительно центра масс, хотя сам физический маятник такой симметрией может и не обладать?
5.7. Литература
5.7.1. Ñèâóõèí Ä.Â. Îáùèé êóðñ ôèçèêè, Ò.1.-Ì.: Íàóêà, 1974.
5.7.2. Ãîëüäèí Ë.Ë. Ðóêîâîäñòâî ê ëàáîðàòîðíûì çàíÿòèÿì ïî ôèçèêå. -Ì.: Íàóêà, 1973.
П Р И Л О Ж Е Н И Е
Основным уравнением движения твердого тела, закрепленного в точке, в частности способного совершать лишь вращение вокруг неподвижной оси, является уравнение моментов:
(П1)
где — момент импульса тела относительно точки закрепления,
— момент внешних сил относительно той же точки.
Для тела, вращающегося вокруг неподвижной оси, имеем:
(П2)
где I— момент инерции тела относительно оси вращения;
— вектор угловой скорости вращения.
Поэтому, подставляя (П2) в (П1), получим основное уравнение вращательного движения в следующем виде:
. (П3)
Принимая во внимание, что по определению есть угловое ускорение и обозначив его , уравнение (П3) запишем в виде:
Существует лишь одна сила (если пренебречь трением), создающая момент относительно оси вращения — это сила тяжести, приложенная к центру масс, поэтому
, (П4)
где — радиус-вектор, проведенный из точки О, расположенной на оси вращения, в центр масс тела (на рис. 5.1. ). Вектор направлен перпендикулярно плоскости рисунка от нас в соответствии с правилом правого буравчика (правой руки), примененного для векторного произведения (П4).
Проекция М вектора на ось вращения равна
(П5)
Знак «минус» в выражении (П.5) показывает, что эта проекция направлена против выбранного направления углового перемещения при отклонении от положения равновесия.
Таким образом, уравнение (П.3), записанное в проекции на ось вращения примет вид:
или в других обозначениях
(П6)
где — вторая производная по времени от угла поворота вокруг оси вращения (угловое ускорение);
— положительная постоянная.
Уравнение (П6) описывает колебания физического маятника вокруг неподвижной оси вращения.