Какими свойствами обладают спектры периодических сигналов
2.1. Спектры
периодических сигналов
Периодическим сигналом (током или
напряжением) называют такой вид воздействия, когда форма сигнала повторяется
через некоторый интервал времени T,
который называется периодом. Простейшей формой периодического сигнала является
гармонический сигнал или синусоида, которая характеризуется амплитудой,
периодом и начальной фазой. Все остальные сигналы будут негармоническими или
несинусоидальными. Можно показать, и практика это доказывает, что, если
входной сигнал источника питания является периодическим, то и все остальные
токи и напряжения в каждой ветви (выходные сигналы) также будут периодическими.
При этом формы сигналов в разных ветвях будут отличаться друг от друга.
Существует общая методика исследования
периодических негармонических сигналов (входных воздействий и их реакций) в
электрической цепи, которая основана на разложении сигналов в ряд Фурье. Данная
методика состоит в том, что всегда можно подобрать ряд гармонических (т.е.
синусоидальных) сигналов с такими амплитудами, частотами и начальными фазами, алгебраическая
сумма ординат которых в любой момент времени равна ординате исследуемого
несинусоидального сигнала. Так, например, напряжение u на рис. 2.1. можно заменить суммой напряжений и , поскольку в любой момент времени имеет место тождественное
равенство:. Каждое из слагаемых представляет собой синусоиду, частота
колебания которой связана с периодом T
целочисленными соотношениями.
Для рассматриваемого
примера имеем период первой гармоники совпадающим с периодом негармонического
сигнала T1=T,
а период второй гармоники в два раза меньшим T2=T/2,
т.е. мгновенные значения гармоник должны быть записаны в виде:
Здесь амплитуды колебаний гармоник равны между собой (), а начальные фазы равны нулю.
Рис. 2.1. Пример сложения первой и второй
гармоники
негармонического сигнала
В электротехнике гармоническая
составляющая, период которой равен периоду негармонического сигнала, называется
первой или основной гармоникой сигнала. Все остальные составляющие называются
высшими гармоническими составляющими. Гармоника, частота которой в k раз больше
первой гармоники (а период, соответственно, в k раз меньше), называется
k — ой гармоникой.
Выделяют также среднее значение функции за период, которое называют нулевой гармоникой. В общем случае ряд
Фурье записывают в виде суммы бесконечного числа гармонических составляющих
разных частот:
(2.1) |
где k — номер
гармоники; — угловая частота k —
ой гармоники;
ω1=ω=2π/T—
угловая частота первой гармоники; — нулевая гармоника.
Для сигналов часто встречающихся форм
разложение в ряд Фурье можно найти в специальной литературе. В таблице 2
приведены разложения для восьми форм периодических сигналов. Следует отметить,
что приведенные в таблице 2 разложения будут иметь место, если начало системы
координат выбраны так, как это указано на рисунках слева; при изменении начала
отсчета времени t будут изменяться
начальные фазы гармоник, амплитуды гармоник при этом останутся такими же. В
зависимости от типа исследуемого сигнала под V следует понимать либо величину,
измеряемую в вольтах, если это сигнал напряжения, либо величину, измеряемую в
амперах, если это сигнал тока.
Разложение
в ряд Фурье периодических функций
Таблица
2
График f(t) | Ряд Фурье функции f(t) | Примечание |
| k=1,3,5,… | |
| k=1,3,5,… | |
| k=1,3,5,… | |
| k=1,2,3,4,5 | |
| k=1,3,5,… | |
| k=1,2,3,4,5 | |
| S=1,2,3,4,.. | |
| k=1,2,4,6,.. |
Сигналы 7 и 8 формируются из синусоиды
посредством схем, использующих вентильные элементы.
Совокупность гармонических составляющих,
образующих сигнал несинусоидальной формы, называется спектром этого
негармонического сигнала. Из этого набора гармоник выделяют и различают амплитудный и фазовый спектр. Амплитудным спектром называют набор амплитуд всех
гармоник, который обычно представляют диаграммой в виде набора вертикальных
линий, длины которых пропорциональны (в выбранном масштабе) амплитудным
значениям гармонических составляющих, а место на горизонтальной оси определяется
частотой (номером гармоники) данной составляющей. Аналогично рассматривают
фазовые спектры как совокупность начальных фаз всех гармоник; их также
изображают в масштабе в виде набора вертикальных линий.
Следует заметить, что
начальные фазы в электротехнике принято измерять в пределах от –1800
до +1800 . Спектры, состоящие из отдельных линий, называют линейчатыми или дискретными.
Спектральные линии находятся на расстоянии f
друг от друга, где f — частотный
интервал, равный частоте первой гармоники f
.Таким образом, дискретные спектры периодических сигналов имеют спектральные
составляющие с кратными частотами — f,
2f, 3f, 4f, 5f и т.д.
Пример
2.1. Найти амплитудный и фазовый спектр для сигнала прямоугольной формы,
когда длительности положительного и отрицательного сигнала равны, а среднее
значение функции за период равно нулю
u(t) = V при 0<t<T/2 | u(t) = -V при T/2<t<T |
Для сигналов простых часто используемых форм решение
целесообразно находить с помощью таблиц.
Рис. 2.2. Линейчатый амплитудный спектр
прямоугольного сигнала
Из разложения в ряд Фурье сигнала
прямоугольной формы (см. табл.2 — 1) следует, что гармонический ряд содержит
только нечетные гармоники, при этом амплитуды гармоник убывают пропорционально
номеру гармоники. Амплитудный линейчатый спектр гармоник представлен на рис.
2.2. При построении принято, что амплитуда первой гармоники (здесь напряжения)
равна одному вольту: B; тогда амплитуда
третьей гармоники будет равна B, пятой — B и т.д. Начальные
фазы всех гармоник сигнала равны нулю, следовательно, фазовый спектр имеет
только нулевые значения ординат.
Задача решена.
Пример 2.2.
Найти амплитудный и фазовый спектр для напряжения, изменяющегося по закону: при —T/4<t<T/4; u(t)
= 0 при T/4<t<3/4T. Такой сигнал
формируется из синусоиды посредством исключения (схемным путем с использованием
вентильных элементов) отрицательной части гармонического сигнала.
а) б)
Рис. 2.3. Линейчатый спектр сигнала
однополупериодного выпрямления: а)амплитудный; б)фазовый
Для сигнала однополупериодного
выпрямления синусоидального напряжения (см. табл.2 — 8) ряд Фурье содержит
постоянную составляющую (нулевую гармонику), первую гармонику и далее набор
только четных гармоник, амплитуды которых быстро убывают с ростом номера
гармоники. Если, например, положить величину V = 100 B, то, умножив каждое
слагаемое на общий множитель 2V/π , найдем
Приведем полученное выражение к принятой
в данном пособии синусоидальной форме записи слагаемых, используя известные из
математики формулы: cos(x) = sin(x+90˚) и -cos(x) = sin(x-90˚).
Окончательно получим:
(2.2) |
Амплитудный и фазовый спектры этого
сигнала изображены на рис.2.3а,б.
Задача решена.
В соответствии с теорией рядов Фурье
точное равенство негармонического сигнала сумме гармоник имеет место только при
бесконечно большом числе гармоник. Расчет гармонических составляющих на ЭВМ
позволяет анализировать любое число гармоник, которое определяется целью
расчета, точностью и формой негармонического воздействия. Если длительность
сигнала t
независимо от его формы много меньше периода T, то амплитуды гармоник будут убывать медленно, и для более
полного описания сигнала приходится учитывать большое число членов ряда. Эту
особенность можно проследить для сигналов, представленных в таблице 2 — 5 и 6,
при выполнении условия τ
<<T. Если негармонический
сигнал по форме близок к синусоиде (например, сигналы 2 и 3 в табл.2), то
гармоники убывают быстро, и для точного описания сигнала достаточно
ограничиться тремя — пятью гармониками ряда.
к содержанию
Теоретическое
введение
Частоты сигнала
Спектры сигналов
Колебательный контур
Вопросы
для самопроверки
1. Спектр периодического
сигнала
Рассмотрим общие
свойства спектров периодических
сигналов. Если сигнал V(t) периодичен
с периодом Т, то он разлагается в ряд
Фурье /2/ согласно соотношениям:
(1.1.)
wi
= iw1
где
—
основная циклическая частота сигнала,
частота первой гармоники, i – номер гармоники,wi — циклическая частота i-ой
гармоники,
(1.2.)
Из
приведенных соотношений видно:
а) Перемещение оси
абсцисс вверх или вниз равносильно
прибавлению некоторой постоянной
величины ко всем значениям V(t). Такое
преобразование изменяет среднее
значение — постоянную составляющую a0 , и не влияет на
амплитуды и фазы гармоник. Так можно
утверждать, что, например, спектр
сигналов, приведенных на рис. 1,
отличается только постоянной
составляющей. Заштрихованные площади
должны быть равными, тогда a0 — среднее значение.
Рис.1.
Сигналы, отличающиеся только величиной ао
б) Спектр периодического сигнала
дискретен, он состоит из гармоник с
частотами f=n/T, где n -любое целое
число, f в герцах. Никаких
других частот, кроме данных в
периодическом сигнале быть не может, но
вовсе не обязательно, чтобы в каждом
конкретном сигнале существовали все
возможные составляющие: для некоторых
гармоник часть коэффициентов Ai и Bi
может обращаться в ноль, т. е.
соответствующие гармоники отсутствуют.
Иногда
обращение в ноль части гармоник можно
увидеть непосредственно по форме
сигнала без обращения к формулам:
1)
Если сигнал представляет собой
гармонику, то, естественно, в его составе
нет никаких других гармоник, и он
характеризуется только одной частотой.
2)
Если при соответствующем выборе начала
отсчета времени сигнал представляет
собой четную функцию, т. е. V(t)=V(-t), то в соотношениях (1.2.): V(t)Sin(wit)- нечетная
функция (Sin -нечетная), а V(t)Cos(wit) — четная
функция. Тогда:
(1.3.)
(1.4.)
т. е. сигналы
разлагаются только по косинусам.
Физически это означает, что в точке
принятой за начало отсчета, все
гармоники одновременно имеют экстремум:
Максимум, если Bi окажется
положительным, и минимальным, если Bi —
отрицательным. На рис. 2 приведены
примеры таких сигналов. На рисунке Т1-длительность
импульса
t:
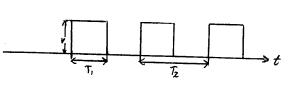
Рис.2. Примеры
сигналов, разлагающихся только по
косинусам
Если
сигнал представляет собой нечетную
функцию времени: V(t)=—V(-t), тоV(t)Sinwit – четная
функция (оба сомножителя нечетные), а V(t)Coswit
–
нечетная функция. Поэтому в (1.2.):
Разложение
в этом случае ведется только по синусам.
Т. е. в точке принятой за t=0 все гармоники проходят
через ноль.
3)
Если сигнал можно представить себе как
сумму положительных и отрицательных
импульсов, одинаковых по величине и
форме и сдвинутых на половину периода,
то такие сигналы не имеют в своем
составе четных гармоник.
Это легко показать из простых
рассуждений. Представим исходный сигнал,
как сумму двух сигналов, один из которых
(V1) состоит из
положительных, а другой (V2)
из отрицательных импульсов рис. 3 и
разложим в спектр каждый из этих
сигналов.
Рис.3.
Сигнал, не содержащий четных гармоник и
его составляющие
Сигналы
V1
и V2
имеют одинаковый период, величину и
форму, поэтому входящие в их состав
гармоники будут иметь одинаковые
частоты и амплитуды. Что касается
фазовых соотношений, то тут ситуация для
четных и нечетных гармоник различна. Для
четных гармоник сдвиг фаз на полпериода
основной частоты соответствует сдвигу
на целое число периодов рассматриваемой
гармоники, т. е. не меняет ее фазу. Таким
образом, фазы четных гармоник,
составляющих V1 и V2 оказываются
противоположными (импульсы
противоположной полярности) и
соответствующие гармоники
компенсируются, т. е. они отсутствуют в
суммарном сигнале V. Для нечетных
гармоник сдвиг фаз на полпериода
основной частоты соответствует сдвигу
фаз на целое число периодов плюс еще
полпериода частоты данной гармоники,
что изменяет фазу на
. C учетом противоположной
полярности импульсов эти гармоники
оказываются в фазе и их амплитуды
удваиваются при сложении.
Мы
отмечали, что смещение оси абсцисс вверх
или вниз меняет только постоянную составляющую
сигнала. Поэтому, проверяя сигнал на
наличие четных гармоник, можно мысленно
осуществлять такое смещение. На рис. 3
приведены еще два сигнала, не содержащие
четных гармоник:
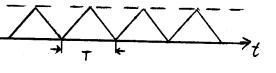
Рис.4. Примеры
сигналов, не содержащих четных гармоник
В первом сигнале
условием отсутствия четных гармоник
является то, что длительность должна
быть в два раза меньше периода. Во втором
случае время возрастания и убывания
напряжения должны быть равны. Тогда при
смещении оси времени на высоту, равную
среднему значению сигнала, мы получим,
что части сигнала, расположенные по
разные стороны оси равны и смещены
относительно друг друга на половину
периода. Следовательно, как было
рассмотрено ранее, получается обнуление
каждой четной гармоники за счет «разно
полярности» этих частей сигнала.
в) Количество гармоник в
ряде Фурье теоретически бесконечно и
полоса частот, которую он занимает, не
ограничена сверху. Однако так как общая
мощность сигнала всегда ограничена, то
для всех реальных сигналов существует
тенденция к постепенному уменьшению
амплитуд гармоник по мере увеличения их
номера. Соответственно при передаче
сигнала с заданной степенью точности
можно пренебрегать высокими, достаточно
слабыми гармониками, не передавать их,
ограничивая полосу пропускания сверху.
Требования к полосе частот зависят от
типа сигнала и заданного уровня
точности его воспроизведения. Сущность
этих требований раскрывается при
рассмотрении программного обеспечения,
которое прилагается к методическому
пособию в электронном варианте в виде
ссылки.
Далее
Made by potemkin.
Содержание
Обнаружили ошибку?
Выделите ее мышью
и нажмите
Вводные замечания
В
предыдущем разделе
было рассмотрено разложение периодических сигналов в ряд Фурье.
Были приведены выражения для ряда Фурье в тригонометрической и комплексной форме,
а также введено понятие спектра периодического сигнала.
Показано, что спектр периодического сигнала 
представляет собой
дискретную (линейчатую) функцию 
, определенную на равноотстоящей сетке частот
, 
В данном разделе мы рассмотрим некоторые свойства спектров периодических сигналов.
Как мы увидим позже, аналогичными свойствами обладают преобразование Фурье
непериодических сигналов, а также дискретное преобразование Фурье.
Свойство линейности
Пусть имеются два периодических сигнала 
и 
с равными периодами повторения 
,
причем оба сигнала удовлетворяют условиям Дирихле [1, стр. 165]. Сигналы и могут быть
представлены рядом Фурье с коэффициентами разложения 
и 
,
где 
,
Везде далее в этом разделе мы будем считать сигналы и периодическими
с равными периодами повторения , причем оба сигнала удовлетворяют условиям Дирихле.
Тогда сигнал 
также является периодическим сигналом с периодом ,
и может быть представлен рядом Фурье с коэффициентами:
(1)
Таким образом, спектр суммы периодических сигналов равен сумме их спектров.
Следствием свойства линейности является свойство умножения на константу.
Спектр сигнала 
, 
, равен:
(2)
Свойство циклического временного сдвига
Рассмотрим сигнал как результат циклического временного сдвига исходного сигнала , как это показано на рисунке 1 для положительных и отрицательных значений 
.
Рисунок 1. Циклический временной сдвиг сигнала
Циклический сдвиг характерен периодическим сигналам.
Спектр сигнала с циклическим временным сдвигом равен:
(3)
Введем замену переменной 
, тогда 
, 
, и выражение (3) преобразуется к виду:
(4)
Таким образом, циклический временной сдвиг периодического сигнала на величину
приводит к умножению спектра на фазовый множитель
. При этом амплитудный спектр 
не меняется, а фазовый спектр 
приобретает дополнительное линейное слагаемое.
Спектр циклической свертки сигналов
Пусть сигнал представляет собой циклическую (периодическую) свертку [2, стр. 362] сигналов и 
(5)
Тогда сигнал также периодический
с периодом и его спектр равен:
(6)
Поменяем порядок интегрирования, и используем свойство (4) циклического временного сдвига:
(7)
Таким образом, спектр периодического сигнала (5) пропорционален
произведению спектров 
и 
сигналов и .
Это одно из важнейших свойств спектрального анализа, которое позволяет анализировать
системы обработки сигналов в частотной области, заменяя трудоемкое вычисление свертки сигналов,
произведением их спектров.
Спектр произведения сигналов
Пусть сигнал 
представляет собой произведение сигналов и .
Сигнал также представляет собой периодический сигнал с периодом , и его спектр равен:
(8)
Подставим в (8) вместо сигнала его разложение в ряд Фурье:
(9)
Поменяем в (9) операции интегрирования и суммирования и получим:
(10)
Учтем, что
(11)
тогда окончательно спектр произведения периодических сигналов
(12)
равен линейной свертке спектров этих сигналов.
Симметрия спектра вещественного сигнала
Пусть представляет собой вещественный периодический сигнал.
Рассмотрим подробнее его спектр:
(13)
Амплитудный 
и фазовый 
спектр вещественного сигнала равен:
(14)
(15)
Анализируя выражения (14) и (15), можно обратить внимание,
что амплитудный спектр вещественного периодического сигнала всегда
симметричен относительно нулевой частоты, т.е. 
,
а фазовый спектр 
— антисимметричен.
Если же периодический сигнал 
— комплексный,
то симметрия спектра сигнала нарушается, что будет показано в следующем параграфе.
Свойство частотного сдвига
Пусть сигнал 
представляет собой
произведение сигналов и комплексной экспоненты с частотой
, где 
— произвольное целое число.
Выбор частоты 
обеспечивает
периодичность сигнала , поскольку на одном периоде
укладывается целое число оборотов комплексной экспоненты
.
Таким образом, сигнал удовлетворяет условиям Дирихле, и его спектр равен:
(16)
Умножение сигнала на комплексную экспоненту
переносит спектр сигнала на частоту 
.
При этом сигнал становится комплексным,
а его спектр — несимметричным относительно нулевой частоты.
На рисунке 2 показан пример частотного сдвига сигнала при умножении
на комплексную экспоненту при
рад/c.
Рисунок 2. Пример частотного сдвига спектра
при умножении сигнала на комплексную экспоненту
Можно видеть, что спектр смещенного по частоте сигнала
есть смещенная на частоту
копия спектра .
При этом важно отметить, что сам сигнал стал комплексным
(на графике показана отдельно реальная 
и мнимая
части сигнала),
его амплитудный спектр при этом перестал быть симметричным,
а фазовый — антисимметричным относительно нулевой частоты.
Рассмотрим теперь умножение сигнала не на комплексную экспоненту,
а на гармоническое колебание 
,
где 
, — произвольное целое число,
— произвольная начальная фаза.
В этом случае мы также сохраняем периодичность сигнала
, и его спектр равен:
(17)
Выразим 
через сумму комплексных экспонент , тогда:
(18)
Таким образом, умножение сигнала на гармоническое колебание приводит
к смещению спектра на частоты 
как в положительную,
так и в отрицательную области частот, уменьшению амплитуды
в положительной и отрицательной областях в два раза
и добавлению фазового множителя 
.
На рисунке 3 показан пример частотного сдвига сигнала при умножении
на 
при
рад/c (5 Гц), и 
рад.
Рисунок 3. Пример частотного сдвига периодической последовательности прямоугольных импульсов
при умножении на
Из рисунка 3 можно видеть, что спектр смещенного по частоте сигнала
есть сумма смещенных на частоты 
спектров половинной амплитуды.
При этом заметим, что вещественный сигнал остается вещественным
с симметричным амплитудным и антисимметричным фазовым спектром.
Равенство Парсеваля
Пусть имеется периодический сигнал , который представляет собой
изменяющееся во времени значение тока или напряжения.
Рассмотрим среднюю мощность 
выделяемую
на сопротивлении 1 Ом сигналом :
(19)
где 
— сигнал, комплексно-сопряженный .
Подставим в (19) вместо выражение ряда Фурье в комплексной форме:
(20)
Поменяем местами операции суммирования и интегрирования и получим:
(21)
Приравнивая (19) и (21), получаем равенство Парсеваля [3, стр. 39],
связывающее среднюю мощность периодического сигнала
во временной и частотной областях:
(22)
Из (22) следует, что средняя мощность, выделяемая на сопротивлении 1 Ом за один период повторения сигнала равна сумме квадратов
модулей спектральных составляющих этого сигнала. При этом суммирование идет для 
от минус бесконечности, до бесконечности. Это означает, что компоненты с отрицательными частотами 
, соответствующие отрицательным , также вносят вклад в среднюю мощность сигнала.
Если учесть, что у вещественного периодического сигнала амплитудный спектр является симметричным относительно нулевой частоты, то можно заключить, что спектральные составляющие в отрицательной области частот несут ту же мощность, что и спектральные составляющие с положительными частотами 
. Поэтому отрицательные частоты, которые появились при переходе к ряду Фурье в комплексной форме, это не просто математическая абстракция, а физическая сущность, несущая практически половину мощности вещественного сигнала.
Спектр производной исходного сигнала
Пусть сигнал представляет собой непрерывный дифференцируемый на всей числовой оси периодический сигнал (не имеет разрывов первого рода), чей спектр равен . Тогда сигнал 
также представляет собой периодический сигнал, удовлетворяющий условиям Дирихле и его спектр равен:
(23)
Используем правило интегрирования по частям [4, стр. 330]:
(24)
Учтем, что
(25)
Также в силу периодичности и непрерывности сигнала 
, и два первых слагаемых выражения (24) взаимно исключаются.
Окончательно:
(26)
Таким образом, спектр производной периодического сигнала равен спектру этого сигнала , умноженного на 
.
Наличие множителя приводит к тому, что спектр с ростом частоты затухает слабее чем спектр исходного сигнала . Поэтому изначально мы наложили ограничение на исходный сигнал: он должен быть непрерывным и дифференцируемым, тогда его спектр будет затухать быстрее чем 
, и умножение на не приведет к росту с увеличением частоты.
Спектр интеграла исходного сигнала
Пусть теперь представляет собой сигнал с нулевой постоянной составляющей. Спектр сигнала равен нулю на нулевой частоте: 
.
Тогда сигнал
(27)
представляет собой интеграл от сигнала , причем при , также является периодическим с периодом и удовлетворяет условиям Дирихле.
Заметим, что при наличии постоянной составляющей 
в сигнале , интегратор от минус бесконечности накопит бесконечную составляющую сигнала . На рисунке 4 показан пример периодического сигнала с нулевой постоянной составляющей и результат его интегрирования.
Рисунок 4. Пример периодического сигнала с нулевой постоянной составляющей и результат его интегрирования
Рассмотрим спектр сигнала . Для этого заметим, что сигнал 
ничто иное, как производная сигнала . Тогда использую свойство спектра производной сигнала (26) можно записать:
(28)
При 
, спектр рассчитывается без особого труда. Однако на частоте 
получаем неопределенность вида 
:
(29)
Раскроем неопределенность по правилу Лопиталя [4, стр. 257]:
(30)
По определению спектра
(31)
тогда продифференцируем левую и правую части (31) по переменной и найдем значение производной 
при 
:
(32)
Окончательно, спектр сигнала на нулевой частоте равен: