Какими свойствами обладают пределы

1. Функция не может
иметь более одного предела (при одной
и той же базе).
2. Предел постоянной
равен самой этой постоянной:
![]() ,
,
с – постоянная.
3. Предел суммы функций
равен сумме пределов этих функций:
![]()
4. Предел произведения
функций равен произведению пределов
этих функций:
![]()
Отсюда следует, что
постоянный множитель можно выносить
за знак предела:
![]()
5. Предел частного двух
функций равен частному пределов этих
функций (если предел делителя не равен
нулю):
![]()
6. (свойство предела
сложной функции) Если
![]() ,
,
то предел сложной функции![]() .
.
7. Если при базе В (т.е.
в некоторой окрестности точки х0или при достаточно больших х) f1(х)
< f2(х), то![]() .
.
Отметим, что в
перечисленных свойствах предполагается
существование пределов функций f1(х)
и f2(х), из чего следуют заключения
о значениях пределов суммы, произведения
или частного этих функций. Но при этом
из существования предела суммы,
произведения или частного функций не
обязательно следует, что существуют
пределы самих слагаемых, сомножителей
или делимого и делителя.
Например,
![]() ,
,
но при этом![]() не существует.
не существует.
Замечательные пределы
Для вычисления пределов
функций в некоторых случаях удобно
использовать так называемые замечательные
пределы(здесь рассматриваются без
доказательства).
Первый замечательный предел
![]()
Второй замечательный предел
Для числовой
последовательности (1 + 1/n)n:
![]()
Число е (число Эйлера)
– это иррациональное число, которое
приблизительно равно 2,718281. Это число
широко используется в математическом
анализе. График функции у = ехназывают экспонентой3.
Логарифм по основанию е называют
натуральным и обозначаютlnx.
Можно доказать, что
для функций f(x)
= (1 + 1/x)xиf(x) = (1 +x)1/x:

Непрерывность функции
Функция f(x) называется
непрерывнойв точкеx0,
если она удовлетворяет трем условиям:
1) определена в точке
(т.е. существует f(x0));
2) имеет конечный предел
при хх0;
3) этот предел равен
значению функции в точке х0,
т.е.
![]() .
.
Поясним определение
непрерывности следующим примером
(рисунок 2.10). На рисунке представлены
графики четырех функций y=f(x), первые
три из которых не являются непрерывными
в точкеx= 0, а четвертая
– является.
В самом деле, функция
(а) не является непрерывной в точке x= 0, так как вообще не определена в этой
точке (т.е. нарушено первое условие
непрерывности).
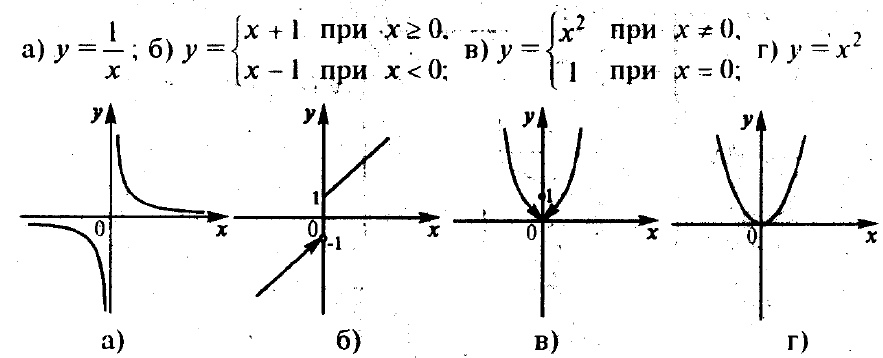
Д
Рисунок 2.10 –
Иллюстрация к определению непрерывности
функции
ля функции (б) в точкеx= 0 первое условие непрерывности
выполняется, но нарушается второе
условие – отсутствует предел функции
в этой точке (существуют только
односторонние пределы, не равные друг
другу:![]() ).
).
Поэтому функция (б) также не является
непрерывной.
Для функции (в) в точке
x = 0 выполняются первые два условия
непрерывности, но при этом
![]() ,
,
а f(0) = 1. Так как![]() ,
,
нарушается третье условие непрерывности,
и эта функция также не является
непрерывной.
А вот функция (г) в
точке x = 0является непрерывной,
так как в этом случае выполняются все
три условия непрерывности:![]() .
.
По-другому вышеприведенное
определение непрерывности функции
можно записать в виде:
![]() (для
(для
непрерывной функции возможна перестановка
символов предела и функции).
Слово «непрерывность»
применительно к функции используется
в связи с тем, что если функция непрерывна
в точке, то ее график в этой точке можно
провести, не отрываясь от листа, т.е. сам
график непрерывен.
Если функция не является
непрерывной в точке х0, то эту
точку называютточкой разрыва функции.
Точки разрыва могут
быть первого и второго рода.
В точке разрыва
первого родалибо существуют конечные
односторонние пределы функции слева и
справа, не равные друг другу (как на
рисунке 2.10 (б)), либо предел функции в
этой точке существует, но не равен
значению функции в этой точке (как на
рисунке 2.10 (в)). В последнем случае точку
разрыва первого рода называютточкой
устранимого разрыва.
В точке разрыва
второго родахотя бы один из односторонних
пределов равен бесконечности или не
существует (как на рисунке 2.10 (а), где
односторонние пределы равны бесконечности).
Непрерывность функции
в точке можно определить и по-другому.
Функция у = f(х)
называется непрерывной в точке х0,
если она определена в эnой
точке и бесконечно малому приращению
аргумента соответствует бесконечно
малое приращение функции:![]() .
.
Под приращением функции
здесь будем понимать разность между
значением функции при значении аргумента,
увеличенном на приращение x,
и ее значением в точкеx0:y=f(x0+x) -f(x0)
(рисунок 2.11).
Можно доказать
эквивалентность этих двух определений
непрерывности.

Рисунок 2.11 –
Приращение аргумента и приращение
функции
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Предел функции
В ряде разделов нашего справочника, где требуется применение понятия предела функции, встречаются несколько ситуаций в зависимости от того, куда стремится аргумент функции x , и того, куда при этом стремится значение функции. Определения предела функции для этих случаев удобно представить в форме таблицы. Однако таблица, описывающая все возможные случаи, должна содержать 24 строки и является слишком громоздкой. Для удобства читателей мы привели в таблице только те определения предела функции, которые использованы в нашем справочнике.
| Название | Обозначение | Определение |
Предел функции f (x) при x, стремящемся к числу a, равен числу A | Число A называют пределом функции f (x) при x, стремящемся к числу a, если для любого положительного числа ε найдется такое положительное число δ , что при всех , удовлетворяющих неравенству | x – a | < δ , будет выполняться неравенство | f (x) – A | < ε . | |
f (x) → A при x → a | ||
Предел функции f (x) при x, стремящемся к , равен числу A | Число A называют пределом функции f (x) при x , стремящемся к, если для любого положительного числа ε найдется такое положительное число С, что при всех x, удовлетворяющих неравенству x > C , будет выполняться неравенство | f (x) – A | < ε . | |
f (x) → A при | ||
Предел функции f (x) при x, стремящемся к , равен числу A | Число A называют пределом функции f (x) при x , стремящемся к, если для любого положительного числа ε найдется такое отрицательное число С, что при всех x, удовлетворяющих неравенству x < C , будет выполняться неравенство | f (x) – A | < ε . | |
f (x) → A при | ||
Предел функции f (x) при x, стремящемся к , равен числу A | Число A называют пределом функции f (x) при x , стремящемся к, если для любого положительного числа ε найдется такое положительное число С, что при всех x, удовлетворяющих неравенству | x | > C , будет выполняться неравенство | f (x) – A | < ε . | |
f (x) → A при x → | ||
Предел функции f (x) при x, стремящемся к , равен | Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое положительное число С, что при всех x, удовлетворяющих неравенству | x | > C , будет выполняться неравенство | f (x)| > D . | |
f (x) → при x → | ||
Предел функции f (x) при x, стремящемся к , равен | Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое положительное число С, что при всех x, удовлетворяющих неравенству x > C , будет выполняться неравенство | f (x)| > D . | |
f (x) → при | ||
Предел функции f (x) при x, стремящемся к , равен | Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое отрицательное число С, что при всех x, удовлетворяющих неравенству x < C , будет выполняться неравенство | f (x)| > D . | |
f (x) → при | ||
Предел функции f (x) при x, стремящемся к числу a слева, равен Замечание. Когда говорят, что x стремится к a слева, то это означает, что при определении предела функции рассматриваются только те значения x , которые меньше a . | Функция f (x) стремится к , при x, стремящемся к числу a слева, если для любого положительного числа С найдется такое положительное число δ что при всех x, удовлетворяющих неравенству a – δ < x < a , будет выполняться неравенство | f (x)| > C . | |
f (x) → при x → a – 0 | ||
Предел функции f (x) при x, стремящемся к числу a справа, равен Замечание. Когда говорят, что x стремится к a справа, то это означает, что при определении предела функции рассматриваются только те значения x , которые больше a . | Функция f (x) стремится к , при x , стремящемся к числу a справа, если для любого положительного числа С, найдется такое положительное число δ что при всех x, удовлетворяющих неравенству a < x < a + δ , будет выполняться неравенство | f (x)| > C . | |
f (x) → при x → a + 0 |
Название: Предел функции f (x) при x, стремящемся к числу a, равен числу A Обозначения: или f (x) → A при x → a Определение: Число A называют пределом функции f (x) при x, стремящемся к числу a, если для любого положительного числа ε найдется такое положительное число δ , что при всех , удовлетворяющих неравенству | x – a | < δ , будет выполняться неравенство | f (x) – A | < ε . |
Название: Предел функции f (x) при x, стремящемся к , равен числу A Обозначения: или f (x) → A при Определение: Число A называют пределом функции f (x) при x , стремящемся к , если для любого положительного числа ε найдется такое положительное число С, что при всех x, удовлетворяющих неравенству x > C , будет выполняться неравенство | f (x) – A | < ε . |
Название: Предел функции f (x) при x, стремящемся к , равен числу A Обозначения: или f (x) → A при Определение: Число A называют пределом функции f (x) при x , стремящемся к , если для любого положительного числа ε найдется такое отрицательное число С, что при всех x, удовлетворяющих неравенству x < C , будет выполняться неравенство | f (x) – A | < ε . |
Название: Предел функции f (x) при x, стремящемся к , равен числу A Обозначения: или f (x) → A при x → Определение: Число A называют пределом функции f (x) при x , стремящемся к, если для любого положительного числа ε найдется такое положительное число С, что при всех x, удовлетворяющих неравенству | x | > C , будет выполняться неравенство | f (x) – A | < ε . |
Название: Предел функции f (x) при x, стремящемся к , равен Обозначения: или f (x) → при x → Определение: Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое положительное число С, что при всех x, удовлетворяющих неравенству | x | > C , будет выполняться неравенство | f (x)| > D . |
Название: Предел функции f (x) при x, стремящемся к , равен Обозначения: или f (x) → при Определение: Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое положительное число С, что при всех x, удовлетворяющих неравенству x > C , будет выполняться неравенство | f (x)| > D . |
Название: Предел функции f (x) при x, стремящемся к , равен Обозначения: или f (x) → при Определение: Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое отрицательное число С, что при всех x, удовлетворяющих неравенству x < C , будет выполняться неравенство | f (x)| > D . |
Название: Предел функции f (x) при x, стремящемся к числу a слева, равен Замечание. Когда говорят, что x стремится к a слева, то это означает, что при определении предела функции рассматриваются только те значения x , которые меньше a . Обозначения: или f (x) → при x → a – 0 . Определение: Функция f (x) стремится к , при x, стремящемся к числу a слева, если для любого положительного числа С найдется такое положительное число δ что при всех x, удовлетворяющих неравенству a – δ < x < a , будет выполняться неравенство | f (x)| > C . |
Название: Предел функции f (x) при x, стремящемся к числу a справа, равен Замечание. Когда говорят, что x стремится к a справа, то это означает, что при определении предела функции рассматриваются только те значения x , которые больше a . Обозначения: или f (x) → при x → a + 0 . Определение: Функция f (x) стремится к , при x , стремящемся к числу a справа, если для любого положительного числа С, найдется такое положительное число δ что при всех x, удовлетворяющих неравенству a < x < a + δ , будет выполняться неравенство | f (x)| > C . |
Свойства пределов функций
Если у функций f (x) и g (x) при x , стремящемся к a , существуют пределы
и ,
где A и B – некоторые числа, то при x , стремящемся к a , существуют также и пределы суммы, разности и произведения этих функций, причем
Если, кроме того, выполнено условие
то при x , стремящемся к a , существует предел дроби
причем
Для любой непрерывной функции F (x) справедливо равенство
Раскрытие неопределенностей типа
Определение 1 . Если при нахождении предела дроби выясняется, что и числитель дроби, и знаменатель дроби стремятся к стремятся к, то вычисление такого предела называют раскрытием неопределенности типа .
Часто неопределенность типа удается раскрыть, если и в числителе дроби, и в знаменателе дроби вынести за скобки «самое большое» слагаемое. Например, в случае, когда в числителе и в знаменале дроби стоят многочлены, «самым большим» слагаемым будет член с наивысшей степенью.
Пример 1. Найти предел функции предел функции
Решение. Вынесем за скобки «самое большое» слагаемое в каждой из скобок числителя и знаменателя дроби и, используя свойства пределов функций, получим
Ответ.
Пример 2. Найти предел функции предел функции
Решение. Преобразуем выражение, стоящее под знаком предела, к более удобному виду:
Далее, используя свойства пределов функций, находим
Ответ. 3 .
Раскрытие неопределенностей типа
Определение 2 . Если при нахождении предела дроби выясняется, что пределы числителя и знаменателя дроби равны 0 , то вычисление такого предела называют раскрытием неопределенности .
В алгебраических дробях неопределенность при x → a раскрывается при помощи разложения на множители числителя и знаменателя дроби с последующим сокращением на соответствующую степень множителя (x – a) .
Пример 3. Найти предел функции
Решение. Поскольку и числитель, и знаменатель дроби стремятся к 0 при x → – 2 , то для того, чтобы раскрыть неопределенность типа , разложим числитель и знаменатель дроби на множители. С этой целью в числителе применим формулу сокращенного умножения «сумма кубов», а в знаменателе – разложение квадратного трехчлена на множители, а затем сократим дробь на (x + 2) :
Теперь предел знаменателя дроби равен – 11 , и, воспользовавшись свойствами пределов функций, получаем
Ответ.
Пример 4. Найти предел функции
Решение. В этом примере также возникает неопределенность типа .
К сожалению, из-за большого размера формул для расчета подробные вычисления на Вашем мобильном устройстве не видны. Их можно посмотреть только на устройствах с разрешением экрана по ширине не менее 768 пикселей (например, на стационарных компьютерах, ноутбуках и некоторых планшетах).
Указания к решению примера. Поскольку знаменатель дроби является разностью двух квадратных корней, каждый из которых стремится к одному и тому же числу 5 при x → 5 , то сначала необходимо домножить и числитель, и знаменатель дроби на сумму этих квадратных корней и применить формулу сокращенного уножения «разность квадратов». Затем, разложив квадратный трехчлен 4x2 – 9x – 55 на множители, сократить числитель и знаменатель на (x – 5) .
После этого, воспользовавшись свойствами пределов функций, получить ответ.
На Вашем мобильном устройстве отображается только результат описанных операций.
Ответ.
Первый замечательный предел
В пределах, содержащих тригонометрические функции, неопределенность раскрывается с помощью первого замечательного предела
Пример 5. Найти предел функции
Решение. Числитель и знаменатель дроби стремятся к 0 при x → 0 , поэтому для того, чтобы раскрыть неопределенность типа , разложим числитель и знаменатель дроби на множители. С этой целью в числителе вынесем за скобки x2, а в знаменателе воспользуемся формулой «разность косинусов»:
Теперь, воспользовавшись первым замечательным пределом и свойствами пределов функций, получаем
Ответ.
Пример 6. Найти предел функции
Решение. Чтобы вычислить данный предел, перейдем от переменной x к новой переменной z по формуле
.
Поскольку
,
то предел можно преобразовать к виду
Применяя формулы приведения и формулу для косинуса двойного угла, получаем
Теперь, воспользовавшись первым замечательным пределом и свойствами пределов функций, получаем
Ответ.
Раскрытие неопределенности типа . Второй замечательный предел
Определение 3. Если при нахождении предела степени некоторого выражения выясняется, что предел основания степени равен 1, а предел показателя степени равен , то вычисление такого предела называют раскрытием неопределенности .
Неопределенность раскрывается с помощью второго замечательного предела:
| (1) |
Если взять натуральный логарифм от обеих частей формулы (1), то второй замечательный предел примет вид:
| (2) |
Пример 7. Найти предел функции предел функции
Решение. Рассмотрим функцию
и, взяв от нее натуральный логарифм, найдем сначала предел функции y = ln f (x) при x →. Применяя свойства логарифмов, получаем
Преобразуем выражение, стоящее под знаком логарифма к виду, удобному для применения второго замечательного предела,
и заметим, что
В пределе
и числитель, и знаменатель дроби стремятся к стремятся к, поэтому для раскрытия неопределенности вынесем за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в знаменателе дроби и, используя свойства пределов функций, получим
Следовательно,
Таким образом,
Ответ.
Пример 8. Найти предел функции
Решение. Рассмотрим функцию
и, взяв от нее натуральный логарифм, найдем сначала предел функции y = ln f (x) при x → – 6 . Применяя свойства логарифмов, получаем
Чтобы вычислить предел функции y = ln f (x) при x → – 6 , перейдем от переменной x к новой переменной z по формуле
x = – 6 + z .
Поскольку
то предел (3) можно преобразовать к виду, с помощью формулы (3), получаем
Воспользовавшись вторым замечательным пределом в виде (2) и свойствами пределов функций, получаем
Следовательно,
Ответ.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
