Какими свойствами обладают нулевые коллинеарные векторы
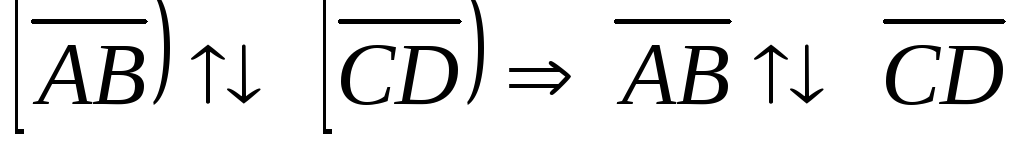
В статье ниже рассмотрим условия, при которых векторы считаются коллинеарными, а также разберем тему на конкретных примерах. И, прежде чем приступить к обсуждению, напомним некоторые определения.
Определение 1
Коллинеарные векторы – ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому.
Данное определение дает возможность убедиться в коллинеарности векторов в их геометрическом отображении, однако точность такого способа может иметь погрешности, например, в зависимости, от качества самого чертежа. Поэтому обратимся к алгебраическому толкованию: сформируем условие, которое будет явным признаком коллинеарности.
Согласно схемам операций над векторами умножение вектора на некоторое заданное число приводит к соответствующему сжатию или растяжению вектора при сохранении или смене направления. Тогда вектор b→=λ·a→ коллинеарен вектору a→ , где λ – некоторое действительное число. Справедливым будет и обратное утверждение: если вектор b→ коллинеарен вектору a→, его можно представить в виде λ·a→. Это является необходимым и достаточным условием коллинеарности двух ненулевых векторов.
Определение 2
Для коллинеарности двух векторов необходимо и достаточно, чтобы они были связаны равенствами: b→=λ·a→ или a→=μ·b→, μ∈R
Координатная форма условия коллинеарности векторов
Исходные данные: вектор a→ задан в некоторой прямоугольной системе координат на плоскости и имеет координаты (ax, ay), тогда, согласно полученному выше условию, вектор b→=λ·a→ имеет координаты (λ·ax, λ·ay).
По аналогии: если вектор a→ задан в трехмерном пространстве, то он будет представлен в виде координат a=(ax, ay, az) , а вектор b→=λ·a→ имеет координаты (λ·ax, λ·ay, λ·az). Из полученных утверждений следуют условия коллинеарности двух векторов в координатном толковании.
Определение 3
- Для коллинеарности двух ненулевых векторов на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями: bx=λ·axby=λ·ay или ax=μ·bxay=μ·by
- Для коллинеарности двух ненулевых векторов в пространстве необходимо и достаточно, чтобы их координаты были связаны соотношениями:bx=λ·axby=λ·ay bz=λ·azили ax=μ·bxay=μ·by az=μ·bz
Мы можем также получить еще одно условие коллинеарности векторов, опираясь на понятие их произведения.
Если ненулевые векторы a→=(ax, ay, az) и b→=(bx, by, bz) коллинеарны, то согласно векторному определению произведения a→×b→=0→. И это также соответствует равенству: i→j→k→axayazbxbybz=0→, что, в свою очередь, возможно только тогда, когда заданные векторы связаны соотношениями b→=λ·a→ и a→=μ·b→ , где μ — произвольное действительное число (на основании теоремы о ранге матрицы), что указывает на факт коллинеарности векторов.
Определение 4
Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
Рассмотрим применение условия коллинеарности на конкретных примерах.
Пример 1
Исходные данные: векторы a→=(3-22, 1) и b→=(12+1, 2+1) . Необходимо определить, коллинеарны ли они.
Решение
Выполним задачу, опираясь на условие коллинеарности векторов на плоскости в координатах: bx=λ·axby=λ·ay Подставив заданные значения координат, получим: bx=λ·ax⇔12+1=λ·(3-22)⇒λ=1(2+1)·(3-22)=132-4+3-22=12-1by=λ·ay⇔2+1=12-1·1⇔(2+1)·(2-1)=1 ⇔1≡1
Т.е. b→=12-1·a→, следовательно, заданные векторы коллинеарны.
Ответ: заданные векторы коллинеарны.
Пример 2
Исходные данные: векторы a→=(1, 0, -2) и b→=(-3, 0, 6) . Необходимо убедиться в их коллинеарности.
Решение
Т.к. bx=λ·axby=λ·ay bz=λ·az⇔-3=-3·10=-3·06=-3·(-2) , то верным будет равенство: b→=-3·a→ , что является необходимым и достаточным условием коллинеарности. Таким образом, заданные векторы коллинеарны.
Найдем также векторное произведение заданных векторов и убедимся, что оно равно нулевому вектору: a→×b→=i→j→k→axayazbxbybz=i→j→k→10-2-306=i→·0·6+j→·(-2)·(-3)+k→·1·0-k→·0·(-3)-j→·1·6-i→·(-2)·0=0→Ответ: заданные векторы коллинеарны.
Пример 3
Исходные данные: векторы a→=(2, 7) и b→=(p, 3) . Необходимо определить, при каком значении pзаданные векторы будут коллинеарны.
Решение
Согласно выведенному выше условию, векторы коллинеарны, если
b→=λ·a→⇔bx=λ·axby=λ·ay⇔p=λ·23=λ·7
тогда λ=37, а p=λ·2⇔p=67 .
Ответ: при p=67 заданные векторы коллинеарны.
Также распространены задачи на нахождения вектора, коллинеарного заданному. Решаются они без затруднений, основываясь на условии коллинеарности: : достаточным будет взять произвольное действительное число λ и определить вектор, коллинеарный данному.
Пример 4
Исходные данные: вектор a→=(2, -6) . Необходимо найти любой ненулевой вектор, коллинеарный заданному.
Решение
Ответом может послужить, например, 12·a→=(1, -3) или вектор 3·a→=(6, -18) .
Ответ: вектор, коллинеарный заданному имеет координаты (1, -3).
Пример 5
Исходные данные: вектор a→=(3, 4, -5) . Необходимо определить координаты вектора единичной длины, коллинеарного заданному.
Решение
Вычислим длину заданного вектора по его координатам: a→=ax2+bx2+cx2=32+42+(-5)2=52 Разделим каждую из заданных координат на полученную длину и получим единичный вектор, коллинеарный данному: 1a→·a→=(352, 452,- 12)
Ответ: (352, 452,- 12)
1. Нулевой вектор
коллинеарен любому вектору: Если
![]()
(или
![]() ),
),
то
![]()
(или
![]() ).
).
2. Нулевой вектор
одинаково направлен с любым вектором,
![]() .
.
3. Любые два
коллинеарных вектора можно отложить
на одной прямой.
Достаточно отложить
векторы от одной точки.
4. На прямой можно
указать всего два направления,
следовательно, два вектора, отложенных
на ней могут иметь либо одно и то же
направление, либо противоположное.
Определение 4.
Векторы
![]()
и
![]()
называются противоположными.
Рассмотрим вектор
![]() .
.
Отложим его от точки А.
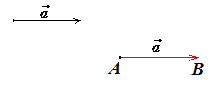
Для вектора
![]() =
=![]()
противоположным называется вектор
![]() ,
,
![]() =–
=–![]() .
.
Вектор, противоположный
![]() ,
,
это вектор
![]() ,
,
т.е.
![]() =–(–
=–(–![]() ).
).
Для нулевого
вектора
![]()
противоположным является вектор
![]() ,
,
или
![]() =–
=–![]() .
.
Определение 5.
Ненулевые векторы
![]()
и
![]()
называются одинаково
направленными
(сонаправленными), если лучи АВ
и CD
одинаково направлены, обозначается
символом
![]() :
:
![]() .
.
Ненулевые векторы
![]()
и
![]()
называются противоположно
направленными,
если лучи АВ
и CD
противоположно направлены, обозначается
символом
![]() :
:
![]() .
.
3. Абсолютная величина вектора
Определение 6.
Модулем
(длиной, абсолютной величиной)
вектора
![]()
называется длина отрезка АВ,
обозначается
![]() ,
,
![]() или
или
АВ.
Длина нулевого
вектора равна нулю:
![]() .
.
Определение 7.
Вектор, абсолютная
величина которого равна единице,
называется единичным.
Единичный вектор
обозначается
![]() ,
,
![]() .
.
4. Равенство векторов
Определение 8.
Два вектора
![]()
и
![]()
называются равными,
если выполнены следующие условия:
1) они имеют
одинаковое направление,
![]()
![]()
![]() ;
;
2) абсолютные
величины их равны, |![]() |=|
|=|![]() |.
|.
Из определения
следует, что два нулевых вектора всегда
равны.
Равенство векторов
обладает свойствами, аналогичными
свойствам равенства чисел.
Свойства равенства
векторов:
1. Рефлексивность:
каждый вектор равен самому себе
![]() ;
;
2. Симметричность:
![]() .
.
3. Транзитивность:
![]() .
.
Равенство векторов
является отношением эквивалентности.
5. Линейные операции над векторами
Линейными операциями
над векторами называются сложение
векторов и умножение вектора на
действительное число.
5.1. Сложение векторов
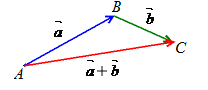
Определение 9
(Правило треугольника).
Суммой
векторов
![]()
и
![]() ,
,
отложенных последовательно, называется
вектор
![]() ,
,
начало которого совпадает с началом
первого слагаемого вектора, а конец –
с концом второго.
![]() ,
,
![]() (7.1)
(7.1)
Сумма векторов
существует и определена однозначно.
Свойства сложения:
![]()
1. | С=В |
|
|
2. | С=В, |
|
|
3. | С=А |
|
|
4. | Коммутативность |
| |
5. | Ассоциативность |
|
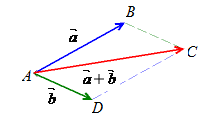
Определение 10
(Правило параллелограмма).
Суммой
векторов
![]()
и
![]() ,
,
отложенных от общего начала, называется
вектор
![]() ,
,
задаваемый диагональю построенного на
них, как на сторонах, параллелограмма,
исходящей из их общего начала. Начало
вектора суммы совпадает с началом
слагаемых векторов, а конец – с
противоположным концом диагонали
параллелограмма.
Сложение двух
скользящих
векторов
определено лишь в случае, когда прямые,
на которых они расположены, пересекаются.
Тогда каждый из векторов переносится
вдоль своей прямой в точку пересечения
этих прямых, после чего сложение
осуществляется по правилу параллелограмма.
Сложение двух
связных
(фиксированных) векторов
определено лишь в случае, когда они
имеют общее начало. Их сложение в этом
случае осуществляется по правилу
параллелограмма.
Определение 11
(Правило многоугольника).
Суммой
nвекторов
![]() ,
,
отложенных последовательно, называется
вектор, начало которого совпадает с
началом первого слагаемого вектора, а
конец – с концом последнего слагаемого
вектора.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Условия коллинеарности векторов
Два вектора будут коллинеарны при выполнении любого из этих условий:
Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что
a = n · b
Условия коллинеарности векторов 2. Два вектора коллинеарны, если отношения их координат равны.
N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.
Условия коллинеарности векторов 3. Два вектора коллинеарны, если их векторное произведение равно нулевому вектору.
N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Доказательство третего условия коллинеарности
Пусть есть два коллинеарные вектора a = {ax; ay; az} и b = {nax; nay; naz}. Найдем их векторное произведение
a × b =
ijkaxayazbxbybz
= i (aybz — azby) — j (axbz — azbx) + k (axby — aybx) =
= i (aynaz — aznay) — j (axnaz — aznax) + k (axnay — aynax) = 0i + 0j + 0k = 0
Примеры задач на коллинеарность векторов
Примеры задач на коллинеарность векторов на плоскости
Пример 1. Какие из векторов a = {1; 2}, b = {4; 8}, c = {5; 9} коллинеарны?
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:
Значит:
| Вектора a и b коллинеарны т.к. | 1 | = | 2 | . |
| 4 | 8 |
| Вектора a и с не коллинеарны т.к. | 1 | ≠ | 2 | . |
| 5 | 9 |
| Вектора с и b не коллинеарны т.к. | 5 | ≠ | 9 | . |
| 4 | 8 |
Пример 2. Доказать что вектора a = {0; 3} и b = {0; 6} коллинеарны.
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
b = na.
Для этого найдем ненулевой компонент вектора a в данном случае это ay. Если вектора колинеарны то
Найдем значение na:
na = {2 · 0; 2 · 3} = {0; 6}
Так как b = na, то вектора a и b коллинеарны.
Пример 3. найти значение параметра n при котором вектора a = {3; 2} и b = {9; n} коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
Значит:
Решим это уравнение:
Ответ: вектора a и b коллинеарны при n = 6.
Примеры задач на коллинеарность векторов в пространстве
Пример 4. Какие из векторов a = {1; 2; 3}, b = {4; 8; 12}, c = {5; 10; 12} коллинеарны?
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:
| ax | = | ay | = | az | . |
| bx | by | bz |
Значит:
Вектора a и b коллинеарны т.к.
14 = 28 = 312
Вектора a и с не коллинеарны т.к.
15 = 210 ≠ 312
Вектора с и b не коллинеарны т.к.
54 = 108 ≠ 1212
Пример 5. Доказать что вектора a = {0; 3; 1} и b = {0; 6; 2} коллинеарны.
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
b = na.
Для этого найдем ненулевой компонент вектора a в данном случае это ay. Если вектора колинеарны то
Найдем значение na:
na = {2 · 0; 2 · 3; 2 · 1} = {0; 6; 2}
Так как b = na, то вектора a и b коллинеарны.
Пример 6. найти значение параметров n и m при которых вектора a = {3; 2; m} и b = {9; n; 12} коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | = | az | . |
| bx | by | bz |
Значит:
Из этого соотношения получим два уравнения:
Решим эти уравнения:
Ответ: вектора a и b коллинеарны при n = 6 и m = 4.
В данной статье мы расскажем:
- что такое коллинеарные векторы;
- какие существуют условия коллинеарности векторов;
- какие существуют свойства коллинеарных векторов;
- что такое линейная зависимость коллинеарных векторов.
Коллинеарные векторы
Определение 1
Коллинеарные векторы — это векторы, которые являются параллелями одной прямой или лежат на одной прямой.
Пример 1
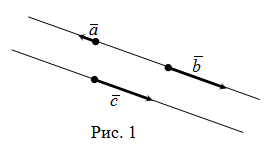
Условия коллинеарности векторов
Два векторы являются коллинеарными, если выполняется любое из следующих условий:
- условие 1. Векторы a и b коллинеарны при наличии такого числа λ, что a=λb;
- условие 2. Векторы a и b коллинеарны при равном отношении координат:
a=(a1; a2), b=(b1; b2)⇒a∥b⇔a1b1=a2b2
- условие 3. Векторы aи b коллинеарны при условии равенства векторного произведения и нулевого вектора:
a∥b⇔a, b=0
Замечание 1
Условие 2 неприменимо, если одна из координат вектора равна нулю.
Замечание 2
Условие 3 применимо только к тем векторам, которые заданы в пространстве.
Примеры задач на исследование коллинеарности векторов
Пример 1
Исследуем векторы а=(1; 3) и b=(2; 1) на коллинеарность.
Как решить?
В данном случае необходимо воспользоваться 2-м условием коллинеарности. Для заданных векторов оно выглядит так:
12=-31
Равенство неверное. Отсюда можно сделать вывод, что векторы a и b неколлинеарны.
Ответ: a | | b
Пример 2
Какое значение m вектора a=(1; 2) и b=(-1; m) необходимо для коллинеарности векторов?
Как решить?
Используя второе условие коллинераности, векторы будут коллинеарными, если их координаты будут пропорциональными:
1-1=2m
Отсюда видно, что m=-2.
Ответ: m=-2.
Критерии линейной зависимости и линейной независимости систем векторов
Теорема
Система векторов векторного пространства линейно зависима только в том случае, когда один из векторов системы можно выразить через остальные векторы данной системы.
Доказательство
Пусть система e1, e2, …, en является линейно зависимой. Запишем линейную комбинацию этой системы равную нулевому вектору:
a1e1+a2e2+…+anen=0
в которой хотя бы один из коэффициентов комбинации не равен нулю.
Пусть ak≠0 k∈1, 2, …, n.
Делим обе части равенства на ненулевой коэффициент:
ak-1(ak-1a1)e1+(ak-1ak)ek+…+(ak-1an)en=0
Обозначим:
-ak-1am, где m∈1, 2,…, k-1, k+1, n
В таком случае:
β1e1+…+βk-1ek-1+βk+1ek+1+…+βnen=0
или ek=(-β1)e1+…+(-βk-1)ek-1+(-βk+1)ek+1+…+(-βn)en
Отсюда следует, что один из векторов системы выражается через все остальные векторы системы. Что и требовалось доказать (ч.т.д.).
Достаточность
Пусть один из векторов можно линейно выразить через все остальные векторы системы:
ek=γ1e1+…+γk-1ek-1+γk+1ek+1+…+γnen
Переносим вектор ek в правую часть этого равенства:
0=γ1e1+…+γk-1ek-1-ek+γk+1ek+1+…+γnen
Поскольку коэффициент вектора ek равен -1≠0, у нас получается нетривиальное представление нуля системой векторов e1, e2, …, en, а это, в свою очередь, означает, что данная система векторов линейно зависима. Что и требовалось доказать (ч.т.д.).
Следствие:
- Система векторов является линейно независимой, когда ни один из ее векторов нельзя выразить через все остальные векторы системы.
- Система векторов, которая содержит нулевой вектор или два равных вектора, линейно зависима.
Свойства линейно зависимых векторов
- Для 2-х и 3-х мерных векторов выполняется условие: два линейно зависимых вектора — коллинеарны. Два коллинеарных вектора — линейно зависимы.
- Для 3-х мерных векторов выполняется условие: три линейно зависимые вектора — компланарны. (3 компланарных вектора — линейно зависимы).
- Для n-мерных векторов выполняется условие: n+1 вектор всегда линейно зависимы.
Примеры решения задач на линейную зависимость или линейную независимость векторов
Пример 3
Проверим векторы a=3, 4, 5, b=-3, 0, 5, c=4, 4, 4, d=3, 4, 0 на линейную независимость.
Решение. Векторы являются линейно зависимыми, поскольку размерность векторов меньше количества векторов.
Пример 4
Проверим векторы a=1, 1, 1, b=1, 2, 0, c=0, -1, 1 на линейную независимость.
Решение. Находим значения коэффициентов, при которых линейная комбинация будет равняться нулевому вектору:
x1a+x2b+x3c1=0
Записываем векторное уравнение в виде линейного:
x1+x2=0x1+2×2-x3=0x1+x3=0
Решаем эту систему при помощи метода Гаусса:
110|012-1|0101|0~
Из 2-ой строки вычитаем 1-ю, из 3-ей — 1-ю:
~110|01-12-1-1-0|0-01-10-11-0|0-0~110|001-1|00-11|0~
Из 1-й строки вычитаем 2-ю, к 3-ей прибавляем 2-ю:
~1-01-10-(-1)|0-001-1|00+0-1+11+(-1)|0+0~010|101-1|0000|0
Из решения следует, что у системы множество решений. Это значит, что существует ненулевая комбинация значения таких чисел x1, x2, x3, при которых линейная комбинация a, b, c равняется нулевому вектору. Следовательно, векторы a, b, c являются линейно зависимыми.
10 класс
Материалы к зачетной работе по теме
«РџРµСЂРїРµРЅРґРёРєСѓР»СЏСЂРЅРѕСЃС‚СЊ прямых Рё плоскостей. Векторы РІ пространстве»
Параллельный перенос Введём на плоскости декартовы координаты xОу. Преобразование некоторой фигуры F, при котором произвольная ее точка А (х;у) переходит в другую точку А (х+a; y+b), где а и b постоянные, называется параллельным переносом; | |
Величины, которые характеризуются, РЅРµ только числом, РЅРѕ еще Рё направлением, называются векторными величинами или просто векторами. Векторами являются, например, скорость, ускорение, сила. Геометрически векторы изображаются направленными отрезками. Если начало вектора — точка Рђ, Р° его конец — точка Р’, то вектор обозначается или . РћС‚ любой точки можно отложить вектор, равный данному, Рё притом только РѕРґРёРЅ, используя параллельный перенос. Нулевой вектор — точка РІ пространстве. Начало Рё конец нулевого вектора совпадают, Рё РѕРЅ РЅРµ имеет длины Рё направления. Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютная величина вектора . | векторы |
Два вектора называются равными, если они совмещаются параллельным переносом. | |
коллинеарные векторы: | |
| |
Правило треугольника | |
|
|
Правило параллелограмма Если векторы и неколлинеарны, их можно отложить от одной точки, достроив затем параллелограмм. |
Свойства сложения векторов
Для любых векторов заданных в пространстве, справедливы равенства
Переместительный закон | |
Сочетательный закон |
Свойства умножения вектора на число
Для любых векторов и и любых чисел k, m справедливы равенства:
Сочетательный закон | |
Первый распределительный закон | |
Второй распределительный закон |
Компланарные векторы
Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости. Любые два вектора компланарны.
Три вектора, среди которых имеются два коллинеарных, также компланарны.
Три произвольных вектора могут быть компланарными (лежать в одной плоскости) или некомпланарными
(не лежать в одной плоскости).
Признак компланарности трех векторов
Если вектор можно разложить РїРѕ векторам Рё , С‚.Рµ. представить РІ РІРёРґРµ , РіРґРµ С… Рё Сѓ — некоторые числа, то векторы , Рё компланарны. |
Правило параллелепипеда Сумма трех некомпланарных векторов равна вектору, изображаемому направленной диагональю параллелепипеда, построенному на этих векторах. |
Угол между двумя векторами
Углом между двумя направлениями в пространстве называется величина наименьшего угла между любыми лучами
этих направлений с общим началом.
Угол между лучами обозначается . По определению угол между двумя направлениями находится
в промежутке [0°; 180°].
Углом между двумя ненулевыми векторами называется угол между направлениями этих векторов. |
Перпендикулярные векторы (или ортогональные) | Коллинеарные векторы | |
Сонаправленные | Противоположно направленные | |
90В° | 0В° | 180В° |
Базис вектора. Разложение вектора на плоскости по двум некомпланарным векторам Теорема: Любой вектор на плоскости может быть представлен, и притом единственным образом, в виде двух любых неколлинеарных векторов и : Числа x и y называются координатами вектора. Векторы и называются базисом вектора на плоскости. |
Разложение вектора по трем некомпланарным векторам
Базисом пространства называют любые три некомпланарных вектора, взятые в определенном порядке
Теорема: Любой вектор на плоскости может быть представлен, и притом единственным образом, в виде линейной комбинации трех любых неколлинеарных векторов , и : Числа x, y и z называются координатами вектора в данном базисе. В этом случае пишут: |
Действия над векторами, заданными своими координатами
Сложение | Вычитание | Умножение |
При сложении векторов их соответстветственные координаты | При вычитании векторов их соответстветственные координаты | При умножении вектора на число все его координаты умножаются на это число. |
