Какими свойствами обладают неоднородные линии

Проведённый выше анализ процессов и явлений в симметричных и коаксиальных цепях предполагал однородность линии. Однородная линия имеет постоянные электрические характеристики на всём протяжении, она нагружена на концах сопротивлениями, равными волновому . В этом случае отраженных электромагнитных волн нет и вся передаваемая энергия полностью поглощается приёмником, электрические процессы в линии точно описываются уравнениями (3.1, 3.2), а затухание линии определяется её собственным затуханием.
При изготовлении кабелей вследствие не совершенства технологии возникают различные дефекты: деформации изоляции, проводников, отклонения диаметров проводников и толщины изоляции от номинальных значений, эллиптичность проводников в коаксиальной паре, их несоосность и др. Вследствие этого кабель становится неоднородным по длине, изменяются его параметры, линия становится неоднородной. Однородность линии определяется постоянством волнового сопротивления по длине линии. Мерой неоднородности линии является коэффициент отражения p в месте сосредоточенной неоднородности (рис. 5.6).
Рисунок 5.6 – Схема однородной (а) и неоднородной (б) линии
. (5.31)
В неоднородной линии появляются отраженные волны, которые искажают характеристику собственного волнового сопротивления линии. Теперь линия характеризуется входным сопротивлением, характер которого приведен на рис. 5.7.
Рисунок 5.7 – Частотная зависимость входного сопротивления цепи
Изменение входного сопротивления цепи на её концах приводит к несогласованности на концах линии и к появлению концевых отражений с коэффициентом отражения
,
где — входное сопротивление линии.
Дальность связи по неоднородной линии будет определяться не собственным затуханием линии , а рабочем затуханием
, (5.32)
где и – коэффициенты отражения на стыках “генератор–кабель” и “приёмник–кабель”.
; .
Рабочее затухание — более общий параметр, т.к. кроме собственного затухания кабеля , учитывает также влияние несогласованности на стыках кабеля с нагрузкой.
В линиях неоднородных по длине различают внутренние неоднородности — в пределах строительной длины кабеля, и стыковые – обусловленные разбросом конструктивных, а следовательно, и электрических параметров.
Стыковые неоднородности, как правило, превышает внутренние неоднородности в кабеле сказываются, главным образом, на волновом сопротивлении кабеля, величина которого в месте сосредоточенной неоднородности отличается от номинальной.
Реальный кабель является неоднородной цепью. Электромагнитная волна, распространяясь по такой цепи и встречая на своём пути неоднородность, частично отражается от неё и возвращается к началу линии. При наличии нескольких неоднородных участков при распространении волны возникают многократные частичные отражения, что вызывает увеличение рабочего затухания и искажения характеристик цепи.
Неоднородности в кабеле приводят к появлению в цепи двух дополнительных потоков энергии: обратного (встречного), движущегося к началу цепи (генератору), и попутного, совпадающего с основным потоком. Схема образования встречных и попутных потоков представлена на рис. 5.2.
Рисунок 5.8 – Схема образования встречного и попутного потоков
Попутный поток особенно проявляется на длинных линиях. Попутный поток искажает форму передаваемого сигнала, создаёт помехи. Появление попутного потока отрицательно влияет на передачу телевизионных сигналов,
т. к. в этом случае нарушаются фазовые соотношение в структуре ТВ сигнала.
Величина попутного потока не должна превышать 1% основного. В аналоговых системах передачи попутный лимитируется на участке ОП1 – ОП2 линии, а в цифровых – на длине регенерационного участка.
Для повышения однородности электрических характеристик линии производится группирование строительных длин кабеля. При этом строительные длины располагают так, чтобы величины их волновых сопротивлений нарастали от начала регенерационного (усилительного) участка к его середине. На концах линии прокладываются кабели с номинальным волновым сопротивлением.
Вопросы для самоконтроля
1. Дайте определение однородной и неоднородной линии.
2. Чем характеризуется степень однородности линии?
3. Какие факторы приводят к неоднородности линии?
4. Дайте определение рабочего затухания.
5. Объясните смысл всех слагаемых в 5.1.
6. Как образуются встречный и попутный потоки?
7. Как влияют встречный и попутный потоки на передачу различных сигналов?
8. Какие неоднородности существуют в кабелях?
9. Какие меры применяются для повышения однородности линии?
Рекомендуемые страницы:
В
неоднородной линии отраженные волны
искажают частотную характеристику
собственного волнового сопротивления
кабеля. Подключенный ко входу цепи
измерительный прибор покажет уже не
волновое, а входное
сопротивление
Zвх,
характеризующее новое электрическое
состояние линии. Затухание неоднородной
линии представляет собой суммарную
величину, включающую, кроме собственного
затухания кабеля также затухание за
счет неоднородности электрических
характеристик цепи. Дальность связи по
такой кабельной линии будет обусловливаться
не собственным затуханием линии a
= l,
а ее рабочим
затуханием
ар.
Следует
отметить, что передача электромагнитной
энергии по неоднородным линиям находится
в неблагоприятных условиях и качество
связи по ним может быть совершенно
неудовлетворительным.
Линии
с несогласованными нагрузками по концам.
Входным
сопротивлением такой линии будет
сопротивление, измеренное на входе
линии при любом нагрузочном сопротивлении
на ее конце.
Zвх
= U / I = Zв
th (γl
+ n)
где
n
= 0,51n[(Zв
+ Zl)/(Zв
— Zl)]
= 0,51n(1/р);
р
—
коэффициент отражения.
Если
линия имеет согласованную нагрузку (Zl
= Zв),
то Zвх
= Zв
и коэффициент отражения р
= 0. Для электрически длинной линии при
любой нагрузке на ее конце.
Входное
сопротивление линии можно также выразить
через величину эквивалентного коэффициента
отражения р,
отнесенную к началу линии, в виде
Zвх
= Zв
[(1 + p)/(1
— p)]
≈ Zв
(1 + 2p)
Рабочее
затухание
aр
является затуханием кабельной цепи в
рабочих условиях, т. е. при любых
нагрузочных сопротивлениях (Z
и Zl)
на концах. Оно представляет более общий
параметр, так как кроме собственного
затухания кабеля a
= αl
учитывает также влияние несогласованности
на стыках кабеля (Zв)
с нагрузкой (Z
и Zl).
Рабочее
затухание рассчитывается по формуле
aр
= aсобствен.
+ анач
+ аконец
+ авзаимод.
aр
= αl
+ ln
| (Z
+ Zв)/2√ZZв
| + ln
| (Zl
+ Zв)/2√ZlZв
| + ln
| 1 – p1p2e-2γ
Неоднородности
в кабеле приводят к появлению в цепи
двух дополнительных потоков энергии:
обратного,
состоящего из суммы элементарных
отраженных волн в местах неоднородностей
и движущегося к началу цепи, и попутного,
возникающего по закону двойных отражений
вследствие того, что первоначально
отраженные волны, движущиеся к началу
цепи, встречая места неоднородностей,
частично отражаются и направляются к
концу линии.
12. Оценка искажений импульсных сигналов в двухпроводных линиях связи с потерями
Условие
Хевисайда: если в некоторой цепи L*G=C*R
до искажения будут отсутствовать ( для
реальных кабелей условие не выполняется
).
На
вход подаётся единичный импульс.
При
↑N
↓затухание
отклика
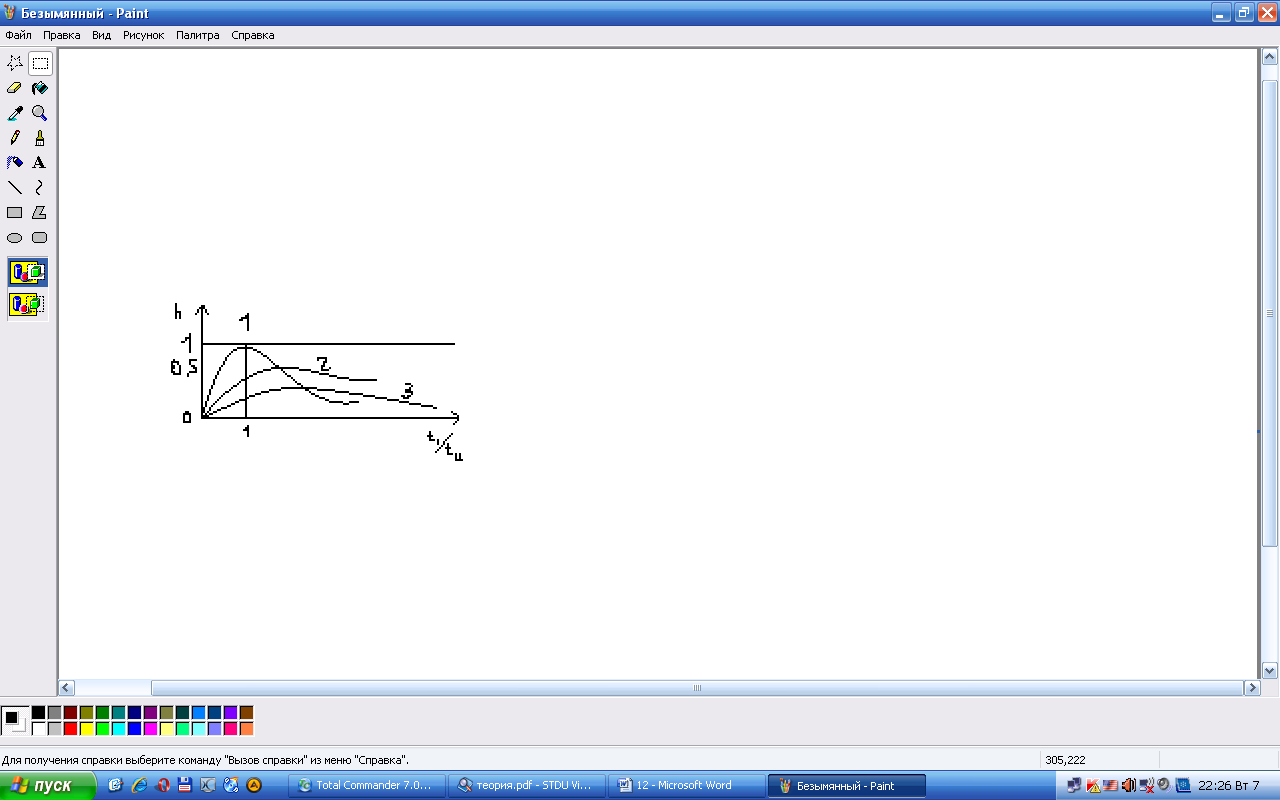
1.
tu/N=200
t1 – текущее время, tu – длительность
импульса
2.
tu/N=20
Параметр N ~ (α*l)2/2
3.
tu/N=2
Форма
искажения импульсных сигналов в
двухпроводных линиях связи с потерями
определяется:
А)
затуханием
Б)
длиной кабельной магистрали
Чем
↑А) и Б) тем ↑ искажение формы сигнала.
Возникает межсимвольная интерференция.
Межсимвольная
интерференция ярко проявляется при
высоких скоростях передачи информации.При
передаче с высокими скоростями –
2400-9600 бит/с и выше, т.е. при удельных
скоростях Бод/Гц и более, наиболее
главными становятся искажения АЧХ и
ФЧХ. Дело в том, что эти искажения вызывают
изменения формы переданных сигналов,
появления «хвостов» которые тянутся
за сигналами переносчиками.
Исследование отраженного сигнала позволяет обнаруживать, определять местоположение и идентифицировать неоднородности в линии передачи, составлять модели неоднородностей.
Возможности обнаружения и определения величины неоднородностей, разделения во времени действия двух неоднородностей определяются длительностью фронта зондирующего сигнала, его амплитудой и отношением сигнал/шум стробоскопического преобразователя, используемого в исследованиях. Для подобных исследований используется метод рефлектометрии (от слова «рефлекс») – измерение реакции объекта на сигнал определенной формы.
Принцип действие рефлектометра аналогичен действию локационной системы с высоким разрешением во времени. При исследованиях неоднородностей линии передачи зондирующий сигнал распространяется по неоднородной линии передачи, рисунок 30.
Рисунок 30. Структурная схема измерений неоднородностей линии передачи.
Коэффициент отражения при последовательном включении однородности в линию определяется величиной комплексного сопротивления:
,
при параллельном включении неоднородностей в линию — величиной проводимости:
Таким образом, для получения отрицательного коэффициента отражения используется параллельное подключение элементов к линии передачи или уменьшение волнового сопротивления линии, для получения положительного коэффициента отражения используется последовательное подключение элементов в линию передачи или увеличение волнового сопротивления линии. Значения коэффициента отражения в частотной области могут быть определены по значению комплексного сопротивления или проводимости элементов, полученному из приведенных выше выражений.
Для определения значения элементов по временной зависимости коэффициента отражения используется зондирование линии стандартными сигналами с известным спектром. Чаще всего используется единичный перепад напряжения.
Для определения величины элементов в воспользуемся известными выражениями, используемыми в импульсной рефлектометрии [3].
Рассмотри параллельное подключение емкости в линию. Операторный коэффициент отражения
При малых значениях емкости, Выражение означает, что во временной области происходит дифференцирование зондирующего сигнала и инверсия.
В результате возникает отраженный сигнал
.
Если зондирующий сигнал имеет линейно нарастающий фронт и амплитуду Е, то
Учитывая, что постоянная времени заряда определим значение емкости по величине отраженного сигнала:
.
Обычно в расчетах используются нормированные значения коэффициента отражения, , далее под U0 будем подразумевать нормированную величину.
Заряд емкости происходит по экспоненциальному закону, поэтому погрешность определения величины емкости возрастает при увеличении U0. При U0 =0,5 погрешность . При больших значениях U0 необходимо определять площадь отраженного сигнала:
.
При последовательном включении в линию передачи индуктивности
Меняется знак коэффициента отражения. Поэтому все полученные формулы справедливы и для индуктивности, с учетом . Величину индуктивности определяем по формуле
При больших коэффициентах отражения
Последовательная емкость в линии передачи:
Происходит заряд емкости с постоянной времени
По известному времени нарастания напряжения на конденсаторе и фронту зондирующего импульса определим время заряда конденсатора , с учетом =2,2 τ0
Аналогичны определения параллельной индуктивности по операторному коэффициенту передачи
:
Сведем наиболее часто используемые схемы корректирующих цепей, формы переходных характеристик и расчетные формулы в таблицу 1.
Таблица 1. Расчетные формулы для определения
неоднородностей в линии передачи.
Рассмотрим пример включения неоднородностей в линию передачи, показанный на рисунке 31.
Рисунок31. Структурная схема неоднородностей линии передачи.
Определим точки подключения реактивных неоднородностей С1, Ll, в линию передачи. Расстояния от входа линии до соответствующих неоднородностей связываются с началом процессов следующим соотношением:
При зондировании этой линии передачи перепадом напряжения с коротким фронтом получим рефлектограмму, приведенную на рисунке 32.
Рис.32. Рефлектограмма неоднородностей в линии передачи
Параллельное подключение конденсатора на время заряда емкости снижает сопротивление на конце первого отрезка линии передачи, в результате отраженный сигнал имеет отрицательный знак. В случае малой емкости, при условии, что постоянная времени заряда , длительность переднего фронта отраженного сигнала равна длительности переднего фронта зондирующего импульса. Длительность заднего фронта в этом случае определяется временем перехода от переднего фронта к вершине зондирующего импульса и для случая малого выброса переднего фронта или монотонного импульса принимается также равным переднему фронту зондирующего сигнала.
Таким образом, длительность отраженного сигнала, при условии малых величин неоднородностей (при ), равна удвоенному переднему фронту. После заряда емкости она на зондирующий сигнал больше не влияет.
Последовательно включенная небольшая индуктивность приводит к кратковременному повышению сопротивления на выходе второй линии передачи. Отраженный сигнал при этом имеет положительный знак. При условии, что постоянная времени изменения тока через индуктивность , длительность отраженного сигнала принимается равной удвоенному фронту.
Изменение волнового сопротивления линии приводит частотно-независимому отражению, а длительность реакции определяется передним фронтом зондирующего импульса и длиной линии передачи с неизменным волновым сопротивлением.
Знак коэффициента отражения при подключении активного частотно-независимого сопротивления на конце линии передачи определяется величиной этого сопротивления относительно волнового сопротивления.
Время, когда проявляется действие неоднородностей, определяется временем задержки сигнала в линиях передачи, расположенных до неоднородности и не зависит от величины их волновых сопротивлений:
В качестве примера определим параметры кольцевой корректирующей цепи по известным искажениям ПХ корректируемой системы. Пусть максимальные значения отклонений этой характеристики от l(t) составляют: , а длительность по уровню 0,1 от их максимальных значений не превышает 2tф. Пусть также t1 = tф = 50 пс, t2 — 105 пс, t3 = 500 пс, t4 = 605 пс, а линия имеет волновое сопротивление р — 50 Ом и выполнена из диэлектрика с относительной диэлектрической проницаемостью = 9.
Расстояния от входа линии до места включения неоднородностей определим из формулы , где с — скорость света в свободном пространстве. Из этой формулы находим: l1 = 0,25 см, l2 = 0,502 см, l3 = 2,025 см, l4= 2,5 см. Как видим, получены вполне приемлемые расстояния реализации кольцевой цепи в микроминиатюрном исполнении. Из формул, приведенных в таблице 1 определяем значения емкостей и индуктивностей: C1 = 0,2 пФ, С2 = 0,18 пФ, L1 = 0,3 нГн, L2 = 0,4 нГн. При р = 50 Ом ее сопротивление Z0 = 50 Ом.
Отметим, что при затянутых начальных участках фронта ПХ, во избежание ошибок в определении места включения неоднородностей в линию передачи, начало отсчета времени следует определять как точку пересечения касательной к фронту при с осью абсцисс.
5.4 Определение времени задержки через преобразование Гильберта
При анализе отраженных сигналов в пикосекундном диапазоне, благодаря высокой разрешающей способности, становится возможным определение внутренней структуры объектов или взаимного расположения отдельных частей объекта. Для этого необходимо определять соответственные времена задержки отраженных сигналов. При прохождении сигнала через объект и многократных отражениях сигнала форма отраженного сигнала значительно отличается от зондирующего сигнала. Возникает проблема в определении точек, между которыми необходимо производить отсчеты времени задержки.
Как следует из предыдущего материала, изменение времени задержки, приводящее к изменению фазовых свойств объекта, влияет на частотные характеристики объекта. Это означает, что характеристики объекта будут либо неоднозначными, при учете неминимально-фазовых свойств, либо искаженными, если их не учитывать.
Предлагается следующий алгоритм определения задержки [3]. Исследуемую характеристику можно изобразить в виде каскадного соединения двух частей. Первая часть описывается минимально-фазовым коэффициентом передачи , вторая часть — неминимально-фазовым коэффициентом передачи , рисунок 33.
Рисунок 33. Каскадное соединение минимально-фазового и
неминимально-фазового звеньев.
Модуль и аргумент первой передаточной функции, также, как и спектр минимально-фазовой части отраженного сигнала связаны преобразованием Гильберта:
Эта часть передаточной функции ответственна за искажения спектральных составляющих. В этой части передаточной функции появление выходного сигнала начинается в момент подачи входного сигнала, то есть задержка отсутствует.
Неминимально-фазовая часть представляет собой характеристику фазового корректора с передаточной функцией . Так как модуль коэффициента передачи этой функции равен единице, то его импульсная характеристика содержит , с соответствующим групповым временем задержки. Время задержки определяется по первому экстремуму ненеминимально-фазовой передаточной функции.
Алгоритм определения времени задержки следующий:
1. По отраженному сигналу через преобразование Фурье определить его спектр ;
2. Определить модуль спектра ;
3. Определить фазовую характеристику минимально-фазовой части через преобразование Гильберта
4. Найти спектр минимально-фазовой части ПФ
5. Найти спектр неминимально-фазовой части ПФ
6. Через обратное преобразование Фурье определить импульсную функцию
7. Определить задержку сигнала по первому экстремуму импульсной функции
Интуитивно было очевидно, что время задержки необходимо определять по первому отклику.
Рекомендуемые страницы:
Читайте также:
Пусть отрезок произвольной регулярной линии (рис. 3.1) включен между генератором и оконечным устройством, которое в дальнейшем будем называть нагрузкой. Предположим, что линия работает в одноволновом режиме, и по ней может распространяться волна основного типа, электрическое поле которой описывается векторной функцией  . Поскольку в конце линии в месте подключения нагрузки появляются новые границы раздела сред, то по сравнению с бесконечной линией в рассматриваемом случае изменяются краевые условия для векторов электромагнитного поля. В результате этого на конце линии возникает новая, соответствующая изменившимся краевым условиям структура поля. Поскольку в регулярной линии в общем случае может существовать бесконечное число типов волн, отличающихся друг от друга структурой полей, то образовавшееся после подключения нагрузки поле должно быть суперпозицией этих волн. Однако, если линия работает в одноволновом режиме, амплитуды векторов поля всех типов волн, кроме основного, экспоненциально убывают влинии по мере удаления от нагрузки. Поэтому, если плоскость T1 (рис. 3.1,а), перпендикулярная оси Z, расположена на таком расстоянии от нагрузки, при котором в этой плоскости можно пренебречь амплитудами векторов поля всех высших типов волн, то во всех точках линии, находящихся левее плоскости T1, кроме падающей будет распространяться лишь отраженная волна основного типа, электрическое поле которой описывается функцией
. Поскольку в конце линии в месте подключения нагрузки появляются новые границы раздела сред, то по сравнению с бесконечной линией в рассматриваемом случае изменяются краевые условия для векторов электромагнитного поля. В результате этого на конце линии возникает новая, соответствующая изменившимся краевым условиям структура поля. Поскольку в регулярной линии в общем случае может существовать бесконечное число типов волн, отличающихся друг от друга структурой полей, то образовавшееся после подключения нагрузки поле должно быть суперпозицией этих волн. Однако, если линия работает в одноволновом режиме, амплитуды векторов поля всех типов волн, кроме основного, экспоненциально убывают влинии по мере удаления от нагрузки. Поэтому, если плоскость T1 (рис. 3.1,а), перпендикулярная оси Z, расположена на таком расстоянии от нагрузки, при котором в этой плоскости можно пренебречь амплитудами векторов поля всех высших типов волн, то во всех точках линии, находящихся левее плоскости T1, кроме падающей будет распространяться лишь отраженная волна основного типа, электрическое поле которой описывается функцией  .
.

Рис. 3.1. а) Отрезок произвольной регулярной линии, включенный между генератором и нагрузкой; б) эквивалентная схема
Если в месте подключения нагрузки образуется такая структура поля, при которой в ее составе отсутствует волна основного типа, то отраженная волна в линии не появится. При этом, если отсутствуют потери в линии, вся переносимая падающей волной энергия поглощается в нагрузке, что следует из закона сохранения энергии. В этом случае говорят, что линия идеально согласована с нагрузкой или что линия работает в режиме бегущей волны.Аналогичные процессы происходят и в месте подключения генератора к линии.
Рассмотрим еще один случай, часто встречающийся при анализе цепей СВЧ. Пусть в регулярной линии передачи расположена какая-либо неоднородность (рис. 3.2,а), например, в прямоугольный волновод помещен некоторый объект, электродинамические параметры которого отличаются от параметров среды, заполняющей волновод (металлическая перегородка или штырь, диэлектрический цилиндр и др.). К этому же случаю можно отнести и соединение (стык) двух линий передачи с разной формой или разными размерами поперечного сечения. Во всех случаях в месте расположения неоднородности изменяется структура поля по сравнению с полем в регулярной линии. Вблизи неоднородности поле имеет сложную структуру, обусловленную суперпозицией волн, которые могут существовать в данной линии. Если линия работает в одноволновом режиме, то располагая перпендикулярно оси Z плоскости Ти Т1, на таком расстоянии от неоднородности, при котором в этих плоскостях можно пренебречь амплитудами векторов поля всех высших типов волн можно утверждать, что во всех точках линии, находящихся левее плоскости Т, появится (в общем случае) отраженная волна основного типа, напряженность электрического поля которой  , а во всех точках линии правее плоскости Т1появится прошедшая волна основного типа
, а во всех точках линии правее плоскости Т1появится прошедшая волна основного типа  . Поэтому обычно при рассмотрении процессов передачи энергии от генератора к нагрузке (рис.3.1, а) и исследовании влияния неоднородности на распространение энергии по линии (рис. 3.2,а) переходят к эквивалентной схеме (рис. 3.1,б и 3.2,б). При этом участки линии, где существуют лишь падающие и отраженные волны низшего типа, представляют эквивалентной линией. Участок линии, находящийся левее плоскости Т (рис. 3.1, а) с подключенным генератором и участок линии, находящийся правее плоскости Т1 с подключенной нагрузкой, представляют в виде эквивалентных двухполюсников (устройство с одним входом). Участок линии, содержащий неоднородность и находящийся между плоскостями Т и Т1 (рис. 3.2, а), представляют в виде эквивалентного четырехполюсника (устройства, имеющего вход и выход). Из теории линейных электрических цепей известно, что двухполюсники и четырехполюсники могут быть представлены в виде эквивалентных схем (схем замещения), состоящих из сосредоточенных элементов L, С, R. Например, на рис. 3.1,б двухполюсник, представляющий отрезок линии с подключенной нагрузкой, изображен в виде комплексного сопротивления ZH, а отрезок с подключенным генератором — в виде генератора напряжения с внутренним сопротивлением
. Поэтому обычно при рассмотрении процессов передачи энергии от генератора к нагрузке (рис.3.1, а) и исследовании влияния неоднородности на распространение энергии по линии (рис. 3.2,а) переходят к эквивалентной схеме (рис. 3.1,б и 3.2,б). При этом участки линии, где существуют лишь падающие и отраженные волны низшего типа, представляют эквивалентной линией. Участок линии, находящийся левее плоскости Т (рис. 3.1, а) с подключенным генератором и участок линии, находящийся правее плоскости Т1 с подключенной нагрузкой, представляют в виде эквивалентных двухполюсников (устройство с одним входом). Участок линии, содержащий неоднородность и находящийся между плоскостями Т и Т1 (рис. 3.2, а), представляют в виде эквивалентного четырехполюсника (устройства, имеющего вход и выход). Из теории линейных электрических цепей известно, что двухполюсники и четырехполюсники могут быть представлены в виде эквивалентных схем (схем замещения), состоящих из сосредоточенных элементов L, С, R. Например, на рис. 3.1,б двухполюсник, представляющий отрезок линии с подключенной нагрузкой, изображен в виде комплексного сопротивления ZH, а отрезок с подключенным генератором — в виде генератора напряжения с внутренним сопротивлением  .
.

Рис. 3.2. а) Неоднородность в регулярной линии передачи б) эквивалентная схема
Отметим, что поскольку амплитуда и фаза векторов электромагнитного поля как отраженной волны, так и прошедшей, зависят от конструкции неоднородности в линии или конструкции оконечного устройства, то параметры эквивалентных схем или элементы матриц, описывающих двухполюсники или четырехполюсники, могут быть определены либо с помощью решения соответствующей электродинамической задачи, либо с помощью эксперимента.
Рассмотрим передачу энергии от генератора к нагрузке по линии (рис. 3.1, а). На рис. 3.1,б показана эквивалентная схема для этого случая. Пусть отрезок эквивалентной линии без потерь  длиной l, имеющий волновое сопротивление ZB, возбуждается генератором напряжения с внутренним сопротивлением ZГ =ZB. К концу отрезка подключена нагрузка ZH. Генератор создает падающую волну, описываемую функциями
длиной l, имеющий волновое сопротивление ZB, возбуждается генератором напряжения с внутренним сопротивлением ZГ =ZB. К концу отрезка подключена нагрузка ZH. Генератор создает падающую волну, описываемую функциями  и
и  . Комплексную амплитуду напряжения падающей волны можно записать в виде:
. Комплексную амплитуду напряжения падающей волны можно записать в виде:
 (3.6)
(3.6)
где  и
и  — модуль и начальная фаза функции
— модуль и начальная фаза функции  в начале координат (при z = 0). Начало оси Z совпадает с плоскостью Т1, а ее положительное направление указано на рис. 3.1. В общем случае подключение к линии произвольной нагрузки вызывает появление в линии отраженной волны, описываемой функциями
в начале координат (при z = 0). Начало оси Z совпадает с плоскостью Т1, а ее положительное направление указано на рис. 3.1. В общем случае подключение к линии произвольной нагрузки вызывает появление в линии отраженной волны, описываемой функциями  и
и  . Комплексную амплитуду напряжения отраженной волны можно записать в виде:
. Комплексную амплитуду напряжения отраженной волны можно записать в виде:
 (3.7)
(3.7)
где  и
и  — модуль и начальная фаза функции
— модуль и начальная фаза функции  при z = 0. Отношение комплексной амплитуды напряжения отраженной волны к комплексной амплитуде напряжения падающей волны в произвольном поперечном сечении линии передачи называют коэффициентом отражения по напряжению в указанном сечении:
при z = 0. Отношение комплексной амплитуды напряжения отраженной волны к комплексной амплитуде напряжения падающей волны в произвольном поперечном сечении линии передачи называют коэффициентом отражения по напряжению в указанном сечении:
 , (3.8)
, (3.8)
где  — коэффициент отражения по напряжению в месте подключения нагрузки
— коэффициент отражения по напряжению в месте подключения нагрузки  ;
;  , а
, а  .
.
Полное напряжение  и полный ток
и полный ток  ,возникающей в произвольном поперечном сечении линии, являются суммой напряжений и токов падающей и отраженной волн соответственно в этом сечении:
,возникающей в произвольном поперечном сечении линии, являются суммой напряжений и токов падающей и отраженной волн соответственно в этом сечении:
 , (3.9)
, (3.9)
 , (3.10)
, (3.10)
где использованы соотношения 
 .
.
Средняя за период мощность, проходящая через произвольное поперечное сечение линии, вычисляется по формуле:
 (3.11)
(3.11)

Из формулы (3.9), учитывая формулу (3.8), определим модуль полного напряжения в произвольном сечении линии:
 (3.12)
(3.12)

Рис. 3.3. Зависимость отношения полного напряжения к комплексной амплитуде напряжения падающей волны от координаты z
На рис. 3.3 показана зависимость величины  от координаты z, вычисленная по (3.12). Как видно, отраженная волна суммируется с падаю-щей, что приводит к образованию повторяющихся минимумов и максимумов. При этом минимумы, равные 1-Г0, наблюдаются в сечениях линий, имеющих координату
от координаты z, вычисленная по (3.12). Как видно, отраженная волна суммируется с падаю-щей, что приводит к образованию повторяющихся минимумов и максимумов. При этом минимумы, равные 1-Г0, наблюдаются в сечениях линий, имеющих координату  , а максимумы, равные 1+Г0 — в сечениях с координатой
, а максимумы, равные 1+Г0 — в сечениях с координатой  , где п=2,3. Расстояние между ближайшими максимумами (или минимумами) всегда одно и то же и равно половине длины волны, соответствующей распространяющемуся типу волны в линии. В инженерной практике режим работы линии обычно характеризуют коэффициентом бегущей волны (КБВ):
, где п=2,3. Расстояние между ближайшими максимумами (или минимумами) всегда одно и то же и равно половине длины волны, соответствующей распространяющемуся типу волны в линии. В инженерной практике режим работы линии обычно характеризуют коэффициентом бегущей волны (КБВ):
 (3.13)
(3.13)
где  и
и  — минимальное и максимальное значения модуля полного напряжения.
— минимальное и максимальное значения модуля полного напряжения.
Часто вместо КБВ используют обратную величину, называемую коэффициентом стоячей волны КСВ=1/КБВ. В линии, идеально согласованной с нагрузкой, имеется только падающая волна (отраженная волна отсутствует) Г0=0; КБВ=КСВ=1. Такой режим работы линии называют режимом бегущей волны.Приполном отражении падающей волны от нагрузки, когда U0 отр=U0 пад, Г0=1, КБВ = 0, КСВ = ∞. Такой режим называют режимом стоячей волны.
Следует отметить, что изображенная на рис. 3.3 зависимость получена в пренебрежении тепловыми потерями в линии. В этом случае – как модуль коэффициента отражения  , так и величины КСВ и КБВ не изменяются вдоль линии. При учете тепловых потерь в линии
, так и величины КСВ и КБВ не изменяются вдоль линии. При учете тепловых потерь в линии  в формулах (3.6)-(3.11) следует заменить β на
в формулах (3.6)-(3.11) следует заменить β на  , где
, где  — коэффициент распространения рассматриваемой волны в линии. При этом амплитуды напряжений, соответствующих падающей и отраженной волнам, экспоненциально убывают вдоль направления распространения волны в линии. Коэффициент отражения (3.8) вычисляется по формуле:
— коэффициент распространения рассматриваемой волны в линии. При этом амплитуды напряжений, соответствующих падающей и отраженной волнам, экспоненциально убывают вдоль направления распространения волны в линии. Коэффициент отражения (3.8) вычисляется по формуле:
 (3.14)
(3.14)
Поскольку в данном случае  , то в (3.12) следует заменить
, то в (3.12) следует заменить  на
на  и β на β1. Распределение модуля полного напряжения вдоль линии с учетом тепловых потерь построено на рис. 3.4 (пунктирная линия).
и β на β1. Распределение модуля полного напряжения вдоль линии с учетом тепловых потерь построено на рис. 3.4 (пунктирная линия).

Рис. 3.4. Распределение модуля полного напряжения вдоль линии с учетом тепловых потерь
В линии с тепловыми потерями КБВ следует определять как ношение обязательно соседних минимального и максимального значений модуля полного напряжения. При удалении от нагрузки величина максимумов уменьшается, а минимумов возрастает, т.е. КБВ возрастает.
Режим работы такой линии можно характеризовать двумя значениями КБВ: у нагрузки (КБВН) и у генератора (КБВг), которые связаны формулой:
 (3.15)
(3.15)
Из (3.13) следует связь между Г0 и КБВН:
 (3.16)
(3.16)
Еще одной важной характеристикой процесса передачи энергии от генератора в нагрузку с помощью линии является коэффициент полезного действия(КПД), равный отношению средней мощности  , поступающей в нагрузку, к средней мощности
, поступающей в нагрузку, к средней мощности  , переносимой падающей волной, в начале линии (при z=l). Если в линии отсутствует отраженная волна, то вся мощность, переносимая падающей волной в точках подключения нагрузки, поступает в нагрузку, т.е.:
, переносимой падающей волной, в начале линии (при z=l). Если в линии отсутствует отраженная волна, то вся мощность, переносимая падающей волной в точках подключения нагрузки, поступает в нагрузку, т.е.:
 (3.17)
(3.17)
Согласно (3.11), появление отраженной от нагрузки волны приводит к дополнительному уменьшению средней мощности, поступающей внагрузку, в  раз. Используя (3.17), запишем формулу для КПД:
раз. Используя (3.17), запишем формулу для КПД:
 . (3.18)
. (3.18)
Определим среднюю мощность тепловых потерь в линии (рис.3.1,а):
 (3.19)
(3.19)
где  — средняя мощность, поступающая от генератора на вход линии; она равна средней мощности, отдаваемой генератором падающей волне
— средняя мощность, поступающая от генератора на вход линии; она равна средней мощности, отдаваемой генератором падающей волне  минус средняя мощность
минус средняя мощность  , переносимая отраженной волной при
, переносимая отраженной волной при  (предполагается, что генератор идеально согласован с линией). Поэтому:
(предполагается, что генератор идеально согласован с линией). Поэтому:
 (3.20)
(3.20)
Подставляя (3.20) и (3.17) в (3.19), получаем:
 (3.21)
(3.21)
На рис. 3.5 показаны рассчитанные по (3.18) и (3.21) графики зависимости КПД и отношения  от КБВН при разных значениях полного затухания линии
от КБВН при разных значениях полного затухания линии  [дБ]. Как видно, полная передача энергии от генератора нагрузки (КПД=1) будет при идеальном согласовании нагрузки с линией (Г0=0 и КБВН=1) и отсутствии потерь в линии αl=0). Отметим, что даже при отсутствии потерь в линии при КБВН<1 КПД<1 из-за отражения части мощности от нагрузки.
[дБ]. Как видно, полная передача энергии от генератора нагрузки (КПД=1) будет при идеальном согласовании нагрузки с линией (Г0=0 и КБВН=1) и отсутствии потерь в линии αl=0). Отметим, что даже при отсутствии потерь в линии при КБВН<1 КПД<1 из-за отражения части мощности от нагрузки.

Рис. 3.5. Графики зависимости КПД и отношения Рсрпот/ Рсрпад от КБВН
Как уже отмечалось, максимальная величина мощности, которую может переносить падающая волна, ограничена тем значением, при котором в линии происходит электрический пробой или разрушение диэлектрического заполнения (тепловой пробой). При возникновении пробоя передача энергии по линии прекращается. Наличие отраженной волны в линии приводит к появлению в ней областей с повышенным значением напряжения (рис.3.3) по отношению к напряжению падающей волны, что приводит к уменьшению электрической прочности линии. Например, при полном отражении от нагрузки (Г0 = 1) пробой в линии наступает при мощности падающей волны, составляющей 0,25 мощности падающей волны, приводящей к пробою всогласованной линии, когда Г0 = 0. Нередко волна, отраженная от нагрузки, оказывается причиной затягивания частоты генератора, питающего линию, при этом генератор начинает работать на частоте, несколько отличающейся от требуемой. Таким образом, при передаче энергии от генератора к нагрузке с помощью линии наиболее выгоден режим бегущей волны в линии, когда Г0 = 0 и КБВН = 1. В этом случае отсут?
