Какими свойствами обладают логарифмы
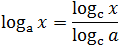
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Зачем в жизни нужны логарифмы?
Я уже говорил, что математики СУПЕРленивые люди? Это правда.
Вот представь себе, им лень умножать и они придумали логарифмы, которые позволяют заменить умножение сложением!
Им еще больше лень возводить в степень и они используют логарифмы, чтобы заменить возведение в степень умножением или делением!
То есть они используют логарифмы, чтобы быстро проделывать громоздкие вычисления.
Круто, да?
Как научиться решать логарифмы?
Логарифмы – ОЧЕНЬ ПРОСТАЯ ТЕМА!
Чтобы понять как их решать – нужно: разобраться со свойствами логарифма и понимать что как называется,понимать разницу между видами логарифмов (десятичными и натуральными).
Ну и уметь возводить число в степень, знать таблицу умножения (а это ты точно умеешь).
Все. Больше ничего не нужно.
Прочитай эту статью, обязательно реши примеры и решение логарифмов навсегда станет для тебя задачкой easy-peasy lemon squeezy — очень легкой 🙂
СОДЕРЖАНИЕ СТАТЬИ
Что такое логарифм?
Для начинающих объясним все человеческим языком. Логарифмы – очень простая тема. Чтобы понять как их решать – нужно всего лишь разобраться что как называется, знать таблицу умножения и уметь возводить в число в степень. Все. Больше ничего не нужно.
Начнем с простого. Как решить уравнение ?
Очень легко – просто ответь на вопрос в какую степень нужно возвести число чтобы получить ? Решаем методом подбора: два в первой степени – нет, два во второй степени – нет, два в третей степени – ДА! Двойку нужно возвести в ТРЕТЬЮ степень, чтобы получить восемь ( ) и значит решением уравнения будет число три ( ).
Следующий вопрос. Как решить уравнение ?
Опять просто ответь на вопрос в какую степень нужно возвести число , чтобы получить число ? Попытаемся подобрать: два во второй степени равно четыре – мало, два в третьей степени равно восемь – много. Метод подбора сразу ответ не дает… Да и вообще, в этом случае подобрать решение не получится – ведь это не только нецелое число, это число даже не рациональное. Для нахождения таких решений было придумано понятие логарифм: . В общем виде он записывается так:

То есть логарифм – это степень, в которую нужно возвести основание , чтобы получить аргумент .
Вернёмся к . Если ты посчитаешь на калькуляторе, то получишь и т.д. Это число иррациональное. Оно мало того, что не подбирается, оно еще и не кончается…
Ну и как с такими числами работать? Как их запоминать? Как их записывать?
В нашем случае решение уравнения можно записать как или как .
Согласись второе выражение гораздо удобнее, чем первое. И оно, кстати, абсолютно точное.
Словами это произносится как: «Решением уравнения два в степени икс равно пяти является логарифм пяти по основанию два, или логарифм по основанию два от пяти».
Кстати, а ты заметил что и у степени числа и у логарифма основание всегда находится «ВНИЗУ». Легко запомнить правда? А вот «вверху», у степени находится ее показатель, а у логарифма – аргумент.
Выражение можно также записать в виде . Читается так: «Логарифм восьми по основанию два равен трем» или «Логарифм по основанию два от восьми равен трем».
Теперь более общая запись:

Читается так: «Логарифм по основанию от равен », и означает: «Чтобы получить число , нужно число возвести в степень »:

Иными словами, – это степень, в которую нужно возвести , чтобы получить .
Примеры вычисления логарифмов
- , так как число нужно возвести во вторую степень, чтобы получить .
- Чему равен ? Заметим, что , тогда , то есть нужно возвести в степень , чтобы получить .
- А чему равен ? Обращать внимание нужно, в первую очередь, на основание. Возможно ли представить как в какой-то степени? Да, возможно: запишем это число в виде обычной дроби: . Значит, .
- Еще пример. Чему равен ? В какую степень надо возвести , чтобы получить ? Вспоминаем, что любое число в нулевой степени равно (подробнее читай в разделе «Степень и ее свойства»). Значит, . Более того, логарифм с любым основанием от единицы равен .
- . В этом случае аргумент равен корню основания: . Но мы помним, что корень тоже можно представить в виде степени (с дробным показателем): .
Попробуй найти следующие логарифмы самостоятельно:
Ответы:
Десятичные логарифмы
Логарифм по основанию называется десятичным логарифмом и записывается упрощенно: вместо , например:
- ;
- ;
- ;
- ;
- .
Когда нужная степень не подбирается
Как я уже говорил, далеко не всегда удается подобрать такую степень. Но это не значит, что такого числа не существует, просто его можно вычислить только на калькуляторе.
Например, . Видим, что это число расположено между и , и это понятно: ведь это значит, чтобы получить , нужно возводить в степень больше , но меньше .
На ЕГЭ пользоваться калькулятором нельзя, но даже если бы было можно, нельзя записывать приближенные вычисления. Поэтому, если перед нами задача первой части, ответ обязательно должен получиться «хороший», и его можно посчитать в уме. В письменной части могут попасться и «плохие» числа; в этом случае пугаться не нужно, в ответе можно просто написать логарифм. Например, ответ вполне может выглядеть так: , или даже так: .
Получается, что теперь мы можем мнгновенно записать решение любого элементарного показательного уравнения:
? Легко: .
?
? . И так далее.
Но увлекаться и халтурить тоже не стоит – если в ответе оставить , высший балл за задачу не поставят. То есть, если ответ возможно упростить и представить в виде рационального числа, это обязательно нужно будет сделать. Потренируйся на следующих простых примерах:
Примеры для самостоятельной работы
Ответы на примеры для самостоятельной работы:
- ;
- , но никак не представить в виде степени четверки. Поэтому все просто: ;
- ;
- . Как и в примере 2, здесь придумать степень не получится, поэтому ;
- ;
- . Очевидно, и здесь степень придумать не удастся: .
Кстати, ответы типа или можно упростить – сделать числа поменьше. Как это сделать, и зачем – об этом чуть позже, в разделе «Свойства логарифмов».
Область допустимых значений (ОДЗ) логарифма
Теперь поговорим об ограничениях (ОДЗ – область допустимых значений переменных).
Мы помним, что, например, квадратный корень нельзя извлекать из отрицательных чисел; или если у нас дробь, то знаменатель не может быть равен нулю. Подобные ограничения есть и у логарифмов:

То есть и аргумент, и основание должны быть больше нуля, а основание еще и не может равняться .
Почему так?
Начнем с простого: допустим, что . Тогда, например, число не существует, так как в какую бы степень мы не возводили , всегда получается . Более того, не существует ни для какого . Но при этом может равняться чему угодно (по той же причине – в любой степени равно ). Поэтому объект не представляет никакого интереса, и его просто выбросили из математики.
Похожая проблема у нас и в случае : в любой положительной степени – это , а в отрицательную его вообще нельзя возводить, так как получится деление на ноль (напомню, что ).
При мы столкнемся с проблемой возведения в дробную степень (которая представляется в виде корня: . Например, (то есть ), а вот не существует.
Поэтому и отрицательные основания проще выбросить, чем возиться с ними.
Ну а поскольку основание a у нас бывает только положительное, то в какую бы степень мы его ни возводили, всегда получим число строго положительное. Значит, аргумент должен быть положительным. Например, не существует, так как ни в какой степени не будет отрицательным числом (и даже нулем, поэтому тоже не существует).
В задачах с логарифмами первым делом нужно записать ОДЗ. Приведу пример:
Решим уравнение .
Вспомним определение: логарифм – это степень, в которую надо возвести основание , чтобы получить аргумент . И по условию, эта степень равна : .
Получаем обычное квадратное уравнение: . Решим его с помощью теоремы Виета: сумма корней равна , а произведение . Легко подобрать, это числа и .
Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу. Почему? Давайте подумаем, что будет, если подставить эти корни в начальное уравнение?
— верно.
– это явно неверно, так как основание не может быть отрицательным, то есть корень – «сторонний».
Чтобы избежать таких неприятных подвохов, нужно записать ОДЗ еще до начала решения уравнения:
Тогда, получив корни и , сразу отбросим корень , и напишем правильный ответ.
Пример 1 (попробуй решить самостоятельно):
Найдите корень уравнения . Если корней несколько, в ответе укажите меньший из них.
Решение:
.
В первую очередь напишем ОДЗ:
Теперь вспоминаем, что такое логарифм: в какую степень нужно возвести основание , чтобы получить аргумент ? Во вторую. То есть:
Казалось бы, меньший корень равен . Но это не так: согласно ОДЗ корень – сторонний, то есть это вообще не корень данного уравнения. Таким образом, уравнение имеет только один корень: .
Ответ: .
Основное логарифмическое тождество
Вспомним определение логарифма в общем виде:
Подставим во второе равенство вместо логарифм:
Это равенство называется основным логарифмическим тождеством. Хотя по сути это равенство – просто по-другому записанное определение логарифма:
– это степень, в которую нужно возвести , чтобы получить .
Например:
Реши еще следующие примеры:
Пример 2.
Найдите значение выражения .
Решение:
Вспомним правило из раздела «Степень и ее свойства»: , то есть, при возведении степени в степень показатели перемножаются. Применим его:
.
Пример 3.
Докажите, что .
Решение:
, ч.т.д.
Свойства логарифмов
К сожалению, задачи не всегда такие простые – зачастую сперва нужно упростить выражение, привести его к привычному виду, и только потом будет возможно посчитать значение. Это проще всего сделать, зная свойства логарифмов. Так что давай выучим основные свойства логарифмов. Каждое из них я буду доказывать, ведь любое правило проще запомнить, если знать, откуда оно берется.
Все эти свойства нужно обязательно запомнить, без них большинство задач с логарифмами решить не получится.
А теперь обо всех свойствах логарифмов подробнее.
Свойство 1:
Доказательство:
Пусть , тогда .
Имеем: , ч.т.д.
Свойство 2: Сумма логарифмов
Сумма логарифмов с одинаковыми основаниями равна логарифму произведения: .
Доказательство:
Пусть , тогда . Пусть , тогда .
Имеем:
, ч.т.д.
Пример: Найдите значение выражения: .
Решение: .
Только что выученная формула помогает упростить сумму логарифмов, а не разность, так что сразу эти логарифмы не объединить. Но можно сделать наоборот – «разбить» первый логарифм на два:А вот обещанное упрощение:
.
Зачем это нужно? Ну например: чему равно ?
.
Теперь очевидно, что .
Теперь упрости сам:
Задачи:
- .
- .
- .
- .
Ответы:
1.
2.
3.
4.
Свойство 3: Разность логарифмов:
Доказательство:
Все точно так же, как и в пункте 2:
Пусть , тогда .
Пусть , тогда . Имеем:
, ч.т.д.
, ч.т.д.
Пример из прошлого пункта теперь становится еще проще:
Пример посложнее: . Догадаешься сам, как решить?
Здесь нужно заметить, что у нас нету ни одной формулы про логарифмы в квадрате. Это что-то сродни выражению – такое сразу не упростить.
Поэтому отвлечемся от формул про логарифмы, и подумаем, какие вообще формулы мы используем в математике чаще всего? Еще начиная с 7 класса!
Это – формулы сокращенного умножения. Нужно привыкнуть к тому, что они везде! И в показательных, и в тригонометрических, и в иррациональных задачах они встречаются. Поэтому их нужно обязательно помнить.
Нажми на ссылку «Формулы сокращенного умножения», и внимательно на них посмотри. Какую из них можно применить здесь?
Если присмотреться к первым двум слагаемым, становится ясно, что это разность квадратов:
.
Дальше все просто – применяем только что выученные правила 2 и 3. Что получилось?
Ответ для проверки:
Упрости сам.
Примеры
Ответы.
1.
2.
3.
4.
5.
Свойство 4: Вынесение показателя степени из аргумента логарифма:
Доказательство: И здесь тоже используем определение логарифма:пусть , тогда . Имеем: , ч.т.д.
Можно понять это правило так:
То есть степень аргумента выносится вперед логарифма, как коэффициент.
Пример: Найдите значение выражения .
Решение: .
Реши сам:
Примеры:
Ответы:
1. .
2. .
3.
Свойство 5: Вынесение показателя степени из основания логарифма:
Доказательство: Пусть , тогда .
Имеем: , ч.т.д.
Запоминаем: из основания степень выносится как обратное число, в отличии от предыдущего случая!
Свойство 6: Вынесение показателя степени из основания и аргумента логарифма:
Или если степени одинаковые: .
Свойство 7: Переход к новому основанию:
Доказательство: Пусть , тогда .
Имеем: , ч.т.д.
Свойство 8: Замена местами основания и аргумента логарифма:
Доказательство: Это частный случай формулы 7: если подставить , получим: , ч.т.д.
Рассмотрим еще несколько примеров.
Пример 4.
Найдите значение выражения .
Решение:
Используем свойство логарифмов № 2 – сумма логарифмов с одинаковым основанием равна логарифму произведения:
.
Пример 5.
Найдите значение выражения .
Решение:
Используем свойство логарифмов № 3 и № 4:
.
Пример 6.
Найдите значение выражения .
Решение:
Используем свойство № 7 – перейдем к основанию 2:
Пример 7.
Найдите значение выражения .
Решение:
Как тебе статья?
Если ты читаешь эти строки, значит ты прочитал всю статью.
И это круто!
А теперь расскажи нам как тебе статья?
Научился ты решать логарифмы? Если нет, то в чем проблема?
Пиши нам в комментах ниже.
Мы будем рады прочитать.
И, да, удачи на экзаменах.
На ЕГЭ и ОГЭ и вообще в жизни
ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!
Стать учеником YouClever,
Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц»,
А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.
можно кликнув по этой ссылке.
2 февраля 2017
- Материалы к уроку
-
![[Скачать все формулы] Скачать: [Скачать все формулы]](https://www.berdov.com/img/file.png)
Скачать все формулы
Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать. Но поскольку логарифмы — это не совсем обычные числа, здесь есть свои правила, которые называются основными свойствами.
Эти правила обязательно надо знать — без них не решается ни одна серьезная логарифмическая задача. К тому же, их совсем немного — все можно выучить за один день. Итак, приступим.
Сложение и вычитание логарифмов
Рассмотрим два логарифма с одинаковыми основаниями: logax и logay. Тогда их можно складывать и вычитать, причем:
- logax + logay = loga (x · y);
- logax − logay = loga (x : y).
Итак, сумма логарифмов равна логарифму произведения, а разность — логарифму частного. Обратите внимание: ключевой момент здесь — одинаковые основания. Если основания разные, эти правила не работают!
Эти формулы помогут вычислить логарифмическое выражение даже тогда, когда отдельные его части не считаются (см. урок «Что такое логарифм»). Взгляните на примеры — и убедитесь:
Задача. Найдите значение выражения: log6 4 + log6 9.
Поскольку основания у логарифмов одинаковые, используем формулу суммы:
log6 4 + log6 9 = log6 (4 · 9) = log6 36 = 2.
Задача. Найдите значение выражения: log2 48 − log2 3.
Основания одинаковые, используем формулу разности:
log2 48 − log2 3 = log2 (48 : 3) = log2 16 = 4.
Задача. Найдите значение выражения: log3 135 − log3 5.
Снова основания одинаковые, поэтому имеем:
log3 135 − log3 5 = log3 (135 : 5) = log3 27 = 3.
Как видите, исходные выражения составлены из «плохих» логарифмов, которые отдельно не считаются. Но после преобразований получаются вполне нормальные числа. На этом факте построены многие контрольные работы. Да что контрольные — подобные выражения на полном серьезе (иногда — практически без изменений) предлагаются на ЕГЭ.
Вынесение показателя степени из логарифма
Теперь немного усложним задачу. Что, если в основании или аргументе логарифма стоит степень? Тогда показатель этой степени можно вынести за знак логарифма по следующим правилам:
- logaxn = n · logax;
-
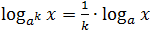
-
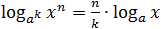
Несложно заметить, что последнее правило следует их первых двух. Но лучше его все-таки помнить — в некоторых случаях это значительно сократит объем вычислений.
Разумеется, все эти правила имеют смысл при соблюдении ОДЗ логарифма: a > 0, a ≠ 1, x > 0. И еще: учитесь применять все формулы не только слева направо, но и наоборот, т.е. можно вносить числа, стоящие перед знаком логарифма, в сам логарифм. Именно это чаще всего и требуется.
Задача. Найдите значение выражения: log7 496.
Избавимся от степени в аргументе по первой формуле:
log7 496 = 6 · log7 49 = 6 · 2 = 12
Задача. Найдите значение выражения:
[Подпись к рисунку]
Заметим, что в знаменателе стоит логарифм, основание и аргумент которого являются точными степенями: 16 = 24; 49 = 72. Имеем:
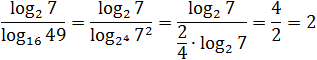 [Подпись к рисунку]
[Подпись к рисунку]
Думаю, к последнему примеру требуются пояснения. Куда исчезли логарифмы? До самого последнего момента мы работаем только со знаменателем. Представили основание и аргумент стоящего там логарифма в виде степеней и вынесли показатели — получили «трехэтажную» дробь.
Теперь посмотрим на основную дробь. В числителе и знаменателе стоит одно и то же число: log2 7. Поскольку log2 7 ≠ 0, можем сократить дробь — в знаменателе останется 2/4. По правилам арифметики, четверку можно перенести в числитель, что и было сделано. В результате получился ответ: 2.
Переход к новому основанию
Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. А что, если основания разные? Что, если они не являются точными степенями одного и того же числа?
На помощь приходят формулы перехода к новому основанию. Сформулируем их в виде теоремы:
Пусть дан логарифм logax. Тогда для любого числа c такого, что c > 0 и c ≠ 1, верно равенство:
[Подпись к рисунку]
В частности, если положить c = x, получим:
[Подпись к рисунку]
Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.
Эти формулы редко встречается в обычных числовых выражениях. Оценить, насколько они удобны, можно только при решении логарифмических уравнений и неравенств.
Впрочем, существуют задачи, которые вообще не решаются иначе как переходом к новому основанию. Рассмотрим парочку таких:
Задача. Найдите значение выражения: log5 16 · log2 25.
Заметим, что в аргументах обоих логарифмов стоят точные степени. Вынесем показатели: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;
А теперь «перевернем» второй логарифм:
![]() [Подпись к рисунку]
[Подпись к рисунку]
Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами.
Задача. Найдите значение выражения: log9 100 · lg 3.
Основание и аргумент первого логарифма — точные степени. Запишем это и избавимся от показателей:
![]() [Подпись к рисунку]
[Подпись к рисунку]
Теперь избавимся от десятичного логарифма, перейдя к новому основанию:
![]() [Подпись к рисунку]
[Подпись к рисунку]
Основное логарифмическое тождество
Часто в процессе решения требуется представить число как логарифм по заданному основанию. В этом случае нам помогут формулы:
- n = logaan
-
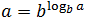
В первом случае число n становится показателем степени, стоящей в аргументе. Число n может быть абсолютно любым, ведь это просто значение логарифма.
Вторая формула — это фактически перефразированное определение. Она так и называется: основное логарифмическое тождество.
В самом деле, что будет, если число b возвести в такую степень, что число b в этой степени дает число a? Правильно: получится это самое число a. Внимательно прочитайте этот абзац еще раз — многие на нем «зависают».
Подобно формулам перехода к новому основанию, основное логарифмическое тождество иногда бывает единственно возможным решением.
Задача. Найдите значение выражения:
[Подпись к рисунку]
Заметим, что log25 64 = log5 8 — просто вынесли квадрат из основания и аргумента логарифма. Учитывая правила умножения степеней с одинаковым основанием, получаем:
![]() [Подпись к рисунку]
[Подпись к рисунку]
Если кто-то не в курсе, это была настоящая задача из ЕГЭ 🙂
Логарифмическая единица и логарифмический ноль
В заключение приведу два тождества, которые сложно назвать свойствами — скорее, это следствия из определения логарифма. Они постоянно встречаются в задачах и, что удивительно, создают проблемы даже для «продвинутых» учеников.
- logaa = 1 — это логарифмическая единица. Запомните раз и навсегда: логарифм по любому основанию a от самого этого основания равен единице.
- loga 1 = 0 — это логарифмический ноль. Основание a может быть каким угодно, но если в аргументе стоит единица — логарифм равен нулю! Потому что a0 = 1 — это прямое следствие из определения.
Вот и все свойства. Обязательно потренируйтесь применять их на практике! Скачайте шпаргалку в начале урока, распечатайте ее — и решайте задачи.
Смотрите также:
- Тест к уроку «Что такое логарифм» (тяжелый)

- Как решать простейшие логарифмические уравнения

- Пробный ЕГЭ 2012. Вариант 10 (без логарифмов)

- Пробный ЕГЭ-2011 по математике, вариант №6

- Показательные функции в задаче B15

- Процент: налоги и зарплата. Считаем с помощью коэффициентов

