Какими свойствами обладает выборочное среднее
Основной аналитической средней является средняя арифметическая или средняя выборочная.
Средняя выборочная – это одна из основных статистик распределения, которая характеризует среднее значение рассматриваемых выборочных данных.
Для нахождения средней выборочной существуют несколько формул, применение которых зависит от того, в каком виде представлены выборочные данные.
Если выборочные данные записаны в виде произвольной последовательности чисел: х1, х2, … , хn, то для нахождения средней выборочной используется обычная формула, называемая формулой простой средней
(5.1)
Если выборочные данные записаны в виде вариационного дискретного ряда распределения частот
| Варианты хi | x1 | x2 | … | xm |
| Частоты ni | n1 | n2 | … | nm |
то для нахождения средней выборочной используется формула, называемая формулой взвешенной средней
(5.2).
Очевидно, что если в вариационном ряде заданы не частоты, а частости, то формула (5.2) примет вид
(5.3).
Название формулы взвешенной средней связано с тем, что частоты niчасто называют весами, так как, по сути, они показывают какой вес имеет рассматриваемый вариант во всей совокупности, а сама операция умножения xini называется взвешиванием.
Для статистических данных, записанных в виде интервального ряда
| Интервалы | а1 – а2 | а2 – а3 | … | am − am+1 |
| Частоты интервалов | n1 | n2 | … | nm |
для вычисления средней арифметической используется формула, аналогичная формуле (5.2) с заменой варианты xiна zi – середину соответствующего интервала, именно
(5.4)
Необходимо отметить, что средняя выборочная обладает важной частной особенностью. Размерность средней выборочной совпадает с размерностью рассматриваемых выборочных данных.
Средняя выборочная является выборочным аналогом математического ожидания случайной величины, хотя эти характеристики имеют и принципиальные отличия. Если сравнить формулу для математического ожидания дискретной случайной величины и формулу (5.3), то внешняя схожесть этих формул очевидна. Однако в формуле для математического ожидания значения случайной величины умножаются на вероятности этих значений, а в формуле (5.3) значения вариант умножаются на относительные частоты этих вариант. В то же время следует отметить, что при определенных условиях, при неограниченном увеличении числа n средняя выборочная сходится по вероятности к математическому ожиданию (см. теорему Чебышева в параграфе 1). Поэтому при больших n среднюю выборочную считают приближенным значением математического ожидания или его оценкой.
Средняя выборочная обладает рядом свойств, аналогичных свойствам математического ожидания, а именно
1. Средняя выборочная постоянной равно самой этой постоянной.
2. Если все варианты умножить или разделить на одно и тоже число к, то будет выполнено равенство или более подробно , т.е. постоянную величину можно выносить за знак выборочной средней. Иначе говоря, если все варианты увеличить или уменьшить в одно и тоже число раз, то и средняя выборочная также увеличиться или уменьшится в это же число раз.
3. Если все варианты увеличить или уменьшить на одно и тоже число раз с, то и средняя выборочная увеличиться или уменьшится на это же число раз, т.е.
, так как .
4. Средняя выборочная алгебраической суммы двух (или нескольких) признаков равна алгебраической сумме средних выборочных этих признаков, т.е. .
5. Если выборочные данные разделены на некоторые группы, то общая средняя всех данных вычисляется по формуле
,
где r – число групп;
– средняя выборочная в j – ой группе (групповая средняя);
– сумма часто вариант, попавших в j – ую группу (объем группы).
6. Если все частоты вариантов умножить на одно и тоже число, то средняя выборочная не изменится.
7. Средняя выборочная отклонений вариантов от средней выборочной равна нулю, т.е. , так как
.
Пример 5.1. Найти среднюю арифметическую для
а) вариационного дискретного ряда
б) вариационного интервального ряда
| Интервалы | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 |
| Частоты интервалов |
Решение. а) Воспользуемся формулой (5.2), получим
.
б) Припишем к интервальному ряду строку с серединами интервалов и воспользуемся формулой (5.4), получим
| Интервалы | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 |
| Частоты интервалов | |||||
| zi |
и . ■
3.2. Порядковые средние.
Особое место в математической статистике занимают порядковыеили структурные средние, т.е. характеристики, зависящие от порядка следования вариант в вариационном ряде. Самыми известными из порядковых средних являются мода и медиана.
Выборочной модой (или просто модой) называется одна из основных статистик распределения, которая характеризует наиболее часто встречающееся значение признака.
Для дискретного ряда мода равна варианту с наибольшей частотой. Например, для дискретного вариационного ряда из примера 5.1 мода = 6, так как у этого варианта наибольшая частота.
Для нахождения моды в случае интервального ряда вначале находят модальный интервал[ap – ap+1], т.е. интервал с наибольшей частотой. Мода находится внутри модального интервала по формуле:
,(5.6)
где ap – левая граница модального интервала;
np – частота модального интервала;
np-1 – частота интервала, предшествующего модальному;
np+1 – частота интервала, последующего за модальным;
h – длина интервала.
В формуле (5.6) все частоты можно заменить на частости, соответствующие интервалов, от этого значение моды не измениться.
Мода может быть найдена графическим путем по гистограмме. Рассмотрим гистограмму распределения частот интервального ряда. Выделим на этой гистограмме прямоугольник с наибольшей высотой. Соединим прямыми линиями две вершины этого прямоугольника с вершинами соседних прямоугольников, как показано на следующем рисунке
Абсцисса точки пересечения построенных прямых равна моде рассматриваемого вариационного ряда. Формула (5.6) получена из данного графического представления. Если с помощью методов аналитической геометрии найти уравнения двух прямых, построенных по двум точкам, то точка их пересечения имеет первую координату, равную моде.
Иногда упрощают нахождение моды, предполагая, что она приближенно равна середине модального интервала.
Пример 5.2. Для интервального ряда из примера 10 аналитически и графически найти моду и сравнить ее с серединой модального интервала.
Решение.Для интервального ряда
| Интервалы | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 |
| Частоты интервалов |
модальным интервалом будет интервал [5 − 7], как интервал с наибольшей частотой.
Выпишем данные, необходимые для нахождения моды:
ap = 5; np = 7; np-1 = 6; np+1 = 3; h = 7 – 5 = 2.
Подставляем данные в формулу (5.6), получаем
.
Середина модального интервала равна z = 6, как видим, это достаточно грубое приближение для моды.
Можно построить гистограмму и найти моду графически.
Мода – это единственная из основных статистик, которая может иметь несколько значений для одного вариационного ряда. Если в вариационном ряде наибольшая частота будет соответствовать нескольким вариантам (интервалам), то такой ряд будет иметь несколько значений моды.
При наличии одной моды распределение называют унимодальным,при двух модах – бимодальным,при трех и более модах – мультимодальным.
Отличие моды от средней выборочной заключается в том, она обладает определенной устойчивостью к изменению признака. Мода не изменяет своего значения при изменении крайних элементов ряда.
Еще одной важной порядковой средней является медиана.
Выборочной медианой (или просто медианой) называется одна из основных статистик распределения, которая характеризует середину вариационного (ранжированного) ряда.
Медиана – это значение, для которого 50% выборочных данных меньше этого значения, а 50% больше его, т.е. медиана делит вариационный ряд на две части, равные по числу вариантов.
Для дискретного вариационного ряда медиана равна серединному значению варианта, если объем совокупности является нечетным числом, или полусумме двух серединных вариантов, если объем совокупности является четным числом.
Пример 5.3. Найти медиану для дискретного вариационного ряда из примера 5.1:
Решение. Объем статистической совокупности равен n = 10 (четное число). Следовательно, медиана равна полусумме двух серединных вариантов х5 = 6 и х6 = 6, т.е. . ■
Пример 5.4. Найти медиану для дискретного вариационного ряда
Решение. Объем выборочной совокупности равен n = 9 (нечетное число). Следовательно, медиана равна серединному варианту х5, т.е. . ■
При нахождении медианы интервального ряда, вначале находят медианный интервал, т.е. интервал, содержащий медиану.
Медианному интервалу соответствует первая из накопленных частот, которая превышает половину объема выборочной совокупности. Внутри найденного интервала медиана рассчитывается по формуле:
,(5.7)
где ap – левая граница медианного интервала;
np – частота медианного интервала;
np-1нак – накопленная частота интервала, предшествующего медианному;
h – длина интервала.
Медиана, как и мода, может быть найдена графическим путем. Для этого используют кумулятивную кривую. Рассмотрим кумуляту распределения частот интервального ряда. Выделим на этой кумуляте отрезок, соответствующий медианному интервалу. Найдем на этом отрезке точку, ордината которой будет равна середине соответствующего интервала на оси ординат, как показано на следующем рисунке:
Тогда абсцисса найденной точки будет равна медиане рассматриваемого ряда.
Формула (5.7) получена из данного графического представления. Для ее вывода используются пропорциональность сторон в подобных треугольниках.
Иногда упрощают нахождение медианы, предполагая, что она приближенно равна середине медианного интервала.
Пример 5.5. Для интервального ряда из примера 5.2 аналитически и графически найти медиану и сравнить ее с серединой медианного интервала.
Решение.Дополним данный интервальный ряд строкой с накопленными частотами:
| Интервалы | 1 − 3 | 3 − 5 | 5 − 7 | 7 − 9 | 9 − 11 |
| Частоты интервалов | |||||
| niнак |
Половина объема совокупности равна 10, следовательно, медианным интервалом будет интервал [5 − 7], как первый интервал, для которого накопленная частота 16 превышает половину объема выборочной совокупности. Выпишем данные, необходимые для нахождения моды:
ap = 5; np = 7; np-1нак = 9; h = 7 – 5 = 2.
Подставляем данные в формулу (5.7), получаем
.
Середина медианного интервала равна z = 6, как видим, это достаточно грубое приближение для медианы. ■
Можно построить кумуляту и найти медиану графически.
Медиана, также как и мода, обладает определенным свойством устойчивости. На нее не влияет изменение крайних элементов вариационного ряда, если любой элемент, меньший медианы, остается также меньше ее, а любой больший медианы, будет также больше ее.
Одно из главных свойств медианы состоит в том, что сумма абсолютных величин отклонений вариантов от медианы меньше, чем от любой другой величины, в том числе и от средней выборочной.
Средние величины являются очень важными числовыми характеристиками вариационных рядов, однако, они не показывают изменчивость (вариацию) значений ряда. Перейдем к рассмотрению показателей вариации рядов.
Показатели вариации
Самым простым и самым приближенным показателем вариации (изменчивости) является, уже определенный выше, размах вариационного ряда. Напомним, что размах R равен разности между наибольшим и наименьшим значениями вариантов. Размах выборки – величина неустойчивая, существенно зависит от случайных обстоятельств, поэтому, по возможности, для решения практических задач не используется.
Более точными и более важными показателями вариации являются величины, которые характеризуют разброс значений вариант вокруг средней выборочной . К ним относятся: среднее линейное отклонение, дисперсия, среднеквадратическое отклонение и коэффициент вариации.
Среднее линейное (абсолютное) отклонение вариационного ряда – это характеристика изменчивости, равная средней арифметической абсолютных величин отклонений вариантов от их средней выборочной.
Для дискретного ряда распределения частот
| Варианты хi | x1 | x2 | … | xm |
| Частоты ni | n1 | n2 | … | nm |
среднее линейное отклонение находится по формуле:
(5.8)
Для интервального ряда формула для нахождения линейного отклонения почти такая же, только значения вариант в ней заменены серединами соответствующих интервалов, а именно
(5.9)
Следует обратить внимание, что если в формулах (5.8) и (5.9) в числителе не ставить знак модуля, то такая сумма отклонений всегда будет равна нулю и, следовательно, не может характеризовать разброс значений ряда.
Пример 5.6. Найти среднее линейное отклонение для дискретного ряда
Решение. Объем статистической совокупности равен n = 10. Найдем среднюю выборочную
.
Найдем по формуле (5.8) среднее линейное отклонение, получим
.■
В формуле для нахождения среднего линейного отклонения используется понятие модуля. Во многих задачах стараются не использовать это понятие, а заменять его каким-либо другим. В частности, такое нежелание использовать модуль, связано с тем, что функция не имеет производной в точке х = 0. При замене модуля используют следующий прием. Каждое отклонение берут не по модулю, а возводят в квадрат, чтобы избавиться от отрицательных знаков. Затем находят среднюю арифметическую полученных квадратов отклонений, т.е. величину, называемую дисперсией. Для определения самого среднего отклонения извлекают квадратный корень из дисперсии и получают величину, называемую среднеквадратическим отклонением.
Выборочной дисперсией вариационного ряда называется характеристика изменчивости, равная средней арифметической квадратов отклонений вариантов от их средней выборочной.
Для дискретного ряда распределения частот
| Варианты хi | x1 | x2 | … | xm |
| Частоты ni | n1 | n2 | … | nm |
дисперсия находится по формуле:
(5.10)
Для интервального ряда формула для нахождения дисперсии почти такая же, только варианты в ней заменены на середины соответствующих интервалов, а именно
(5.11).
Формула (5.10) может быть легко преобразована в следующую формулу
, (5.12)
где wi – частости интервалов.
Сравнив формулу (5.12) с формулой для нахождения дисперсии D(Х) дискретной случайной величины, видим внешнюю схожесть. Различие состоит в том, что в формулу (5.12) входит вместо математического ожидания средняя выборочная, а на месте вероятности поставлена частость.
Несмотря на эти различия, между теоретической и эмпирической дисперсиями много общего. Они обе являются мерой рассеивания. Кроме этого, как будет видно из дальнейшего, они обладают похожими свойствами. Поэтому, используя утверждения теорем Чебышева и Бернулли (см. параграф 1), можно считать дисперсию вариационного ряда при больших n приближенным значением или выборочным аналогом теоретической дисперсии, соответствующей случайной величины.
Выборочная дисперсия, также как и теоретическая, обладает одним существенным недостатком: она выражается в квадратных единицах значений вариантов. Таким образом, размерность вариантов и дисперсии не совпадает. Для того чтобы получить меру разброса значений в тех же единицах, что и значения вариантов, определяют еще одну характеристику изменчивости, называемую среднеквадратическим отклонением.
Среднеквадратическим отклонением вариационного ряда называется характеристика изменчивости, равная арифметическому квадратному корню из дисперсии, т.е.
(5.13)
Среднеквадратическое отклонение вариационного ряда называют эмпирическим или выборочным (а в некоторых учебниках и стандартным), чтобы показать его отличие от среднеквадратического отклонения (Х) случайной величины.
Пример 5.7. Найти среднеквадратическое отклонение для дискретного ряда из примера 5.6:
Решение. Объем статистической совокупности равен n = 10. При решении примера 5.6 была найдена средняя арифметическая . Применим формулу (5.12) и найдем дисперсию ряда, получим
.
Отсюда среднеквадратическое отклонение равно .■
Отметим основные свойства дисперсии и среднеквадратического отклонения, пояснение которых будем проводить на примере дискретного вариационного ряда:
1. Дисперсия и среднеквадратическое отклонение постоянной величины равны нулю.
Свойство становиться достаточно понятным, если вспомнить, что дисперсия определяет разброс значений, а постоянная величина разброса не имеет (или имеет разброс, равный нулю).
2. Если все варианты увеличить или уменьшить на одно и тоже число с, то дисперсия и среднее квадратическое отклонение не изменятся, т.е. и .
Доказательство следует из третьего свойства средней выборочной: с учетом следующих равенств:
.
3. Если все варианты увеличить (или уменьшить) в k раз, то дисперсия увеличиться (или уменьшиться) в k2 раз, а среднее квадратическое отклонение увеличиться (или уменьшиться) в |k|раз, т.е. и .
Доказательство также следует из третьего свойства средней выборочной: с учетом следующих равенств:
.
4. Если все частоты вариантов умножить на одно и тоже число, то дисперсия и среднеквадратическое отклонение не изменяться, а именно
5. Дисперсия вариационного ряда равна разности между средней арифметической квадратов вариантов и квадратом средней выборочной вариационного ряда, т.е. .
Доказательство получается из следующих равенств:
Для дисперсии существует определенное правило, которое имеет большое значение в статистическом анализе.
Дата добавления: 2016-11-12; просмотров: 3890 | Нарушение авторских прав | Изречения для студентов
Читайте также:
Рекомендуемый контект:
Поиск на сайте:
© 2015-2020 lektsii.org — Контакты — Последнее добавление
Вы́борочное
(эмпири́ческое) сре́днее —
это приближение теоретического среднего
распределения, основанное на выборке
из него.
Определение:
Пусть  —выборка из распределения
—выборка из распределения
вероятности,
определённая на некотором вероятностном
пространстве (Ω,F,P).
Тогда её выборочным средним
называется случайная
величина.

Свойства
выборочного среднего :
Пусть  —выборочная
—выборочная
функция распределения данной
выборки. Тогда для любого
фиксированного ω функция
функция 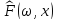 является
является
(неслучайной)функцией дискретного
распределения.
Тогда математическое
ожидание этого
распределения равно 
Выборочное
среднее — несмещённая
оценка теоретического
среднего:

Выборочное
среднее — сильно
состоятельная оценка теоретического
среднего:
 почти
почти
наверное при  .
.
Выборочное
среднее — асимптотически
нормальная оценка.
Пусть дисперсия случайных
величин 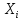 конечна
конечна
и ненулевая, то есть
Тогда  по
по
распределению при  ,
,
где  — нормальное
— нормальное
распределение со
средним 0 и
дисперсией  .
.
Выборочное
среднее из нормальной выборки — эффективная
оценка её
среднего
20. Выборочная дисперсия, её свойства.
Выборочная
дисперсия в математической
статистике —
это оценка теоретической дисперсии
распределения на основе выборки.
Различают выборочную дисперсию и
несмещённую, или исправленную, выборочные
дисперсии.
Определения
Пусть  —выборка из распределения
—выборка из распределения
вероятности.
Тогда
Выборочная
дисперсия — это случайная
величина
 ,
,
где
символ ![]() обозначаетвыборочное
обозначаетвыборочное
среднее.
Несмещённая
(исправленная) дисперсия — это случайная
величина
 .
.
Замечание
Очевидно,
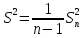 .
.
Свойства
выборочных дисперсий
Выборочная
дисперсия является
теоретической дисперсией выборочного
распределения.
Более точно, пусть 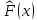 —выборочная
—выборочная
функция распределения данной
выборки. Тогда для любого фиксированного ω
функция  является
является
(неслучайной)функцией дискретного
распределения.
Дисперсия этого распределения равна  .
.
Обе
выборочные дисперсии являются состоятельными
оценками теоретической
дисперсии. Если ,

 И
И ,
,
где  обозначаетсходимость
обозначаетсходимость
по вероятности.
Выборочная
дисперсия является смещённой
оценкой теоретической
дисперсии, а исправленная выборочная
дисперсия несмещённой:
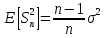 ,И
,И
Выборочная
дисперсия нормального
распределения имеет распределение
хи-квадрат.
Пусть ![]() .
.
Тогда
![]()
21. Статистические оценки: несмещенные, эффективные, состоятельные
Состоятельной
называют такую точечную статистическую
оценку, которая при n стрем к бесконечн
стремится по вероятности к оцениваемому
параметру. В частности, если дисперсия
несмещенной оценки при n стр к беск
стремится к нулю, то такая оценка
оказывается и состоятельной.
Рассмотрим
оценку θn числового
параметра θ, определенную при n =
1, 2, … Оценка θnназывается состоятельной,
если она сходится по вероятности к
значению оцениваемого параметра θ при
безграничном возрастании объема
выборки. Выразим сказанное более
подробно. Статистика θn является
состоятельной оценкой параметра θ
тогда и только тогда, когда для любого
положительного числа ε справедливо
предельное соотношение
![]()
Пример
3. Из закона
больших чисел следует, что θn = ![]() является
является
состоятельной оценкой θ =М(Х) (в
приведенной выше теореме Чебышёва
предполагалось существование
дисперсии D(X); однако,
как доказал А.Я. Хинчин [6], достаточно
выполнения более слабого условия –
существования математического
ожидания М(Х)).
Пример
4. Все
указанные выше оценки параметров
нормального распределения являются
состоятельными.
Вообще,
все (за редчайшими исключениями) оценки
параметров, используемые в
вероятностно-статистических методах
принятия решений, являются состоятельными.
Пример
5. Так, согласно
теореме В.И. Гливенко, эмпирическая
функция распределенияFn(x) является
состоятельной оценкой функции
распределения результатов наблюденийF(x)
Несмещенной
называют такую точечную статистическую
оценку Q*математическое
ожидание которой равно оцениваемому
параметру: M(Q*)=Q
Второе
важное свойство оценок – несмещенность.
Несмещенная оценка θn –
это оценка параметра θ, математическое
ожидание которой равно значению
оцениваемого параметра: М(θn)
= θ.
Пример
6. Из
приведенных выше результатов следует,
что ![]() и
и![]() являются
являются
несмещенными оценками
параметровm и σ2 нормального
распределения. Поскольку М(![]() )
)
= М(m**)
= m,
то выборочная медиана ![]() и
и
полусумма крайних членов вариационного
рядаm** —
также несмещенные оценки математического
ожидания mнормального
распределения. Однако
![]()
поэтому
оценки s2 и
(σ2)**
не являются состоятельными оценками
дисперсии σ2нормального
распределения.
Оценки,
для которых соотношение М(θn)
= θ неверно, называются смещенными. При
этом разность между математическим
ожиданием оценки θn и
оцениваемым параметром θ, т.е. М(θn)
– θ, называется смещением оценки.
Пример
7. Для
оценки s2,
как следует из сказанного выше, смещение
равно
М(s2)
— σ2 =
— σ2/n.
Смещение
оценки s2 стремится
к 0 при n →
∞.
Оценка,
для которой смещение стремится к 0,
когда объем выборки стремится к
бесконечности, называется асимптотически
несмещенной.
В примере 7 показано, что оценка s2 является
асимптотически несмещенной.
Практически
все оценки параметров, используемые в
вероятностно-статистических методах
принятия решений, являются либо
несмещенными, либо асимптотически
несмещенными. Для несмещенных оценок
показателем точности оценки служит
дисперсия – чем дисперсия меньше, тем
оценка лучше. Для смещенных оценок
показателем точности служит математическое
ожидание квадрата оценки М(θn –
θ)2.
Как следует из основных свойств
математического ожидания и дисперсии,
![]() (3)
(3)
т.е.
математическое ожидание квадрата
ошибки складывается из дисперсии оценки
и квадрата ее смещения.
Для
подавляющего большинства оценок
параметров, используемых в
вероятностно-статистических методах
принятия решений, дисперсия имеет
порядок 1/n,
а смещение – не более чем 1/n,
где n –
объем выборки. Для таких оценок при
больших n второе
слагаемое в правой части (3) пренебрежимо
мало по сравнению с первым, и для них
справедливо приближенное равенство
![]() (4)
(4)
где с –
число, определяемое методом вычисления
оценок θn и
истинным значением оцениваемого
параметра θ.
Эффективной
называют такую точечную статистическую
оценку, которая при фиксированном n
имеет наименьшую дисперсию.
С
дисперсией оценки связано третье важное
свойство метода оценивания –эффективность.
Эффективная оценка – это несмещенная
оценка, имеющая наименьшую дисперсию
из всех возможных несмещенных оценок
данного параметра.
Доказано
[11], что ![]() и
и![]() являются
являются
эффективными оценками
параметровm и σ2нормального
распределения. В то же время для
выборочной медианы ![]() справедливо
справедливо
предельное соотношение
![]()
Другими
словами, эффективность выборочной
медианы, т.е. отношение дисперсии
эффективной оценки ![]() параметраm к
параметраm к
дисперсии несмещенной оценки ![]() этого
этого
параметра при больших n близка к 0,637.
Именно из-за сравнительно низкой
эффективности выборочной медианы в
качестве оценки математического
ожидания нормального распределения
обычно используют выборочное среднее
арифметическое.
Понятие
эффективности вводится для несмещенных
оценок, для которых М(θn)
= θ для всех возможных значений параметра
θ. Если не требовать несмещенности, то
можно указать оценки, при некоторых θ
имеющие меньшую дисперсию и средний
квадрат ошибки, чем эффективные.
Пример
8. Рассмотрим
«оценку» математического ожидания m1 ≡
0. Тогда D(m1) =
0, т.е. всегда меньше дисперсии D(![]() )
)
эффективной оценки![]() .
.
Математическое ожидание среднего
квадрата ошибкиdn(m1)
= m2,
т.е. при ![]() имеемdn(m1)
имеемdn(m1)
< dn(![]() ).
).
Ясно, однако, что статистикуm1 ≡
0 бессмысленно рассматривать в качестве
оценки математического ожидания m.
Пример
9. Более
интересный пример рассмотрен американским
математиком Дж. Ходжесом:
![]()
Ясно,
что Tn –
состоятельная, асимптотически несмещенная
оценка математического ожидания m,
при этом, как нетрудно вычислить,
![]()
Последняя
формула показывает, что при m ≠
0 оценка Tn не
хуже ![]() (при
(при
сравнении по среднему квадрату
ошибки dn),
а при m =
0 – в четыре раза лучше.
Подавляющее
большинство оценок θn,
используемых в вероятностно-статистических
методах, являются асимптотически
нормальными, т.е. для них справедливы
предельные соотношения:
![]()
для
любого х,
где Ф(х) –
функция стандартного нормального
распределения с математическим ожиданием
0 и дисперсией 1. Это означает, что для
больших объемов выборок (практически
— несколько десятков или сотен наблюдений)
распределения оценок полностью
описываются их математическими
ожиданиями и дисперсиями, а качество
оценок – значениями средних квадратов
ошибок dn(θn).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
