Какими свойствами обладает сумма произведение частное рациональных чисел
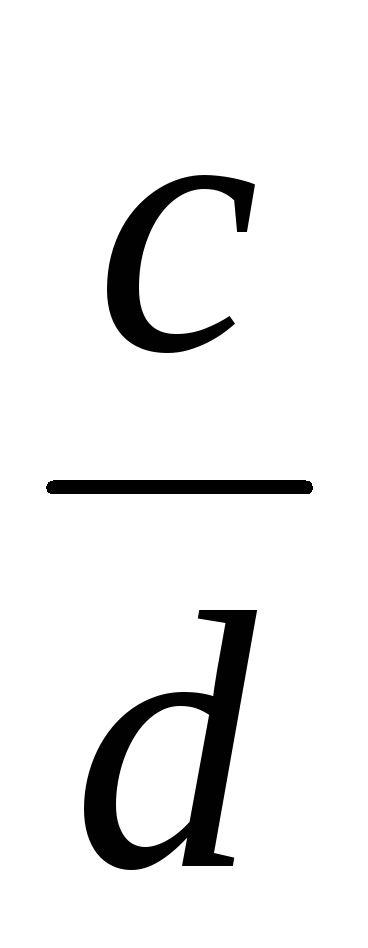
1. Сложение рациональных чисел обладает переместительным и сочетательным свойствами.
Иными словами, если a, b и с — любые рациональные числа, то а + b = b + a, а+(b + с) = (а + b) + с.
Прибавление нуля не изменяет числа, а сумма противоположных чисел равна нулю.
Значит, для любого рационального числа имеем: а + 0 = а, а + ( — а)=0.
Умножение рациональных чисел тоже обладает переместительным и сочетательным свойствами. Другими словами, если а, b и с — любые рациональные числа, то ab — ba, a(bc) — (ab)c.
Умножение на 1 не изменяет рационального числа, а произведение числа на обратное ему число равно 1.
Значит, для любого рационального числа а имеем:
Умножение числа на нуль дает в произведении нуль, т. е. для любого рационального числа а имеем:
а • 0 = 0.
Произведение может быть равно нулю лишь в том случае, когда хотя бы один из множителей равен нулю: если а • b = 0, то либо а = 0, либо b = 0 (может случиться, что и а = 0, и b=0).
Умножение рациональных чисел обладает и распределительным свойством относительно сложения. Другими словами, для любых рациональных чисел a, b и с имеем: (a+b)• c = ac+bc.
С рациональными числами люди, как вы знаете, знакомились постепенно. Вначале при счете предметов возникли натуральные числа. На первых порах их было немного. Так, еще недавно у туземцев островов в Торресовом проливе (отделяющем Новую Гвинею от Австралии) были в языке названия только двух чисел: «урапун» (один) и «оказа» (два). Островитяне считали так: «оказа-урапун» (три), «оказа-оказа» (четыре) и т. д. Все числа, начиная с семи, туземцы называли словом, обозначавшим «много».
Ученые полагают, что слово для обозначения сотни появилось более 7000 лет назад, для обозначения тысячи — 6000 лет назад, а 5000 лет тому назад в Древнем Египте и в Древнем Вавилоне появляются названия для громадных чисел — до миллиона. Но долгое время натуральный ряд чисел считался конечным: люди думали, что существует самое большое число.
Величайший древнегреческий математик и физик Архимед (287—212 гг. до н. э.) придумал способ описания громадных чисел. Самое большое число, которое умел называть Архимед, было настолько велико, что для его цифровой записи понадобилась бы лента в две тысячи раз длиннее, чем расстояние от Земли до Солнца.
Но записывать такие громадные числа еще не умели. Это стало возможным только после того, как индийскими математиками в VI в. была придумана цифра нуль и ею стали обозначать отсутствие единиц в разрядах десятичной записи числа.
При разделе добычи и в дальнейшем при измерениях величин, да и в других похожих случаях люди встретились с необходимостью ввести «ломаные числа» — обыкновенные дроби. Действия над дробями еще в средние века считались самой сложной областью математики. До сих пор немцы говорят про человека, попавшего в затруднительное положение, что он «попал в дроби».
Чтобы облегчить действия с дробями, были придуманы десятичные дроби. В Европе их ввел в Х585 г. голландский математик и инженер Симон Стевин.
Отрицательные числа появились позднее, чем дроби. Долгое время такие числа считали «несуществующими», «ложными» прежде всего из-за того, что принятое истолкование для положительных и отрицательных чисел «имущество — долг» приводило к недоумениям: можно сложить или вычесть «имущества» или «долги», но как понимать произведение или частное «имущества» и «долга»?
Однако несмотря на такие сомнения и недоумения, правила умножения и деления положительных и отрицательных чисел были предложены в III в. греческим математиком Диофантом (в виде: «Вычитаемое, умноженное на прибавляемое, дает вычитаемое; вычитаемое на вычитаемое дает прибавляемое» и т. д.), а позже индийский математик Б х а с к а р а (XII в.) выразил те же правила в понятиях «имущество», «долг» («Произведение двух имуществ или двух долгов есть имущество; произведение имущества и долга есть долг». То же правило и при делении).
Было установлено, что свойства действий над отрицательными числами те же, что и над положительными (например, сложение и умножение обладают переместительным свойством). И наконец с начала прошлого века отрицательные числа стали равоправными с положительными.
В дальнейшем в математике появились новые числа — иррациональные, комплексные и другие. О них вы узнаете в старших классах.
Отношение равенства является отношением эквивалентности на множестве дробей, поэтому оно порождает на нём классы эквивалентности. В каждом таком классе содержатся равное между собой дроби. Например, множество дробей {, , , , …} – это один класс, множество дробей {, , , , …} – это другой класс и т.д.
Дроби одного класса выражают длину одного и того же отрезка. Но длина отрезка должна представляться единственным числом. Поэтому считают, что равные дроби – это различные записи одного и того же положительного рационального числа.
Положительным рациональным числом называется класс дробей, а каждая дробь, принадлежащая этому классу, есть запись (представление) этого числа.
Например, о дроби мы должны говорить, что она является записью некоторого рационального числа. Однако часто для краткости говорят: – это рациональное число.
Множество всех положительных рациональных чисел принято обозначать символом Q+. Определим на это множество отношение равенства.
Если положительное рациональное число a представить дробью , а положительное рациональное число b – другой дробью , то a = b тогда и только тогда, когда mq=np.
Из данного определения следует, что равные рациональные числа представляются равными дробями. Среди всех записей любого положительного рационального числа выделяют дробь, которая является несократимой, и доказывают, что любое рациональное число представимо единственным образом несократимой дробью (мы это доказательство опускаем). Для того чтобы рациональное число представить несократимой дробью, достаточно числитель m и знаменатель n разделить на их наибольший общий делитель.
Выяснить теперь, как определяются арифметические действия с положительными рациональными числами.
Пусть при некотором единственном отрезке e длина отрезка x выражается дробью , а длина отрезка у – дробью , и пусть отрезок z состоит из отрезков x и y. Такая n-ая часть отрезка e укладывается в отрезок z m+p раз, т.е. длина отрезка z выражается дробью . Поэтому полагают, что .
Если положительное рациональное число a представить дробью , а положительное рациональное число b – дробью , то их суммой называется число a+b, которое представляется дробью .
Таким образом по определению
. (1)
Можно доказать, что при замене дробей и , представляющих числа а и b, равными им дробями, дробь заменяется равной ей дробью. Поэтому сумма рациональных чисел не зависит от выбора представляющих их дробей.
В определении суммы рациональных чисел мы использовали их представления в виде дробей с одинаковыми знаменателями. Если же числа а и b представлены дробями с различными знаменателями, то сначала надо привести их к одному знаменателю, а затем применить правило (1).
Сложение положительных рациональных чисел коммутативно и ассоциативно,
( Q+) a + b = b + a;
( Q+) (a + b) + c = a + (b + c).
Докажем, например, коммутативность сложения. Представим числа а и b дробями и . Тогда сумма a+b представляется дробью , а сумма b+a – дробью . Так как m, p, n – натуральные числа, то m+p = p+m и, следовательно, a+b = b+a. Таким образом, коммутативность сложения положительных рациональных чисел вытекает из коммутативности сложения натуральных чисел.
Если положительное числа а представлено дробью , а положительное рациональное число b – дробью , то их произведением называется число ab, которое представляет дробью .
Такимобразом, по определению,
. (2)
Можно доказать, что при замене дробей и , представляющих числа a и b, равными им дробями, дробь заменяется равной ей дробью. Поэтому произведение чисел a и b не зависит от выбора представляющих их дробей.
Умножение положительных рациональных чисел коммутативно, ассоциативно и дистрибутивно относительно сложения и вычитания. Доказательство этих свойств основывается на определении умножения исложения положительных рациональных чисел, а также на соответствующих свойствах сложения и умножения натуральных чисел.
Определение сложения положительных рациональных чисел дает возможность определить отношение «меньше» на множестве Q+.
Пусть a и b — положительные рациональные числа. Считают, что число b меньше числа а, если существует такое положительное рациональное число с, что а =b + с.
В этом же случае считают, что число а больше числа b. Пишут b < a,
a >b.
Так определенное отношение «меньше» обладает рядом свойств, которые мы приводим без доказательства.
1. Отношение «меньше» на множестве Q+ антисимметрично и транзитивно, т.е. является отношением порядка, а множество Q+ упорядоченным множеством.
2. Если рациональные числа a и b представлены дробями и (т.е. дробями, имеющими одинаковые знаменатели), то a <b в том и только в том случае, когда m < p.
3. Если рациональные числа aи bпредставлены дробями и (т.е. дробями, имеющими разные знаменатели), то a < b в том и только в том случае, когда mq < пр.
4. Во множестве положительных рациональных чисел нет наименьшего числа.
5. Между любыми двумя различными числами а и b из Q+ заключено бесконечно много чисел этого же множества. Это свойство называют свойством плотности множества Q+.
6. Во множестве положительных рациональных чисел нет наибольшего числа.
Вычитание положительных рациональных чисел определяется как операция, обратная сложению, т.е. это такая операция, которая удовлетворяет условию: a – b = c тогда и только тогда, когда a = b + c.
Разность а — b положительных рациональных чисел существует тогда и только тогда, когда b < а. Если разность а — b существует, то она единственна.
Используя определение и условие существования разности, можно получить правило вычитания положительных рациональных чисел, представленных дробями и , где т < р:
(3)
Деление положительных рациональных чисел определяется как операция, обратная умножению, т.е. это такая операция, которая удовлетворяет условию: тогда и только тогда, когда .
Из этого определения и правила нахождения произведения положительных рациональных чисел можно получить правило деления положительных рациональных чисел, представленных дробями и :
. (4)
Из этого правила следует, что частное положительных рациональных чисел всегда существует.
Определим
во множестве Q
операции сложения, умножения, и их
свойства.
1.
Сравнение.
Пусть
даны два рациональных числа K(![]() )
)
и K(![]() ).
).
Определение:
Два рациональных числа называются
равными,
если они представлены эквивалентными
дробями.
Другими
словамиK(![]() )
)
= K(![]() )
)
![]() ad
ad
= bc
Определение:
Суммой
двух рациональных чисел K(![]() )
)
и K(![]() )
)
называется рациональное число K(![]() ).
).
Таким
образом,K(![]() )
)
+ K(![]() )
)
= K(![]() )
)
Теорема:
Сумма двух рациональных чисел K(![]() )
)
и K(![]() )
)
не зависят от выбора их представителей.
Доказательство:
Пусть
даны два рациональных числа K(![]() )
)
и K(![]() ),
),
их сумма определяется рациональным
числом K(![]() ).
).
Пусть
![]()
![]() K(
K(![]() )
)
и
![]()
![]() K(
K(![]() ),
),
их сумма по определению определяется
K(![]() ).
).
Покажем, что K(![]() )
)
+ K(![]() )
)
= K(![]() )
)
+ K(![]() ),
),
а для этого нужно показать, что
![]()
~![]() .
.
Доказательство:
Т ак
ак
как![]()
![]() K(
K(![]() )
)![]()
![]()
~
![]()
![]() a‘b
a‘b
= b‘a
Умножим обе части равенства на dd‘.
Так
как
![]()
![]() K(
K(![]() )
)![]()
![]()
~
![]()
![]() c‘d
c‘d
= d‘c
Умножим обе части равенства на bb‘.
a‘bdd‘
= b‘add‘
+
c‘dbb‘
= d‘cbb‘
a‘bdd‘
+ c‘dbb‘
= b‘add‘
+ d‘cbb‘
 bd(a’d
bd(a’d![]() +
+
b’c’) = b’d'(ad + bc)
Это
равенство означает, что
![]()
~
![]() ,
,
то есть
![]()
![]() K(
K(![]() ).
).
Определение:
Произведением
двух рациональных чисел K(![]() )и
)и
K(![]() )
)
называется рациональное число K(![]() ).
).
Таким
образом, K(![]() )
)
* K(![]() )
)
= K(![]() ).
).
Теорема:
Произведение двух рациональных чисел
K(![]() )
)
и K(![]() )
)
не зависит от выбора их представителей.
Дано:
K(![]() );
);
K(![]() )
)
– рациональные числа, K(![]() )
)
* K(![]() )
)
= K(![]() ).
).
Пусть![]()
![]() K(
K(![]() )
)
и
![]()
![]() K(
K(![]() ),
),
тогда K(![]() )
)
* K(![]() )
)
= K(![]() ).
).
Доказать:
K(![]() )
)
= K(![]() ),
),
то есть
![]() ~
~![]() .
.
Доказательство:
Так
как
![]()
![]() K(
K(![]() ),
),
то
![]()
~
![]() a‘b
a‘b
= b‘a
так
как
![]()
![]() K(
K(![]() ),
),
то![]()
~![]() c‘d
c‘d
= d‘c
Перемножим
почленно эти равенства: a‘bc‘d=b‘ad‘c
или (ac)(b‘d‘)=(bd)(a‘c‘).
Это равенство означает, что
![]() ~
~![]() ,
,
то есть
![]()
![]() K(
K(![]() ).
).
Определение:
Разностью
двух рациональных чисел K(![]() )и
)и
K(![]() )называется
)называется
рациональное число K(![]() ),
),
которое удовлетворяет равенству:
K(![]() )
)
+ K(![]() )
)
= K(![]() ).
).
Теорема:
Разность любых двух рациональных чисел
существует и единственна.
Доказательство:
I.
Существование.
а)
Найдем вид числа K(![]() ).
).
По определению разности оно удовлетворяет
условию:
K(![]() )
)
+ K(![]() )
)
= K(![]() ).
).
По
определению суммы K(![]() )
)
+ K(![]() )
)
= K(![]() )K(
)K(![]() )
)
= K(![]()
).
Но
два рациональных числа равны, если
![]()
~![]() ,
,
то есть если
ady
= b(cy
+ dx).
Тогда, ady
= bcy
+ bdxady
— bcy
= bdx
![]() y(ad
y(ad
– bc)
= bdx
![]() ~
~
![]() K(
K(![]() )
)
= K(![]()
).
б)
Покажем, что найденное рациональное
число является разностью чисел K(![]() )
)
и K(![]() ).
).
Проверим
выполнимость равенства: K(![]() )
)
+ K(![]() )
)
= K(![]() ).
).
K(![]() )
)
+ K(![]() )
)
= K(![]() )
)
= K(![]() )
)
= K(![]() )
)
= K(![]() ),
),
так как![]() ~
~![]()
.
Итак,
существование разности доказано. Докажем
ее единственность.
II.
Единственность
разности.
Предположим,
что существует две разности рациональных
чисел K(![]() )
)
и K(![]() ),
),
то есть K(![]() )
)
– K(![]() )
)
= K(![]() )
)
и (1) K(![]() )
)
– K(![]() )
)
= K(![]() )
)
(2)
Покажем,
что K(![]() )
)
= K(![]() ).
).
Из
(1) следует, что K(![]() )
)
= K(![]() )
)
+ K(![]() );
);
из (2) следует, что K(![]() )
)
= K(![]() )
)
+ K(![]() ).
).
Тогда K(![]() )
)
+ K(![]() )
)
= K(![]() )
)
+ K(![]() ).
).
По
определению суммы имеем: K(![]() )
)
= K(![]() ),
),
что возможно, если
![]() ~
~![]() .Тогда
.Тогда
по определению равносильных дробей
имеем:
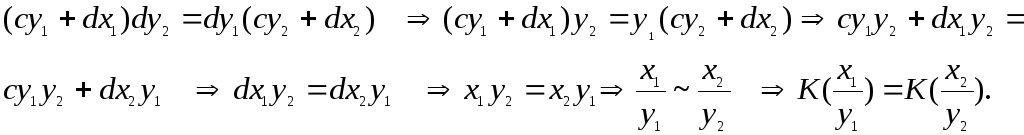
Определение:
Частным
от деления рационального числа K(![]() )
)
на рациональное число K(![]() )
)
≠ 0,
называется рациональное число K(![]() ),
),
удовлетворяющее уравнению:
K(![]() )
)
* K(![]() )
)
= K(![]() )
)
В
дальнейшем будем использовать обозначение:
K(![]() )
)
: K(![]() )
)
= K(![]() )
)
Теорема:
Частное
от деления любого рационального числа
K(![]() )
)
на рациональное число K(![]() )≠
)≠
существует и единственно.
Доказательство:
I.
Существование.
а)
Определим вид частного двух рациональных
чисел.
По
определению K(![]() )
)
: K(![]() )
)
= K(![]() )
)
![]() K(
K(![]() )
)
* K(![]() )
)
= K(![]() ).
).
K(![]() )
)
* K(![]() )
)
= K(![]() )K(
)K(![]() )
)
= K(![]() )
)
![]()
~
![]() cxb
cxb
= dya
или xbc
=yad,
это означает, что
![]()
~
![]() ,
,
то есть K(![]() )
)
= K(![]() ).Таким
).Таким
образом, вид частного определили.
б)
покажем, что это число является частным
от деления рационального числа K(![]() )
)
на K(![]() ).
).
Тогда должно выполняться равенство:
K(![]() )
)
* K(![]() )
)
= K(![]() ).
).
K(![]() )
)
* K(![]() )
)
= K(![]() )
)
= K(![]() ),
),
так как![]()
~
![]() .
.
Итак,
существование доказано.
II.
Единственность.
Пусть
существуют два частных K(![]() )
)
и K(![]() )
)
от деления рационального числа K(![]() )
)
на K(![]() )
)
≠ 0.
Тогда выполняются равенства:
 K(
K(![]() )
)
* K(![]() )
)
= K(![]() )(1)K(
)(1)K(![]() )
)
= K(![]() )
)
![]()
![]()
K(![]() )
)
* K(![]() )
)
= K(![]() )
)
(2) K(![]() )
)
= K(![]() )
)
K(![]() )
)
= K(![]() )
)
![]()
![]()
~
![]()
![]()
![]()
![]()
![]()
~
![]()
![]() K(
K(![]() )
)
= K(![]() ).
).
Следствие:
Частное рациональных чисел находится
по формуле:
K(![]() )
)
: K(![]() )
)
= K(![]() ).
).
Замечание:
Операции сложения, умножения и деления
на множестве
![]() (положительных рациональных чисел)
(положительных рациональных чисел)
определяется так же, как и наQ.
Операция вычитания на
![]() существует не всегда.
существует не всегда.
Теорема:
Для того, чтобы разность положительных
рациональных чисел a
и bсуществовала
необходимо и достаточно, чтобы b
< a.
(доказательство
аналогично теореме на N)
Теорема:
Сумма и произведение положительных
рациональных чисел являются положительными
рациональными числами.
Пусть
рациональное число K(![]() )
)
задается дробью
![]() ;
;
K(![]() )
)
задается дробью
![]() .
.
1.
Так как K(![]() )
)
положительное, то a
> 0 и b
> 0
![]()
(1) ab
> 0.
Аналогично cd
> 0 (2).
Умножим (1) на d²
>0,
а
(2) на b² >0
abd²
>0 и cdb² >0
сложим их: abd²
+ cdb²
>0 (ad+cb)bd
>0 . Тогда
![]() >0
>0
, но
![]()
=![]() +
+![]()
![]()
![]() +
+![]() >0,
>0,
ч.т.д.
2.
Если ab>0
и cd>0 , то (ab)(cd)>0
![]() (ac)(bd)>0
(ac)(bd)>0
![]() *
*![]() >0,
>0,
ч.т.д.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ
