Какими свойствами обладает статический момент
Меню сайта
Расчет геометрических характеристик сечений он-лайн NEW — считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.
Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной
сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн.
+ Полное расписанное решение!
Теперь и для статически неопределимых балок!
Расчет рам, ферм балок он-лайн NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы.
Лекции — теория, практика, задачи…
Примеры решения задач
Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое.
Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое).
Форум сопромата и механики
Книги — разная литература по теме.
Заказать задачу
Друзья сайта (ссылки)
WIKIbetta
Разработчикам (сотрудничество)
Веб-мастерам (партнёрка)
О проекте, контакты
Подпроекты
Базовый курс лекций по сопромату, теория, практика, задачи.
::Оглавление::
:: Посмотреть новый вариант этой лекции::
:: Пример расчета ::
:: Расчет характеристик он-лайн (программа) ::
1. Геометрические характеристики сечений.
1.1. Статический момент сечения.
При дальнейшем изучении вопросов прочности, жесткости и устойчивости нам придется иметь дело с некоторыми геометрическими характеристиками сечения: статическими моментами, моментами инерции, моментами сопротивления.
Статическим моментом Sx сечения (фигуры) относительно какой-либо оси х (рис.1.1) называется геометрическая характеристика, определяемая интегралом вида
(1.1)
где y — расстояние от элементарной площадки dA до оси x.
Единицей измерения статического момента является единица длины в третьей степени, обычно см3(см в третьей степени). Статический момент может быть положительным, отрицательным и, в частности, равным нулю. Если отождествить площадь с силой, действующей перпендикулярно плоскости чертежа, то интеграл (4.1) можно рассматривать как сумму моментов сил относительно оси х. По известной из теоретической механике теореме о моменте равнодействующей можно написать
(1.2)
где А — площадь всей фигуры (равнодействующая); ус — расстояние от центра тяжести фигуры до оси х.
Из формулы (1.2) следует формула определения ординаты центра тяжести
ус = Sx/A. (1.3)
Аналогично, статический момент относительно оси у равен
(1.4)
Откуда
xс = Sy/A. (1.5)
Центр тяжести обладает тем свойством, что если тело опереть в этой точке, то оно будет находиться в равновесии.
Из формулы (1.2) и (1.4) следует, что если оси х и у проходят через центр тяжести фигуры, то статический момент относительно этих осей равен нулю. Такие оси называются центральными осями.
Если фигуру можно представить в виде отдельных простых фигур (квадратов, треугольников и т.д.), для которых известны положения центров тяжести, то в этом случае статический момент всей фигуры можно получить как сумму статических моментов этих простых фигурю Это непостредственно следует из свойств определенного интеграла.
Если фигура имеент ось симметрии, то последняя всегда проходит через центр тяжести фигуры, а потому статический момент фигуры относительно оси симметрии всегда равен нулю.
Во многих случаях вместо простых интегралов вида (1.1) и (1.4) удобнее иметь дело с двойными интегралами вида:
(1.1a)
(1.4a)
Здесь D — облать интегрирования.
Пример 1.1. Определить положение центра тяжести сечения, показанного на рис. 1.2, а.
Решение. Разбиваем сечение на два прямоугольника. Проводим вспомогательные оси х и у.
По формулам (1.3) и (1.5) получим:
По этим координатам находим точку С — центр тяести сечения. Она лежит на линии, соединяющей точки С1 и С2, ближе к фигуре, имеющей большую площадь.
Пример 1.2. Вычислить ординату центра тяжести половины круга (рис. 1.2, б).
Решение. Пользуемся формулой
Вычисляем числитель, используя уравнение окружности х2 + y2 = R2:
Вычисляем ус
Полезные ссылки
1. Пример расчета геометрических характеристик
2. Расчет характеристик он-лайн (программа)
::Оглавление::
Сообщество
Вход
Решение задач
Расчет редукторов
Для Android (рекомендую)
NEW Mobile Beam 2.0
Программа для расчета балок на прочность на Вашем Android устройстве…
Java 2 ME
Макеты страниц
Статическим моментом сечения относительно некоторой оси называется взятая по всей его площади F сумма произведений элементарных площадок на их расстояния от этой оси, т. е.
Статические моменты выражаются в и т. д.
Для сложного сечения, состоящего из частей, выражения (2.5) можно представить в виде
где — статические моменты части сечения относительно осей и у соответственно.
Итак, статический момент сложного сечения относительно некоторой оси равен сумме статических моментов всех частей этого сечения относительно той же оси.
Нельзя суммировать статические моменты частей сечения, вычисленные относительно различных осей.
Рис. 2.5
Рис. 3.5
Рассмотрим сечение, показанное на рис. 2.5. Очевидно, что статический момент части сечения, расположенной выше оси 2, положителен, так как для любой площадки этой части ординаты у положительны; для части же сечения, расположенной оси , статический момент отрицателен и меньше по абсолютной величине. Поэтому статический момент всего рассматриваемого сечения положителен.
Если за положительное для оси у выбрать направление вниз (а не вверх, как на рис. 2.5), то интеграл станет отрицательным, а интеграл — положительным; статический момент всего сечения, равный сумме этих интегралов, станет отрицательным.
Таким образом, изменение положительного направления оси у вызывает изменение знака статического момента аналогично изменение положительного направления оси вызывает изменение знака статического момента
Рис. 4.5
Рис. 5.5
Установим зависимость между статическими моментами одного и того же сечения относительно двух параллельных друг другу осей (рис. 3.5). Выражения статических моментов относи тельно этих осей на основании (2.5) имеют вид
но
и, следовательно,
Окончательно
и аналогично
Найдем теперь положение осей , и (рис. 4.5), относительно которых статические моменты равны нулю. Для этого приравняем нулю выражения (4.5) и (5.5):
откуда
Точка пересечения таких осей (точка С на рис. 4.5) называется центром тяжести сечения, а оси, проходящие через центр тяжести, — центральными осями. Относительно любой оси, проходящей через центр тяжести сечения (т. е. относительно любой центральной оси), статический момент равен нулю.
Формулы (6.5) используются для определения координат центра тяжести сечения.
Для случаев, когда положение центра тяжести сечения известно, а требуется определить статические моменты сечения относительно любых осей у и z (рис. 5.5), формулы (6.5) преобразуются к виду
Определим для примера положение центра тяжести сечения, показанного на рис. 6.5. Для этого разобьем сечение на две части: прямоугольник площадью и квадрат площадью Центры тяжести этих частей показаны на рис. 6.5.
Рис. 6.5
Проведем случайные оси у и . Вычислим статический момент сечения относительно оси :
В этом выражении — статические моменты частей сечения площадями относительно оси , равные [на основании выражения (7.5)]:
Следовательно,
и на основании выражения (6.5)
где
Аналогично
где
Следовательно,
По найденным значениям координат на рис. 6.5 установлено положение центра тяжести С заданного сечения.
Положение центра тяжести того же сечения (см. рис. 6.5) можно найти более просто, если случайные оси провести через центр тяжести одной из частей, на которые разбито сечение.
Рис. 7.5
Рис. 8.5
Будем, например, рассматривать площадь заданного сечения как разность площадей квадрата квадрата 2, 5, 6, 7, так как заданное сечение можно получить путем вычитания квадрата из квадрата (рис. 7.5). Тогда относительно осей у и z, показанных на рис. 7.5:
(здесь так как ось 2 проходит через центр тяжести квадрата
Найденное положение центра тяжести С заданного сечения показано на рис. 7,5; оно совпадает с полученным выше (см. рис. 6.5).
Заметим, что разбивку сечения на составные части несколькими способами или выбор различных координатных систем (или то и другое) надо широко использовать для контроля правильности определения положения центра тяжести.
Следует иметь в виду, что при вычислении статических моментов сечений необходимо учитывать знаки координат центров тяжести отдельных частей фигуры. Так, например, при вычислении статического момента сечения (рис. 8.5) относительно оси абсциссу следует взять со знаком «минус»:
На основании рассмотренных примеров можно установить следующий порядок определения положения центра тяжести сложного сечения.
1. Сложное сечение разбивается на части, имеющие вид простых фигур.
2. Определяются площади и положения центров тяжести каждой фигуры.
3. Выбираются случайные координатные оси у и 2.
4. По формулам (7.5) вычисляются статические моменты каждой фигуры относительно осей у и . Затем путем суммирования значений [в соответствии с выражениями (3.5)] определяется статический момент а значений — статический момент всего сечения.
5. По формулам (6.5) вычисляются координаты центра тяжести всего сечения.
В отдельных случаях, когда заданное сечение нельзя разбить на такие фигуры, положения центров тяжести которых известны, положение центра тяжести всего сечения необходимо определять путем непосредственного интегрирования. Такие случаи рассмотрены в примере 1.5.
Меню сайта
Расчет геометрических характеристик сечений он-лайн NEW — считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.
Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной
сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн.
+ Полное расписанное решение!
Теперь и для статически неопределимых балок!
Расчет рам, ферм балок он-лайн NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы.
Лекции — теория, практика, задачи…
Примеры решения задач
Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое.
Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое).
Форум сопромата и механики
Книги — разная литература по теме.
Заказать задачу
Друзья сайта (ссылки)
WIKIbetta
Разработчикам (сотрудничество)
Веб-мастерам (партнёрка)
О проекте, контакты
Подпроекты
Базовый курс лекций по сопромату, теория, практика, задачи.
::Оглавление::
1. Геометрические характеристики сечений
1.1. Статический момент сечения
Статические моменты сечения Sx и Sy используются главным образом для определения положения центра площади сечения и центральных осей.
Рассмотрим изменение статических моментов при параллельном переносе осей (рис. 1.1). Считая известными F, Sx и Sy в системе координат 0XY определим статические моменты Sx1, Sy1 относительно новых осей x1, y1.
Рис. 1.1
Учитывая соотношения x1 = x — a и y1 = y — b получим:
или
Sx1 = Sx — bF; Sy1 = Sy — aF; (1.1)
Оси x1, y1 можно выбрать таким образом, чтобы выполнились условия:
Sx1 = 0, Sy1 = 0.
Оси, относительно которых статические моменты сечения равны нулю, называются центральнми. Точка пересечения центральных осей называется центром тяжести сечения.
Принимая Sx1 = 0 и Sy1 = 0, из выражения (1.1) координаты центра площади сечения относительно вспомогательных осей x, y определяются по формулам (обозначим xc = a, yc = b):
| (1.2) |
Соответственно, если площадь F и положение центра площади сечения (координаты xc, yc) в системе координат 0xy известны, то статические моменты сечения относительно осей x, y можно определить из выражений (1.2):
Sx = F yc; Sy = F xc. (1.3)
Можно показать, что статический момент относительно любой оси, проходящей через центр площади сечения, равен нулю.
При определении центра площади сложного сечения применяется следующая процедура:
1) сечение разбивается на n частей, площади (Fi) и положение центров (Ci) площади которых известны;
2) задается вспомогательная система координат, в которой определяются координаты центров площадей (xci, yci) этих частей;
3) вычисляются координаты составного сечения по формулам:
| (1.4) |
Примеры
Пример 1. Выполнен с помощью он-лайн программы. (перейдя к примеру нажмите на одно из действий в блоке-меню «Расчет»)
::Старый вариант этой лекции::
::Оглавление::
Сообщество
Вход
Решение задач
Расчет редукторов
Для Android (рекомендую)
NEW Mobile Beam 2.0
Программа для расчета балок на прочность на Вашем Android устройстве…
Java 2 ME
Известны
три геометрические характеристики –
это длина, площадь, объем, которые имеют
определенный физический смысл. Рассмотрим
новые характеристики, которые будут
использоваться в расчетных формулах
сопротивления материалов: статические
моменты и моменты инерции площадей
сечений. Эти характеристики не имеют
прямого физического смысла. Их нельзя
измерить привычным путем. При выводе
формул сопротивления материалов иногда
случается, что их часть представляет
собой интегральное выражение, зависящее
только от формы и размеров сечения. Для
упрощения последующего использования
этих формул удобно такое выражение
подсчитать заранее для различных форм
сечений.
Статические
моменты площади сечений используются
при определении положения центра тяжести
сечения, при расчете касательных
напряжений при изгибе.
Моменты
инерции используются при расчете
напряжений и перемещений при изгибе,
кручении и т. д.
3.1. Статические моменты площади сечений
Статическими
моментами площади сечения называются
интегралы следующего вида:
![]() ,
,
![]()
В
целях их геометрической интерпретации
рассмотрим сечение произвольной формы
(рис. 3). Выделим в сечении элементарную
площадку dA
с координатами
y
и z.
Произведение
площади dA
на координату
y
есть элементарный
статический момент dSz
относительно
оси z.
Это понятие
аналогично моменту силы относительно
оси. Если предположить, что А
– это вес
пластины, имеющей форму нашего сечения,
то статический момент Sz
– это момент
силы тяжести пластины относительно оси
z.
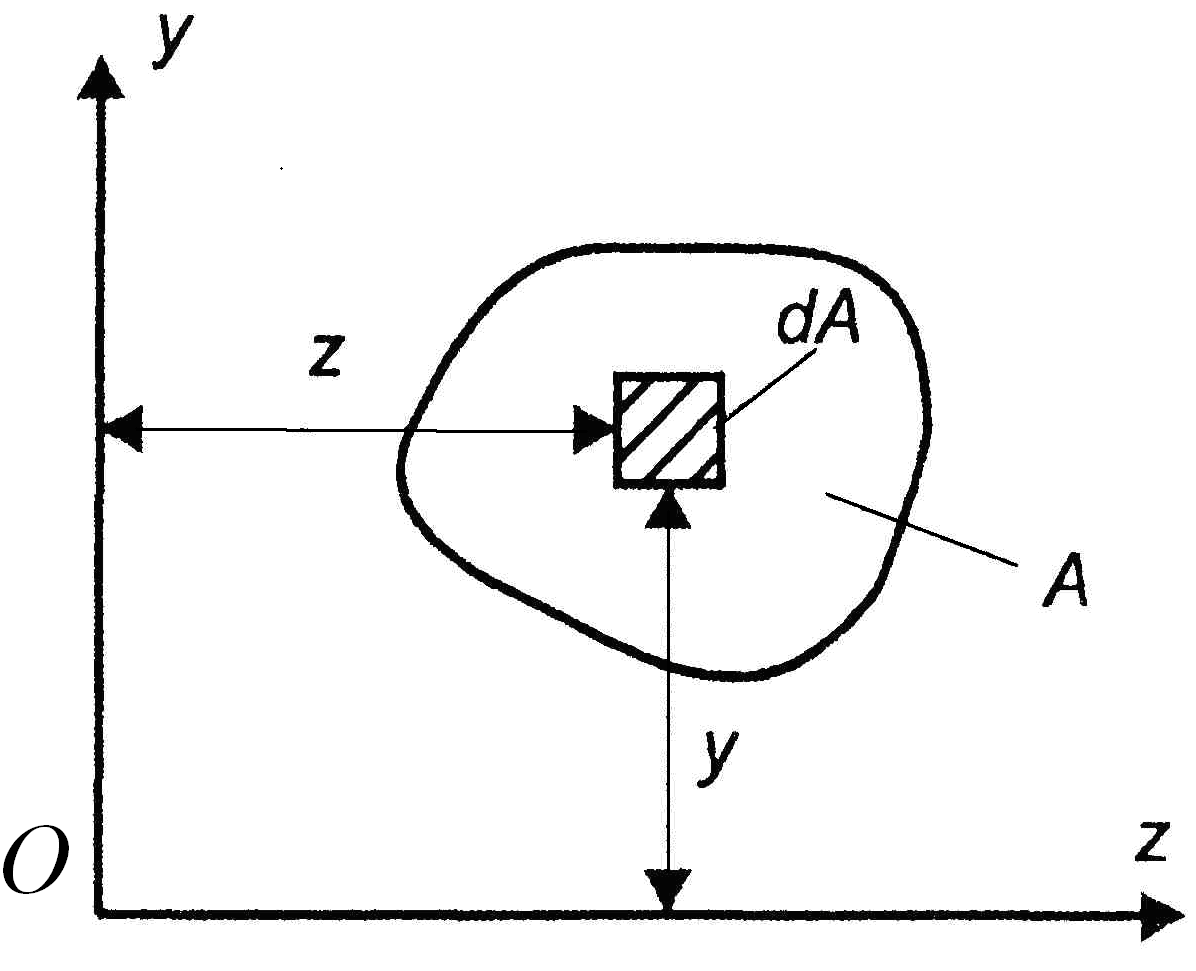
Рис.
3. Сечение произвольной формы в системе
координат z
О y
3.1.1. Свойства статических моментов площади сечения
Размерность статических моментов –
[длина3], обычно [м3] или
[см3].
Статические моменты могут быть
положительными, отрицательными или
равными нулю.
Ось, относительно которой статический
момент равен нулю, называется центральной.
Точка пересечения центральных осей
называется центром тяжести сечения.
Статический момент составного сечения
равен сумме статических моментов
элементов этого сечения. Это вытекает
из свойств определенного интеграла,
который можно вычислять по частям (в
нашем случае по частям площади А).
3.1.2. Определение положения центра тяжести
Рассмотрим
изменение статического момента при
параллельном переносе осей координат
(рис. 4). Расстояние между осями координат
обозначим а
и b.
Пусть известны статические моменты
относительно осей координат z,
y.
Найдем
статические моменты относительно
параллельных осей координат z1,
y1.

Рис.
4. Сечение произвольной формы в системах
координат с
параллельными
осями
По
определению: ![]() ,
,![]() .
.
Выделим
элементарную площадку dA
и запишем
связь между координатами площадки в
старой и новой системах координат: z1
= z
– b,
y1
= y
– a.
Тогда .
Аналогично
.
Найдем,
насколько надо сместить оси, чтобы они
стали центральными.
,
,
,
.
Здесь
ус
и zc
– координаты
центра тяжести.
При
их определении сечение разбиваем на
такие элементы, для которых эти координаты
известны (прямоугольник, круг, треугольник
и др.).
На
рис. 5 сечение разбито на три прямоугольника.
Статический момент каждого элемента
найдем формулам: Szi
= усi∙
Аi
и Syi
= zci
∙ Аi.

Рис.
5. Разбиение сложного сечения на простые
элементы
Суммарный
статический момент всего сечения, как
сказано выше, равен сумме статических
моментов элементов этого сечения:
Sz
= Sz1
+ Sz2
+ Sz3
= A1
∙ y1
+ A2
∙ y2
+ A3
∙ y3;
Sy
= Sy1
+ Sy2
+ Sy3
= A1
∙ z1
+ A2
∙ z2
+ A3
∙ z3,
а
площадь – сумме площадей элементов А
= A1
+ A2
+ A3.
Таким
образом, координаты центра тяжести
сечения можно представить в виде:
 ;
;
 .
.
где
Ai,
yi,
zi
– площади и координаты центра тяжести
элементов, на которые разбито сечение,
n
– количество
элементов.
Площадь стержня.
При расчетах элементов конструкций используются различные геометрические характеристики. Так, например, при растяжении и сжатии используется площадь поперечного сечения стержня. Она применяется при определении напряжений и деформаций растянутого или сжатого стержня, т.е. чем больше площадь поперечного сечения тем большую нагрузку сможет выдержать стержень.
Оказывается, при других деформациях эта геометрическая характеристика не является достаточной. Необходимо использовать другие, более сложные геометрические характеристики.
Статические моменты плоских сечений
Нетрудно убедиться, что в случае изгиба бруса площадь сечения не может служить характеристикой его жесткости. Действительно, из двух брусьев (рис. 2.2.1) с равновеликими площадями поперечных сечений первый при данной нагрузке деформируется значительно сильнее второго (например, при h/b = 2 прогибы первого бруса в четыре раза больше, чем второго).
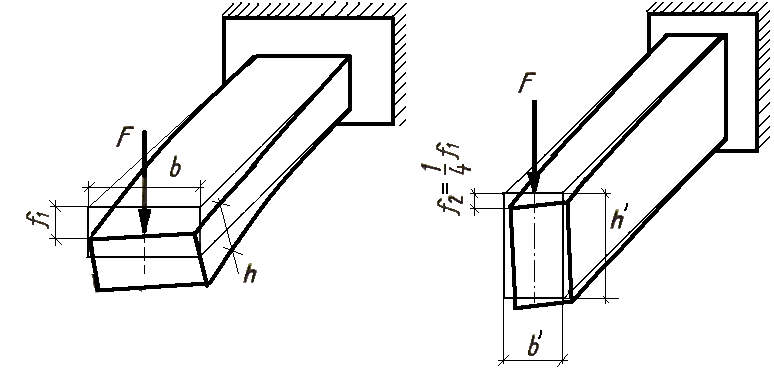
Рисунок 2.2.1
Следовательно, при одной и той же площади поперечного сечения стержня, но при разном расположении его стержень сопротивляется изгибу по разному. Это позволяет сделать вывод о том, что площадь поперечного сечения не может характеризовать сопротивляемость стержня изгибу и при изучении изгиба приходится вводить другие геометрические характеристики — статический момент площади (сечения).
Выполняя расчеты на прочность, необходимо бывает вычислять статические моменты всего сечения или части его относительно некоторых осей.
Рассмотрим произвольное поперечное сечение стержня в системе координат х,у, выдел элементарную площадку dА (рис. 2.2.2)
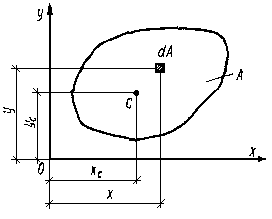
Рисунок 2.2.2
Статическим моментом сечения относительно данной оси называется сумма произведений элементарных площадей dА, на их расстояния до данной оси (например, х или у), которая распространяется на всю площадь сечения А.
Так, статические моменты сечения относительно осей х и у равны:
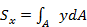 ;
; 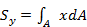 (2.2.1)
(2.2.1)
Статические моменты обычно выражаются в см3 или м3. При параллельном переносе осей значения статических моментов не остаются постоянными, а изменяются и могут иметь как положительное, так и отрицательное значение. Следовательно, среди семейства параллельных осей существует единственная ось, относительно которой статический момент равен нулю
Ось, относительно которой статический момент равен нулю, называется центральной.
Точка пересечения центральных осей называется центром тяжести сечения.
Можно показать, что и относительно любой оси, проходящей через центр тяжести сечения, статический момент равен нулю. Для изображенного на рис. 2.2.2 сечения центр тяжести располагается в точке С, его координатами являются ординаты хс и ус. Все оси, которые проходят через эту точку, будут центральными и относительно таких осей статический момент равен нулю.
На основании теоремы Вариньона следует, что
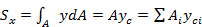 ;
; 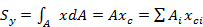 (2.2.2)
(2.2.2)
Следовательно, статический момент площади А относительно какой-либо оси равен произведению всей площади на расстояние от ее центра тяжести до этой оси.
Из выражений (2.2.2) получим формулы для определения координат центра тяжести сечения:
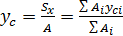 ;
; 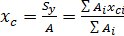 (2.2.3)
(2.2.3)
Заметим, что последняя форма записи в выражениях (2.2.3) относится к определению координат центра тяжести сложного сечения разбитого на простейшие составные части, для которых известны площади А и положение центра тяжести и ус
Для большинства сечений определение положения центра тяжести упрощается. Так, если сечения имеют ось или центр симметрии, то центр тяжести в таких сечениях находится соответственно на оси симметрии или в центре симметрии.
