Какими свойствами обладает произведение матриц

Умноже́ние ма́триц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется произведе́нием ма́триц. Элементы новой матрицы получаются из элементов старых матриц в соответствии с правилами, проиллюстрированными ниже.

Матрицы и могут быть перемножены, если они совместимы в том смысле, что число столбцов матрицы равно числу строк .

Матрицы обладают многими алгебраическими свойствами умножения, присущими обычным числам, за исключением коммутативности.

Для квадратных матриц, помимо умножения, может быть введена операция возведения матрицы в степень и обратная матрица.

Тогда как матрицы используются для описания, в частности, преобразований математических пространств (поворот, отражение, растяжение и другие), произведение матриц будет описывать композицию преобразований.

Определение[править | править код]

Пусть даны две прямоугольные матрицы и размерности и соответственно:

Тогда матрица размерностью :

в которой:

называется их произведением.

Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что матрицы согласованы. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка.

Таким образом, из существования произведения вовсе не следует существование произведения

Иллюстрация[править | править код]

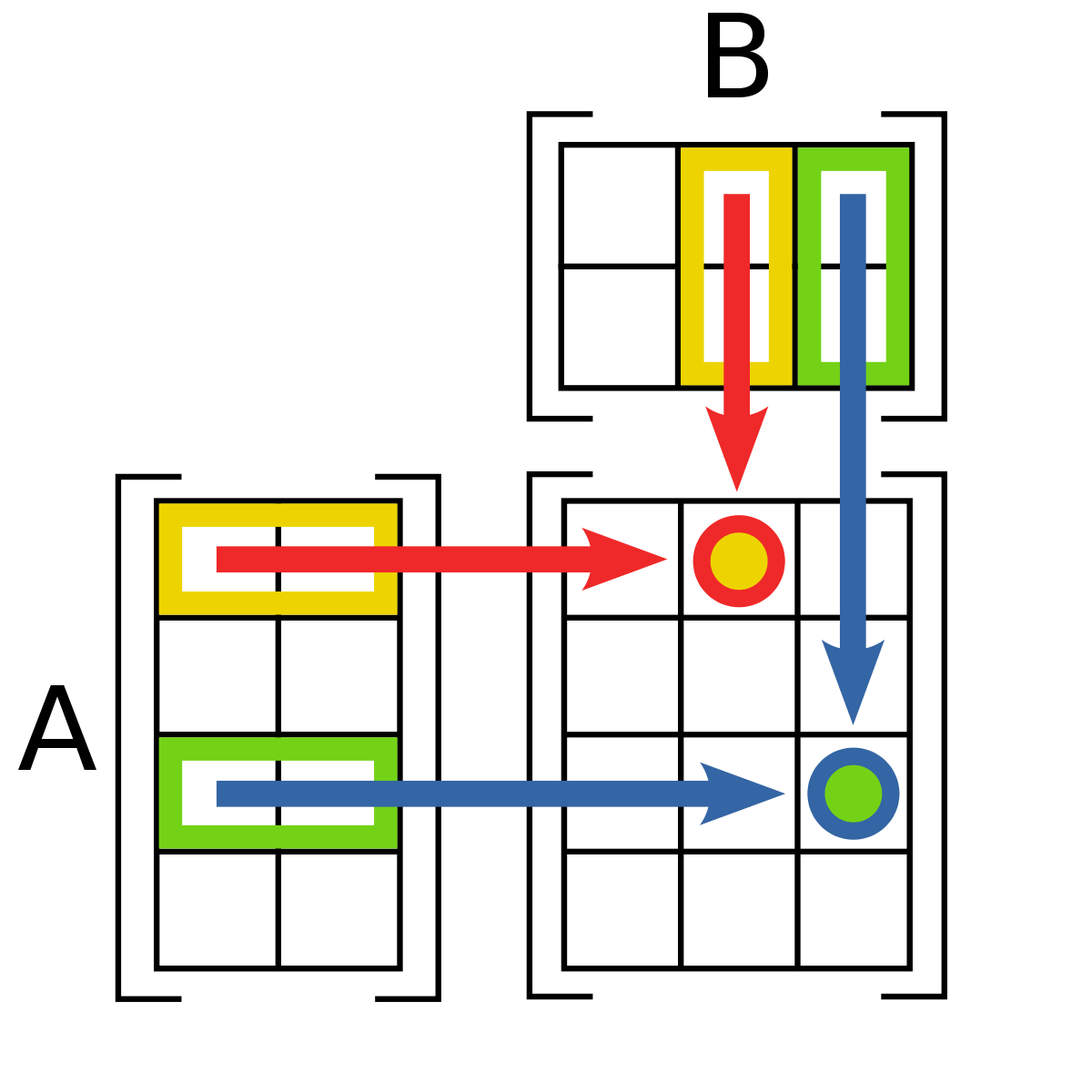
Произведение матриц AB состоит из всех возможных комбинаций скалярных произведений вектор-строк матрицы A и вектор-столбцов матрицы B. Элемент матрицы AB с индексами i, j есть скалярное произведение i-ой вектор-строки матрицы A и j-го вектор-столбца матрицы B.

Иллюстрация справа демонстрирует вычисление произведения двух матриц A и B, она показывает как каждые пересечения в произведении матриц соответствуют строкам матрицы A и столбцам матрицы B. Размер результирующей матрицы всегда максимально возможный, то есть для каждой строки матрицы A и столбца матрицы B есть всегда соответствующее пересечение в произведении матрицы.

Значения на пересечениях, отмеченных кружочками, будут:

В общем случае, произведение матриц не является коммутативной операцией. К примеру:

Элемент произведения матриц, приведённых выше, вычисляется следующим образом

Первая координата в обозначении матрицы обозначает строку, вторая координата — столбец; этот порядок используют как при индексации, так и при обозначении размера. Элемент на пересечении строки и столбца результирующей матрицы является скалярным произведением -й строки первой матрицы и -го столбца второй матрицы.
Это объясняет почему ширина и высота умножаемых матриц должны совпадать: в противном случае скалярное произведение не определено.

Обсуждение[править | править код]

Увидеть причины описанного правила матричного умножения легче всего, рассмотрев умножение вектора на матрицу.

Последнее естественно вводится исходя из того, что при разложении векторов по базису действие (любого) линейного оператора A даёт выражение компонент вектора v’ = Av:

То есть линейный оператор оказывается представлен матрицей, векторы — векторами-столбцами, а действие оператора на вектор — матричным умножением вектора-столбца слева на матрицу оператора (это частный случай матричного умножения, когда одна из матриц — вектор-столбец — имеет размер ).

(Равно переход к любому новому базису при смене координат представляется полностью аналогичным выражением, только в этом случае уже не компоненты нового вектора в старом базисе, а компоненты старого вектора в новом базисе; при этом  — элементы матрицы перехода к новому базису).

Рассмотрев последовательное действие на вектор двух операторов: сначала A, а потом B (или преобразование базиса A, а затем преобразование базиса B), дважды применив нашу формулу, получим:

откуда видно, что композиции BA действия линейных операторов A и B (или аналогичной композиции преобразований базиса) соответствует матрица, вычисляемая по правилу произведения соответствующих матриц:

Определённое таким образом произведение матриц оказывается совершенно естественным и очевидно полезным (даёт простой и универсальный способ вычисления композиций произвольного количества линейных преобразований).

Свойства[править | править код]

Сочетательное свойство, ассоциативность:

Распределительное свойство, дистрибутивность относительно сложения:

.

Произведение матрицы на единичную матрицу подходящего порядка равно самой матрице:

Произведение матрицы на нулевую матрицу подходящей размерности равно нулевой матрице:

Если и  — квадратные матрицы одного и того же порядка, то произведение матриц обладает ещё рядом свойств.

Умножение матриц в общем случае некоммутативно:

Если , то матрицы и называются коммутирующими между собой.

Простейшие примеры коммутирующих матриц:

Определитель и след произведения не зависят от порядка умножения матриц:

Обратная матрица[править | править код]

Квадратная матрица называется неособенной (невырожденной), если она имеет единственную обратную матрицу такую, что выполняется условие:

В противном случае матрица называется особенной (вырожденной).

Матрица порядка является невырожденной в том и только в том случае, если в этом случае есть квадратная матрица того же порядка

где  — алгебраическое дополнение элемента в определителе

Алгоритмы быстрого перемножения матриц[править | править код]

Сложность вычисления произведения матриц по определению составляет , однако существуют более эффективные алгоритмы[1], применяющиеся для больших матриц. Вопрос о предельной скорости умножения больших матриц, также как и вопрос о построении наиболее быстрых и устойчивых практических алгоритмов умножения больших матриц остаётся одной из нерешённых проблем линейной алгебры.

• Алгоритм Штрассена (1969)

Первый алгоритм быстрого умножения больших матриц был разработан Фолькером Штрассеном[2] в 1969. В основе алгоритма лежит рекурсивное разбиение матриц на блоки 2Х2. Штрассен доказал, что матрицы 2Х2 можно некоммутативно перемножить с помощью семи умножений, поэтому на каждом этапе рекурсии выполняется семь умножений вместо восьми. В результате асимптотическая сложность этого алгоритма составляет . Недостатком данного метода является бо́льшая сложность программирования по сравнению со стандартным алгоритмом, слабая численная устойчивость и больший объём используемой памяти. Разработан ряд алгоритмов на основе метода Штрассена, которые улучшают численную устойчивость, скорость по константе и другие его характеристики. Тем не менее, в силу простоты алгоритм Штрассена остаётся одним из практических алгоритмов умножения больших матриц. Штрассен также выдвинул следующую гипотезу Штрассена: для сколь угодно малого существует алгоритм, при достаточно больших натуральных n гарантирующий перемножение двух матриц размера за операций.

• Дальнейшие улучшения показателя степени ω для скорости матричного умножения

В дальнейшем оценки скорости умножения больших матриц многократно улучшались. Однако эти алгоритмы носили теоретический, в основном приближённый характер. В силу неустойчивости алгоритмов приближённого умножения в настоящее время они не используются на практике.

• Алгоритм Пана (1978)

В 1978 Пан[3] предложил свой метод умножения матриц, сложность которого составила Θ(n2.78041).

• Алгоритм Бини (1979)

В 1979 группа итальянских учёных во главе с Бини[4] разработала алгоритм умножения матриц с использованием тензоров. Его сложность составляет Θ(n2.7799).

• Алгоритмы Шёнхаге (1981)

В 1981 Шёнхаге[5] представил метод, работающий со скоростью Θ(n2.695). Оценка получена с помощью подхода, названного частичным матричным умножением. Позже ему удалось получить оценку Θ(n2.6087).
Затем Шёнхаге на базе метода прямых сумм получил оценку сложности Θ(n2.548). Романи сумел понизить оценку до Θ(n2.5166), а Пан — до Θ(n2.5161).

• Алгоритм Копперсмита — Винограда (1990)

В 1990 Копперсмит и Виноград[6] опубликовали алгоритм, который в модификации Вильямс Василевской[7]2011 года умножает матрицы со скоростью O(n2.3727). Этот алгоритм использует идеи, схожие с алгоритмом Штрассена. На сегодняшний день модификации алгоритма Копперсмита-Винограда являются наиболее асимптотически быстрыми. Но тот факт, что полученные улучшения ничтожны, позволяет говорить о существовании «барьера Копперсмита-Винограда» в асимптотических оценках скорости алгоритмов. Алгоритм Копперсмита-Винограда эффективен только на матрицах астрономического размера и на практике применяться не может.

• Связь с теорией групп (2003)

В 2003 Кох и др. рассмотрели в своих работах[8] алгоритмы Штрассена и Копперсмита-Винограда в контексте теории групп. Они показали, что гипотеза Штрассена справедлива, если выполняется одна из гипотез теории групп[9].

Степени матриц[править | править код]

Квадратные матрицы можно многократно умножать сами на себя так же, как обычные числа, так как у них одинаковое число строк и столбцов.
Такое последовательное умножение можно назвать возведением матрицы в степень — это будет частный случай обычного умножения нескольких матриц. У прямоугольных матриц число строк и столбцов разное, поэтому их никогда нельзя возводить в степень.
Матрица A размерности n × n, возведённая в степень, определяется формулой

и обладает следующими свойствами (λ — некоторый скаляр):

Нулевая степень:

где E — единичная матрица. Это аналог того факта, что нулевая степень любого числа равна единице.

Умножение на скаляр:

Определитель:

Наивный способ вычисления степени матрицы — это умножать k раз матрицу A на результат предыдущего умножения, начиная с единичной матрицы, как это часто делают для скаляров.
Для диагонализируемых матриц существует лучший метод, основанный на использовании спектрального разложения матрицы A.
Ещё один метод, основанный на теореме Гамильтона — Кэли, строит более эффективное выражение для Ak, в котором в требуемую степень возводится скаляр, а не вся матрица.

Особый случай составляют диагональные матрицы.
Так как произведение диагональных матриц сводится к умножению соответствующих диагональных элементов, то k-ая степень диагональной матрицы A состоит из элементов, возведённых в требуемую степень:

Таким образом, возвести диагональную матрицу в степень несложно.
При возведении произвольной матрицы (не обязательно диагональной) в степень часто полезным оказывается использовать сначала свойства диагонализируемых матриц.

Используя умножение матриц и возведение матриц в степень, можно определить другие операции над матрицами. Например, матричная экспонента может быть определена через степенной ряд, матричный логарифм[en] — как обратная к матричной экспоненте функция и так далее.

См. также[править | править код]

• Произведение Кронекера

Литература[править | править код]

• Корн Г., Корн Т. Алгебра матриц и матричное исчисление // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 392—394.

Примечания[править | править код]