Какими свойствами обладает правильная пирамида
Пирами́да (от др.-греч. πυραμίς, род. п. πυραμίδος) — многогранник, одна из граней которого (называемая основанием) — произвольный многоугольник, а остальные грани (называемые боковыми гранями) — треугольники, имеющие общую вершину[1]. По числу углов основания различают пирамиды треугольные (тетраэдр), четырёхугольные и т. д.
Пирамида является частным случаем конуса[2].
История развития пирамиды в геометрии[править | править код]
Начало геометрии пирамиды было положено в Древнем Египте и Вавилоне, однако активное развитие получило в Древней Греции. Объем пирамиды был известен древним египтянам. Первым греческим математиком, кто установил, чему равен объём пирамиды, был Демокрит
[3], а доказал Евдокс Книдский. Древнегреческий математик Евклид систематизировал знания о пирамиде в XII томе своих «Начал», а также вывел первое определение пирамиды: телесная фигура, ограниченная плоскостями, которые от одной плоскости сходятся в одной точке (книга XI, определение 12[4]).
Элементы пирамиды[править | править код]
SO — высота
SF — апофема
OF — радиус вписанной в основание окружности
- апофема — высота боковой грани правильной пирамиды, проведённая из её вершины;
- боковые грани — треугольники, сходящиеся в вершине;
- боковые ребра — общие стороны боковых граней;
- вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания;
- высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра);
- диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания;
- основание — многоугольник, которому не принадлежит вершина пирамиды.
Развёртка пирамиды[править | править код]
Развёртка правильной пятиугольной пирамиды:
1. в плоскости основания («звезда»)
2. в плоскости одной из боковых граней
Развёрткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга).
Приступая к изучению развёртки поверхности, последнюю целесообразно рассматривать как гибкую, нерастяжимую плёнку. Некоторые из представленных таким образом поверхностей можно путём изгибания совместить с плоскостью. При этом, если отсек поверхности может быть совмещён с плоскостью без разрывов и склеивания, то такую поверхность называют развёртывающейся, а полученную плоскую фигуру — её развёрткой.
Свойства[править | править код]
Если все боковые рёбра равны, то:
- вокруг основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр;
- боковые рёбра образуют с плоскостью основания равные углы;
- также верно и обратное, то есть если боковые рёбра образуют с плоскостью основания равные углы, или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые рёбра пирамиды равны.
Если боковые грани наклонены к плоскости основания под одним углом, то:
- в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр;
- высоты боковых граней равны;
- площадь боковой поверхности равна половине произведения периметра основания на высоту боковой грани.
Теоремы, связывающие пирамиду с другими геометрическими телами[править | править код]
Описание сферы вокруг правильной пирамиды:
SD — высота пирамиды.
AD — радиус окружности, описывающей основание.
В — середина ребра боковой грани
С — точка пересечения плоскостей проходящих через середину рёбер перпендикулярно им.
AC=CS — радиус сферы описывающей пирамиду
Сфера, вписанная в правильную пирамиду:
D — центр основания
SF — апофема
ASD — биссекторная плоскость угла между боковыми гранями
BCE — биссекторная плоскость угла между основанием и боковой гранью
С — точка пересечения всех биссекторных плоскостей
CK=CD — радиус сферы вписанной в пирамиду
Сфера[править | править код]
- около пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многоугольник, вокруг которого можно описать окружность (необходимое и достаточное условие)[5]. Центром сферы будет точка пересечения плоскостей, проходящих через середины рёбер пирамиды перпендикулярно им. Из этой теоремы следует, что как около любой треугольной, так и около любой правильной пирамиды можно описать сферу;
- в пирамиду можно вписать сферу тогда, когда биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.
Конус[править | править код]
- Конус называется вписанным в пирамиду, если вершины их совпадают, а его основание вписано в основание пирамиды. Причём вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны между собой (необходимое и достаточное условие);[6]
- Конус называется описанным около пирамиды, когда их вершины совпадают, а его основание описано около основания пирамиды. Причём описать конус около пирамиды можно только тогда, когда все боковые рёбра пирамиды равны между собой (необходимое и достаточное условие);
- Высоты у таких конусов и пирамид равны между собой.
Цилиндр[править | править код]
- Цилиндр называется вписанным в пирамиду, если одно его основание совпадает с окружностью вписанной в сечение пирамиды плоскостью, параллельной основанию, а другое основание принадлежит основанию пирамиды.
- Цилиндр называется описанным около пирамиды, если вершина пирамиды принадлежит его одному основанию, а другое его основание описано около основания пирамиды. Причём описать цилиндр около пирамиды можно только тогда, когда в основании пирамиды — вписанный многоугольник (необходимое и достаточное условие).
Формулы, связанные с пирамидой[править | править код]
- Объём пирамиды может быть вычислен по формуле:
где — площадь основания и — высота;[7]
где — объём параллелепипеда;
- Также объём треугольной пирамиды (тетраэдра) может быть вычислен по формуле[8]:
где — скрещивающиеся рёбра , — расстояние между и , — угол между и ;
- Боковая поверхность — это сумма площадей боковых граней:
- Полная поверхность — это сумма площади боковой поверхности и площади основания:
- Для нахождения площади боковой поверхности в правильной пирамиде можно использовать формулы:
где — апофема , — периметр основания, — число сторон основания, — боковое ребро, — плоский угол при вершине пирамиды.
Особые случаи пирамиды[править | править код]
Правильная пирамида[править | править код]
Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания.
Тогда она обладает такими свойствами:
Прямоугольная пирамида[править | править код]
Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.
Тетраэдр[править | править код]
Тетраэдром называется треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды. Кроме того, существует большое различие между понятиями «правильная треугольная пирамида» и «правильный тетраэдр». Правильная треугольная пирамида — это пирамида с правильным треугольником в основании (грани же должны быть равнобедренными треугольниками). Правильным тетраэдром является тетраэдр, у которого все грани являются равносторонними треугольниками.
См. также[править | править код]
- Усечённая пирамида
- Бипирамида
Примечания[править | править код]
- ↑ Александров А. Д., Вернер А. Л. Геометрия. Учебник для 10—11 классов общеобразовательных учреждений. — 2-е изд. — М.: Просвещение, 2003. — 271 с. — ISBN 5-09-010773-4.
- ↑ Математика в понятиях, определениях и терминах. Ч. 1. Пособие для учителей. Под ред. Л. В. Сабинина. М., Просвещение, 1978. 320 с. С. 253.
- ↑ Б. Л. ван дер Варден. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. — 3-е изд.. — М.: КомКнига, 2007. — 456 с. — ISBN 978-5-484-00848-3.
- ↑ М. Е. Ващенко-Захарченко. Начала Евклида с пояснительным введением и толкованиями. — Киев, 1880. — С. 473. — 749 с.
- ↑ Саакян С. М., Бутузов В. Ф. Изучение геометрии в 10—11-х классах: книга для учителя. — 4-е изд., дораб.. — М.: Просвещение, 2010. — 248 с. — (Математика и информатика). — ISBN 978-5-09-016554-9.
- ↑ Погорелов А. В. Геометрия: Учебник для 10—11 классов общеобразовательных учреждений. — 8-е изд. — М.: Просвещение, 2008. — 175 с. — 60 000 экз. — ISBN 978-5-09-019708-3.
- ↑ Геометрия по Киселёву, §357.
- ↑ Кушнир И. А. Триумф школьной геометрии. — К.: Наш час, 2005. — 432 с. — ISBN 966-8174-01-1.
- ↑ Готман Э. Свойства правильной пирамиды, вписанной в сферу Архивная копия от 22 января 2012 на Wayback Machine // Квант. — 1998. — № 4.
Литература[править | править код]
- Александров А. Д., Вернер А. Л. Геометрия. Учебник для 10—11 классов общеобразовательных учреждений. — 2-е изд. — М.: Просвещение, 2003. — 271 с. — ISBN 5-09-010773-4.
- Калинин А. Ю., Терешин Д. А. Стереометрия. 11 класс. — 2-е изд. — М.: Физматкнига, 2005. — 332 с. — ISBN 5-89155-134-9.
- Погорелов А. В. Геометрия: Учебник для 10—11 классов общеобразовательных учреждений. — 8-е изд. — М.: Просвещение, 2008. — 175 с. — 60 000 экз. — ISBN 978-5-09-019708-3.
Ссылки[править | править код]
- Бумажные модели пирамид (англ.)
- «Начала» Евклида.
Определение.
Пирамида — это многогранная объемная фигура, ограниченная плоским многоугольником (основой) и треугольниками, имеющих общую вершину, не лежащую в плоскости основания.
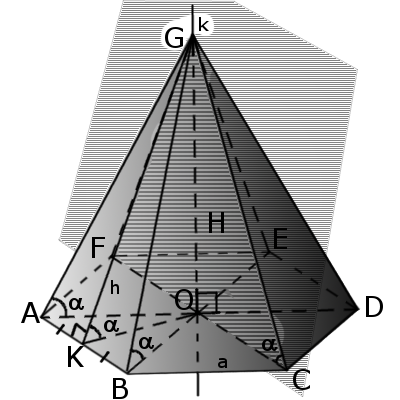 |
| Рис.1 |
Определение. Боковая грань — это треугольник, у которого один угол лежит в вершине пирамиды, а противоположная ему сторона совпадает со стороной основания (многоугольника).
Определение. Боковые ребра — это общие стороны боковых граней. У пирамиды столько ребер сколько углов у многоугольника.
Определение. Высота пирамиды — это перпендикуляр, опущенный из вершины на основание пирамиды.
Определение. Апофема — это перпендикуляр боковой грани пирамиды, опущенный из вершины пирамиды к стороне основания.
Определение. Диагональное сечение — это сечение пирамиды плоскостью, проходящей через вершину пирамиды и диагональ основания.
Определение. Правильная пирамида — это пирамида, в которой основой является правильный многоугольник, а высота опускается в центр основания.
Объём и площадь поверхности пирамиды
Формула. Объём пирамиды через площадь основы и высоту:
Определение. Боковая поверхность пирамиды — это совокупная площадь всех боковых граней пирамиды.
Определение. Полная поверхность пирамиды — это совокупность площадей боковой поверхности и площади основания пирамиды.
Формула. Площадь боковой поверхности правильной пирамиды через периметр основания и апофему:
Свойства пирамиды
Если все боковые ребра равны, то вокруг основания пирамиды можно описать окружность, а центр основания совпадает с центром окружности. Также перпендикуляр, опущенный из вершины, проходит через центр основания (круга).
Если все боковые ребра равны, то они наклонены к плоскости основания под одинаковыми углами.
Боковые ребра равны тогда, когда они образуют с плоскостью основания равные углы или если вокруг основания пирамиды можно описать окружность.
Если боковые грани наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проектируется в ее центр.
Если боковые грани наклонены к плоскости основания под одним углом, то апофемы боковых граней равны.
Свойства правильной пирамиды
1. Вершина пирамиды равноудалена от всех углов основания.
2. Все боковые ребра равны.
3. Все боковые ребра наклонены под одинаковыми углами к основанию.
4. Апофемы всех боковых граней равны.
5. Площади всех боковых граней равны.
6. Все грани имеют одинаковые двугранные (плоские) углы.
7. Вокруг пирамиды можно описать сферу. Центром описанной сферы будет точка пересечения перпендикуляров, которые проходят через середину ребер.
8. В пирамиду можно вписать сферу. Центром вписанной сферы будет точка пересечения биссектрис, исходящие из угла между ребром и основанием.
9. Если центр вписанной сферы совпадает с центром описанной сферы, то сумма плоских углов при вершине равна π или наоборот, один угол равен π/n, где n — это количество углов в основании пирамиды.
Связь пирамиды со сферой
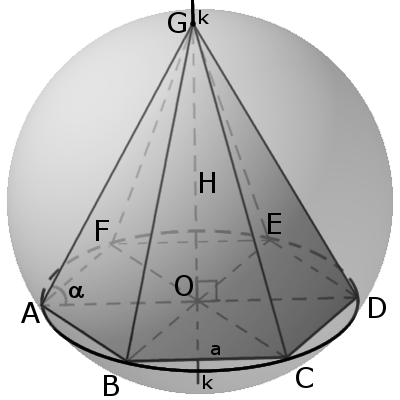
Вокруг пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многогранник вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы будет точка пересечения плоскостей, проходящих перпендикулярно через середины боковых ребер пирамиды.
Вокруг любой треугольной или правильной пирамиды всегда можно описать сферу.
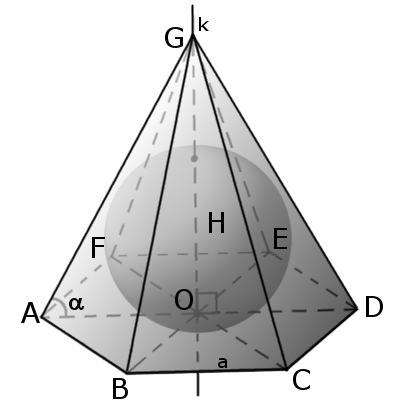
В пирамиду можно вписать сферу, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.
Связь пирамиды с конусом
Конус называется вписанным в пирамиду, если их вершины совпадают, а основание конуса вписано в основание пирамиды.
Конус можно вписать в пирамиду, если апофемы пирамиды равны между собой.
Конус называется описанным вокруг пирамиды, если их вершины совпадают, а основание конуса описана вокруг основания пирамиды.
Конус можно описать вокруг пирамиды если, все боковые ребра пирамиды равны между собой.
Связь пирамиды с цилиндром
Пирамида называется вписанной в цилиндр, если вершина пирамиды лежит на одной основе цилиндра, а основание пирамиды вписано в другую основу цилиндра.
Цилиндр можно описать вокруг пирамиды если вокруг основания пирамиды можно описать окружность.
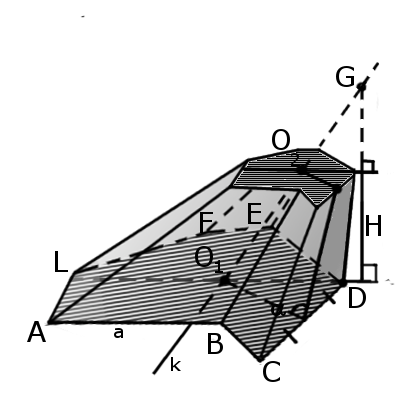
Определение. Усеченная пирамида (пирамидальная призма) — это многогранник, который находится между основанием пирамиды и плоскостью сечения, параллельной основанию. Таким образом пирамида имеет большую основу и меньшую основу, которая подобна большей. Боковые грани представляют собой трапеции.
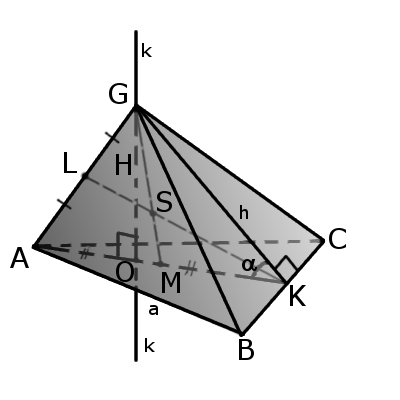
Определение. Треугольная пирамида (четырехгранник) — это пирамида в которой три грани и основание являются произвольными треугольниками.
В четырехгранник четыре грани и четыре вершины и шесть ребер, где любые два ребра не имеют общих вершин но не соприкасаются.
Каждая вершина состоит из трех граней и ребер, которые образуют трехгранный угол.
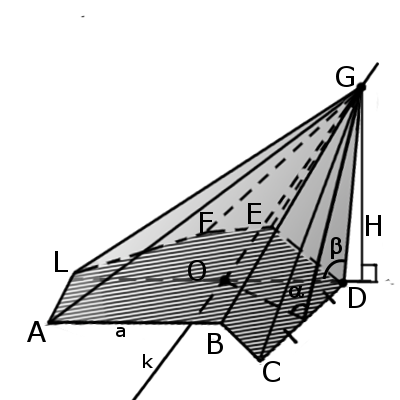
Отрезок, соединяющий вершину четырехгранника с центром противоположной грани называется медианой четырехгранника (GM).
Бимедианой называется отрезок, соединяющий середины противоположных ребер, которые не соприкасаются (KL).
Все бимедианы и медианы четырехгранника пересекаются в одной точке (S). При этом бимедианы делятся пополам, а медианы в отношении 3:1 начиная с вершины.

Определение. Наклонная пирамида — это пирамида в которой одно из ребер образует тупой угол (β) с основанием.
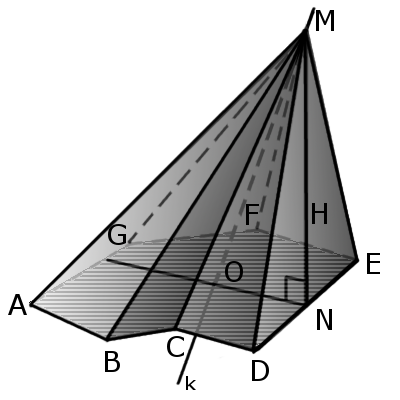
Определение. Прямоугольная пирамида — это пирамида в которой одна из боковых граней перпендикулярна к основанию.
Определение. Остроугольная пирамида — это пирамида в которой апофема больше половины длины стороны основания.
Определение. Тупоугольная пирамида — это пирамида в которой апофема меньше половины длины стороны основания.
Определение. Правильный тетраэдр — четырехгранник у которого все четыре грани — равносторонние треугольники. Он является одним из пяти правильных многоугольников. В правильного тетраэдра все двугранные углы (между гранями) и трехгранные углы (при вершине) равны.
Определение. Прямоугольный тетраэдр называется четырехгранник у которого прямой угол между тремя ребрами при вершине (ребра перпендикулярны). Три грани образуют прямоугольный трехгранный угол и грани являются прямоугольными треугольниками, а основа произвольным треугольником. Апофема любой грани равна половине стороны основы, на которую падает апофема.
Определение. Равногранный тетраэдр называется четырехгранник у которого боковые грани равны между собой, а основание — правильный треугольник. У такого тетраэдра грани это равнобедренные треугольники.
Определение. Ортоцентричный тетраэдр называется четырехгранник у которого все высоты (перпендикуляры), что опущены с вершины до противоположной грани, пересекаются в одной точке.
Определение. Звездная пирамида называется многогранник у которого основой является звезда.
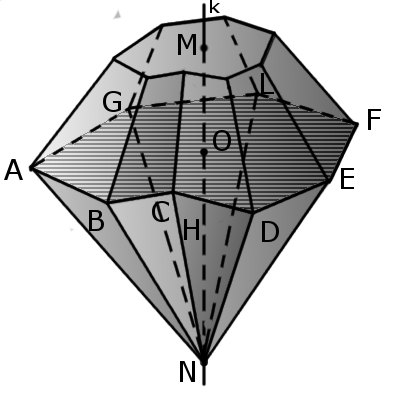
Определение. Бипирамида — многогранник, состоящий из двух различных пирамид (также могут быть срезаны пирамиды), имеющих общую основу, а вершины лежат по разные стороны от плоскости основания.
Пирамида Пирамида — (от греч. pyramis, род. п. pyramidos), многогранник, Общая вершина боковых граней называется вершиной пирамиды. Высотой
Элементы пирамиды |


