Какими свойствами обладает показательная функция

Формулы с показательной функцией

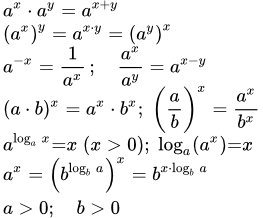
Приведены справочные данные по показательной функции – основные свойства, графики и формулы. Рассмотрены следующие вопросы: область определения, множество значений, монотонность, обратная функция, производная, интеграл, разложение в степенной ряд и представление посредством комплексных чисел.

Содержание

ОпределениеСвойства показательной функцииЧастные значенияГрафики показательной функцииВозрастание, убываниеОбратная функцияДифференцирование показательной функцииПроизводная показательной функцииПример дифференцирования показательной функцииИнтегралВыражения через комплексные числаРазложение в рядСм. также: Экспонента, е в степени х
Логарифм — свойства, формулы, график
Степенная функция и корни

Определение

Показательная функция – это обобщение произведения n чисел, равных a:
y(n) = an = a·a·a···a,
на множество действительных чисел x:
y(x) = ax.
Здесь a – фиксированное действительное число, которое называют основанием показательной функции.
Показательную функцию с основанием a также называют экспонентой по основанию a.

Обобщение выполняется следующим образом.
При натуральном x = 1, 2, 3,…, показательная функция является произведением x множителей:
.
При этом она обладает свойствами (1.5-8) (см. ниже ⇓), которые следуют из правил умножения чисел. При нулевом и отрицательных значениях целых чисел , показательную функцию определяют по формулам (1.9-10). При дробных значениях x = m/n рациональных чисел, , ее определяют по формуле(1.11). Для действительных , показательную функцию определяют как предел последовательности:
,
где – произвольная последовательность рациональных чисел, сходящаяся к x: .
При таком определении, показательная функция определена для всех , и удовлетворяет свойствам (1.5-8), как и для натуральных x.

Строгая математическая формулировка определения показательной функции и доказательство ее свойств приводится на странице «Определение и доказательство свойств показательной функции».

Свойства показательной функции

Показательная функция y = ax, имеет следующие свойства на множестве действительных чисел ():
(1.1) определена и непрерывна, при , для всех ;
(1.2) при a ≠ 1 имеет множество значений ;
(1.3) строго возрастает при , строго убывает при ,
является постоянной при ;
(1.4) при ;
при ;
(1.5) ;
(1.6) ;
(1.7) ;
(1.8) ;
(1.9) ;
(1.10) ;
(1.11) , .

Другие полезные формулы.
.
Формула преобразования к показательной функции с другим основанием степени:

При b = e, получаем выражение показательной функции через экспоненту:

Частные значения

, , , , .

Графики показательной функции

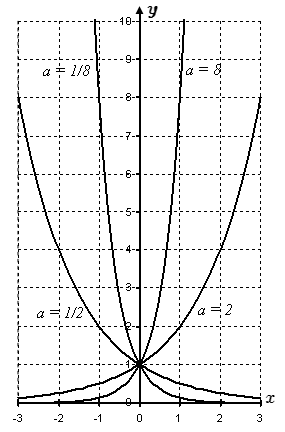
Графики показательной функции y = ax при различных значениях основания a.

На рисунке представлены графики показательной функции
y(x) = a x
для четырех значений основания степени: a = 2, a = 8, a = 1/2 и a = 1/8. Видно, что при a > 1 показательная функция монотонно возрастает. Чем больше основание степени a, тем более сильный рост. При 0 < a < 1 показательная функция монотонно убывает. Чем меньше показатель степени a, тем сильнее убывание.

Возрастание, убывание

Показательная функция, при является строго монотонной, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице.

	y = ax, a > 1	y = ax, 0 < a < 1
Область определения	– ∞ < x < + ∞	– ∞ < x < + ∞
Область значений	0 < y < + ∞	0 < y < + ∞
Монотонность	монотонно возрастает	монотонно убывает
Нули, y = 0	нет	нет
Точки пересечения с осью ординат, x = 0	y = 1	y = 1
+ ∞	0
0	+ ∞

Обратная функция

Обратной для показательной функции с основанием степени a является логарифм по основанию a.

Если , то
.
Если , то
.

Дифференцирование показательной функции

Для дифференцирования показательной функции, ее основание нужно привести к числу e, применить таблицу производных и правило дифференцирования сложной функции.

Для этого нужно использовать свойство логарифмов
и формулу из таблицы производных:
.

Пусть задана показательная функция:
.
Приводим ее к основанию e:

Применим правило дифференцирования сложной функции. Для этого вводим переменную

Тогда

Из таблице производных имеем (заменим переменную x на z):
.
Поскольку – это постоянная, то производная z по x равна
.
По правилу дифференцирования сложной функции:
.

Производная показательной функции

.
Производная n-го порядка:
.
Вывод формул > > >

Пример дифференцирования показательной функции

Найти производную функции
y = 35x

Решение

Выразим основание показательной функции через число e.
3 = e ln 3
Тогда
.
Вводим переменную
.
Тогда

Из таблицы производных находим:
.
Поскольку 5ln 3 – это постоянная, то производная z по x равна:
.
По правилу дифференцирования сложной функции имеем:
.

Ответ

Интеграл

Выражения через комплексные числа

Рассмотрим функцию комплексного числа z:
f(z) = a z
где z = x + iy; i2 = – 1.
Выразим комплексную постоянную a через модуль r и аргумент φ:
a = r e i φ
Тогда

.
Аргумент φ определен не однозначно. В общем виде
φ = φ0 + 2πn,
где n – целое. Поэтому функция f(z) также не однозначна. Часто рассматривают ее главное значение
.

Разложение в ряд

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Автор: Олег Одинцов. Опубликовано: 21-02-2014 Изменено: 19-11-2018

См. также: Экспонента, е в степени х
Логарифм — свойства, формулы, график
Степенная функция и корни

Источник

Определение и свойства

Определение
Показательная функция f(n) = an, с основанием a, от натурального аргумента n – это произведение n множителей, каждый из которых равен a:
.
Здесь .

При она обладает следующими свойствами, вытекающих из правил умножения чисел:
(1.1) a x> 0 при a > 0;
(1.2) строго возрастает при a > 1 и строго убывает при 0 < a < 1;
(1.3) ;
(1.4) ;
(1.5) .

Если положить:
(1.6) ,
(1.7) ,
то показательная функция становится определенной и для целых чисел. При этом свойства (1.1-5) по прежнему выполняются, в которых , . Подробнее ⇓

Если положить:
(1.8) ,
где , то показательная функция становится определенной и для рациональных чисел . При этом выполняются свойства (1.1-7). В них , . Подробнее ⇓

Далее, основываясь на свойствах показательной функции (1.1-8), определенной на множестве рациональных чисел, мы определяем эту функцию на множестве действительных чисел и даем доказательство ее свойств.

Лемма
Пусть последовательность рациональных чисел сходится к действительному числу x:
.
И пусть a > 0. Тогда существует предел последовательности :
,
и этот предел может зависеть от числа x, но не зависит от последовательности .
Доказательство ⇓

Определение показательной функции
Показательная функция f(x) = ax, с основанием a > 0 – это предел последовательности
,
где есть произвольная последовательность рациональных чисел, стремящаяся к x:
.

Это определение справедливо и в случае, если x является рациональным числом. При этом совпадает со значением показательной функции, определяемом на множестве рациональных чисел. Чтобы убедиться в этом, достаточно в качестве последовательности взять последовательность с постоянными членами .

Заметим, что для доказательства свойств показательной функции, нам достаточно выбрать любую, удобную для нас последовательность рациональных чисел , сходящуюся к x. Действительно, согласно лемме ⇑, значение не зависит от выбора последовательности.

Теорема. Свойства показательной функции
Показательная функция имеет следующие свойства:
(2.0) определена, при , для всех ; ⇓
(2.1) при a ≠ 1 имеет множество значений ; ⇓
(2.2) строго возрастает при , строго убывает при , является постоянной при ; ⇓
(2.3) ; ⇓
(2.3*) ; ⇓
(2.4) ; ⇓
(2.5) ; ⇓
(2.5*) ; ⇓
(2.6) ; ⇓
(2.7) ; ⇓
(2.8) непрерывна для всех ; ⇓
(2.9) при ;

при . ⇓
Доказательство ⇓

Определение показательной функции на множестве целых чисел

Исследуем вопрос – что будет, если для функции, обладающей свойствами (1.3-5), присвоить отрицательные значения аргумента? Положим
.
Умножим это уравнение на и воспользуемся свойством (1.3):
.
Поскольку , то мы получаем:
.
Отсюда , или
.
В частности, .

Таким образом, свойства (1.3-5) выполняются для отрицательных и нулевого значения n, если положить:
;
.
Тем самым мы определили значения показательной функции для целых чисел. Однако это возможно не для всех значений основания a. Поскольку деление на нуль не возможно, то .

Определение показательной функции на множестве рациональных чисел

Теперь рассмотрим вопрос об определении показательной функции для рациональных значений аргумента. Пусть есть рациональное число. Его можно представить в виде дроби:
,
где – целое, – натуральное.

Возьмем самый простой случай. Пусть . Рассмотрим уравнение:
.
Умножим его левую и правую части на себя n раз. То есть возведем в степень n и применим свойство (1.4):
;
(3.1) .
Таким образом, есть корень степени n из a:
.
Для любого и для , существует единственное решение уравнения (3.1) в области действительных чисел (см. «Доказательство существования и единственности корня степени n»).

Далее мы используем свойства корней:
(3.2) ;
(3.3) .
(3.4) .

В силу свойства (3.2), мы можем определить значения показательной функции для рациональных значений аргумента:
.

Используя свойства (1.3-7) для целых значений аргумента и свойства корней (3.2-4), можно доказать, что (1.3-7) выполняются и для рациональных значений аргумента показательной функции.

Доказательство леммы и свойств показательной функции

Доказательство леммы

Формулировка ⇑

1. Докажем существование предела
.

Поскольку последовательность сходится, то для нее выполняется условие Коши. Это означает, что имеется такая функция , при которой для любого выполняется неравенство:
(Л.1) при .

Подставим . Тогда
(Л.2) при .

1.1. Пусть .
Докажем, что условие Коши выполняется для последовательности . Применим лемму Бернулли. При имеем:
(Л.3) .

Поскольку последовательность сходится к конечному числу, то она ограничена некоторым числом :
для всех n.
Поскольку показательная функция, определенная на множестве рациональных чисел строго возрастает при a > 1, то
для всех m.

Обозначим . В силу свойства (1.1), . Подставим в (Л.3) и применим условие Коши (Л.1). При имеем:
.
Если положить , то
при .

Итак, мы нашли такую функцию , при которой для любого ,
при .
То есть выполняется условие Коши для последовательности . Тогда на основании критерия Коши, эта последовательность сходится.

1.2. Теперь рассмотрим случай . Сведем его к предыдущему. Положим . Тогда , . Мы доказали, что последовательность сходится. Единицу в числителе можно рассматривать как элемент последовательности с постоянными членами, равными 1. Тогда, на основании арифметических свойств, существует предел частного последовательностей .

2. Теперь докажем, что предел не зависит от выбора последовательности .
То есть пусть мы имеем две, сходящиеся к x, последовательности и :
.
Мы доказали, что существуют пределы
и .
Теперь нам нужно доказать, что .

2.1. Пусть .
Рассмотрим разность последовательностей и , то есть последовательность , элементы которой равны разности элементов и . Согласно арифметическим свойствам, существует предел разности, который равен
.

Поскольку последовательности и сходятся к x, то, согласно определению предела последовательности, существуют такие функции и , так что для любого ,
при ,
при .
Положим и пусть . Тогда при имеем:
и ;
;
.
Воспользуемся тем, что конечное число членов последовательности не влияет на существование и величину предела. Отбросим первые членов у последовательностей и . Тогда
.

Применяем лемму Бернулли, аналогично предыдущему:
.
Воспользуемся свойствами пределов последовательностей, связанных неравенствами и вынесем постоянные за знак предела:
.
Применим арифметические свойства пределов:
.
Отсюда .

2.2. Пусть . Тогда ,
.
Предел последовательности не зависит от выбора . Поэтому и предел последовательности также не зависит от выбора .

Лемма доказана.

Доказательство свойств показательной функции

Формулировка ⇑

Порядок доказательств свойств показательной функции отличается от порядка, в котором расположены свойства. Это сделано для удобства изложения. Последующие пункты могут использовать свойства, доказанные в первую очередь.

2.А. Сначала докажем, что
(2.А.1) ax> 0.
Согласно определению ⇑,
.
Поскольку последовательность рациональных чисел сходится к конечному числу x, то она ограничена:
.
Поскольку функция , определенная на множестве рациональных чисел монотонна (см. (1.2) ⇑ ), то она достигает своего минимального значения на границе рассматриваемого отрезка. Тогда
(2.А.2) .
Здесь при нужно взять знак “плюс”. При – знак “минус”. При , функция постоянна, . Можно взять любой знак. Выполним в (2.А.2) предельный переход , пользуясь свойствами пределов последовательностей, связанными неравенствами и определением показательной функции ⇑:
;
.
Согласно свойству (1.1) ⇑, . Тогда и
.

2.0. ⇑ Поскольку в определении ⇑, , а аргумент x является произвольным числом и ничем не ограничен, то показательная функция определена при для всех x. Ее областью определения является множество действительных чисел .

2.6. ⇑ . Здесь аргумент является рациональным числом. Мы считаем, что свойства показательной функции на множестве рациональных чисел известны. Мы добавили пункт 2.6, чтобы объединить все свойства вместе.

2.2. ⇑ Докажем строгую монотонность показательной функции при a ≠ 1. То есть, если , то
при ;
при ;
при .

Итак, пусть . Выберем рациональные числа и , удовлетворяющие неравенствам:
.
Возьмем последовательности и , сходящиеся к и :
,
элементы которых удовлетворяют неравенствам:
, .
Тогда
.

2.2.1. Пусть .
Поскольку показательная функция, определенная на множестве рациональных чисел, при , строго возрастает, то
(2.2.1) .
Применим свойства пределов последовательностей, связанных неравенствами и определение показательной функции ⇑:
;
.
Отсюда .

2.2.2. Пусть .
В этом случае, показательная функция, определенная на множестве рациональных чисел, строго убывает. Доказательство такое же, как и в пункте 2.2.1, только начиная с (2.2.1), нужно поменять знаки неравенств:
(2.2.2) ;
;
;
.

2.2.3. Пусть .
Показательная функция , определенная на множестве рациональных чисел , является постоянной . Последовательность является последовательностью из постоянных элементов. Поэтому ее предел также равен единице:
;
для всех x.

2.3. ⇑ Докажем, что
.
Пусть и – произвольные последовательности рациональных чисел, сходящиеся к и :
.
Применим свойство предела суммы для последовательности :
(2.3.1) .
Рассмотрим последовательность . Поскольку, согласно лемме ⇑, и сходятся, то применим свойство предела произведения последовательностей иопределение показательной функции ⇑:
.
С другой стороны, применяя (2.3.1) и свойство (1.3) ⇑ показательной функции от рационального аргумента, имеем:
.
Отсюда
.

2.5. ⇑ Докажем, что
.
Все рассуждения и обозначения такие же, что и при доказательстве свойства (2.3) ⇑. Аналогичным образом, применяя свойство (1.5) ⇑ для рационального аргумента, имеем:
.

2.7. ⇑ Докажем, что
.
Аналогично предыдущему, имеем:
.
Здесь мы учли, что и применили свойство предела частного последовательностей.

2.3*. ⇑ Применяя свойства (2.3) ⇑ и (2.7) ⇑, имеем:
.

2.8. ⇑ Докажем непрерывность показательной функции.
2.8.1. Пусть .

Воспользуемся определением непрерывности функции в терминах приращений. Применяем свойство ax> 0 ⇑ и (2.3) ⇑
.
Поскольку есть сколь угодно малая величина, то считаем, что . Применим лемму Бернулли для действительных чисел:
.
Тогда
.
Применяем свойство пределов функций, связанных неравенством:
;
;
.

2.4. ⇑ Докажем, что
.

2.4.1. Рассмотрим случай .
Пусть – натуральные числа. Тогда
.
Применяя свойство (2.3) ⇑, имеем:
;
(2.4.1) .

Теперь исследуем, что такое . Введем обозначение:
(2.4.2) .
Возведем в n-ю степень. То есть умножим левую и правую части на себя n раз, и применим (2.4.1):
;
.
Поскольку ax> 0 ⇑, то b есть корень степени n из положительного числа :
. Подставляя (2.4.2), имеем:
(2.4.3) .

Применяя свойства (2.4.1) и (2.4.3), для произвольного положительного рационального числа получаем:
;
(2.4.4) .

Пусть есть произвольная последовательность рациональных чисел, сходящаяся к x2:
(2.4.5) .
Применяя (2.4.4), имеем:
.
Рассмотрим последовательность . Учитывая (2.4.5), и применяя арифметические свойства сходящихся последовательностей, получаем, что сходится к :
.
Выше мы доказали, что показательная функция непрерывна ⇑. Используя определение непрерывности функции по Гейне, получаем:
;
.

2.4.2. Рассмотрим случай .
Тогда . Применяя свойство (2.7) ⇑, имеем:
.

2.4.3. Теперь пусть .
Применяем (2.6) ⇑ Тогда .
Поскольку ax1> 0 ⇑, то
;
.

2.5*. ⇑ Докажем, что
.
Применяя свойства (2.7) ⇑, (2.5) ⇑ и (2.4) ⇑, имеем:
.

2.9. ⇑
2.9.1. Пусть .
2.9.1.1. Докажем, что
.
Поскольку функция монотонна ⇑, то согласно теореме о пределе монотонной функции, она имеет конечный или бесконечный предел
.
Поскольку функция имеет предел A, то согласно определению предела функции по Гейне, для любой последовательности , сходящейся к , последовательность сходится к A:
.
Возьмем последовательность натуральных чисел . Она сходится к : . Тогда
.

Для вычисления этого предела, применим неравенство Бернулли:
.
При , правая часть неравенства стремится к . Применяя свойство неравенств бесконечно больших последовательностей, находим, что
.
Отсюда , .

2.9.1.2. Докажем, что
.
Сделаем подстановку . Применим свойство (2.7) ⇑ и свойства бесконечно малых и бесконечно больших функций:
.

2.9.2. Пусть .
Сделаем подстановку . Тогда ,
;
.

2.1. ⇑ Докажем, что при a ≠ 1 показательная функция имеет множество значений .
Рассмотрим функцию на отрезке , где – произвольные числа. Поскольку функция строго монотонна ⇑ и определена для всех x, то она достигает минимума и максимума на концах отрезка – в точках и . Поскольку функция непрерывна ⇑, то согласно теореме Больцано – Коши о промежуточном значении, она принимает все значения из отрезка , если и , если . Устремляя и , и используя найденные выше пределы ⇑ получаем, что множеством значений показательной функции является множество положительных чисел .

Теорема доказана.

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Автор: Олег Одинцов. Опубликовано: 17-11-2018 Изменено: 02-01-2019

Источник

Показательная функция

Функция вида y = ax, где a больше нуля и а не равно единице называется показательной функцией. Основные свойства показательной функции:

1. Областью определения показательной функции будет являться множество вещественных чисел.

2. Область значений показательной функции будет являться множество всех положительных вещественных чисел. Иногда это множество для краткости записи обозначают как R+.

3. Если в показательной функции основание a больше единицы, то функция будет возрастающей на всей области определения. Если в показательной функции для основания а выполнено следующее условие 0

4. Справедливы будет все основные свойства степеней. Основные свойства степеней представлены следующим равенствами:

ax*ay = a(x + y);

(ax)/(ay) = a(x-y);

(a*b)x = (ax)*(ay);

(a/b)x = ax/bx;

(ax)y = a(x * y).

Данные равенства будут справедливы для все действительных значений х и у.

5. График показательной функции всегда проходит через точку с координатами (0;1)

6. В зависимости от того возрастает или убывает показательная функция, её график будет иметь один из двух видов.

На следующем рисунке представлен график возрастающей показательной функции: a>0.

На следующем рисунке представлен график убывающей показательной функции: 0

И график возрастающей показательной функции и график убывающей показательной функции согласно свойству, описанному в пятом пункте, проходят через точку (0;1).

7. Показательная функция не имеет точек экстремума, то есть другими словами, она не имеет точек минимума и максимума функции. Если рассматривать функцию на каком-либо конкретном отрезке, то минимальное и максимальное значения функция будет принимать на концах этого промежутка.

8. Функция не является четной или нечетной. Показательная функция это функция общего вида. Это видно и из графиков, ни один из них не симметричен ни относительно оси Оу, ни относительно начала координат.

Логарифм

Что такое логарифм

Логарифмы всегда считались сложной темой в школьном курсе математики. Существует много разных определений логарифма, но большинство учебников почему-то используют самые сложные и неудачные из них.

Мы же определим логарифм просто и наглядно. Для этого составим таблицу:

Итак, перед нами степени двойки. Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число. Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.

А теперь — собственно, определение логарифма:

Определение

Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a, чтобы получить число x.

Обозначение

loga x = b
где a — основание, x — аргумент, b — собственно, чему равен логарифм.

Например, 23 = 8 ⇒ log2 8 = 3 (логарифм по основанию 2 от числа 8 равен трем, поскольку 23 = 8). С тем же успехом log2 64 = 6, поскольку 26 = 64.

Операцию нахождения логарифма числа по заданному основанию называют логарифмированием. Итак, дополним нашу таблицу новой строкой:

log2 2 = 1

log2 4 = 2

log2 8 = 3

log2 16 = 4

log2 32 = 5

log2 64 = 6

К сожалению, далеко не все логарифмы считаются так легко. Например, попробуйте найти log2 5. Числа 5 нет в таблице, но логика подсказывает, что логарифм будет лежать где-то на отрезке [2; 3]. Потому что 22 < 5 < 23, а чем больше степень двойки, тем больше получится число.

Если взять калькулятор и посчитать, чему равны такие логарифмы, то получатся очень длинные числа. Взгляните сами:
log2 5 = 2,32192809…
log3 8 = 1,89278926…
log5 100 = 2,86135311…

Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Если логарифм получается иррациональным, его лучше так и оставить: log2 5, log3 8, log5 100.

Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:

Перед нами — не что иное как определение логарифма. Вспомните: логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.

Как считать логарифмы

С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:

Аргумент и основание всегда должны быть больше нуля. Это следует из определения степени рациональным показателем, к которому сводится определение логарифма.
Основание должно быть отличным от единицы, поскольку единица в любой степени все равно остается единицей. Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла. Нет такой степени!

Такие ограничения называются областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: loga x = b ⇒ x > 0, a > 0, a ≠ 1.

Заметьте, что никаких ограничений на число b (значение логарифма) не накладывается. Например, логарифм вполне может быть отрицательным: log2 0,5 = −1, т.к. 0,5 = 2−1.

Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.

Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов:

Представить основание a и аргумент x в виде степени с минимально возможным основанием, большим единицы. Попутно лучше избавиться от десятичных дробей;
Решить относительно переменной b уравнение: x = ab;
Полученное число b будет ответом.

Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.

Посмотрим, как работает эта схема на конкретных примерах:

Задача

Вычислите логарифм: log5 25

Решение

Представим основание и аргумент как степень пятерки: 5 = 51; 25 = 52;
Составим и решим уравнение:
log5 25 = b ⇒ (51)b = 52 ⇒ 5b = 52 ⇒ b = 2;
Получили ответ: 2.

Ответ

Задача

Вычислите логарифм:

Решение

Представим основание и аргумент как степень тройки: 3 = 31; 1/81 = 81−1 = (34)−1 = 3−4;
Составим и решим уравнение:

Получили ответ: −4.

Ответ

−4

Задача

Вычислите логарифм: log4 64

Решение

Представим основание и аргумент как степень двойки: 4 = 22; 64 = 26;
Составим и решим уравнение:
log4 64 = b ⇒ (22)b = 26 ⇒ 22b = 26 ⇒ 2b = 6 ⇒ b = 3;
Получили ответ: 3.

Ответ

Задача

Вычислите логарифм: log16 1

Решение

Представим основание и аргумент как степень двойки: 16 = 24; 1 = 20;
Составим и решим уравнение:
log16 1 = b ⇒ (24)b = 20 ⇒ 24b = 20 ⇒ 4b = 0 ⇒ b = 0;
Получили ответ: 0.

Ответ

Задача

Вычислите логарифм: log7 14

Решение

Представим основание и аргумент как степень семерки: 7 = 71; 14 в виде степени семерки не представляется, поскольку 71 < 14 < 72;
Из предыдущего пункта следует, что логарифм не считается;
Ответ — без изменений: log7 14.

Ответ

log7 14

Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. Если в разложении есть хотя бы два различных множителя, число не является точной степенью.

Задача

Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14.

Решение

8 = 2 · 2 · 2 = 23 — точная степень, т.к. множитель всего один;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 24 — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 34 — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;

Ответ

8, 81 — точная степень; 48, 35, 14 — нет.

Заметим также, что сами простые числа всегда являются точными степенями самих себя.

Десятичный логарифм

Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.

Определение

Десятичный логарифм от аргумента x — это логарифм по основанию 10, т.е. степень, в которую надо возвести число 10, чтобы получить число x.

Обозначение

lg x

Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д.

Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать:
lg x = log10 x

Все, что верно для обычных логарифмов, верно и для десятичных.

Натуральный логарифм

Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.

Определение

Натуральный логарифм от аргумента x — это логарифм по основанию e, т.е. степень, в которую надо возвести число e, чтобы получить число x.

Обозначение

ln x

Многие спросят: что еще за число e? Это иррациональное число, его точное значение найти и записать невозможно. Приведу лишь первые его цифры:
e = 2,718281828459…

Не будем углубляться, что это за число и зачем нужно. Просто помните, что e — основание натурального логарифма:
ln x = loge x

Таким образом, ln e = 1; ln e2 = 2; ln e16 = 16 — и т.д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.

Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.

Основные свойства логарифмов

Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать. Но поскольку логарифмы — это не совсем обычные числа, здесь есть свои правила, которые называются основными свойствами.

Эти правила обязательно надо знать — без них не решается ни одна серьезная логарифмическая задача. К тому же, их совсем немного — все можно выучить за один день. Итак, приступим.

Сложение и вычитание логарифмов

Рассмотрим два логарифма с одинаковыми основаниями: loga x и loga y. Тогда их можно складывать и вычитать, причем:

loga x + loga y = loga (x · y);
loga x − loga y = loga (x : y).

Итак, сумма логарифмов равна логарифму произведения, а разность — логарифму частного. Обратите внимание: ключевой момент здесь — одинаковые основания. Если основания разные, эти правила не работают!

Эти формулы помогут вычислить логарифмическое выражение даже тогда, когда отдельные его части не считаются (см. урок «Что такое логарифм»). Взгляните на примеры — и убедитесь:

Задача

Найдите значение выражения: log6 4 + log6 9.

Решение

Поскольку основания у логарифмов одинаковые, используем формулу суммы:
log6 4 + log6 9 = log6 (4 · 9) = log6 36 = 2.

Ответ

Задача

Найдите значение выражения: log2 48 − log2 3.

Решение

Основания одинаковые, используем формулу разности:
log2 48 − log2 3 = log2 (48 : 3) = log2 16 = 4.

Ответ

Задача

Найдите значение выражения: log3 135 − log3 5.

Решение

Снова основания одинаковые, поэтому имеем:
log3 135 − log3 5 = log3 (135 : 5) = log3 27 = 3.

Ответ

Как видите, исходные выражения составлены из «плохих» логарифмов, которые отдельно не считаются. Но после преобразований получаются вполне нормальные числа. На этом факте построены многие контрольные работы. Да что контрольные — подобные выражения на полном серьезе (иногда — практически без изменений) предлагаются на ЕГЭ.

Вынесение показателя степени из логарифма

Теперь немного усложним задачу. Что, если в основании или аргументе логарифма стоит степень? Тогда показатель этой степени можно вынести за знак логарифма по следующим правилам:

loga xn = n · loga x;

Несложно заметить, что последнее правило следует их первых двух. Но лучше его все-таки помнить — в некоторых случаях это значительно сократит объем вычислений.

Разумеется, все эти правила имеют смысл при соблюдении ОДЗ логарифма: a > 0, a ≠ 1, x > 0. И еще: учитесь применять все формулы не только слева направо, но и наоборот, т.е. можно вносить числа, стоящие перед знаком логарифма, в сам логарифм. Именно это чаще всего и требуется.

Задача

Найдите значение выражения: log7 496.

Решение

Избавимся от степени в аргументе по первой формуле:
log7 496 = 6 · log7 49 = 6 · 2 = 12

Ответ

Задача

Найдите значение выражения:

Решение

Заметим, что в знаменателе стоит логарифм, основание и аргумент которого являются точными степенями: 16 = 24; 49 = 72. Имеем:

Преобразование частного двух логарифмов

Ответ

Думаю, к последнему примеру требуются пояснения. Куда исчезли логарифмы? До самого последнего момента мы работаем только со знаменателем. Представили основание и аргумент стоящего там логарифма в виде степеней и вынесли показатели — получили «трехэтажную» дробь.

Теперь посмотрим на основную дробь. В числителе и знаменателе стоит одно и то же число: log2 7. Поскольку log2 7 ≠ 0, можем сократить дро