Какими свойствами обладает объем фигуры

ВОПРОСЫ
1. Какими свойствами обладает объем фигуры?
1) Равные фигуры имеют равные объемы.
2) Объем фигуры равен сумме объемов фигур, из которых она состоит.
2. Какой куб называют единичным?
Единичный куб — это куб, ребро которого равно единице измерения отрезков.
3. Приведите примеры единиц измерения объема.

4. Что означает измерить объем фигуры?
Измерить объем фигуры — значит подсчитать, сколько единичных кубов в ней помещается.
5. Чему равен объем прямоугольного параллелепипеда с измерениями а, b, c?

6. По какой формуле вычисляется объем куба?

7. Как вычислить объем прямоугольного параллелепипеда, зная его площадь основания и высоту?

РЕШАЕМ УСТНО
1. Заполните пропуски в цепочки вычислений:

2. Сколько необходимо использовать кубиков с ребром 1 см, сложить кубик с ребром 2 см?
Нужно взять 8 кубиков с ребром 1 см.
3. Сколько сантиметров проволоки необходимо для изготовления проволочного каркаса прямоугольного параллелепипеда, измерения которого равны 3 см, 5 см и 6 см?

4. Расставьте вместо звездочек знаки «+» и » — » так, чтобы запись 20 * 30 * 10 * 80 * 70 = 50 стала верным равенством.
20+30-10+80-70=50.
УПРАЖНЕНИЯ
617. 1) Сколько сантиметров в одном дециметре? Квадратных сантиметров в одном квадратном дециметре? Кубических сантиметров в одном кубическом дециметре?
2) Сколько сантиметров в одном метре? Квадратных сантиметров в одном квадратном метре? Кубических сантиметров в одном кубическом метре?

618. Фигуры, изображенные на рисунке 179, сложены из кубиков, ребра которых равны 1 см. Найдите объем каждой фигуры.

619. Вычислите объем прямоугольного параллелепипеда, измерения которого равны 12 м, 15 м и 6 м.

620. Чему равен объем куба, ребро которого равно 6 см?

621. Чему равен объем прямоугольного параллелепипеда с измерениями 10 дм, 8 дм и 4 дм?

622. Выразите:
1) в кубических миллиметрах: 7 см3, 38 см3; 12 см3 243 мм3; 42 см3 68 мм3; 54 см3 4 мм3; 1 дм3 20 мм3; 18 дм3 172 см3; 35 дм3 67 см3 96 мм3;
2) в кубических дециметрах: 4 м3; 264 м3; 10 м3 857 дм3; 28 м3 2 дм3; 44 000 см3; 5 430 000 см3.


623. Выразите в кубических сантиметрах: 8 дм3; 62 дм3; 378 000 мм3; 520 000 мм3; 78 дм3 325 см3; 56 дм3 14 см3; 8 м3 4 дм3 6 см3.

624. Ширина прямоугольного параллелепипеда равна 15 дм, длина — на 3 дм больше ширины, а высота в 3 раза меньше длины. Найдите объем данного параллелепипеда.

625. Высота прямоугольного параллелепипеда равна 20 см, что на 4 см меньше его длины и в 5 раз больше его ширины. Вычислите объем данного параллелепипеда.

626. Объем прямоугольного параллелепипеда равен 560 см3, длина — 14 см, ширина — 8 см. Найдите высоту данного параллелепипеда.

627. Длина прямоугольного параллелепипеда равна 18 см, высота — 15 см, а объем — 3 240 см3. Найдите ширину данного параллелепипеда.

628. Объем комнаты, имеющей форму прямоугольного параллелепипеда, равен 144 м3, а высота — 4 м. Найдите площадь пола комнаты.

629. Спортивный зал имеет форму прямоугольного параллелепипеда, его объем равен 960 м3, а площадь пола равна 192 м2. Найдите высоту спортивного зала.

630. Найдите объем фигуры, изображенной на рисунке 180 (размеры даны в сантиметрах).

631. Найдите объем фигуры, изображенной на рисунке 181 (размеры даны в сантиметрах).


632. Ребро куба, изготовленного из цинка, равно 4 см. Найдите массу куба, если 1 см3 цинка составляет 7 г.

633. Знайка сконструировал землеройную машину, которая за 8 ч может вырыть траншею, имеющую форму прямоугольного параллелепипеда, длиной 150 м, глубиной 80 см и шириной 60 см. Сколько кубометров земли выкапывает эта машина за 1 ч? Работу скольких коротышек выполняет эта машина, если за 8 ч один коротышка может выкопать 240 дм3 земли?

634. Куб и прямоугольный параллелепипед имеют равные объемы. Найдите площади поверхности куба, если длина прямоугольного параллелепипеда равна 12 см, что в 2 раза больше ширины и в 4 раза больше высоты параллелепипеда.

635. Ребро одного куба в 4 раза больше ребра второго. Во сколько раз: 1) площадь поверхности первого куба больше площади поверхности второго; 2) объем первого куба больше объема второго?

636. Как изменится объем прямоугольного параллелепипеда, если: 1) длину увеличить в 4 раза, ширину — в 2 раза, высоту в 5 раз; 2) ширину уменьшить в 4 раза, высоту в 2 раза, а длину увеличить в 16 раз?

637. Как изменится объем прямоугольного параллелепипеда, если: 1) каждое измерение увеличить в 2 раза; 2) длину уменьшить в 3 раза, высоту — в 5 раз, а ширину увеличить в 15 раз?

638. В бассейн, площадь которого равна 1 га, налили 1 000 000 л воды. Можно ли в этом бассейне провести соревнования по плаванию?

639. В кубе с ребром 3 см проделали три сквозных квадратных отверстия со стороной 1 см (рис. 182). Найдите объем оставшейся части.

640. Размеры куска мыла, имеющего форму прямоугольного параллелепипеда, равны 12 см, 6 см и 4 см. Каждый день используют одинаковую массу мыла. Через 14 дней все размеры куска мыла уменьшились в 2 раза. На сколько дней хватит оставшегося куска мыла?

УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
641. В школьном коридоре, длина которого равна 30 м, ширина — 35 дм, надо заменить линолеум. Какое наименьшее количество рулонов линолеума для этого нужно, если длина рулона линолеума равна 12 м, а ширина — 160 см?

642. Из двух населенных пунктов, расстояние между которыми равно 54 км, одновременно выехали навстречу друг другу и встретились через 2 ч после начала движения. Скорость движения первого велосипедиста составляла 12 км/ч. С какой скоростью двигался второй велосипедист?

643. Найдите значение выражения:


ЗАДАЧА ОТ МУДРОЙ СОВЫ
644. В записи первого трехзначного числа используются только цифры 2 и 3, а в записи второго — только цифры 3 и 4. Может ли произведение этих чисел записываться только цифрами 2 и 4?
![]()
Геометрия, 11 класс
Урок №11
Понятие объёма
Перечень вопросов, рассматриваемых на уроке:
Понятие объёма.
Свойства объёмов.
Объём прямоугольного параллелепипеда.
Формула объёма прямоугольного параллелепипеда.
Тезаурус
Объём тела– величина, характеризующая часть пространства, занимаемую телом, и определяемая формой и линейными размерами этого тела.
Основные свойства объёма:
— равные тела имеют равные объёмы;
— если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.
Основная литература:
Атанасян Л. С. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы [текст]: учеб. для общеобразоват. организаций: базовый и углубл. уровни – М.: Просвещение, 2014. – 255 с. С. 130–133.
Теоретический материал для самостоятельного изучения
С понятием объёмного тела, отличающегося от плоской фигуры, мы познакомились ещё в начальной школе.
Объёмом принято называть положительную величину, характеризующую часть пространства, занимаемую телом, и определяемую формой и линейными размерами этого тела.
Мы можем вычислить объём тела точно так же, как ранее находили площадь фигуры. Объём принято измерять в единицах измерения объёма (единицах измерения размера пространства, занимаемого телом), то есть в кубических метрах, сантиметрах, миллиметрах и так далее. За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (обозначение: см3). По аналогии, можно за единицу измерения объёма принять кубический миллиметр (1 мм3), кубический метр (1 м3) и тому подобное.
Объём выражается в положительных числах. Это число показывает, сколько единиц измерения содержится в теле. Например, сколько кубических миллиметров в аквариуме, сколько кубических метровв бассейне и так далее.
Объём обозначается заглавной латинской буквой V.
Пример:
Объём книги400 кубических сантиметров запишут: V = 400см3.
Рассмотрим свойства объёмов.
Свойство № 1. Равные тела имеют равные объёмы. Это означает, что если два тела идентичны, то есть имеют равное количество единиц измерения и частей, то равны и их объёмы. Например, 2 одинаковых пакета молока равны в объёме.
Свойство № 2. Если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.
Следствие из основных свойств объёмов.
Объём куба с ребром 1/n равен 1/n3
Доказательство. Рассмотрим куб, объём которого принят за единицу измерения объёмов, тоесть равный некоторому числукубических сантиметров. Его ребро равно единице измерения отрезков. Разобьём каждое ребро этого куба на произвольное количество частей – nтак, чтобы провести плоскости, перпендикулярные к этому ребру.

По второму свойству объёмов, сумма объёмов всех кубиков равна объёму всего куба (1 см3). Следовательно, поскольку мы разбили каждое ребро на n частей, то каждый маленький куб внутри большого куба будет иметь ребро

Объём каждого из маленьких кубиков при этом будет равен 1/n3.
Объём прямоугольного параллелепипеда
Теорема
Объём прямоугольного параллелепипеда равен произведению трёх его измерений.
Доказательство
Обозначимизмеренияпрямоугольного параллелепипеда P буквами a,b,c, его объём буквой V, и докажем, что V = a ∙ b ∙ c.

Рассмотрим два возможных случая.
Случай первый. Измерения a, b и c представляют собой конечные десятичные дроби, у которых число знаков после запятой не превосходит n (можно считать, что n больше или равно 1). В этом случае числа a ∙10n, b∙10n, c∙10n, являются целыми. Разобьём каждое ребро параллелепипеда на равные части длины: 1/10n и через точки разбиения проведём плоскости, перпендикулярные к этому ребру. Параллелепипед P разобьётся на abc∙103n равных кубов с ребром 1/10n. Так как объём каждого куба равен 1/103n, что мы доказали ранее, то объём всего параллелепипеда P = abc, что и требовалось доказать.
Случай второй.
Хотя бы одно из измерений a, b, c представляет собой бесконечную десятичную дробь. Рассмотрим конечные десятичные дроби: an, bn, cn, которые получаются из чисел a, b, c, если отбросить в каждом из них все цифры после запятой, начиная с n + 1. Очевидно, an ≤ a ≤ an’, где an’ = an+1 : 10n. Аналогичные неравенства справедливы для b и c. Перемножив эти неравенства, получим произведение anbncn ≤ abc ≤ an’bn’cn’, где bn’= bn+1 : 10n, cn’ = cn+1 : 10n
По доказанному в первом случае, левая часть неравенства представляет собой объём Vn прямоугольного параллелепипеда Pn с измерениями an, bn, cn, а правая часть – это объём Vn’ прямоугольного параллелепипеда Pn’ с измерениями an’, bn’, cn’. Так как параллелепипед P содержит в себе параллелепипед Pn, а сам содержится в параллелепипеде Pn’, то объём V параллелепипеда P заключён между Vn, = anbncn и Vn’= an’bn’cn’. Будем неограниченно увеличивать n. Тогда 1/10n будет становиться сколь угодно малым, и поэтому произведение an’bn’cn’ будет сколь угодно мало отличаться от числа, выраженного произведением anbncn. Отсюда следует, что число V сколь угодно мало отличается от числа, выраженного произведением anbncn, а значит, они равны.V = abc, что и требовалось доказать.
Примеры и разбор решения заданий тренировочного модуля.
№1.Длины сторон основания прямоугольного параллелепипеда равны 15 см и 20 см. Высота параллелепипеда равна диагонали основания. Найдите объём этого параллелепипеда.
Решение:
Найдём длину диагонали основания, для этого воспользуемся теоремой Пифагора:

А теперь найдём объём параллелепипеда:
V = 15 ∙ 20 ∙ 25 = 7500 см3
Ответ: V = 7500 см3.
 №2.
№2.
Найдите площадь закрашенной фигуры, если объём прямоугольного параллелепипеда равен 960 см3, AB = 8 см, АА1= 20 см.
Варианты ответов:
220 см2
100 см2
400 см2
200 см2
Решение.
Найдём длину АD:
AD = 960 : 8 : 20 = 6 см
Найдём АС, воспользовавшись теоремой Пифагора:

Закрашенная фигура – прямоугольник. Вычислим его площадь: 10∙20= 200 см2.
Ответ: площадь закрашенной фигуры 200 см2.
Верный ответ: 200 см2.
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
1. Какими свойствами обладает объём фигуры?
- Равные фигуры имеют равные объёмы.
- Объём фигуры равен сумме объёмов фигур, из которых она состоит.
2. Какой куб называют единичным?
Единичным называют куб, ребро которого равно единичному отрезку.
3. Приведите примеры единиц измерения объёма.
- 1 мм³ — один кубический миллиметр
- 1 см³ — один кубический сантиметр
- 1 дц³ — один кубический дециметр
- 1 м³ — один кубический метр
- 1 л — один литр (при измерении жидкостей, 1 л = 1 дм³)
4. Что означает измерить объём фигуры?
Измерить объем фигуры — значит подсчитать, сколько единичных кубов в ней помещается.
5. Чему равен объём прямоугольного параллелепипеда с измерениями а, b, с?
V = abc
6. По какой формуле вычисляют объём куба?
V= a³
7. Как вычислить объём прямоугольного параллелепипеда, зная его площадь основания и высоту?
V = Sh
Решаем устно
1. Заполните пропуски в цепочке вычислений:

2. Сколько необходимо использовать кубиков с ребром 1 см, чтобы сложить кубик с ребром 2 см?
Чтобы сложить кубик с ребром 2 см, надо использовать 8 кубиков с ребром 1 см.

3. Сколько сантиметров проволоки необходимо для изготовления проволочного каркаса прямоугольного параллелепипеда, измерения которого равны 3 см, 5 см и 6 см?
3 • 4 + 5 • 4 + 6 • 4 = 12 + 20 + 24 = 56 (см) — проволоки.
Ответ: 56 см.
4. Расставьте вместо звёздочек знаки «+» и «—» так, чтобы запись 20 * 30 * 10 * 80 * 70 = 50 стала верным равенством.
20 + 30 — 10 + 80 — 70 = (20 + 30) + (80 — 10 — 70) = 50 + 0 = 50
Упражнения
617. 1) Сколько сантиметров в одном дециметре? Квадратных сантиметров в одном квадратном дециметре? Кубических сантиметров в одном кубическом дециметре?
- 1 дм = 10 см
- 1 дм² = 10 см • 10 см = 100 см²
- 1 дм³ = 10 см • 10 см • 10 см = 1 000 см³
2) Сколько сантиметров в одном метре? Квадратных сантиметров в одном квадратном метре? Кубических сантиметров в одном кубическом метре?
- 1 м = 100 см
- 1 м² = 100 см • 100 см = 10 000 см²
- 1 м³ = 100 см • 100 см • 100 см = 1 000 000 см³
618. Фигуры, изображённые на рисунке 179, сложены из кубиков, рёбра которых равны 1 см. Найдите объём каждой фигуры.
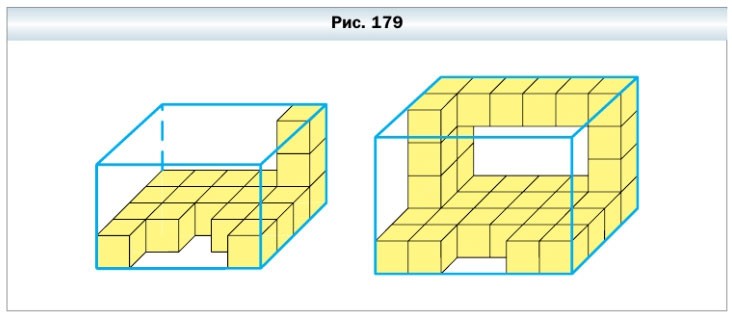
Для того, чтобы найти объём фигуры, надо посчитать количество единичных кубов, из которых она состоит.
1 фигура (на рисунке слева):
V = 5 • 2 + 3 + 3 + 2 = 10 + 8 = 18 см³
2 фигура (на рисунке справа):
V = 6 • 3 + 2 +2 + 3 • 2 + 5 + 2 = 18 + 4 + 6 + 7 = 18 + 17 = 35 см³
Ответ: 18 см³ и 35 см³.
619. Вычислите объём прямоугольного параллелепипеда, измерения которого равны 12 м, 15 м и 6 м.
Дано:
a = 12 м
b = 15 м
c = 6 м
V = ? м³

Решение:
V = abc = 12 • 15 • 6 = 12 • 90 = 1 080 м³
Ответ: 1 080 м³.
620. Чему равен объём куба, ребро которого равно 6 см?
Дано:
a = 12 см
V = ? см³
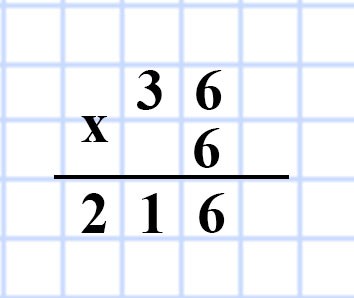
Решение:
V= a³ = 6³ = 36 • 6 = 216 см³
Ответ: 216 см³.
621. Чему равен объём прямоугольного параллелепипеда с измерениями 10 дм, 8 дм и 4 дм?
Дано:
a = 10 дм
b = 8 дм
c = 4 дм
V = ? дм³
Решение:
V = abc = 10 • 8 • 4 = 10 • 32 = 320 дм³
Ответ: 320 дм³.
622. Выразите:
1) в кубических миллиметрах:
7 см³ = 7 000 мм³
38 см³ = 38 000 мм³
12 см³ 243 мм³ = 12 000 мм³ + 243 мм³ = 12 243 мм³
42 см³ 68 мм³ = 42 000 мм³ + 68 мм³ = 42 068 мм³
54 см³ 4 мм³; = 54 000 мм³ + 4 мм³ = 54 004 мм³
1 дм³ 20 мм³ = 1 000 000 мм³ + 20 мм³ = 1 000 020 мм³
18 дм³ 172 см³ = 18 000 000 мм³ + 172 000 мм³ = 18 172 000 мм³
35 дм³ 67 см³ 96 мм³ = 35 000 000 мм³ + 67 000 мм³ + 96 мм³ = 35 067 096 мм³
2) в кубических дециметрах:
4 м³ = 4 000 дм³
264 м³ = 264 000 дм³
10 м³ 857 дм³ = 10 000 дм³ + 857 дм³ = 10 857 дм³
28 м³ 2 дм³ = 28 000 дм³ + 2 дм³ = 28 002 дм³
44 000 см³ = 44 дм³
5 430 000 см³ = 5 430 дм³
623. Выразите в кубических сантиметрах:
8 дм³ = 8 000 см³
62 дм³ = 62 000 см³
378 000 мм³ = 378 см³
520 000 мм³ = 520 см³
78 дм³ 325 см³ = 78 000 см³ + 325 см³ = 78 325 см³
56 дм³ 14 см³ = 56 000 см³ + 14 см³ = 56 014 см³
8 м³ 4 дм³ 6 см³ = 8 000 000 см³ + 4 000 см³ + 6 см³ = 8 004 006 см³
624. Ширина прямоугольного параллелепипеда равна 15 дм, длина — на 3 дм больше ширины, а высота — в 3 раза меньше длины. Найдите объём данного параллелепипеда.
Дано:
a = ? см, на 3 дм больше, чем ребро b
b = 15 дм
c = ? см, в 3 раза меньше, чем ребро a
V = ? см³
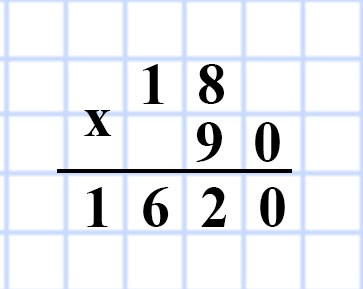
Решение:
1) 15 + 3 = 18 (дм) — длина прямоугольного параллелепипеда.
2) 18 : 3 = 6 (дм) — высота прямоугольного параллелепипеда.
V = abc
3) 18 • 15 • 6 = 18 • 90 = 1 620 (дм³) — объем V прямоугольного параллелепипеда.
Ответ: V= 1 620 дм³.
625. Высота прямоугольного параллелепипеда равна 20 см, что на 4 см меньше его длины и в 5 раз больше его ширины. Вычислите объём данного параллелепипеда.
Дано:
a = ? см, на 4 см больше, чем ребро с
b = ? см, в 5 раз меньше, чем ребро c
c = 20 см
V = ? см³
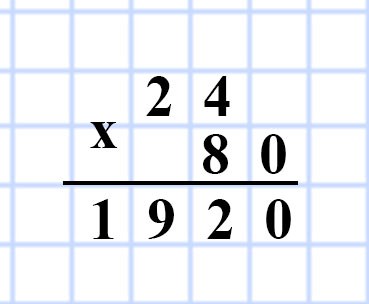
Решение:
1) 20 + 4 = 24 (см) — длина прямоугольного параллелепипеда.
2) 20 : 5 = 4 (см) — ширина прямоугольного параллелепипеда.
V = abc
3) 24 • 5 • 20 = 24 • 80 = 1 920 (дм³) — объем V прямоугольного параллелепипеда.
Ответ: V= 1 920 дм³.
626. Объём прямоугольного параллелепипеда равен 560 см³, длина — 14 см, ширина — 8 см. Найдите высоту данного параллелепипеда.
Дано:
a = 14 см
b = 8 см
V = 560 см³
h = ? см
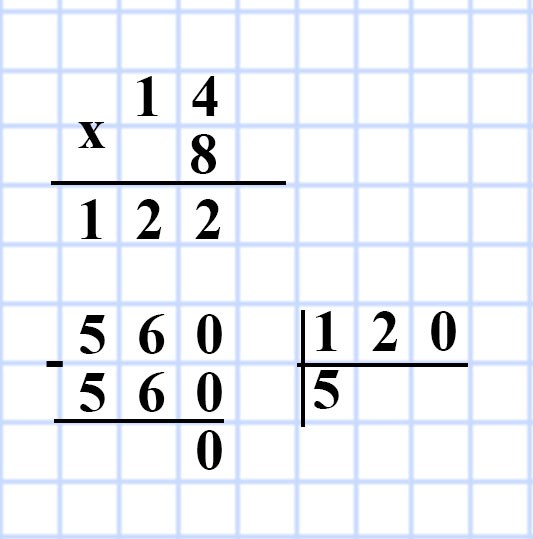
Решение:
V = Sh, значит h = V : S
1) 14 • 8 = 122 (см²) — площадь основания S прямоугольного параллелепипеда.
2) 560 : 120 = 5 (см) — высота h прямоугольного параллелепипеда.
Ответ: 5 см.
627. Длина прямоугольного параллелепипеда равна 18 см, высота — 15 см, а объём — 3 240 см³. Найдите ширину данного параллелепипеда.
Дано:
a = 18 см
h = 15 см
V = 3 240 см³
b = ? см
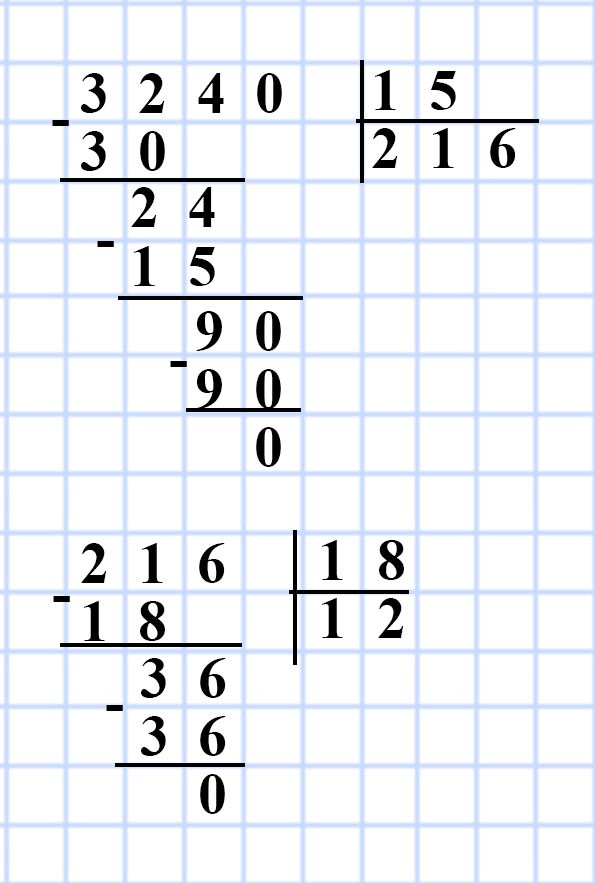
Решение:
V = Sh, значит S = V : h
1) 3 240 : 15 = 216 (см²) — площадь основания S прямоугольного параллелепипеда.
S = a • b, значит b = S : a
2) 216 : 18 = 12 (см) — ширина b прямоугольного параллелепипеда.
Ответ: 12 см.
628. Объём комнаты, имеющей форму прямоугольного параллелепипеда, равен 144 м³, а высота — 4 м. Найдите площадь пола комнаты.
Дано:
h = 4 м
V = 144 м³
S = ? м²
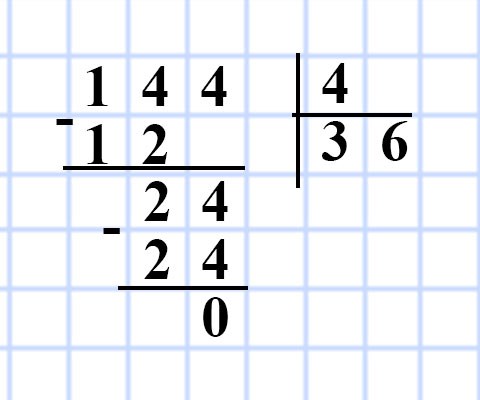
Решение:
V = Sh, значит S = V : h
1) 144 : 4 = 36 (м²) — площадь пола комнаты.
Ответ: 36 м².
629. Спортивный зал имеет форму прямоугольного параллелепипеда, его объём равен 960 м³, а площадь пола равна 192 м². Найдите высоту спортивного зала.
Дано:
S = 192 м²
V = 960 м³
h= ? м

Решение:
V = Sh, значит h = V : S
1) 960 : 192 = 5 (м) — высота спортивного зала.
Ответ: 5 м.
630. Найдите объём фигуры, изображённой на рисунке 180 (размеры даны в сантиметрах).
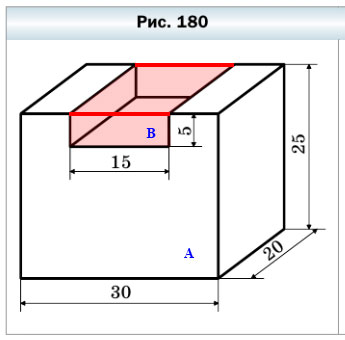
Выполним дополнительное построение: проведём линии, соединяющие выступающие части исходной фигуры. Теперь можно сказать, что V = VА— VВ, где:
- V — объем искомой фигуры.
- VА — объем большого прямоугольного параллелепипеда, измерения которого равны 30 см, 20 см и 25 см.
- VВ — объем малого прямоугольного параллелепипеда (красный), который вырезали из большого параллелепипеда для получения искомой фигуры. Его измерения: 15 см, 5 см и 20 см.
V = abc
VА = 30 • 20 • 25 = 600 • 25 = 15 000 (cм³)
VА = 15 • 5 • 20 = 15 • 100 = 1 500 (cм³)
V = VА— VВ = 15 000 — 1 500 = 13 500 (cм³)
Ответ: V= 13 500 cм³
631. Найдите объём фигуры, изображённой на рисунке 181 (размеры даны в сантиметрах).
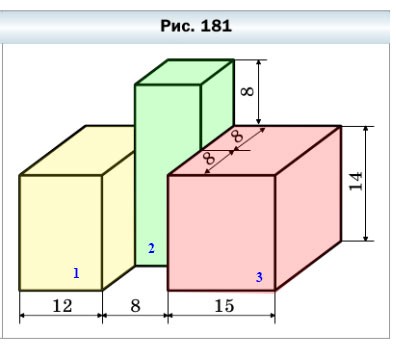
Фигуру, изображенную на рисунке 181, можно разделить на три прямоугольных параллелепипеда:

- жёлтый
- зелёный
- красный
Рассмотрим прямоугольный параллелепипед № 3 (красный):
- длина равна 15 см
- ширина равна 8 + 8 = 16 см
- высота равна 14 см
V = abc
V3 = 15 • 16 • 14 = 240 • 14 = 3 360 (cм³)
Рассмотрим прямоугольный параллелепипед № 2 (зелёный):
- длина равна 8 см
- ширина равна 8 см
- высота равна 14 + 8 = 22 см
V = abc
V2 = 8 • 8 • 22 = 64 • 22 = 1 408 (cм³)
Рассмотрим прямоугольный параллелепипед № 1 (жёлтый):
- длина равна 12 см
- ширина равна 8 + 8 = 16 см
- высота равна 14 см
V = abc
V1 = 12 • 16 • 14 = 192 • 14 = 2 688 (cм³)
Объем фигуры равен сумме объемов фигур, из которых она состоит.
V = V1 + V2 + V3= 2 688 + 1 408 + 3 360 = 7 456 (cм³)
Ответ: V = 7 456 cм³.
632. Ребро куба, изготовленного из цинка, равно 4 см. Найдите массу куба, если масса 1 см³ цинка составляет 7 г.
Дано:
a = 4 cм²
Масса 1 cм³ = 7 г
Масса куба = ? г
Решение:
V = a³
V = 4 • 4 • 4 = 16 • 4 = 64 (см³)
Масса 1 см³ куба равна 7 г, значит масса 64 см³ равна:
64 • 7 = 448 (г)
Ответ: 448 г.
633. Знайка сконструировал землеройную машину, которая за 8 ч может вырыть траншею, имеющую форму прямоугольного параллелепипеда, длиной 150 м, глубиной 80 см и шириной 60 см. Сколько кубометров земли выкапывает эта машина за 1 ч? Работу скольких коротышек выполняет эта машина, если за 8 ч один коротышка может выкопать 240 дм³ земли?

150 м = 15 000 см
1) 15 000 • 80 • 60 = 1 200 000 • 60 = 72 000 000 (см³) — объем выкопанной машиной траншеи.
72 000 000 см³ = 72 м³
2) 72 : 8 = 9 (м³) — выкапывает машина за 1 час.
72 м³ = 72 000 дм³
3) 72 000 : 240 = 300 (человек) — коротышек могут заменить 1 машину.
Ответ: 9 м³, 300 коротышек.
634. Куб и прямоугольный параллелепипед имеют равные объёмы. Найдите площадь поверхности куба, если длина прямоугольного параллелепипеда равна 12 см, что в 2 раза больше ширины и в 4 раза больше высоты параллелепипеда.

1) 12 • 2 = 6 (см) — сторона b прямоугольного параллелепипеда.
2) 12 • 4 = 3 (см) — сторона с прямоугольного параллелепипеда.
3) V = a • b • c = 12 • 6 • 3 = 72 • 3 = 216 (см³) — объём прямоугольного параллелепипеда.
V (прямоугольного параллелепипеда) = V (куба) = a³ = 216 (см³)
Значит сторона куба равна такому числу, которое при возведении в
