Какими свойствами обладает нормальное распределение результатов измерений
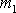
Нормальный закон распределения случайной величины
Значение для исследований в области ФКиС
Нормальное распределение случайной величины (гауссово распределение, распределение Гаусса, распределение Гаусса-Лапласа) – одно из непрерывных распределений, имеющее основопологающую роль в математической статистике. Причинами это являются:
- Многие эмпирические распределения можно успешно описать с помощью нормального закона распределения. Это чаще всего происходит в тех случаях, когда на показатель оказывает влияние большое число случайных факторов. При этом действие каждого фактора незначительно. Примерами показателей, которые распределяются по нормальному закону являются: рост, сила мышц, результаты в беге, прыжках, метаниях и др.
- Нормальное распределение обладает рядом благоприятных математических свойств, обеспечивших его широкое применение в статистике.
- Корректное использование критериев проверки статистических гипотез предполагает знание закона распределения экспериментальных данных. Так, например, использование t – критерия Стьюдента и F-критерия Фишера требует нормального распределения экспериментальных данных.
- Большинство экспериментальных распределений, полученных при исследованиях в области физической культуры и спорта может быть описано с помощью нормального распределения.
Однако в природе и в области ФКиС встречаются экспериментальные распределения, для описания которых модель нормального распределения малопригодна.
История изучения нормального распределения
Абрахам де Муавр (1667– 1754) – английский математик, предложил формулу нормального распределения, описывающую биномиальное распределение с вероятностью 0,5. Эта формула появилась в работе А.Муавра «Доктрина случайностей».
Карл Фридрих Гаусс (1777 – 1855) – немецкий математик, проводил исследования в области нормального распределения ошибок. Ввел это распределение как возникающее в результате многократных измерений движений небесных тел.
Пьер-Симон де Лаплас (1749-1827) — французский математик, механик, физик и астроном. П.-С. Лаплас обобщил результаты А. Муавра для произвольного биномиального распределения.
Адольф Кетле (1796-1874) – бельгийский математик, одним из первых применил нормальный закон распределения случайной величины к анализу биологических и социальных процессов.
Адольф Кетле изучал распределение солдат американской армии по росту. Он обратил внимание, что распределение роста подчиняется нормальному закону. Он писал: «…Человеческий рост, изменяющийся, по-видимому, самым случайным образом, тем не менее подчиняется самым точным законам, и эта особенность свойственна не только росту, она проявляется также в весе, силе, быстроте передвижений человека, во всех его физических … и нравственных способностях. Этот великий принцип… разнообразящий проявление человеческих способностей…кажется нам одним из самых удивительных законов мира» (А.Кетле, 1911).
Формула нормального распределения
Формула, описывающая нормальный закон распределения случайной величины, имеет следующий вид:
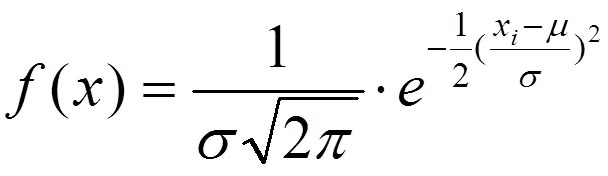
где: μ — генеральное среднее арифметическое; σ — генеральное стандартное отклонение.
Свойства нормального распределения
- Нормальная кривая имеет колокообразную форму, симметричную относительно точки x=µ, с точками перегиба, абсциссы которых отстоят от µ на ± σ.
- Нормальное распределение полностью определятся двумя параметрами: значением генерального среднего (µ) и генерального стандартного отклонения (σ).
- Медиана и мода нормального распределения совпадают и равны µ.
- Коэффициенты асимметрии и эксцесса нормального распределения равны нулю.
Нормированное отклонение
В области математической статистики важное место занимает нормированное отклонение (t) – показатель, представляющий отклонение той или иной варианты от средней величины, отнесенное к значению стандартного отклонения.Нормированное отклонение рассчитывает по формуле:
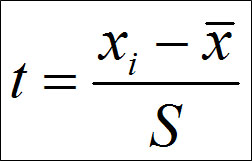
Нормированное отклонение позволяет установить, на сколько «сигм» отклоняются варианты от среднего значения. Например, необходимо определить насколько «сигм» отклоняется значение роста 180 см от среднего, если среднее арифметическое равно 170 см, а «сигма», то есть стандартное отклонение равно 10 см.
t= (180-170)/10 = 1.
Ответ: значение роста человека, равное 180 см отклоняется от среднего на одну «сигму».
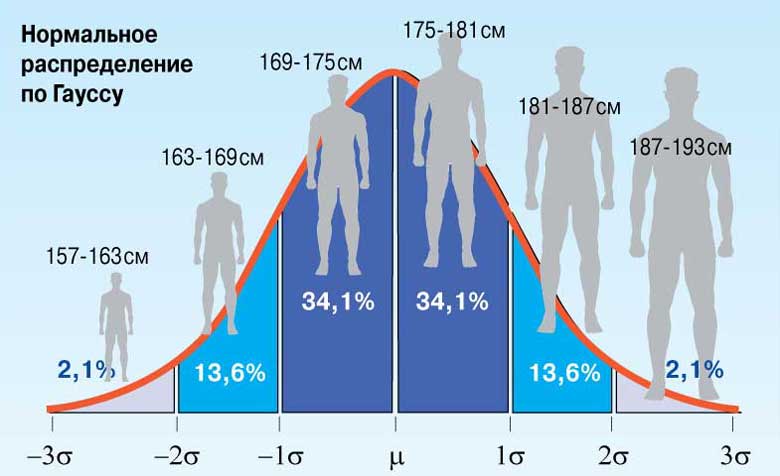
Рис.1. Нормированное нормальное распределение роста мужчин с параметрами: µ=0; σ = 1.
Для нормированного нормального распределения характерно, что в интервал µ± σ попадают 68 % всех результатов, в интервал µ± 2σ попадают 95% всех результатов, в интервал µ± 3σ попадают 99 % всех результатов.
В области физической культуры и спорта эти закономерности используют для разработки системы оценок. Так, В.М.Зациорским (рис. 2) предложено использовать следующую систему оценок результатов. То есть, если результат, показанный спортсменом, попал в интервал от -2σ до -1σ — он получает низкую оценку (Рассчитать, в какой интервал попадает результат можно при помощи нормированного отклонения. Это описано выше). Если результат попал в интервал от -1σ до -0,5σ — оценка ниже средней. Средний результат соответствует интервалу от -0,5σ до -0,5σ, результат, получивший оценку выше среднего — от 0,5 до 1σ. Высокий результат попадает в интервал от 1σ до 2σ.
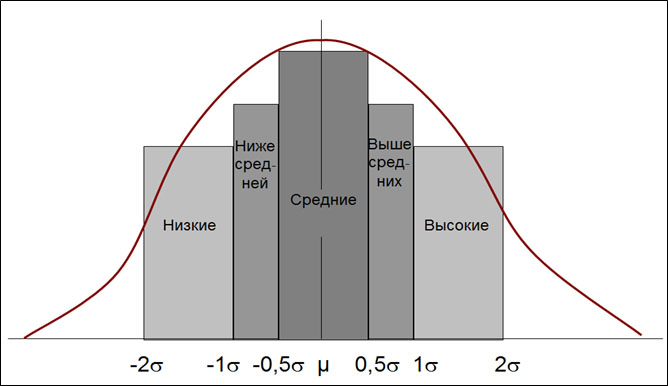
Рис.2
Критерии согласия
Чтобы проверить, соответствует ли распределение нормальному закону, существует много методов.
Можно использовать свойства нормального распределения (равенство среднего, моды и медианы).
Однако более точные результаты дают критерии согласия. В зависимости от объема выборки (n) следует использовать различные критерии:
- если объем выборки небольшой (n = 10) – критерий Шапиро – Уилки;
- если объем выборки более 40 — критерий хи-квадрат и критерий Колмогорова-Смирнова.
- в статистическом пакете Statgraphics Centurion существует специальная опция — критерии проверки нормальности распределения. В этой опции есть 4 критерия, посредством которых можно сделать вывод о соответствии эмпирического распределения нормальному закону.
Литература
- Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
- Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
- Кетле А. (1835) Социальная физика, или опыт исследования о развитии человеческих способностей. Т.1, 1911.- С. 38-39.
- Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.
Случайной
погрешностью измерения называется
составляющая погрешности, изменяющаяся
случайным образом (по знаку и значению)
при повторных измерениях одной и той
же физической величины, проведенных
с одинаковой тщательностью. Примеры
распределения случайных величин
Способы
нахождения значений случайной величины
зависят от вида функции ее распределения.
Однако на практике такие функции, как
правило, неизвестны. Если же случайный
характер результатов наблюдений
обусловлен погрешностями измерений,
то полагают, что наблюдения имеют
нормальное
распределение.
Это обусловлено тем, что погрешности
измерений складываются из большого
числа небольших возмущений, ни одно из
которых не является преобладающим.
Согласно же центральной
предельной теореме
сумма бесконечно большого числа взаимно
независимых бесконечно малых случайных
величин с любыми распределениями имеет
нормальное
распределение.
Нормальное распределение для
![]() случайной
случайной
величиных
с
математическим ожиданием
![]() и
и
дисперсиейs
имеет вид:
Реально даже воздействие
ограниченного числа возмущений приводит
к нормальному распределению результатов
измерений и их погрешностей. В
настоящее время наиболее полно разработан
математический аппарат именно для
случайных величин, имеющих нормальное
распределение. Если же предположение
о нормальности распределения отвергается,
то статистическая обработка наблюдений
существенно усложняется и в таком
случае невозможно рекомендовать общую
методику статистической обработки
наблюдений. Часто даже не известно,
какая характеристика распределения
может служить оценкой истинного значения
измеряемой величины.
Выше приведено
аналитическое выражение нормального
распределения для случайной измеряемой
величины х.
Переход к нормальному
распределению случайных погрешностей
![]() осуществляется
осуществляется
переносом центра распределений в![]() и
и
откладывания по оси абсцисс погрешности![]() .
.
Нормальное
распределение характеризуется двумя
парамет-рами: математическим ожиданием
m1
и
средним квадратическим отклонением
σ.
При многократных измерениях
несмещенной, состоятельной и эффективной
оценкой m1
для группы из n
наблюдений является среднее арифметическое
![]() :
:![]() .
.
Нужно
сказать, что среднее арифметическое
дает оценку математического ожидания
результата наблюдений и может бытьоценкой
истинного (действительного) значения
измеряемой
величины только после
исключения
систематических погрешностей.
Оценка
S
среднего квадратического отклонения
(СКО) дается
формулой:
![]() Эта
Эта
оценка характеризуетрассеяние
единичных результатов измерений в ряду
равноточных измерений одной и той же
величины около их среднего значения.
Другими оценками рассеяния результатов
в ряду измерений являются размах
(разница между наибольшим и наименьшим
значением), модуль средней
арифметической погрешности
(арифметическая сумма погрешностей,
деленная на число измерений) и
доверительная граница погрешности
(подробно рассматривается ниже).
СКО
является наиболее удобной характеристикой
погрешности в случае ее дальнейшего
преобразования. Например, для нескольких
некоррелированных слагаемых СКО суммы
определяется по
формуле:
![]() .
.
Оценка
S характеризует рассеяние единичных
результатов наблюдений относительно
среднего значения, то есть в случае,
если мы за результат измерений примем
отдельный исправленный результат
наблюдений. Если же в качестве результата
измерений принимается среднее
арифметическое, то СКО этого среднего![]() определяется
определяется
по формуле:![]() Нормальное
Нормальное
распределение погрешностей имеет
следующиесвойства:
симметричность,
т.е. погрешности, одинаковые по величине,
но противоположные по знаку,
встречаются одинаково часто;математическое
ожидание случайной погрешности равно
нулю;малые
погрешности более вероятны, чем большие;чем
меньше s, тем меньше рассеяние результатов
наблюдений и больше вероятность малых
погрешностей.
Доверительные
интервалы
Приведенные
выше оценки параметров распределения
случайных величин в виде среднего
арифметического для оценки математического
ожидания и СКО для оценки дисперсии
называются точечными
оценками,
так как они выражаются одним числом.
Однако в некоторых случаях знание
точечной оценки является недостаточным.
Наиболее корректной и наглядной оценкой
случайной погрешности измерений
является оценка с помощью доверительных
интервалов.
Симметричный интервал в границами
± Δх(Р)
называется доверительным
интервалом случайной
погрешности с довери-тельной вероятностью
Р,
если площадь кривой распределения
между абсциссами –Δх
и
+Δх
составляет Р-ю
часть всей площади под кривой плотности
распределения вероятностей. При
нормировке всей площади на единицу Р
представляет часть этой площади в долях
единицы (или в процентах). Другими
словами, в интервале от -Dх(Р)
до +Dх(Р)
с заданной вероятностью Р
встречаются Р×100%
всех возможных значений случайной
погрешности.
Доверительный интервал
для нормального распределения находится
по формуле:
![]() где
где
коэффициентt
зависит от доверительной вероятности
Р.
Для
нормального распределения существуют
следующие соотношения между доверительными
интервалами и доверительной вероятностью:
1s (Р=0,68), 2s (Р= 0,95), 3s (Р= 0,997), 4s (Р=0,999).
Доверительные
вероятности для выражения результатов
измерений и погрешностей в различных
областях науки и техники принимаются
равными. Так, в технических измерениях
принята доверительная вероятность
0,95. Лишь для особо точных и ответственных
измерений принимают более высокие
доверительные вероятности. В метрологии
используют, как правило, доверитель-ные
вероятности 0,97, в исключительных случаях
0,99. Необходимо отметить, что точность
измерений должна соответствовать
поставленной измерительной задаче.
Излишняя точность ведет к неоправданному
расходу средств. Недостаточная точность
измерений может привести к принятию
по его результатам ошибочных решений
с самыми непредсказуемыми последствиями,
вплоть до серьезных материальных потерь
или катастроф.
При
проведении многократных измерений
величины х,
подчиняющейся нормальному распределению,
доверительный интервал может быть
построен для любой доверительной
вероятности по формуле:
![]() гдеtq–
гдеtq–
коэффициент Стьюдента, зависящий от
числа наблюдений n
и выбранной доверительной вероятности
Р.
Он определяется с помощью таблицы
q-процентных
точек распределения Стьюдента, которая
имеет два параметра: k
= n
– 1 и q=
1 – P;
![]() –
–
оценка среднего квадратического
отклонения среднего арифметического.
Доверительный
интервал для погрешностиDх(Р)
позволяет построить доверительный
интервал для истинного (действительного)
значения измеряемой величины ,
оценкой которой является среднее
арифметическое
![]() .
.
Истинное значение измеряемой величины
находится с доверительной вероятностью
Р внутри интервала:![]() .
.
Доверительный интервал позволяет
выяснить, насколько может измениться
полученная в результате данной серии
измерений оценка измеряемой величины
при проведении повторной серии измерений
в тех же условиях. Необходимо отметить,
что доверительные интервалы строят
длянеслучайных
величин,
значения которых неизвестны. Такими
являются истинное значение измеряемой
величины и средние квадратические
отклонения. В то же время оценки этих
величин, получаемые в результате
обработки данных наблюдений, являются
случайными величинами.
Недостатком
доверительных интервалов при оценке
случай-ных погрешностей является то,
что при произвольно выбираемых
доверительных вероятностях нельзя
суммировать несколько погреш-ностей,
т.к. доверительный интервал суммы не
равен сумме довери-тельных интервалов.
Суммируются
дисперсии независимых случай-ных
величин:
Då
= åDi.
То есть, для возможности суммирования
составляющие случайной погрешности
должны быть представлены своими СКО,
а не предельными или доверительными
погрешностями.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.
Нормальное распределение в статистике
История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.
Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.
Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.
Кривая нормального распределения Гаусса имеет следующий вид.
График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.
На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.
Формула нормального распределения (плотности) следующая.
Формула состоит из двух математических констант:
π – число пи 3,142;
е – основание натурального логарифма 2,718;
двух изменяемых параметров, которые задают форму конкретной кривой:
m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);
σ2 – дисперсия;
ну и сама переменная x, для которой высчитывается плотность вероятности.
Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ2). Кратко обозначается N(m, σ2) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ2 характеризует размах вариации, то есть «размазанность» данных.
Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.
А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.
Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.
Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:
Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как
P(a ≤ X < b) = Ф(b) – Ф(a)
Стандартное нормальное распределение
Нормальное распределение зависит от параметров средней и дисперсии, из-за чего плохо видны его свойства. Хорошо бы иметь некоторый эталон распределения, не зависящий от масштаба данных. И он существует. Называется стандартным нормальным распределением. На самом деле это обычное нормальное нормальное распределение, только с параметрами математического ожидания 0, а дисперсией – 1, кратко записывается N(0, 1).
Любое нормальное распределение легко превращается в стандартное путем нормирования:
где z – новая переменная, которая используется вместо x;
m – математическое ожидание;
σ – стандартное отклонение.
Для выборочных данных берутся оценки:
Среднее арифметическое и дисперсия новой переменной z теперь также равны 0 и 1 соответственно. В этом легко убедиться с помощью элементарных алгебраических преобразований.
В литературе встречается название z-оценка. Это оно самое – нормированные данные. Z-оценку можно напрямую сравнивать с теоретическими вероятностями, т.к. ее масштаб совпадает с эталоном.
Посмотрим теперь, как выглядит плотность стандартного нормального распределения (для z-оценок). Напомню, что функция Гаусса имеет вид:
Подставим вместо (x-m)/σ букву z, а вместо σ – единицу, получим функцию плотности стандартного нормального распределения:
График плотности:
Центр, как и ожидалось, находится в точке 0. В этой же точке функция Гаусса достигает своего максимума, что соответствует принятию случайной величиной своего среднего значения (т.е. x-m=0). Плотность в этой точке равна 0,3989, что можно посчитать даже в уме, т.к. e0=1 и остается рассчитать только соотношение 1 на корень из 2 пи.
Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.
Функция стандартного нормального распределения позволяет рассчитывать вероятности.
Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.
Таблица нормального распределения
Таблицы нормального распределения встречаются двух типов:
— таблица плотности;
— таблица функции (интеграла от плотности).
Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.
В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец , т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).
Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.
Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.
На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.
В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:
Это факт показан на картинке:
Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.
Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:
Для наглядности можно взглянуть на рисунок.
На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.
Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:
Рисунок ниже.
Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.
Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.
Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:
Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.
Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.
Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.
То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.
Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).
Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).
Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.
Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.
Так выглядит правило 3 сигм для нормального распределения на диаграмме.
С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.
Нормальное распределение в Excel
В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.
Функция НОРМ.СТ.РАСП
Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ(z) или вероятности Φ(z) по нормированным данным (z).
=НОРМ.СТ.РАСП(z;интегральная)
z – значение стандартизованной переменной
интегральная – если 0, то рассчитывается плотность ϕ(z), если 1 – значение функции Ф(z), т.е. вероятность P(Z<z).
Рассчитаем плотность и значение функции для различных z: -3, -2, -1, 0, 1, 2, 3 (их укажем в ячейке А2).
Для расчета плотности потребуется формула =НОРМ.СТ.РАСП(A2;0). На диаграмме ниже – это красная точка.
Для расчета значения функции =НОРМ.СТ.РАСП(A2;1). На диаграмме – закрашенная площадь под нормальной кривой.
В реальности чаще приходится рассчитывать вероятность того, что случайная величина не выйдет за некоторые пределы от средней (в среднеквадратичных отклонениях, соответствующих переменной z), т.е. P(|Z|<z).
Определим, чему равна вероятность попадания случайной величины в пределы ±1z, ±2z и ±3z от нуля. Потребуется формула 2Ф(z)-1, в Excel =2*НОРМ.СТ.РАСП(A2;1)-1.
На диаграмме отлично видны основные основные свойства нормального распределения, включая правило трех сигм. Функция НОРМ.СТ.РАСП – это автоматическая таблица значений функции нормального распределения в Excel.
Может стоять и обратная задача: по имеющейся вероятности P(Z<z) найти стандартизованную величину z ,то есть квантиль стандартного нормального распределения.
Функция НОРМ.СТ.ОБР
НОРМ.СТ.ОБР рассчитывает обратное значение функции стандартного нормального распределения. Синтаксис состоит из одного параметра:
=НОРМ.СТ.ОБР(вероятность)
вероятность – это вероятность.
Данная формула используется так же часто, как и предыдущая, ведь по тем же таблицам искать приходится не только вероятности, но и квантили.
Например, при расчете доверительных интервалов задается доверительная вероятность, по которой нужно рассчитать величину z.
Учитывая то, что доверительный интервал состоит из верхней и нижней границы и то, что нормальное распределение симметрично относительно нуля, достаточно получить верхнюю границу (положительное отклонение). Нижняя граница берется с отрицательным знаком. Обозначим доверительную вероятность как γ (гамма), тогда верхняя граница доверительного интервала рассчитывается по следующей формуле.
Рассчитаем в Excel значения z (что соответствует отклонению от средней в сигмах) для нескольких вероятностей, включая те, которые наизусть знает любой статистик: 90%, 95% и 99%. В ячейке B2 укажем формулу: =НОРМ.СТ.ОБР((1+A2)/2). Меняя значение переменной (вероятности в ячейке А2) получим различные границы интервалов.
Доверительный интервал для 95% равен 1,96, то есть почти 2 среднеквадратичных отклонения. Отсюда легко даже в уме оценить возможный разброс нормальной случайной величины. В общем, доверительным вероятностям 90%, 95% и 99% соответствуют доверительные интервалы ±1,64, ±1,96 и ±2,58 σ.
В целом функции НОРМ.СТ.РАСП и НОРМ.СТ.ОБР позволяют произвести любой расчет, связанный с нормальным распределением. Но, чтобы облегчить и уменьшить количество действий, в Excel есть несколько других функций. Например, для расчета доверительных интервалов средней можно использовать ДОВЕРИТ.НОРМ. Для проверки статистической гипотезы о средней арифметической есть формула Z.ТЕСТ.
Рассмотрим еще пару полезных формул с примерами.
Функция НОРМ.РАСП
Функция НОРМ.РАСП отличается от НОРМ.СТ.РАСП лишь тем, что ее используют для обработки данных любого масштаба, а не только нормированных. Параметры нормального распределения указываются в синтаксисе.
=НОРМ.РАСП(x;среднее;стандартное_откл;интегральная)
x – значение (или ссылка на ячейку), для которого рассчитывается плотность или значение функции нормального распределения
среднее – математическое ожидание, используемое в качестве первого параметра модели нормального распределения
стандартное_откл – среднеквадратичное отклонение – второй параметр модели
интегральная – если 0, то рассчитывается плотность, если 1 – то значение функции, т.е. P(X<x).
Например, плотность для значения 15, которое извлекли из нормальной выборки с матожиданием 10, стандартным отклонением 3, рассчитывается так:
Если последний параметр поставить 1, то получим вероятность того, что нормальная случайная величина окажется меньше 15 при заданных параметрах распределения. Таким образом, вероятности можно рассчитывать напрямую по исходным данным.
Функция НОРМ.ОБР
Это квантиль нормального распределения, т.е. значение обратной функции. Синтаксис следующий.
=НОРМ.ОБР(вероятность;среднее;стандартное_откл)
вероятность – вероятность
среднее – матожидание
стандартное_откл – среднеквадратичное отклонение
Назначение то же, что и у НОРМ.СТ.ОБР, только функция работает с данными любого масштаба.
Пример показан в ролике в конце статьи.
Моделирование нормального распределения
Для некоторых задач требуется генерация нормальных случайных чисел. Готовой функции для этого нет. Однако В Excel есть две функции, которые возвращают случайные числа: СЛУЧМЕЖДУ и СЛЧИС. Первая выдает случайные равномерно распределенные целые числа в указанных пределах. Вторая функция генерирует равномерно распределенные случайные числа между 0 и 1. Чтобы сделать искусственную выборку с любым заданным распределением, нужна функция СЛЧИС.
Допустим, для проведения эксперимента необходимо получить выборку из нормально распределенной генеральной совокупности с матожиданием 10 и стандартным отклонением 3. Для одного случайного значения напишем формулу в Excel.
=НОРМ.ОБР(СЛЧИС();10;3)
Протянем ее на необходимое количество ячеек и нормальная выборка готова.
Для моделирования стандартизованных данных следует воспользоваться НОРМ.СТ.ОБР.
Процесс преобразования равномерных чисел в нормальные можно показать на следующей диаграмме. От равномерных вероятностей, которые генерируются формулой СЛЧИС, проведены горизонтальные линии до графика функции нормального распределения. Затем от точек пересечения вероятностей с графиком опущ?
