Какими свойствами обладает квадрат

Квадрат, его свойства и признаки.
Определение. Квадратом называется прямоугольник, у которого все стороны равны.

Для квадрата можно ввести несколько определений. Самое ёмкое мы уже привели. Но можно определить квадрат следующим образом:
Квадратом называется четырёхугольник, у которого все стороны равны, а углы прямые.
Квадратом называется параллелограмм, у которого все стороны и углы равны.
Квадратом называется ромб, у которого все углы прямые.
Поскольку квадрат является и параллелограммом, и прямоугольником, и ромбом, то он обладает теми же свойствами, что и все перечисленные четырёхугольники.
У квадрата диагонали пересекаются и точкой пересечения делятся пополам.
У квадрата диагонали взаимно перпендикулярны.
У квадрата диагонали являются биссектрисами его углов.
У квадрата диагонали равны.
У квадрата стороны являются высотами.
Каждая диагональ квадрата делит его на равные прямоугольные треугольники.
Теперь определим признаки квадрата.
ТЕОРЕМА (I признак). Если в прямоугольнике две его смежные стороны равны, то он является квадратом.

Дано: – прямоугольник
Доказать: – квадрат.
Доказательство.
Так как – прямоугольник, то у него противолежащие стороны равны.
– квадрат (по определению), ч.т.д.
ТЕОРЕМА (II признак). Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.
Дано: – прямоугольник
Доказать: – квадрат.
Доказательство.
Рассмотрим .
по свойству диагоналей прямоугольника, значит, – медиана (по опред-нию).
– высота , т.к. . Значит, в является и медианой и высотой, поэтому этот треугольник является равнобедренным (по признаку равнобедренного треугольника), т.е. . Согласно I признаку квадрата, прямоугольник является квадратом, ч.т.д.
ТЕОРЕМА (III признак). Если в прямоугольнике одна из диагоналей является биссектрисой его угла, то такой прямоугольник является квадратом.

Дано: – прямоугольник
– диагональ
– биссектриса
Доказать: – квадрат.
Доказательство.
Так как – биссектриса , то .
по свойству внутренних накрест лежащих углов при параллельных прямых. Значит, , следовательно – равнобедренный, и . По I признаку квадрата, прямоугольник является квадратом, ч.т.д.
ТЕОРЕМА (IV признак). Если в ромбе диагонали равны, то этот ромб является квадратом.
Дано: – ромб
— диагонали
Доказать: – квадрат.
Доказательство.
Рассмотрим и .
по III признаку равенства треугольников. Значит, все соответствующие углы у этих треугольников равны, т.е. . Эти углы являются внутренними односторонними при параллельных прямых и , следовательно, их сумма равна , т.е. , а, значит, и . Так как в ромбе противолежащие углы равны, то и все остальные углы также равны по . Значит, такой ромб является квадратом, ч.т.д.
ТЕОРЕМА (V признак). Если в параллелограмме диагонали перпендикулярны и равны, то такой параллелограмм является квадратом.
Дано: – параллелограмм
Доказать: – квадрат.
Доказательство.
Так как , то по II признаку ромба, параллелограмм является ромбом.
Так как , то по IV признаку квадрата, ромб является квадратом, ч.т.д.
ТЕОРЕМА (VI признак). Если в четырёхугольнике диагонали равны, взаимно перпендикулярны и точкой пересечения делятся пополам, то такой четырёхугольник является квадратом.
Дано: – четырёхугольник
Доказать: – квадрат.
Доказательство.
1. Так как , то четырёхугольник является параллелограммом (по признаку параллелограмма).
2. Так как , то параллелограмм является квадратом (по V признаку квадрата), ч.т.д.
ТЕОРЕМА (VII признак). Если в четырёхугольнике все стороны равны и среди внутренних углов есть один прямой угол, то такой четырёхугольник является квадратом.
Дано: – четырёхугольник
Доказать: – квадрат.
Доказательство.
1. Так как , то четырёхугольник является ромбом (по V признаку ромба).
2. Так как , то ромб, который по определению является параллелограммом, является прямоугольником (по III признаку прямоугольника), значит, все углы в этом четырёхугольнике прямые.
3. Итак, прямоугольник , у которого все стороны равны, является квадратом (по определению), ч.т.д.
Итак, признаки квадрата:
Если в прямоугольнике две его смежные стороны равны, то он является квадратом.
Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.
Если в прямоугольнике одна из диагоналей является биссектрисой его угла, то такой прямоугольник является квадратом.
Если в ромбе диагонали равны, то этот ромб является квадратом.
Если в параллелограмме диагонали перпендикулярны и равны, то такой параллелограмм является квадратом.
Если в четырёхугольнике диагонали равны, взаимно перпендикулярны и точкой пересечения делятся пополам, то такой четырёхугольник является квадратом.
Если в четырёхугольнике все стороны равны и среди внутренних углов есть один прямой угол, то такой четырёхугольник является квадратом.
Периметр квадрата равен см. Найдите сторону квадрата .
На рисунке четырёхугольник – квадрат, . Докажите, что выпуклый четырёхугольник также является квадратом.

На рисунке четырёхугольник – прямоугольник, . Докажите, что выпуклый четырёхугольник является квадратом.

В треугольнике . На сторонах и взяты точки и , а на стороне – точки и так, что четырёхугольник является квадратом, . Найдите .
В треугольнике . На сторонах отмечены точки соответственно так, что четырёхугольник является квадратом, . Найдите .
На сторонах и квадрата отмечены точки и соответственно, . Отрезки и пересекаются в точке . Найдите .
На сторонах квадрата отмечены соответственно точки . Сравните отрезки и .
На катетах и прямоугольного треугольника построены квадраты и . Докажите, что сумма расстояний от точек и до прямой равна .
На катетах и прямоугольного треугольника построены квадраты и . Прямые и пересекаются в точке . Докажите, что .
Длина проекции одной из сторон квадрата на его диагональ равна . Найдите длину диагонали.
В четырёхугольнике диагонали взаимно перпендикулярны. Докажите, что отрезки, соединяющие середины противоположных сторон, равны.

Дан квадрат . Докажите, что – квадрат.
Дан квадрат . Докажите, что – ромб.

Дан квадрат . На стороне взята точка такая, что . Докажите, что точки – вершины равнобедренного треугольника.
Дан квадрат . Точки – середины его сторон соответственно. Докажите, что .
Дан квадрат . Точки и делят его стороны и так, что . Докажите, что .
Квадраты и имеют общую вершину . Докажите, что медиана треугольника перпендикулярна отрезку .

Внутри квадрата взята точка так, что . Докажите, что треугольник равносторонний.
На рисунке – квадрат, точка принадлежит , точка принадлежит , точка принадлежит , прямые и пересекаются в точке . Докажите, что .

В равнобедренный прямоугольный треугольник, каждый катет которого равен см, вписан квадрат, имеющий с ним один общий угол. Найдите периметр квадрата.
В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины находятся на гипотенузе, а две другие – на катетах. Определите сторону квадрата, если известно, что гипотенуза равна 30 дм.
В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Определите стороны этого прямоугольника, зная, что одна из них втрое больше другой и что диагональ квадрата равна дм.
В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Определите стороны этого прямоугольника, зная, что одна из них вдвое больше другой и что диагональ квадрата равна см.
Точка расположена во внутренней области квадрата так, что расстояния от неё до сторон и пропорциональны соответственно числам и , а расстояние от до прямой равно см. Найдите периметр этого квадрата.
Точка расположена во внутренней области квадрата так, что расстояния от неё до сторон и пропорциональны соответственно числам и , а расстояние от до прямой равно м. Найдите периметр этого квадрата.
Точка лежит на стороне квадрата . Высоты треугольников и , проведённые из точки , равны соответственно и . Найдите произведение длин диагоналей этого квадрата.

Точка расположена во внутренней области квадрата так, что расстояния от неё до сторон и пропорциональны соответственно числам и , а расстояние от до прямой равно м. Найдите периметр этого квадрата.
Точка лежит на стороне квадрата . Высоты треугольников и , проведённые из точки , равны соответственно и . Найдите произведение длин диагоналей этого квадрата.

На сторонах и квадрата отмечены точки и соответственно так, что . Определите взаимное расположение прямых и .
В равнобедренный прямоугольный треугольник вписан квадрат , имеющий с ним общий угол . Найдите периметр квадрата, если катет треугольника равен см.

Внутри квадрата отмечена такая точка , что треугольник равносторонний. Найдите угол .

В равнобедренный прямоугольный треугольник вписан квадрат , имеющий с ним общий прямой угол. Найдите катет треугольника, если периметр квадрата равен см.

Внутри квадрата отмечена такая точка , что треугольник равносторонний. Найдите угол .

Через вершины квадрата проведены прямые, параллельные его диагоналям. Определите вид образованного ими четырёхугольника и вычислите его периметр, если диагональ квадрата равна см.
Через точку – точку пересечения диагоналей квадрата проведена прямая, параллельная стороне и пересекающая стороны и в точках и соответственно. Найдите периметр квадрата, если известно, что .
Найдите периметр квадрата по данным на рисунке.

7
Êâàäðàò — ïðàâèëüíûé ÷åòûð¸õóãîëüíèê. Ó êâàäðàòà âñå óãëû è ñòîðîíû îäèíàêîâû.
Êâàäðàòû ðàçëè÷àþòñÿ ëèøü äëèíîé ñòîðîíû, à âñå 4 óãëà ïðÿìûå è ðàâíû 90°.
Êâàäðàòîì ìîæåò ñòàòü ïàðàëëåëîãðàìì, ðîìá ëèáî ïðÿìîóãîëüíèê, êîãäà ó íèõ îäèíàêîâûå äëèíû äèàãîíàëåé, ñòîðîí è ðàâíûå óãëû.


Ñâîéñòâà êâàäðàòà.
— ó âñåõ 4-õ ñòîðîí êâàäðàòà îäèíàêîâàÿ äëèíà, ò.å. ñòîðîíû êâàäðàòà ðàâíû:
AB = BC = CD = AD
— ïðîòèâîëåæàùèå ñòîðîíû êâàäðàòà ïàðàëëåëüíû:
AB||CD, BC||AD
— êàæäûé óãîë êâàäðàòà ïðÿìîé:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
— ñóììà óãëîâ êâàäðàòà ðàâíà 360°:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
— êàæäàÿ äèàãîíàëü êâàäðàòà èìååò òàêóþ æå äëèíó, êàê è äðóãàÿ:
AC = BD
— êàæäàÿ èç äèàãîíàëåé êâàäðàòà äåëèò êâàäðàò íà 2 îäèíàêîâûå ñèììåòðè÷íûå ôèãóðû.
— óãîë ïåðåñå÷åíèÿ äèàãîíàëåé êâàäðàòà ðàâåí 90°, ïåðåñåêàÿ äðóã äðóãà, äèàãîíàëè äåëÿòñÿ íà äâå ðàâíûå ÷àñòè:
AC┴BD;AO = BO = CO = DO = d/2
— òî÷êó ïåðåñå÷åíèÿ äèàãîíàëåé íàçûâàþò öåíòð êâàäðàòà è îíà îêàçûâàåòñÿ öåíòðîì âïèñàííîé è îïèñàííîé îêðóæíîñòåé.
— âñå äèàãîíàëè äåëÿò óãîë êâàäðàòà íà äâå ðàâíûå ÷àñòè, òàêèì îáðàçîì, îíè îêàçûâàþòñÿ áèññåêòðèñàìè óãëîâ êâàäðàòà:
ΔABC = ΔADC = ΔBAD = ΔBCD
∠ACB = ∠ACD = ∠BDC = ∠BDA = ∠CAB = ∠CAD = ∠DBC = ∠DBA = 45°
— äèàãîíàëè äåëÿò êâàäðàò íà 4 îäèíàêîâûõ òðåóãîëüíèêà, êðîìå òîãî, ïîëó÷åííûå òðåóãîëüíèêè â îäíî âðåìÿ è ðàâíîáåäðåííûå è ïðÿìîóãîëüíûå:
ΔAOB = ΔBOC = ΔCOD = ΔDOA
Äèàãîíàëü êâàäðàòà.
Äèàãîíàëüþ êâàäðàòà ÿâëÿåòñÿ âñÿêèé îòðåçîê, êîòîðûé ñîåäèíÿåò 2-å âåðøèíû ïðîòèâîëåæàùèõ óãëîâ êâàäðàòà.
Äèàãîíàëü âñÿêîãî êâàäðàòà áîëüøå ñòîðîíû ýòîãî êâàäðàòà â √2 ðàç.
Ôîðìóëû äëÿ îïðåäåëåíèÿ äëèíû äèàãîíàëè êâàäðàòà:
1. Ôîðìóëà äèàãîíàëè êâàäðàòà ÷åðåç ñòîðîíó êâàäðàòà:

2. Ôîðìóëà äèàãîíàëè êâàäðàòà ÷åðåç ïëîùàäü êâàäðàòà:

3. Ôîðìóëà äèàãîíàëè êâàäðàòà ÷åðåç ïåðèìåòð êâàäðàòà:

4. Ñóììà óãëîâ êâàäðàòà = 360°:

5. Äèàãîíàëè êâàäðàòà îäíîé äëèíû:

6. Âñå äèàãîíàëè êâàäðàòà äåëÿò êâàäðàò íà 2-å îäèíàêîâûå ôèãóðû, êîòîðûå ñèììåòðè÷íû:

7. Óãîë ïåðåñå÷åíèÿ äèàãîíàëåé êâàäðàòà ðàâåí 90°, ïåðåñåêàÿ äðóã äðóãà, äèàãîíàëè äåëÿòñÿ íà äâå ðàâíûå ÷àñòè:

8. Ôîðìóëà äèàãîíàëè êâàäðàòà ÷åðåç äëèíó îòðåçêà l:

9. Ôîðìóëà äèàãîíàëè êâàäðàòà ÷åðåç ðàäèóñ âïèñàííîé îêðóæíîñòè:

R — ðàäèóñ âïèñàííîé îêðóæíîñòè;
D — äèàìåòð âïèñàííîé îêðóæíîñòè;
d — äèàãîíàëü êâàäðàòà.

10. Ôîðìóëà äèàãîíàëè êâàäðàòà ÷åðåç ðàäèóñ îïèñàííîé îêðóæíîñòè:

R – ðàäèóñ îïèñàííîé îêðóæíîñòè;
D – äèàìåòð îïèñàííîé îêðóæíîñòè;
d – äèàãîíàëü.

11. Ôîðìóëà äèàãîíàëè êâàäðàòà ÷åðåç ëèíèþ, êîòîðàÿ âûõîäèò èç óãëà íà ñåðåäèíó ñòîðîíû êâàäðàòà:

C – ëèíèÿ, êîòîðàÿ âûõîäèò èç óãëà íà ñåðåäèíó ñòîðîíû êâàäðàòà;
d – äèàãîíàëü.

Ïåðèìåòð êâàäðàòà. Ïëîùàäü êâàäðàòà.
Âïèñàííûé êðóã â êâàäðàò – ýòî êðóã, ïðèìûêàþùèé ê ñåðåäèíàì ñòîðîí êâàäðàòà è èìåþùèé öåíòð íà ïåðåñå÷åíèè äèàãîíàëåé êâàäðàòà.
Ðàäèóñ âïèñàííîé îêðóæíîñòè — ñòîðîíà êâàäðàòà (ïîëîâèíà).
Ïëîùàäü êðóãà âïèñàííîãî â êâàäðàò ìåíüøå ïëîùàäè êâàäðàòà â π/4 ðàçà.
Êðóã, îïèñàííûé âîêðóã êâàäðàòà — ýòî êðóã, êîòîðûé ïðîõîäèò ÷åðåç 4-ðå âåðøèíû êâàäðàòà è êîòîðûé èìååò öåíòð íà ïåðåñå÷åíèè äèàãîíàëåé êâàäðàòà.
Ðàäèóñ îêðóæíîñòè îïèñàííîé âîêðóã êâàäðàòà áîëüøå ðàäèóñà âïèñàííîé îêðóæíîñòè â √2 ðàç.
Ðàäèóñ îêðóæíîñòè îïèñàííîé âîêðóã êâàäðàòà ðàâåí 1/2 äèàãîíàëè.
Ïëîùàäü êðóãà îïèñàííîãî âîêðóã êâàäðàòà áîëüøàÿ ïëîùàäü òîãî æå êâàäðàòà â π/2 ðàç.
Êâàäðàò — ïðàâèëüíûé ÷åòûð¸õóãîëüíèê. Ó êâàäðàòà âñå óãëû è ñòîðîíû îäèíàêîâû.
Êâàäðàòû ðàçëè÷àþòñÿ ëèøü äëèíîé ñòîðîíû, à âñå 4 óãëà ïðÿìûå è ðàâíû 90°.
Êâàäðàòîì ìîæåò ñòàòü ïàðàëëåëîãðàìì, ðîìá ëèáî ïðÿìîóãîëüíèê, êîãäà ó íèõ îäèíàêîâûå äëèíû äèàãîíàëåé, ñòîðîí è ðàâíûå óãëû.


Ñâîéñòâà êâàäðàòà.
— ó âñåõ 4-õ ñòîðîí êâàäðàòà îäèíàêîâàÿ äëèíà, ò.å. ñòîðîíû êâàäðàòà ðàâíû:
AB = BC = CD = AD
— ïðîòèâîëåæàùèå ñòîðîíû êâàäðàòà ïàðàëëåëüíû:
AB||CD, BC||AD
— êàæäûé óãîë êâàäðàòà ïðÿìîé:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
— ñóììà óãëîâ êâàäðàòà ðàâíà 360°:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
— êàæäàÿ äèàãîíàëü êâàäðàòà èìååò òàêóþ æå äëèíó, êàê è äðóãàÿ:
AC = BD
— êàæäàÿ èç äèàãîíàëåé êâàäðàòà äåëèò êâàäðàò íà 2 îäèíàêîâûå ñèììåòðè÷íûå ôèãóðû.
— óãîë ïåðåñå÷åíèÿ äèàãîíàëåé êâàäðàòà ðàâåí 90°, ïåðåñåêàÿ äðóã äðóãà, äèàãîíàëè äåëÿòñÿ íà äâå ðàâíûå ÷àñòè:
AC┴BD;AO = BO = CO = DO = d/2
— òî÷êó ïåðåñå÷åíèÿ äèàãîíàëåé íàçûâàþò öåíòð êâàäðàòà è îíà îêàçûâàåòñÿ öåíòðîì âïèñàííîé è îïèñàííîé îêðóæíîñòåé.
— âñå äèàãîíàëè äåëÿò óãîë êâàäðàòà íà äâå ðàâíûå ÷àñòè, òàêèì îáðàçîì, îíè îêàçûâàþòñÿ áèññåêòðèñàìè óãëîâ êâàäðàòà:
ΔABC = ΔADC = ΔBAD = ΔBCD
∠ACB = ∠ACD = ∠BDC = ∠BDA = ∠CAB = ∠CAD = ∠DBC = ∠DBA = 45°
— äèàãîíàëè äåëÿò êâàäðàò íà 4 îäèíàêîâûõ òðåóãîëüíèêà, êðîìå òîãî, ïîëó÷åííûå òðåóãîëüíèêè â îäíî âðåìÿ è ðàâíîáåäðåííûå è ïðÿìîóãîëüíûå:
ΔAOB = ΔBOC = ΔCOD = ΔDOA
Äèàãîíàëü êâàäðàòà.
Äèàãîíàëüþ êâàäðàòà ÿâëÿåòñÿ âñÿêèé îòðåçîê, êîòîðûé ñîåäèíÿåò 2-å âåðøèíû ïðîòèâîëåæàùèõ óãëîâ êâàäðàòà.
Äèàãîíàëü âñÿêîãî êâàäðàòà áîëüøå ñòîðîíû ýòîãî êâàäðàòà â √2 ðàç.
Ôîðìóëû äëÿ îïðåäåëåíèÿ äëèíû äèàãîíàëè êâàäðàòà:
1. Ôîðìóëà äèàãîíàëè êâàäðàòà ÷åðåç ñòîðîíó êâàäðàòà:

2. Ôîðìóëà äèàãîíàëè êâàäðàòà ÷åðåç ïëîùàäü êâàäðàòà:

3. Ôîðìóëà äèàãîíàëè êâàäðàòà ÷åðåç ïåðèìåòð êâàäðàòà:

4. Ñóììà óãëîâ êâàäðàòà = 360°:

5. Äèàãîíàëè êâàäðàòà îäíîé äëèíû:

6. Âñå äèàãîíàëè êâàäðàòà äåëÿò êâàäðàò íà 2-å îäèíàêîâûå ôèãóðû, êîòîðûå ñèììåòðè÷íû:

7. Óãîë ïåðåñå÷åíèÿ äèàãîíàëåé êâàäðàòà ðàâåí 90°, ïåðåñåêàÿ äðóã äðóãà, äèàãîíàëè äåëÿòñÿ íà äâå ðàâíûå ÷àñòè:

8. Ôîðìóëà äèàãîíàëè êâàäðàòà ÷åðåç äëèíó îòðåçêà l:

9. Ôîðìóëà äèàãîíàëè êâàäðàòà ÷åðåç ðàäèóñ âïèñàííîé îêðóæíîñòè:

R — ðàäèóñ âïèñàííîé îêðóæíîñòè;
D — äèàìåòð âïèñàííîé îêðóæíîñòè;
d — äèàãîíàëü êâàäðàòà.

10. Ôîðìóëà äèàãîíàëè êâàäðàòà ÷åðåç ðàäèóñ îïèñàííîé îêðóæíîñòè:

R – ðàäèóñ îïèñàííîé îêðóæíîñòè;
D – äèàìåòð îïèñàííîé îêðóæíîñòè;
d – äèàãîíàëü.

11. Ôîðìóëà äèàãîíàëè êâàäðàòà ÷åðåç ëèíèþ, êîòîðàÿ âûõîäèò èç óãëà íà ñåðåäèíó ñòîðîíû êâàäðàòà:

C – ëèíèÿ, êîòîðàÿ âûõîäèò èç óãëà íà ñåðåäèíó ñòîðîíû êâàäðàòà;
d – äèàãîíàëü.

Ïåðèìåòð êâàäðàòà. Ïëîùàäü êâàäðàòà.
Âïèñàííûé êðóã â êâàäðàò – ýòî êðóã, ïðèìûêàþùèé ê ñåðåäèíàì ñòîðîí êâàäðàòà è èìåþùèé öåíòð íà ïåðåñå÷åíèè äèàãîíàëåé êâàäðàòà.
Ðàäèóñ âïèñàííîé îêðóæíîñòè — ñòîðîíà êâàäðàòà (ïîëîâèíà).
Ïëîùàäü êðóãà âïèñàííîãî â êâàäðàò ìåíüøå ïëîùàäè êâàäðàòà â π/4 ðàçà.
Êðóã, îïèñàííûé âîêðóã êâàäðàòà — ýòî êðóã, êîòîðûé ïðîõîäèò ÷åðåç 4-ðå âåðøèíû êâàäðàòà è êîòîðûé èìååò öåíòð íà ïåðåñå÷åíèè äèàãîíàëåé êâàäðàòà.
Ðàäèóñ îêðóæíîñòè îïèñàííîé âîêðóã êâàäðàòà áîëüøå ðàäèóñà âïèñàííîé îêðóæíîñòè â √2 ðàç.
Ðàäèóñ îêðóæíîñòè îïèñàííîé âîêðóã êâàäðàòà ðàâåí 1/2 äèàãîíàëè.
Ïëîùàäü êðóãà îïèñàííîãî âîêðóã êâàäðàòà áîëüøàÿ ïëîùàäü òîãî æå êâàäðàòà â π/2 ðàç.
Автор:
02 апреля 2019 08:28
Мы все учили в школе геометрию, но с годами многое подзабыли. Чтобы не попасть впросак, когда ваш ребенок спросит, чем ромб отличается от квадрата, почитайте эту статью и вспомните, казалось бы, давно забытое.

Источник:
Очень часто четкое определение какого-либо предмета дает о нем практически полную информацию. Вот, например, ромб и квадрат – едва ли не самые распространенные геометрические фигуры. Глядя на них, мы понимаем, что они отличаются, но вот чем и как это объяснить простыми словами? Давайте разбираться.
Что представляет собой ромб
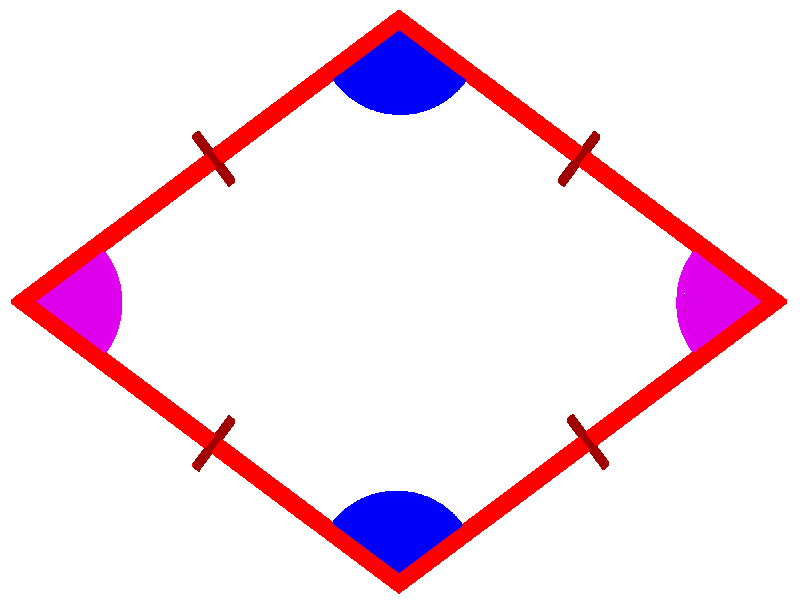
Источник:
Геометрия дает такое определение ромба: «Ромбом называется параллелограмм…». Стоп, сначала придется вспомнить, что такое параллелограмм. Это многоугольник с четырьмя углами, у которого противоположные стороны параллельны. А какими же свойствами обладает ромб как разновидность параллелограмма? Вот они:
1. Если соединить противоположные углы ромба диагоналями, то углы их пересечения составят 90º, то есть они взаимно перпендикулярны.
2. Эти диагонали (вообще-то в строгой науке геометрии принято говорить «отрезки диагоналей ромба») лежат на биссектрисах, делящих его углы пополам (помните школьный стишок: «Биссектриса – это такая крыса, которая бегает по углам и делит угол пополам»? Ребенку тоже будет полезно).
Что представляет собой квадрат
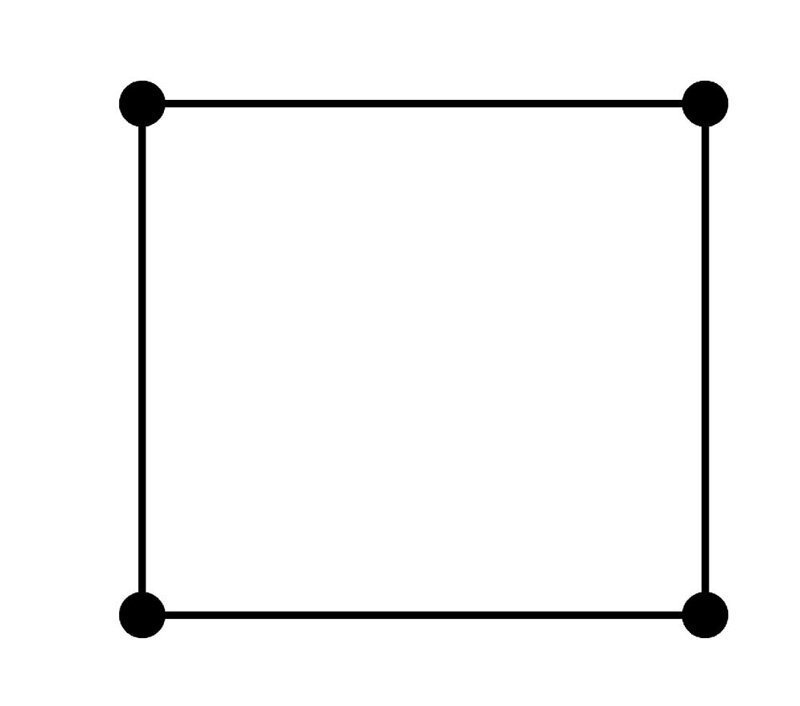
Источник:
С квадратом все намного проще, его определение звучит так: квадрат — это прямоугольник, у которого все стороны равны. Теперь нужно определить, что такое прямоугольник. Это тоже параллелограмм, как и ромб, но с прямыми углами, то есть равными 90º.
Основные свойства квадрата следующие:
1. Если провести биссектрисы всех углов квадрата (напомним, что углы прямые), то отрезки диагоналей квадрата будут лежать на этих биссектрисах.
2. Если провести диагонали между противоположными углами квадрата, то в центре симметрии квадрата, где эти диагонали пересекутся, они поделятся пополам.
3. Все отрезки диагоналей квадрата будут равны между собой.
Так в чем же отличие?

Источник:
Проще всего это понять и продемонстрировать ребенку с помощью спичек или зубочисток. Возьмите 4 спички и сделайте из них ромб. Обратите внимание на то, что у ромба разные углы: 2 острых и 2 тупых. А теперь превратите ромб в квадрат – просто сдвиньте спички таким образом, чтобы все углы стали прямыми, то есть по 90º.
Таким образом, получается, что квадрат – это как бы частный случай ромба (хотя настоящему специалисту это определение может показаться не совсем научным).
Еще одно отличие заключается в том, что у квадрата диагонали равны друг другу, а у ромба одна длиннее, а другая короче.
Вывод: каждый квадрат – это ромб с прямыми углами, но не каждый ромб – это квадрат.
Источник:
Ссылки по теме:

Понравился пост? Поддержи Фишки, нажми:
