Какими свойствами обладает биссектриса треугольника

Треугольникомназывается фигура,
которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков,
попарно соединяющих эти точки. Точки называются вершинамитреугольника,
а отрезки — его сторонами.

Виды треугольников

Треугольник называется равнобедренным,
если у него две сторны равны. Эти равные стороны называются боковыми
сторонами, а третья сторона называется основанием треугольника.

Треугольник, у которого все сторны равны, называется равносторонним
или правильным.

Треугольник
называется прямоугольным, если у него есть прямой угол, то есть
угол в 90°. Сторона прямоугольного треугольника, противолежащая прямому
углу, называется гипотенузой, две другие стороны называются катетами.

Треугольник называется остроугольным,
если все три его угла — острые, то есть меньше 90°.

Треугольник называется тупоугольным, если один из его углов —
тупой, то есть больше 90°.

Основные линии треугольника

Медиана

Медиана треугольника — это отрезок, соединяющий верщину треугольника
с серединой противолежащей стороны этого треугольника.

Свойства медиан треугольника

1. Медиана разбивает треугольник на два треугольника одинаковой площади.
2. Медианы треугольника пересекаются в одной точке, которая делит каждую
   из них в отношении 2:1, считая от вершины. Эта точка называется центром
   тяжести треугольника.
3. Весь треугольник разделяется своими медианами на шесть равновеликих
   треугольников.

Биссектриса

Биссектриса
угла — это луч, который исходит из его вершины, проходит между его
сторонами и делит данный угол пополам. Биссектрисой треугольника называется
отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на
противолежащей стороне этого треугольника.

Свойства биссектрис треугольника

1. Биссектриса угла — это геометрическое место точек, равноудаленных от
   сторон этого угла.
2. Биссектриса внутреннего угла треугольника делит противолежащую сторону
   на отрезки, пропорциональные прилегажащим сторонам: .
3. Точка пересечения биссектрис треугольника является центром
   окружности, вписанной в этот треугольник.

Высота

Высотой
треугольника называется перпендикуляр, проведенный из вершины треугольника
к прямой, содержащей противоположную сторону этого треугольника.

Свойства высот треугольника

1. В прямоугольном треугольнике высота, проведенная
   из вершины прямого угла, разбивает его на два треугольника, подобные
   исходному.
2. В остроугольном треугольнике две его
   высоты отсекают от него подобные треугольники.

Срединный перпендикуляр

Прямую, проходящую через середину отрезка перпендикулярно к нему, называют
серединным перпендикуляром к отрезку.

Свойства серединных перпендикуляров треугольника

1. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов
   этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная
   от концов отрезка, лежит на серединном перпендикуляре к нему.
2. Точка пересечения серединных перпендикуляров, проведенных к сторонам
   треугольника, является центром окружности,
   описанной около этого треугольника.

Средняя линия

Средней
линией треугольника называется отрезок, соединяющий середины двух его
сторон.

Свойство средней линии треугольника

Средняя линия треугольника параллельна одной из его сторон и равна половине
этой стороны.

Формулы и соотношения

Признаки равенства треугольников

Два треугольника равны, если у них соответственно равны:

• две стороны и угол между ними;
• два угла и прилежащая к ним сторона;
• три стороны.

Признаки равенства прямоугольных треугольников

Два прямоугольных треугольника равны, если
у них соответственно равны:

• гипотенуза и острый угол;
• катет и противолежащий угол;
• катет и прилежащий угол;
• два катета;
• гипотенуза и катет.

Подобие треугольников

Два треугольника подобны, если выполняется
одно из следующих условий, называемых признаками подобия:

• два угла одного треугольника равны двум углам другого треугольника;
• две стороны одного треугольника пропорциональны двум сторонам другого
  треугольника, а углы, образованные этими сторонами, равны;
• три стороны одного треугольника соответственно пропорциональны трем
  сторонам другого треугольника.

В подобных треугольниках соответствующие линии (высоты,
медианы, биссектрисы и
т. п.) пропорциональны.

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов, причем
коэффициент пропорциональности равен диаметру
описанной около треугольника окружности:

Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон
минус удвоенное произведение этих сторон на косинус угла между ними:

a2= b2+ c2—
2bc cos

Формулы площади треугольника

1. Произвольный треугольник

a, b, c — стороны;  —
угол между сторонами a и b;—
полупериметр; R — радиус описанной окружности; r — радиус
вписанной окружности; S — площадь; ha
— высота, проведенная к стороне a.

S
= aha

S = ab
sin

S = pr

2. Прямоугольный треугольник

a, b — катеты; c — гипотенуза; hc — высота,
проведенная к стороне c.

S = ab

S = chc

3. Равносторонний треугольник

Мы используем файлы cookie, чтобы персонализировать контент, адаптировать и оценивать результативность рекламы, а также обеспечить безопасность. Перейдя на сайт, вы соглашаетесь с использованием файлов cookie.

2 июня 2018

Сегодня будет очень лёгкий урок. Мы рассмотрим всего один объект — биссектрису угла — и докажем важнейшее её свойство, которое очень пригодится нам в будущем.

Только не надо расслабляться: иногда ученики, желающие получить высокий балл на том же ОГЭ или ЕГЭ, на первом занятии даже не могут точно сформулировать определение биссектрисы.

И вместо того, чтобы заниматься действительно интересными задачами, мы тратим время на такие простые вещи. Поэтому читайте, смотрите — и берите на вооружение.:)

Для начала немного странный вопрос: что такое угол? Правильно: угол — это просто два луча, выходящих из одной точки. Например:

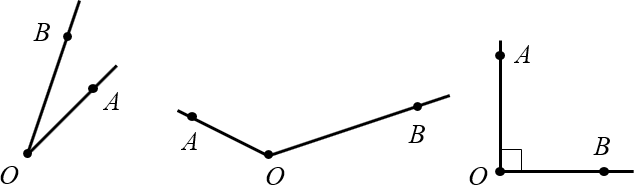Примеры углов: острый, тупой и прямой

Как видно из картинки, углы могут быть острыми, тупыми, прямыми — это сейчас неважно. Часто для удобства на каждом луче отмечают дополнительную точку и говорят, мол, перед нами угол $AOB$ (записывается как $angle AOB$).

Капитан очевидность как бы намекает, что помимо лучей $OA$ и $OB$ из точки $O$ всегда можно провести ещё кучу лучей. Но среди них будет один особенный — его-то и называют биссектрисой.

Определение. Биссектриса угла — это луч, который выходит из вершины этого угла и делит угол пополам.

Для приведённых выше углов биссектрисы будут выглядеть так:

Примеры биссектрис для острого, тупого и прямого угла

Поскольку на реальных чертежах далеко не всегда очевидно, что некий луч (в нашем случае это луч $OM$) разбивает исходный угол на два равных, в геометрии принято помечать равные углы одинаковым количеством дуг (у нас на чертеже это 1 дуга для острого угла, две — для тупого, три — для прямого).

Хорошо, с определением разобрались. Теперь нужно понять, какие свойства есть у биссектрисы.

Основное свойство биссектрисы угла

На самом деле у биссектрисы куча свойств. И мы обязательно рассмотрим их в следующем уроке. Но есть одна фишка, которую нужно понять прямо сейчас:

Теорема. Биссектриса угла — это геометрическое место точек, равноудалённых от сторон данного угла.

В переводе с математического на русский это означает сразу два факта:

1. Всякая точка, лежащая на биссектрисе некого угла, находится на одинаковом расстоянии от сторон этого угла.
2. И наоборот: если точка лежит на одинаковом расстоянии от сторон данного угла, то она гарантированно лежит на биссектрисе этого угла.

Прежде чем доказывать эти утверждения, давайте уточним один момент: а что, собственно, называется расстоянием от точки до стороны угла? Здесь нам поможет старое-доброе определение расстояния от точки до прямой:

Определение. Расстояние от точки до прямой — это длина перпендикуляра, проведённого из данной точки к этой прямой.

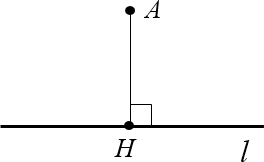
Например, рассмотрим прямую $l$ и точку $A$, не лежащую на этой прямой. Проведём перпендикуляр $AH$, где $Hin l$. Тогда длина этого перпендикуляра и будет расстоянием от точки $A$ до прямой $l$.

Графическое представление расстояния от точки до прямой

Поскольку угол — это просто два луча, а каждый луч — это кусок прямой, легко определить расстояние от точки до сторон угла. Это просто два перпендикуляра:

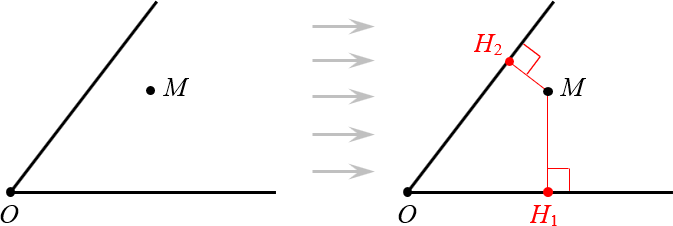Определяем расстояние от точки до сторон угла

Вот и всё! Теперь мы знаем, что такое расстояние и что такое биссектриса. Поэтому можно доказывать основное свойство.

Как и обещал, разобьём доказательство на две части:

1. Расстояния от точки на биссектрисе до сторон угла одинаковы

Рассмотрим произвольный угол с вершиной $O$ и биссектрисой $OM$:

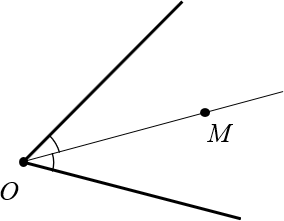
Докажем, что эта самая точка $M$ находится на одинаковом расстоянии от сторон угла.

Доказательство. Проведём из точки $M$ перпендикуляры к сторонам угла. Назовём их $M{{H}_{1}}$ и $M{{H}_{2}}$:

Провели перпендикуляры к сторонам угла

Получили два прямоугольных треугольника: $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$. У них общая гипотенуза $OM$ и равные углы:

1. $angle MO{{H}_{1}}=angle MO{{H}_{2}}$ по условию (поскольку $OM$ — биссектриса);
2. $angle M{{H}_{1}}O=angle M{{H}_{2}}O=90{}^circ $ по построению;
3. $angle OM{{H}_{1}}=angle OM{{H}_{2}}=90{}^circ -angle MO{{H}_{1}}$, поскольку сумма острых углов прямоугольного треугольника всегда равна 90 градусов.

Следовательно, треугольники равны по стороне и двум прилежащим углам (см. признаки равенства треугольников). Поэтому, в частности, $M{{H}_{2}}=M{{H}_{1}}$, т.е. расстояния от точки $O$ до сторон угла действительно равны. Что и требовалось доказать.:)

2. Если расстояния равны, то точка лежит на биссектрисе

Теперь обратная ситуация. Пусть дан угол $O$ и точка $M$, равноудалённая от сторон этого угла:

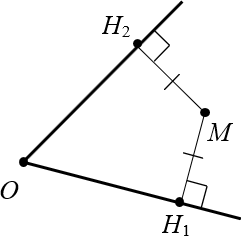
Докажем, что луч $OM$ — биссектриса, т.е. $angle MO{{H}_{1}}=angle MO{{H}_{2}}$.

Доказательство. Для начала проведём этот самый луч $OM$, иначе доказывать будет нечего:

Провели луч $OM$ внутри угла

Снова получили два прямоугольных треугольника: $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$. Очевидно, что они равны, поскольку:

1. Гипотенуза $OM$ — общая;
2. Катеты $M{{H}_{1}}=M{{H}_{2}}$ по условию (ведь точка $M$ равноудалена от сторон угла);
3. Оставшиеся катеты тоже равны, т.к. по теореме Пифагора $OH_{1}^{2}=OH_{2}^{2}=O{{M}^{2}}-MH_{1}^{2}$.

Следовательно, треугольники $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$ по трём сторонам. В частности, равны их углы: $angle MO{{H}_{1}}=angle MO{{H}_{2}}$. А это как раз и означает, что $OM$ — биссектриса.

В заключение доказательства отметим красными дугами образовавшиеся равные углы:

Биссектриса разбила угол $angle {{H}_{1}}O{{H}_{2}}$ на два равных

Как видите, ничего сложного. Мы доказали, что биссектриса угла — это геометрическое место точек, равноудалённых до сторон этого угла.:)

Теперь, когда мы более-менее определились с терминологией, пора переходить на новый уровень. В следующем уроке мы разберём более сложные свойства биссектрисы и научимся применять их для решения настоящих задач.

Смотрите также:

1. Высота в треугольнике
2. Основное свойство биссектрисы угла в треугольнике и его применение для решения задач
3. Тест к уроку «Площади многоугольников на координатной сетке» (легкий)
4. Правила вычисления производных
5. Сводный тест по задачам B15 (2 вариант)
6. Симметрия корней и оптимизация ответов в тригонометрии