Какими свойствами обладает бинарное отношение на множестве x y
Пусть R — некоторое бинарное отношение на множестве X, а х, у, z любые его элементы. Если элемент х находится в отношении R с элементом у, то пишут xRy.
1. Отношение R на множестве X называется рефлексивным, если каждый элемент множества находится в этом отношении с самим собой.
R —рефлексивно на X <=> xRx для любого x€ X
Если отношение R рефлексивно, то в каждой вершине графа имеется петля. Например, отношения равенства и параллельности для отрезков являются рефлексивными, а отношение перпендикулярности и «длиннее» не являются рефлексивными. Это отражают графы на рисунке 42.
2. Отношение R на множестве X называется симметричным, если из того, что элемент х находится в данном отношении с элементом у, следует, что элемент у находится в этом же отношении с элементом х.
R — симметрично на (хЯу =>у Rx)
Граф симметричного отношения содержит парные стрелки, идущие в противоположных направлениях. Отношения параллельности, перпендикулярности и равенства для отрезков обладают симметричностью, а отношение «длиннее» — не является симметричным (рис. 42).
3. Отношение R на множестве X называется антисимметричным, если для различных элементов х и у из множества X из того, что элемент х находится в данном отношении с элементом у, следует, что элемент у в этом отношении с элементом х не находится.
R — антисимметрично на Х« (xRy и xy ≠ yRx)
Замечание: черта сверху обозначает отрицание высказывания.
На графе антисимметричного отношения две точки может соединять только одна стрелка. Примером такого отношения является отношение «длиннее» для отрезков (рис. 42). Отношения параллельности, перпендикулярности и равенства не являются антисимметричными. Существуют отношения, не являющиеся ни симметричными, ни антисимметричными, например отношение «быть братом» (рис. 40).
4. Отношение R на множестве X называется транзитивным, если из того, что элемент х находится в данном отношении с элементом у и элемент у находится в этом лее отношении с элементом z, следует, что элемент х находится в данном отношении с элементом Z
R — транзитивно на A≠ (xRy и yRz=> xRz)
На графах отношений «длиннее», параллельности и равенства на рисунке 42 можно заметить, что если стрелка идет от первого элемента ко второму и от второго к третьему, то обязательно есть стрелка, идущая от первого элемента к третьему. Эти отношения являются транзитивными. Перпендикулярность отрезков не обладает свойством транзитивности.
Существуют и другие свойства отношений между элементами одного множества, которые мы не рассматриваем.
Одно и то же отношение может обладать несколькими свойствами. Так, например, на множестве отрезков отношение «равно» — рефлексивно, симметрично, транзитивно; отношение «больше» — антисимметрично и транзитивно.
Если отношение на множестве X рефлексивно, симметрично и транзитивно, то оно является отношением эквивалентности на этом множестве. Такие отношения разбивают множество X на классы.
Данные отношения проявляются, например, при выполнении заданий: «Подбери полоски равные по длине и разложи по группам», «Разложи мячи так, чтобы в каждой коробке были мячи одного цвета». Отношения эквивалентности («быть равным по длине», «быть одного цвета») определяют в данном случае разбиение множеств полосок и мячей на классы.
Если отношение на множестве 1 транзитивно и антисимметрично, то оно называется отношением порядка на этом множестве.
Множество с заданным на нем отношением порядка называется упорядоченным множеством.
Например, выполняя задания: «Сравни полоски по ширине и разложи их от самой узкой до самой широкой», «Сравни числа и разложи числовые карточки по порядку», дети упорядочивают элементы множеств полосок и числовых карточек при помощи отношений порядка; «быть шире», «следовать за».
Вообще отношения эквивалентности и порядка играют большую роль в формировании у детей правильных представлений о классификации и упорядочении множеств. Кроме того, встречается много других отношений, которые не являются ни отношениями эквивалентности, ни отношениями порядка.
6. Что такое характеристическое свойство множества?
7. В каких отношениях могут находиться множества? Дайте пояснения каждому случаю и изобразите их при помощи кругов Эйлера.
8. Дайте определение подмножества. Приведите пример множеств, одно из которых является подмножеством другого. Запишите их отношение при помощи символов.
9. Дайте определение равных множеств. Приведите примеры двух равных множеств. Запишите их отношение при помощи символов.
10. Дайте определение пересечения двух множеств и изобразите его при помощи кругов Эйлера для каждого частного случая.
11. Дайте определение объединения двух множеств и изобразите его при помощи кругов Эйлера для каждого частного случая.
12. Дайте определение разности двух множеств и изобразите ее при помощи кругов Эйлера для каждого частного случая.
13. Дайте определение дополнения и изобразите его при помощи кругов Эйлера.
14. Что называется разбиением множества на классы? Назовите условия правильной классификации.
15. Что называется соответствием между двумя множествами? Назовите способы задания соответствий.
16. Какое соответствие называется взаимно однозначным?
17. Какие множества называют равномощными?
18. Какие множества называют равночисленными?
19. Назовите способы задания отношений на множестве.
20. Какое отношение на множестве называют рефлексивным?
21. Какое отношение на множестве называют симметричным?
22. Какое отношение на множестве называют антисимметричным?
23. Какое отношение на множестве называют транзитивным?
24. Дайте определение отношения эквивалентности.
25. Дайте определение отношения порядка.
26. Какое множество называют упорядоченным?
Способы задания бинарного отношения
Определение бинарного отношения
Бинарные отношения
Пусть среди трех людей: Андрей (А), Василий (В) и Сергей (С) двое знакомы друг с другом (Андрей и Василий) и знают третьего – Сергея, но Сергей их не знает. Как описать отношения между этими людьми?
Имеем исходное множество Х = {А, В, С}. Далее из элементов множества Х составим упорядоченные пары:
(А, В), (В, А), (А, С), (В, С). Это множество пар и описывает связи между элементами множества X. Кроме того, множество этих пар есть подмножество декартова произведения X ´ X.
Определение. На множестве X задано бинарное отношение R, если задано подмножество декартова произведения X ´ X (т. е. R Ì X ´ X).
Пример 1. Пусть X = {1, 2, 3, 4}. Зададим на X следующие отношения:
Т = {(х, у) | х, у Î Х; х = у} – отношение равенства;
Р = {(х, у) | х, у Î Х; х = у — 1} – отношение
предшествования;
Q = {(х, у) | х, у Î Х; х делится на у} – отношение
делимости.
Все эти отношения заданы с помощью характеристического свойства. Перечислим элементы этих отношений для заданного множества X = {1,2,3,4}:
Т = {(1,1), (2,2), (3,3), (4,4)};
P = {(1,2), (2,3), (3,4) };
Q = {(4,4), (4,2), (4,1), (3,3), (3,1), (2,2), (2,1), (1,1)}.
Тот факт, что пара (х, у) принадлежит данному отношению R, будем записывать: (х, у) Î R или xRy. Например, для отношения Q запись 4Q2 означает, что 4 делится на 2 нацело, т. е. (4,2) Î Q.
Областью определения Dr бинарного отношения R называется множество DR = {x | (х, у) Î R}.
Областью значений ЕR бинарного отношения R называется множество ЕR = {у| (х, у) Î R}.
В примере для отношения Р областью определения является множество DR = {1,2,3}, а областью значений является множество ЕR = {2,3,4}.
Бинарное отношение можно задать, указав характеристическое свойство или перечислив все его элементы. Существуют и более наглядные способы задания бинарного отношения: график отношения, схема отношения, граф отношения, матрица отношения.
График отношения изображается в декартовой системе координат: на горизонтальной оси отмечается область определения, на вертикальной — область значений отношения. Элементу отношения (х, у) соответствует точка плоскости с этими координатами.
a б
Рис. 1.8. График отношения Q (а) и схема отношения Q (б)
Схема отношения изображается с помощью двух вертикальных прямых, левая из которых соответствует области определения отношения, а правая – множеству значений отношения. Если элемент (х, у) принадлежит отношению R, то соответствующие точки из DR и ЕR соединяются прямой.
Граф отношения R Ì X ´ X строится следующим образом. На плоскости в произвольном порядке изображаются точки — элементы множества X. Пара точек х и у соединяется дугой (линией со стрелкой) тогда и только тогда, когда пара (х, у) принадлежит отношению R.
Матрица отношения R Ì X ´ X – это квадратная таблица, каждая строка и столбец которой соответствует некоторому элементу множества X. На пересечении строки х и столбца у ставится 1, если пара (х, у) Î R; все остальные элементы матрицы заполняются нулями. Элементы матрицы нумеруются двумя индексами, первый равен номеру строки, второй – номеру столбца.
Пусть X = {х1, х2, …, хn} . Тогда матрица отношения
R Ì X ´ X имеет n строк и n столбцов, а ее элемент rij определяется по правилу:
1, если (xi, yj) Î R, где i = l, 2, …, n; j = l, 2, …, n.
0, если (xi, yj) Ï R.
Рис. 1.9. Граф отношения Q (а) и матрица отношения Q (б)
1. Отношение R на множестве X называется рефлексивным, если для всех х Î X выполняется условие (х, х) Î R. Отношение R на множестве Х называется нерефлексивным, если условие (х, х) Î R не выполняется хотя бы при одном х Î X .
2. Отношение R на множестве X называется симметричным, если из условия (х, у) Î R следует
(у, х) Î R. Отношение R на множестве X называется несимметричным, если для любых х, у Î X из условия (х, y) Î R следует (у, х) Ï R.
3. Отношение R на множестве X называется транзитивным, если для любых х, у, z Î R из одновременного выполнения условий (x, y) Î R и (у, z) Î R следует (х, z) Î R .
Пример. Рассмотрим следующие отношения на множестве X = {1,2,3,4,5,6,7}:
G = {(x, y) | х, у Î Х; х > у};
L = {(х, у) | х, у Î Х; х £ у};
M = {(x, y) | х, у Î X; (х — у) делится на 3};
К = {(х, y) | х, у Î Х; х2 + у2 £ 20}.
Исследуем, какими свойствами они обладают.
Среди приведенных в примере отношений рефлексивнымиявляются отношение L (т. к. х £ х справедливо при всех х Î X) и отношение М (т. к. х — х = 0 делится на 3, поэтому пара (х, х) принадлежит отношению М при всех х Î X).
Симметричными являются отношения М (если х — у делится на 3, то и у — х делится на 3) и К (если х2 + у2 £20, то и у2 + х2 £ 20).
Транзитивными являются отношения G, L, М.
Рассмотрим отношение «уважать», определенное на множестве всех людей %%M%%. Для полной информации о том, кто кого уважает, составим следующее множество %%R%%. Переберем все пары %%(a, b)%%, где %%a, b%% пробегают множество всех людей. Если %%a%% уважает %%b%%, то пару %%(a,b)%% отнесем к множеству %%R%%, иначе — нет.
Этот список полностью отражает отношение «уважать». Если нужно узнать, уважает ли человек %%a%% человека %%b%%, то просмотрим множество %%R%%. Если пара %%(a, b) in R%%, то заключаем, что %%a%% уважает %%b%%. В случае %%(a,b) notin R%% — %%a%% не уважает %%b%%.
Определение
Бинарным отношением, определенным на множестве %%M%%, называется произвольное подмножество %%R%% из декартового произведения %%M^2%%.
Пример
Рассмотрим отношение больше на множестве %%M = {1, 2}%%. Тогда
$$
M^2 = big{(1, 1), (1,2), (2,1), (2,2)big}
$$
Из него выбирем все пары %%(a,b)%%, где %%a > b%%. Получим
$$
R = big{(2,1)big}
$$
Виды бинарных отношений
Рефлексивное бинарное отношение
Бинарное отношение %%R%% на множестве %%M%% называется рефлексивным,
если для любого элемента %%a%% из %%M%%, выполняется условие %%a~R~a%%.
$$
begin{array}{l}
forall ain M~~a~R~a text{ или}\
forall ain M~~(a,a) in R.
end{array}
$$
Примеры
- Рассмотрим отношение больше на множестве действительных чисел. Является ли отношение больше рефлексивным? Если да, то каждое число является больше самого себя, что неверно. Поэтому отношение больше не рефлексивно.
- Рассмотрим отношение равно на множестве действительных чисел. Оно является рефлексивным, так как каждое действительное число равно самому себе.
Симметричное бинарное отношение
Бинарное отношение %%R%% на множестве %%M%% называется симметричным,
если для любых двух элементов %%a, b%% из %%M%%, из условия %%a~R~b%% следует условие %%b~R~a%%.
$$
begin{array}{l}
forall a,bin M~~a~R~b rightarrow b~R~a text{ или}\
forall a,bin M~~(a,b) in R rightarrow (b,a) in R.
end{array}
$$
Примеры
- Рассмотрим отношение больше на множестве действительных чисел. Является ли отношение больше симметричным? Оно не является симметричным, так как если %%a > b%%, то условие %%b > a%% не выполняется. Поэтому отношение больше не симметрично.
- Пусть %%R%% — отношение, определенное на множестве %%M = {a,b,c}%%. При этом %%R = big{ (a,b), (b,c), (a,a), (b,a), (c,b)big}%%. Для этого отношения имеем %%forall x,y in M ~~ (x,y) in R rightarrow (y,x) in R%%. По определению %%R%% симметрично.
Транзитивное бинарное отношение
Бинарное отношение %%R%% на множестве %%M%% называется транзитивным,
если для любых элементов %%a, b, c%% из %%M%%, из условий %%a~R~b%% и %%b~R~c%% следует условие %%a~R~c%%.
$$
begin{array}{l}
forall a,b,cin M~~a~R~b land b~R~c rightarrow a~R~c text{ или}\
forall a,b,cin M~~(a,b) in R land (b,c) in R rightarrow (a,c) in R.
end{array}
$$
Пример
Рассмотрим отношение больше на множестве дейтсвительных чисел. Оно является транзитивным, так как для любых элементов выполняется условние %%forall a,b,cin M~~a > b land b > c rightarrow a > c%%. Так, например, подставив вместо %%a, b%% и %%c%% числа %%2, 1%% и %%0%% соответственно, получим: если %%2 > 1%% и %%1 > 0%%, то %%2 > 0%% — верное утверждение (вспомните импликацию, из истины следует истина).
Антисимметричное бинарное отношение
Бинарное отношение %%R%% на множестве %%M%% называется антисимметричным,
если для любых элементов %%a, b%% из %%M%%, из условий %%a~R~b%% и %%b~R~a%% следует условие %%a = b%%.
$$
begin{array}{l}
forall a,b,cin M~~a~R~b land b~R~a rightarrow a = b text{ или}\
forall a,bin M~~(a,b) in R land (b,a) in R rightarrow a = b.
end{array}
$$
Пример
Отношение больше или равно на множестве действительных чисел антисимметрично. Действительно, если %%a geq b%% и %%b geq a%%, %%a = b%%.
Эквивалентное бинарное отношение
Бинарное отношение %%R%% на множестве %%M%% называется отношением эквивалентности,
если оно рефлексивно, симметрично и транзитивно.
Нетрудно проверить, что отношение параллельности на множестве прямых плоскости является отношением эквивалентности.
Отношение частичного порядка
Бинарное отношение %%R%% на множестве %%M%% называется отношением частичного порядка,
если оно рефлексивно, антисимметрично и транзитивно.
Отношение больше или равно на множестве действительных чисел является отношением частичного порядка.
Построение отрицаний
Пусть %%R%% — бинарное отношение на множестве %%M%%, и %%P%% — одно из следующих условий:
- отношение %%R%% рефлексивно,
- отношение %%R%% симметрично,
- отношение %%R%% транзитивно,
- отношение %%R%% антисимметрично.
Построим для каждого из них отрицание выполнения условия %%P%%.
Отрицание рефлексивности
По определению %%R%% рефлексивно, если каждый элемент множества %%M%% находится в отношении %%R%% к самому себе, то есть %%forall a in M~~a~R~a%%. Тогда рассмотрим отрицание рефлексивности как истинное высказывание %%overline{forall a in M~~a~R~a}%%. Используем равносильность %%overline{forall x P(x)} equiv exists x overline {P(x)}%%. В нашем случае получаем %%forall a in M~~a~R~a equiv exists ain M~~a~nottext{R }~a%%, что и нужно.
Аналогично получаем и остальные отрицания. В итоге получаем следующие утверждения:
%%R%% не рефлексивно тогда и только тогда, когда
$$
exists a in M~~a~not R~a
$$%%R%% не симметрично тогда и только тогда, когда
$$
exists a, b in M~~ a~R~b land b~not R~a
$$%%R%% не транзитивно тогда и только тогда, когда
$$
exists a, b, c in M a~R~b land b~R~c land a~not R~c
$$%%R%% не антисимметрично тогда и только тогда, когда
$$
exists a, b in M~~ a~R~b land b~R~a land a neq b.
$$
План
1. Свойство рефлексивености
2. Свойство симметричности
3. Свойство транзитивности
Свойства отношений
Мы установили, что бинарное отношение на множестве X представляет собой множество упорядоченных пар элементов, принадлежащих декартову произведению X х Х. Это математическая сущность всякого отношения. Но, как и любые другие понятия, отношения обладают свойствами. Их удалось выделить, изучая различные конкретные отношения. Свойств достаточно много, в нашем курсе мы будем изучать только некоторые.
Рассмотрим на множестве отрезков, представленных на рис. 98, отношения перпендикулярности, равенства и «длиннее». Построим графы этих отношений (рис. 99) и будем их сравнивать. Видим, что граф отношения равенства отличается от двух других наличием петель в каждой его вершине. Эти петли — результат того, что отношение равенства отрезков обладает свойством: любой отрезок равен самому себе. Говорят, что отношение равенства обладает свойством рефлексивности или просто, что оно рефлексивно.
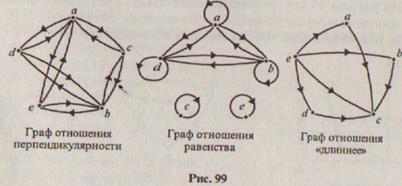
Определение. Отношение R на множестве X называется рефлексивным, если о каждом элементе множества X можно сказать, что он находится в отношении R с самим собой.
Используя символы, это отношение можно записать в таком виде:
R рефлексивно на Х ↔ х R х для любого х € X.
опр.
Если отношение R рефлексивно на множестве X, то в каждой вершине графа данного отношения имеется петля. Справедливо и обратное утверждение: граф, каждая вершина которого имеет петлю, задает отношения, обладающие свойством рефлексивности.
Примеры рефлексивных отношений:
— отношение «кратно» на множестве натуральных чисел (каждое натуральное число кратно самому себе);
— отношение подобия треугольников (каждый треугольник подобен самому себе).
Существуют отношения, которые свойством рефлексивности не обладают. Таким, например, является отношение перпендикулярности на множестве отрезков: нет ни одного отрезка, о котором можно сказать, что он перпендикулярен самому себе. Поэтому на графе отношения перпендикулярности (рис. 99) нет ни одной петли. Не обладает свойством рефлексивности и отношение «длиннее» для отрезков.
Обратим теперь внимание на графы отношений перпендикулярности и равенства отрезков. Они «похожи» тем, что если есть одна стрелка, соединяющая пару элементов, то обязательно есть и другая, соединяющая те же элементы, но идущая в противоположном направлении. Эта особенность графа отражает те свойства, которыми обладают отношения параллельности и равенства отрезков:
— если один отрезок перпендикулярен другому отрезку, то этот «другой» перпендикулярен первому;
— если один отрезок равен другому отрезку, то этот «другой» равен первому.
Про отношения перпендикулярности и равенства отрезков говорят, что они обладают свойством симметричности или просто симметричны.
Определение. Отношение R на множестве X называется симметричным, если выполняется условие: из того, что элемент х находится в отношении R с элементом у, следует, что и элементу находится в отношении R с элементом х.
Используя символы, это отношение можно записать в таком виде:
R симметрично на Х ↔ (х R y →yRx).
опр.
Граф симметричного отношения обладает особенностью: вместе с каждой стрелкой, идущей от х к у, граф содержит и стрелку, идущую от у к x. Справедливо и обратноеутверждение. Граф, содержащий вместе с каждой стрелкой, идущей от x к у, и стрелку, идущую от у к x, является графом симметричного отношения.
В дополнение к рассмотренным двум примерам симметричных отношений присоединим еще такие:
-отношениепараллельности на множестве прямых (если прямая x параллельна прямой у, то и прямая у параллельна прямой х)
-отношение подобия треугольников (если треугольник F подобен треугольнику Р, то треугольник Р подобен треугольнику F).
Существуют отношения, которые свойством симметричности не обладают. Таким, например, является отношение «длиннее» на множестве отрезков. Действительно, если отрезок x длиннее отрезка у, то отрезок у не может быть длиннее отрезка х. Про отношения «длиннее» говорят, что оно обладает свойством антисимметричности или просто антисимметрично.
Определение. Отношение R на множестве X называется антисимметричным, если для различных элементов х и у из множества X выполнено условие: из того, что х находится в отношении R с элементом у, следует, что элемент у в отношении R с элементом х не находится.
Используя символы, это определение можно записать в таком виде:
R симметрично на Х ↔ (х R y ^ x≠y →yRx).
опр.
Граф антисимметричного отношения обладает особенностью: если две вершины графа соединены стрелкой, то эта стрелка только одна. Справедливо и обратное утверждение: граф, вершины которого соединены только одной стрелкой, есть граф антисимметричного отношения.
Кроме отношения «длиннее» на множестве отрезков свойством антисимметричности, например, обладают:
— отношение «больше» для чисел (если х больше у, то у не может
быть больше х);
— отношение «больше на 2» для чисел (если х больше у на 2, то у не может быть больше на 2 числа х),
Существуют отношения, не обладающие ни свойством симметричности, ни свойством антисимметричности. Рассмотрим, например, отношение «быть сестрой» на множестве детей одной семьи. Пусть в семье трое детей: Катя, Маша и Толя. Тогда граф отношения «быть сестрой» будет таким, как на рисунке 100. Он показывает, что данное отношение не обладает ни свойством симметричности, ни свойством антисимметричности.
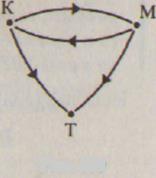
Рис.100
Обратим внимание еще раз на одну особенность графа отношения «длиннее» (рис. 99). На нем можно заметить: если стрелки проведены от е к а и от а к с, то есть стрелка от е к с; если стрелки приведены от е к b и от b к с, то есть стрелка и от е к с и т.д. Эта особенность графа отражает важное свойство отношения «длиннее»: если первый отрезок длиннее второго, а второй — длиннее третьего, то первый — длиннее третьего. Говорят, что это отношение обладает свойством транзитивности или просто транзитивно.
Определение. Отношение R на множестве X называется транзитивным, если выполняется условие; из того, что элемент х находится в отношении R с элементом у и элемент у находится в отношении R с элементом z, следует, что элемент х находится в отношении К с элементом z .
Используя символы, это определение можно записать в таком виде:
R транзитивно на X ↔ (х R y ^ yRz → xRz).
опр.
Граф транзитивного отношения с каждой парой стрелок, идущих от x к у и у к z, содержит стрелку, идущую от х к z. Справедливо и обратное утверждение.
Кроме отношения «длиннее» на множестве отрезков свойством транзитивности обладает отношение равенства: если отрезок х равен отрезку у и отрезок у равен отрезку z, то отрезок х равен отрезку z, Это свойство отражено и на графе отношения равенства (рис. 99)
Существуют отношения, которые свойством транзитивности не обладают. Таким отношением является, например, отношение перпендикулярности: если отрезок а перпендикулярен отрезку d, а отрезок d перпендикулярен отрезку b, то отрезки а и b не перпендикулярны!
Рассмотрим еще одно свойство отношений, которое называют свойством связанности, а отношение, обладающее им, называют связанным.
Определение. Отношение R на множестве X называется связанным, если для любых элементов х и у из множества X выполняется условие: из того, что х и у различны, следует, что либо х находится в отношении R с элементом у, либо элемент у находится в отношении R с элементом х.
Используя символы, это определение можно записать в таком виде:
R связано на множестве X ↔ (х ≠ у => хRу v уRх).
опр.
Например, свойством связанности обладают отношения «больше» длянатуральных чисел: для любых различных чисел х и у можно утверждать, что либо х > у, либо у > х.
На графе связанного отношения любые две вершины соединены стрелкой. Справедливо и обратное утверждение.
Существуют отношения, которые свойством связанности не обладают. Таким отношением, например, является отношение делимости на множестве натуральных чисел: можно назвать такие числа х и у, что ни число х не является делителем числа у, ни число у не является делителем числа х.
Выделенные свойства позволяют анализировать различные отношения с общих позиций — наличия (или отсутствия) у них тех или иных свойств.
Так, если суммировать все сказанное об отношении равенства, заданном на множестве отрезков (рис. 99), то получается, что оно рефлексивно, симметрично и транзитивно. Отношение «длиннее» на том же множестве отрезков антисимметрично и транзитивно, а отношение перпендикулярности — симметрично, но оно не обладает свойствами рефлексивности и транзитивности. Все эти отношения на заданном множестве отрезков связанными не являются.
Задача 1. Сформулировать свойства отношения R, заданного при помощи графа (рис. 101).
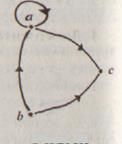
Рис.101
Решение. Отношение R-антисимметрично, так как вершины графа соединяются только одной стрелкой.
Отношение R — транзитивно, так как с парой стрелок, идущих от b к а и от а к с, на графе есть стрелка, идущая от b к с.
Отношение R — связанно, так как любые две вершины соединены стрелкой.
Отношение R свойством рефлексивности не обладает, так как на графе есть вершины, в которых петли нет.
Задача 2. Сформулировать свойства отношения «больше в 2 раза», заданного на множестве натуральных чисел.
Решение. «Больше в 2 раза» — это краткая форма отношения «число х больше числа у в 2 раза». Это отношение антисимметрично, так как выполняется условие: из того, что число х больше числа у в 2 раза, следует, что число y не больше числа x 2 раза.
Данное отношение не обладает свойством рефлексивности, потому что ни про одно число нельзя сказать, что оно больше самого себя в 2 раза.
Заданное отношение не транзитивно, так как из того, что число x больше числа у на 2, а число у больше числа z на 2, следует, что число х не может быть больше числа z на 2.
Это отношение на множестве натуральных чисел свойством связанности не обладает, так как существуют пары таких чисел х и у, что ни число х не больше числа у в два раза, ни число у не больше х в 2 раза. Например, это числа 7 и 3, 5 и 8 и др.
Упражнения
1.Докажите, что отношение R, заданное при помощи графа (рис.102), рефлексивно, антисимметрично и транзитивно.
2.Докажите, что отношение Т, заданное при помощи графа (рис.103), симметрично и транзитивно.
3.Сформулируйте условия, при которых отношение свойством рефлексивности не обладает, и докажите, что отношение Т (см. упр. 2) не рефлексивно.
4. Сформулируйте условия, при которых отношение не обладает свойством: а) симметричности; б) антисимметричности; в)транзитивности; г) связанности.
5. 
Докажите, что отношение Р, граф которого изображен на рисунке 104, не обладает ни свойством симметричности, ни свойством антисимметричности, ни свойством транзитивности.
6.Какими свойствами обладает отношение, граф которого изображен на рисунке 105? Является ли оно рефлексивным? Транзитивным?
7.Какие из следующих утверждений истинны:
а) Отношение «x больше у на 3» антисимметрично на множестве N, так как из того, что х больше у на 3, не следует, что у больше х на 3.
б) Отношение «x больше у на 3» антисимметрично, так как из того, что х больше у на 3, следует, что у не больше х на 3.
в) Отношение «х больше у на 3» антисимметрично, так как из того, что х больше у на 3, следует, что у меньше х на 3.
8. На множестве отрезков задано отношение «короче». Верно ли, что оно антисимметрично
и транзитивно? Рефлексивно ли оно?
9. Какими свойствами обладают следующие отношения, заданные на множестве натуральных чисел:
а) «меньше»; б) «меньше на 2»; в) «меньше в 2 раза»?
10. На множестве X ={а, b, с}задано отношение R = {(а, b), (а, а), (b,b), (с, с), (b, а), (b, с), (с, b)}.Какими свойствами оно обладает?
11. На множестве Х= {2,4,6,8, 12} заданы отношения «больше» и «кратно». В чём их сходство и различие?
12.Установите, какое отношение рассматривается в задаче; какие приемы анализа задачи можно использовать:
а) Школьники сделали к карнавалу 15 шапочек для мальчиков, адля девочек в 2 раза больше. Сколько всего карнавальных шапочек они сделали?
б) Второклассники вырезали для елки 26 звездочек, это в 2 раза меньше, чем снежинок. Сколько всего звездочек и снежинок вырезали второклассники?