Какими свойствами или свойством не обладает выборочная дисперсия
Пусть наблюдаемая случайная величина имеет математическое ожидание и дисперсию .
I. Свойства выборочного среднего , как точечной оценки неизвестного математического ожидания.
1. Выборочное среднее является несмещенной оценкой неизвестного математического ожидания .
.
2. Выборочное среднее является состоятельной оценкой неизвестного математического ожидания .
Рассмотрим два способа доказательства этого свойства.
а) Последовательность независимых одинаково распределенных случайных величин , имеющих конечные математическое ожидание и дисперсиюподчиняется закону больших чисел, в соответствии с которым
.
б) Поскольку выборочное среднее является несмещенной оценкой неизвестного математического ожидания , то для доказательства состоятельности достаточно показать, что . А это следует из свойства аддитивности дисперсии для независимых случайных величин имеем:
.
3. Если закон распределения наблюдаемой случайной величины является нормальным с параметрами (то есть с неизвестным математическим ожиданием и известной дисперсией ), то выборочное среднее является эффективной оценкой параметра .
Покажем, что выборочное среднее обращает неравенство Рао-Крамера в равенство.
Для этого вычислим информацию Фишера о параметре , содержащуюся в одном наблюдении над случайной величиной :
.
Плотность вероятностей наблюдаемой случайной величины имеет вид:
,
а ее логарифм . Дифференцируя по , получаем:
.
Подставляя вместо аргумента случайную величину , для информации Фишера получаем выражение:
.
Следовательно,
.
Свойство 3 остается справедливым и в общей нормальной модели , когда неизвестны и математическое ожидание, и дисперсия.
II. Свойства выборочной дисперсии , как точечной оценки неизвестной дисперсии.
1. Выборочная дисперсия не является несмещенной оценкой неизвестной дисперсии . Она является асимптотически несмещенной оценкой .
Найдем математическое ожидание :
(поскольку при в силу независимости случайных величин )
.
Таким образом, выборочная дисперсия не является несмещенной оценкой дисперсии . Ее смещение . Поскольку , то выборочная дисперсия является асимптотически несмещенной оценкой дисперсии .
Несмещенную оценку дисперсии можно получить, умножив на коэффициент , компенсирующий ее смещение.
Несмещенная оценка дисперсии
называется исправленной выборочной дисперсией.
На практике исправленную выборочную дисперсию , как точечную оценку неизвестной дисперсии , используют чаще, чем просто выборочную дисперсию . Однако при больших оценки и отличаются крайне незначительно.
2. Выборочная дисперсия и исправленная выборочная дисперсия являются состоятельными оценками неизвестной дисперсии .
Как отмечалось ранее
.
В силу закона больших чисел , а . Поэтому
.
Поскольку при больших , то состоятельной оценкой дисперсии является и исправленная выборочная дисперсия .
3. Если закон распределения наблюдаемой случайной величины является нормальным с неизвестными параметрами , то исправленная выборочная дисперсия является асимптотически эффективной оценкой неизвестной дисперсии , то есть
,
где — эффективная оценка неизвестной дисперсии (без доказательства).
Поскольку при больших , то асимптотически эффективной оценкой дисперсии является и выборочная дисперсия .
На предыдущем уроке по математической статистике мы изучили центральные показатели статистической совокупности, а именно моду, медиану, среднюю, и теперь переходим к показателям вариации. Они показывают, КАК варьируются статистические данные, а именно – насколько далеко «разбросаны» варианты относительно средних значений, да и просто друг от друга. В данной статье будут рассмотрены самые популярные показатели, и для опытных читателей сразу оглавление:
- Размах вариации
- Среднее линейное (абсолютное) отклонение
- Генеральная и выборочная дисперсия, тут же исправленная выборочная дисперсия
и, чтобы не «лепить» километровую простыню, разделю материал на две веб страницы:
- Во второй части будет формула для вычисления дисперсии, среднее квадратическое (стандартное) отклонение и коэффициент вариации.
Итак, прямо сейчас мы сформулируем определения этих показателей, узнаем соответствующие формулы и, конечно, потренируемся в конкретных вычислениях. Да не просто в конкретных, а в рациональных.
Но прежде систематизируем информацию о том, какие статистические данные могут оказаться в нашем распоряжении:
– они могут быть первичными (не обработанными), грубо говоря – это неупорядоченный список чисел, либо вторичными – это уже сформированный дискретный (Урок 2) или интервальный вариационный ряд (Урок 3).
– рассматриваемая статистическая совокупность может быть генеральной либо выборочной, и чаще, конечно, перед нами выборка.
…что-то не понятно по терминам? Срочно изучать основы предмета (Урок 1)! – это быстро и интересно, ну а я, сколько нужно, вас тут подожду 🙂
Размах вариации
Он уже встречался. Это разность между самым большим и самым малым значением статической совокупности:
при этом не имеет значения, генеральная ли нам дана совокупность или выборочная, сгруппированы ли данные или нет.
Очевидно, что все варианты исследуемой совокупности (той или иной) заключены в отрезке , а размах – есть не что иное, как его длина.
Такой вот простой, надёжный и понятный показатель. Но, несмотря на его элементарность, рассмотрим технику вычисления, и, конечно, это отличный повод размяться:
Пример 12
Дана статистическая совокупность
15, 17, 13, 10, 21, 17, 23, 9, 14, 19
Найти размах вариации
Решить задачу можно несколькими способами.
Способ первый, суровый – продолжаю вас готовить к борьбе с киборгами :)) Это когда под рукой нет вычислительной техники. Или когда она есть, но вы сами понимаете, как важно «прокачать» свои человеческие способности.
Если чисел не так много (наш случай), то максимальное и минимальное значения легко углядеть устно: и размах равен: единиц.
Если чисел больше (20-30 и даже больше), то надёжен следующий алгоритм:
1) Ищем минимальное значение. Сначала самым маленьким будет первое число: 15. Второе число (17) больше, и поэтому его пропускаем. Третье число (13) меньше, чем 15, и теперь 13 – самое малое число. И так далее, пока не закончится список.
2) Ищем максимальное значение. Сначала самым большим будет первое число: 15. Второе число (17) больше и теперь оно становится самым большим. И так далее – до конца списка.
Способ второй, более быстрый (обычно). Использование программного обеспечения, при этом числа можно просто отсортировать (по возрастанию либо убыванию) или использовать специальные функции:
Задание 6
Найти минимальное и минимальное значения в Экселе – данные уже там, данные вас ждут!
…отлично, молодцы!
Запишем ответ ед. и с нетерпением перейдём к другим показателям, которые характеризуют степень рассеяния вариант относительно центра совокупности, прежде всего, относительно средней.
О смысле и важности этих показателей я рассказал в курсе теории вероятностей (статья о дисперсии дискретной случайной величины), но коротко повторю и сейчас. Рассмотрим двух студентов, каждый из которых в среднем учится на 3,5 балла. Но есть один нюанс. Один стабильно получает тройки-четвёрки, а другой то пятёрки, то двойки. И поэтому важно знать меру рассеяния оценок относительно средней величины. Чем она меньше – тем стабильнее учится студент.
Эту меру можно оценить следующим образом: из каждой оценки (пусть их будет штук) вычитаем среднее значение . Величина называется отклонением (значения ) от средней.
Теперь эти отклонения нужно просуммировать, но тут появляется проблема: среди разностей есть как положительные, так и отрицательные, и при их суммировании будет происходить взаимоуничтожение отклонений. Более того, итоговая сумма равна нулю: , и мы не получаем желаемого результата.
Вопрос можно решить с помощью модуля, который уничтожает минусы: , после чего осталось разделить сумму на объём совокупности и получить:
среднее линейное отклонение
– есть среднее арифметическое абсолютных отклонений всех значений статистической совокупности от средней. Это формула для несгруппированных статистических данных.
Если же в нашем распоряжении есть сформированный дискретный либо интервальный вариационный ряд, то формула будет такой:
, где – варианты (для дискретного ряда) либо середины частичных интервалов (для интервального ряда), а – соответствующие частоты.
Напоминаю, что маленькая буква обычно используется для выборочной совокупности, а большая – для генеральной: – объём ген. совокупности, – частоты.
И начнём мы с малого:
Пример 13
В результате 10 независимых измерений некоторой величины, выполненных с одинаковой точностью, полученные опытные данные, которые представлены в таблице
Требуется вычислить среднее линейное отклонение
Решение: очевидно, что перед нами первичные данные и выборочная совокупность (теоретически измерений можно провести бесконечно много). На первом шаге вычислим выборочную среднюю:
Теперь находим модули отклонений от средней:
…
и так далее до:
Вычисления удобно проводить на калькуляторе или в Экселе, а результаты заносить в таблицу:
На завершающем этапе рассчитываем сумму модулей:
и среднее линейное отклонение:
ед. – оно означает, что измеренные значения в среднем отличаются от примерно на 0,6 ед.
Но помимо этого, для оценки рассеяния вариант относительно средней существует более совершенный и распространённый подход. Он состоит в том, чтобы использовать не модули, а возведение отклонений в квадрат: (чтобы ликвидировать встречающиеся отрицательные значения).
Генеральная и выборочная дисперсия
Дисперсия с латыни так и переводится – рассеяние.
…не сломать бы язык 🙂 …так… Выборочная дисперсия – это среднее арифметическое квадратов отклонений всех вариант выборки от её средней:
– для несгруппированных данных, и:
– для сформированного вариационного ряда, где – кратные (одинаковые по значению) варианты в дискретном случае либо середины частичных интервалов– в интервальном, и – соответствующие частоты.
Еще раз не спеша и ОСМЫСЛЕННО прочитайте определение и выполните
Задание:
Сформулировать и записать (на бумагу!) определение генеральной дисперсии и соответствующие формулы.
Свериться можно, как обычно, в конце урока.
После чего следует
продолжение Примера 13
По тем же исходным данным вычислить выборочную дисперсию
Без проблем. Вместо модулей рассчитываем квадраты отклонений:
заполняем табличку:
и порядок:
квадратных (!) единиц – коль скоро, мы возводили в квадрат. И, чтобы вернуться в размерность задачи, из дисперсии следует извлечь корень. Но мы не будем торопить события, лучше посмотрим, как выполнять вычисления в Экселе:
Ответ:
Разобранная задача де-факто встречается в лабораторных работах по физике (да и не только) – когда некоторая величина замеряется раз 10 и затем рассчитывается среднее значение.
А теперь представьте, что вся ваша группа выполняет лабу по физике, и каждый провёл по 10 испытаний в схожих условиях. Очевидно, что у всех получились несколько разные выборочные значения , но все они без какой-либо закономерности (в общем случае) будут варьироваться вокруг истинного значения показателя (роль генеральной средней может играть некий теоретический эталон). Это свойство (отсутствие закономерности) называется несмещённостью оценки генеральной средней, и справедливо оно, как мы увидим ниже, не для всех показателей.
Теперь пару ласковых об отклонениях. В чём их смысл? Всё просто: у кого эти показатели ниже, тот качественнее проводит опыты (плавнее выполняет действия, точнее снимает показания с приборов, засекает время и т.п.). В идеале эти отклонения равны нулю, но это только в идеале – сам эмпиризм ситуации порождает генеральное линейное отклонение и генеральную дисперсию, которые обусловлены человеческим фактором, погрешностью приборов и так далее – вплоть до магнитных бурь.
В случае с полученными линейными отклонениями – всё то же самое, они будут безо всякой закономерности варьироваться вокруг генерального значения . Но вот с дисперсией всё не так. Полученные значения выборочной дисперсии будут давать систематически заниженную оценку генеральной дисперсии . И поэтому выборочную дисперсию следует «поправить» по формуле:
– желающие могут найти обоснование этого факта и этой формулы в специализированной литературе по математической статистике.
Показатель так и называется – исправленная выборочная дисперсия, и вот она уже является несмещённой оценкой генеральной дисперсии.
Таким образом, каждый студент должен поправить свою дисперсию, в частности, для Примера 13:
Следует отметить, что для большой выборки (от 100 и даже от 30 вариант) этой поправкой можно пренебречь, так как при дробь стремится к единице и .
И иногда дисперсию можно вовсе не поправлять. Так, в разобранном примере от нас требовалось просто вычислить выборочную дисперсию и всё. А если хочется что-то додумать, то пусть этого захочет преподаватель 🙂 Но вот если дисперсия будет «участвовать» в дальнейших действиях, то, конечно, приводим её к виду .
Более того, встречаются задачи, где вообще не понятно – выборочная ли дана совокупность или генеральная, и тогда разумно проявить аккуратность и использовать обозначения без подстрочных индексов, в частности, и .
Теперь случай, когда дан готовый вариационный ряд. У меня опять есть подходящая советская задача про телефонную станцию, но я скорректирую условие в соответствии с современными реалиями:
Пример 14
В результате выборочного исследования звонков, статистик МТС получил следующие данные (за некоторый временной промежуток):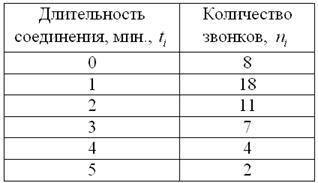
…у ОпСоСов, как известно, своя статистика – с округлением до ближайшей целой минуты :), впрочем, это тоже устареет…, как метко заметил современник, дети дружно играли во дворе – каждый в своём смартфоне(
Найти размах вариации, среднее линейное отклонение и выборочную дисперсию. Дать несмещённую оценку генеральной дисперсии и пояснить, что это означает.
Задание 7
Решить данную задачу в Экселе (данные и гайд уже там) либо на бумаге с помощью калькулятора.
Краткое решение и ответ совсем близко, поскольку 1-я часть урока подошла к концу, и я жду вас во 2-й части, где мы рассмотрим формулу для вычисления дисперсии, среднее квадратическое отклонение и коэффициент вариации.
Решения и ответы:
Задание. Генеральная дисперсия – это среднее арифметическое квадратов отклонений всех вариант генеральной совокупности от её средней:
, где – объём генеральной совокупности.
Для сформированного вариационного ряда формула принимает вид:
, где – либо варианты дискретного ряда, либо середины частичных интервалов интервального ряда, а – соответствующие частоты.
Пример 14. Решение: найдём размах вариации: мин.
Вычислим объём совокупности , произведения , их сумму и выборочную среднюю мин.
Рассчитаем , произведения и их суммы:
Среднее линейное отклонение:
мин.
Выборочная дисперсия:
мин. в квадрате.
Несмещённой оценкой генеральной дисперсии является исправленная выборочная дисперсия:
мин. в квадрате.
Несмещённость означает, что если в схожих условиях проводить аналогичные выборки, то полученные значения будут безо всякой закономерности варьироваться вокруг генерального значения .
Ответ:
Автор: Емелин Александр


Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
 Профессиональная помощь по любому предмету – Zaochnik.com
Профессиональная помощь по любому предмету – Zaochnik.com
19. Выборочная
средняя, её свойства.
Вы́борочное
(эмпири́ческое) сре́днее —
это приближение теоретического среднего
распределения, основанное на выборке
из него.
Определение:
Пусть ![]() —выборкаизраспределения
—выборкаизраспределения
вероятности, определённая на
некоторомвероятностном
пространстве![]() .
.
Тогда её выборочным средним
называетсяслучайная
величина.![]()
Свойства
выборочного среднего :
Пусть ![]() —выборочная
—выборочная
функция распределенияданной
выборки. Тогда для любого
фиксированного![]() функция
функция![]() является
является
(неслучайной)функциейдискретного
распределения. Тогдаматематическое
ожиданиеэтого распределения
равно![]()
Выборочное
среднее — несмещённая
оценкатеоретического среднего:
![]() .
.
Выборочное
среднее — сильно
состоятельная оценкатеоретического
среднего:
![]() почти
почти
наверноепри![]() .
.
Выборочное
среднее — асимптотически
нормальная оценка. Пустьдисперсияслучайных
величин![]() конечна
конечна
и ненулевая, то есть![]() .
.
Тогда
![]() по
по
распределениюпри![]() ,
,
где ![]() —нормальное
—нормальное
распределениесо средним![]() и
и
дисперсией![]() .
.
Выборочное
среднее из нормальной выборки — эффективная
оценкаеё среднего
Выборочная
дисперсия в математической
статистике —
это оценка теоретической дисперсии
распределения на основе выборки.
Различают выборочную дисперсию и
несмещённую, или исправленную, выборочные
дисперсии.
Определения
Пусть ![]() —выборкаизраспределения
—выборкаизраспределения
вероятности. Тогда
Выборочная
дисперсия — это случайная
величина
![]() ,
,
где
символ ![]() обозначаетвыборочное
обозначаетвыборочное
среднее.
Несмещённая
(исправленная) дисперсия — это случайная
величина
![]() .
.
Замечание
Очевидно,
![]() .
.
Свойства
выборочных дисперсий
Выборочная
дисперсия является
теоретической дисперсиейвыборочного
распределения. Более точно,
пусть![]() —выборочная
—выборочная
функция распределенияданной
выборки. Тогда для любого
фиксированного![]() функция
функция![]() является
является
(неслучайной)функциейдискретного
распределения. Дисперсия этого
распределения равна![]() .
.
Обе
выборочные дисперсии являются состоятельными
оценкамитеоретической дисперсии.
Если![]() ,
,
то
![]() И
И![]() ,
,
где ![]() обозначаетсходимость
обозначаетсходимость
по вероятности.
Выборочная
дисперсия является смещённой
оценкойтеоретической дисперсии,
а исправленная выборочная дисперсия
несмещённой:
![]() ,
,
И
![]() .
.
Выборочная
дисперсия нормального
распределенияимеетраспределение
хи-квадрат. Пусть![]() .
.
Тогда
![]()
21. Статистические оценки: несмещенные, эффективные, состоятельные
Состоятельной
называют такую точечную статистическую
оценку, которая при n стрем к бесконечн
стремится по вероятности к оцениваемому
параметру. В частности, если дисперсия
несмещенной оценки при n стр к беск
стремится к нулю, то такая оценка
оказывается и состоятельной.
Рассмотрим
оценку θn числового
параметра θ, определенную при n =
1, 2, … Оценка θnназывается состоятельной,
если она сходится по вероятности к
значению оцениваемого параметра θ при
безграничном возрастании объема выборки.
Выразим сказанное более подробно.
Статистика θn является
состоятельной оценкой параметра θ тогда
и только тогда, когда для любого
положительного числа ε справедливо
предельное соотношение
![]()
Пример
3. Из
закона больших чисел следует, что
θn = ![]() является
является
состоятельной оценкой θ = М(Х) (в
приведенной выше теореме Чебышёва
предполагалось существование
дисперсии D(X); однако,
как доказал А.Я. Хинчин [6], достаточно
выполнения более слабого условия –
существования математического
ожидания М(Х)).
Пример
4. Все
указанные выше оценки параметров
нормального распределения являются
состоятельными.
Вообще,
все (за редчайшими исключениями) оценки
параметров, используемые в
вероятностно-статистических методах
принятия решений, являются состоятельными.
Пример
5.
Так, согласно теореме В.И. Гливенко,
эмпирическая функция распределенияFn(x) является
состоятельной оценкой функции
распределения результатов наблюденийF(x)
Несмещенной
называют такую точечную статистическую
оценку Q*математическое
ожидание которой равно оцениваемому
параметру: M(Q*)=Q
Второе
важное свойство оценок – несмещенность.
Несмещенная оценка θn –
это оценка параметра θ, математическое
ожидание которой равно значению
оцениваемого параметра: М(θn)
= θ.
Пример
6. Из
приведенных выше результатов следует,
что ![]() и
и ![]() являются
являются
несмещенными оценками
параметров m и σ2 нормального
распределения. Поскольку М(![]() )
)
= М(m**)
= m,
то выборочная медиана ![]() и
и
полусумма крайних членов вариационного
ряда m** —
также несмещенные оценки математического
ожидания mнормального
распределения. Однако
![]()
поэтому
оценки s2 и
(σ2)**
не являются состоятельными оценками
дисперсии σ2нормального
распределения.
Оценки,
для которых соотношение М(θn)
= θ неверно, называются смещенными. При
этом разность между математическим
ожиданием оценки θn и
оцениваемым параметром θ, т.е. М(θn)
– θ, называется смещением оценки.
Пример
7. Для
оценки s2,
как следует из сказанного выше, смещение
равно
М(s2)
— σ2 =
— σ2/n.
Смещение
оценки s2 стремится
к 0 при n →
∞.
Оценка,
для которой смещение стремится к 0, когда
объем выборки стремится к бесконечности,
называется асимптотически
несмещенной.
В примере 7 показано, что оценка s2 является
асимптотически несмещенной.
Практически
все оценки параметров, используемые в
вероятностно-статистических методах
принятия решений, являются либо
несмещенными, либо асимптотически
несмещенными. Для несмещенных оценок
показателем точности оценки служит
дисперсия – чем дисперсия меньше, тем
оценка лучше. Для смещенных оценок
показателем точности служит математическое
ожидание квадрата оценки М(θn –
θ)2.
Как следует из основных свойств
математического ожидания и дисперсии,
![]()
(3)
т.е.
математическое ожидание квадрата ошибки
складывается из дисперсии оценки и
квадрата ее смещения.
Для
подавляющего большинства оценок
параметров, используемых в
вероятностно-статистических методах
принятия решений, дисперсия имеет
порядок 1/n,
а смещение – не более чем 1/n,
где n –
объем выборки. Для таких оценок при
больших n второе
слагаемое в правой части (3) пренебрежимо
мало по сравнению с первым, и для них
справедливо приближенное равенство
![]()
(4)
где с –
число, определяемое методом вычисления
оценок θn и
истинным значением оцениваемого
параметра θ.
Эффективной
называют такую точечную статистическую
оценку, которая при фиксированном n
имеет наименьшую дисперсию.
С
дисперсией оценки связано третье важное
свойство метода оценивания –эффективность.
Эффективная оценка – это несмещенная
оценка, имеющая наименьшую дисперсию
из всех возможных несмещенных оценок
данного параметра.
Доказано
[11], что ![]() и
и ![]() являются
являются
эффективными оценками
параметров m и σ2нормального
распределения. В то же время для выборочной
медианы ![]() справедливо
справедливо
предельное соотношение
![]()
Другими
словами, эффективность выборочной
медианы, т.е. отношение дисперсии
эффективной оценки ![]() параметра m к
параметра m к
дисперсии несмещенной оценки ![]() этого
этого
параметра при больших n близка к 0,637.
Именно из-за сравнительно низкой
эффективности выборочной медианы в
качестве оценки математического ожидания
нормального распределения обычно
используют выборочное среднее
арифметическое.
Понятие
эффективности вводится для несмещенных
оценок, для которых М(θn)
= θ для всех возможных значений параметра
θ. Если не требовать несмещенности, то
можно указать оценки, при некоторых θ
имеющие меньшую дисперсию и средний
квадрат ошибки, чем эффективные.
Пример
8. Рассмотрим
«оценку» математического ожидания m1 ≡
0. Тогда D(m1) =
0, т.е. всегда меньше дисперсии D(![]() )
)
эффективной оценки ![]() .
.
Математическое ожидание среднего
квадрата ошибки dn(m1)
= m2,
т.е. при ![]() имеем dn(m1)
имеем dn(m1)
< dn(![]() ).
).
Ясно, однако, что статистику m1 ≡
0 бессмысленно рассматривать в качестве
оценки математического ожидания m.
Пример
9. Более
интересный пример рассмотрен американским
математиком Дж. Ходжесом:
![]()
Ясно,
что Tn –
состоятельная, асимптотически несмещенная
оценка математического ожидания m,
при этом, как нетрудно вычислить,
![]()
Последняя
формула показывает, что при m ≠
0 оценка Tn не
хуже ![]() (при
(при
сравнении по среднему квадрату ошибки dn),
а при m =
0 – в четыре раза лучше.
Подавляющее
большинство оценок θn,
используемых в вероятностно-статистических
методах, являются асимптотически
нормальными, т.е. для них справедливы
предельные соотношения:
![]()
для
любого х,
где Ф(х) –
функция стандартного нормального
распределения с математическим ожиданием
0 и дисперсией 1. Это означает, что для
больших объемов выборок (практически
— несколько десятков или сотен наблюдений)
распределения оценок полностью
описываются их математическими ожиданиями
и дисперсиями, а качество оценок –
значениями средних квадратов ошибок dn(θn).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
