Каким свойством пространства обуславливается справедливость закона сохранения импульса

В предыдущих разделах рассмотрены три фундаментальных закона природы: закон сохранения импульса, момента импульса и энергии. Следует
понимать, что эти законы выполняются только в инерциальных системах отсчета.
В самом деле, при выводе этих законов мы пользовались вторым и третьим законами Ньютона, а они применимы только в инерциальных
системах. Напомним также, что импульс и момент импульса сохраняются в том случае, если система замкнутая (сумма всех внешних сил и
всех моментов сил равна нулю). Для сохранения же энергии тела условия замкнутости недостаточно – тело должно быть еще и адиабатически
изолированным (т.е. не участвовать в теплообмене).
Во всей истории развития физики законы сохранения оказались чуть ли не единственными законами, сохранившими свое значение при
замене одних теорий другими. Эти законы тесно связаны с основными свойствами пространства и времени.
равнозначность всех моментов времени (симметрия по отношению к сдвигу начала отсчета времени). Равнозначность следует понимать в
том смысле, что замена момента времени t1 на момент времени t2, без изменения значений
координат и скорости частиц, не изменяет механические свойства системы. Это означает то, что после указанной замены, координаты
и скорости частиц имеют в любой момент времени t2 + t такие же значения, какие имели
до замены, в момент времени t1 + t.
одинаковость свойств пространства во всех точках (симметрия по отношению к сдвигу начала координат). Одинаковость следует понимать
в том смысле, что параллельный перенос замкнутой системы из одного места пространства в другое, без изменения взаимного расположения
и скоростей частиц, не изменяет механические свойства системы.
одинаковость свойств пространства по всем направлениям (симметрия по отношению к повороту осей координат). Одинаковость следует
понимать в том смысле, что поворот замкнутой системы, как целого, не отражается на её механических свойствах.
Между законами типа основного уравнения динамики и законами сохранения имеется принципиальная разница. Законы динамики дают нам
представление о детальном ходе процесса. Так, если задана сила, действующая на материальную точку и начальные условия, то можно
найти закон движения, траекторию, величину и направление скорости в любой момент времени и т. п. Законы же сохранения не дают
нам прямых указаний на то, как должен идти тот или иной процесс. Они говорят лишь о том, какие процессы запрещены и потому в
природе не происходят.
Таким образом, законы сохранения проявляются как принципы запрета: любое явление, при котором не выполняется хотя бы один из
законов сохранения, запрещено, и в природе такие явления никогда не наблюдаются. Всякое явление, при котором не нарушается ни
один из законов сохранения, в принципе может происходить.
Рассмотрим следующий пример. Может ли покоящееся тело за счет внутренней энергии начать двигаться? Этот процесс не противоречит
закону сохранения энергии. Нужно лишь, чтобы возникающая кинетическая энергия точно равнялась убыли внутренней энергии.
На самом деле такой процесс никогда не происходит, ибо он противоречит закону сохранения импульса. Раз тело покоилось, то его
импульс был равен нулю. А если оно станет двигаться, то его импульс сам собой увеличится, что невозможно. Поэтому внутренняя
энергия тела не может превратиться в кинетическую, если тело не распадётся на части.
Если же допустить возможность распада этого тела на части, то запрет, налагаемый законом сохранения импульса, снимается. При этом
возникшие осколки могут двигаться так, чтобы их центр масс оставался в покое, – а только этого и требует закон сохранения импульса.
Итак, для того чтобы внутренняя энергия покоящегося тела могла превратиться в кинетическую, это тело должно распасться на части.
Если же есть еще один какой-либо закон, запрещающий распад этого тела на части, то его внутренняя энергия и масса покоя будут
постоянными величинами.
Фундаментальность законов сохранения заключается в их универсальности. Они справедливы при изучении любых физических
процессов (механических, тепловых, электромагнитных и др.). Они одинаково применимы в релятивистском и нерелятивистском движении,
в микромире, где справедливы квантовые представления, и в макромире, с его классическими представлениями.
Физика, 10 класс
Урок 11.Импульс. Закон сохранения импульса
Перечень вопросов, рассматриваемых на уроке:
1) импульс тела, импульс силы, замкнутая система;
2) абсолютно упругий, абсолютно неупругий удар;
3) закон сохранения импульса;
4) границы применимости закона;
5) проявление закона сохранения импульса в технике и природе.
Глоссарий по теме
Импульс тела (материальной точки) — векторная величина, равная произведению массы тела на скорость тела.
Импульс силы — произведение силы на время её действия.
Импульс тела равен сумме импульсов отдельных его элементов.
Импульс системы тел равен векторной сумме импульсов каждого из тел системы.
Внутренние силы — это силы, с которыми взаимодействуют тела системы между собой.
Внешние силы — это силы, создаваемые телами, которые не принадлежат к данной системе.
Замкнутая система — это система, в которой внешние силы не действуют или сумма внешних сил равна нулю.
Абсолютно неупругий удар — это столкновение двух тел, которые объединяются и движутся дальше как одно целое.
Абсолютно упругий удар — столкновение тел, при котором тела не соединяются и их внутренние энергии остаются неизменными.
Закон сохранения импульса: векторная сумма импульсов тел, образующих замкнутую систему, не меняется при любых взаимодействиях между телами системы.
Основная и дополнительная литература по теме урока:
Г.Я. Мякишев., Б.Б.Буховцев., Н.Н.Сотский. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 123 – 130.
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.
Открытые электронные ресурсы:
https://kvant.mccme.ru/1979/10/zakon_sohraneniya_impulsa_reak.htm
Основное содержание урока
Импульс тела (материальной точки) представляет собой векторную величину, равную произведению массы тела на скорость тела:

Направление импульса всегда совпадает с направлением скорости, так как m > 0, то

Любое движущееся тела имеет импульс.
Единица измерения импульса:
 .
.
Произведение силы на время её действия называется импульсом силы.

Второй закон Ньютона в импульсной форме.
Изменение импульса тела (материальной точки) равно импульсу действующей на него силы:

Импульс тела равен сумме импульсов отдельных его элементов:

Импульс системы тела равен векторной сумме импульсов каждого из тел системы:

Импульс обладает интересным свойством сохраняться, которое есть только у нескольких физических величинах.
Силы, с которыми взаимодействуют тела системы друг с другом, называются внутренними, а силы, создаваемые телами, которые не принадлежат этой системе, являются внешними силами.
Система, в которой внешние силы не действуют или сумма внешних сил равна нулю, называется замкнутой.
Полный импульс тел сохраняется, в замкнутой системе тела могут только обмениваться импульсами.
Столкновение тел представляет собой взаимодействие тел при их относительном перемещении. Абсолютно неупругий удар — это столкновение двух тел, которые объединяются и движутся дальше как одно целое.
Закон сохранения импульса при неупругом ударе:

Абсолютно упругий удар — столкновение тел, при котором тела не соединяются в одно целое и их внутренние энергии остаются неизменными.
Закон сохранения импульса при упругом ударе:

Закон сохранения импульса.
Если внешние силы на систему не действуют или их сумма равна нулю, то импульс системы остается неизменным:

Закон сохранения импульса является одним из основных законов физики.
Границы применимости закона сохранения импульса: замкнутая система.
Закон сохранения импульса с честью выдержал испытание временем и до сих пор он продолжает свое триумфальное шествие.
Он дал неоценимый инструмент для исследования ученым, как один из фундаментальных законов физики, ставя запрет одним процессам и открывая дорогу другим.
Действие этого закона проявляется в науке, в технике, в природе и в повседневной жизни. Всюду этот закон работает отлично — реактивное движение, атомные и ядерные превращения, взрыв и т.д.
Во многих повседневных ситуациях помогает разобраться понятие импульса.
Рене Декарт попытался использовать термин «импульс» вместо силы. Это связано с тем, что силу трудно измерить, а массу и скорость измерить несложно. Поэтому вместо импульса часто говорят количество движения (Именно Ньютон первым назвал произведение массы тела на скорость количеством движения).
Декарт понимал большое значение понятия количества движения — или импульса тела — как произведения массы тела на скорость. Но он совершил ошибку, не рассматривая количество движения как векторную величину. Ошибка эта была исправлена в начале XVIII века.
Используя закон сохранения импульса можно «найти» и невидимые объекты, например, электромагнитные волны, излучаемые открытым колебательным контуром, или антинейтрино – субатомные частицы, не оставляющие следов в детекторах.
Разбор тренировочных заданий
1. Тело свободно падает без начальной скорости. Изменение модуля импульса этого тела за промежуток времени 2 с равно 10 кг∙м/с. Чему равна масса тела?
Дано: ∆t =???? c; g ≈ ????0 м∕с2; ∆р =????0 кг∙м ∕с.
Найти: m.
Решение:
 т.к. тело свободно падает.
т.к. тело свободно падает.
Запишем второй закон Ньютона в импульсной форме:
∆р = F∆t,
F = mg – т.к. при свободном падении действует только сила тяжести,
тогда ∆р = mg∆t, откуда:

Делаем расчёт:

Ответ: m = 0,5 кг.
2. Тело массой 400 г изменяет свои координаты по закону:

Тело будет иметь импульс 8 Н·с после начала движения за промежуток времени равный __________?
Дано:

m = 400 г = 0,4 кг; p = 8 Н∙с
Найти: t.
Решение:
Записываем формулу импульса:
p = mv,
скорость равна 1-й производной от х по времени:
v = x'(t)= 4 + 4t
Из 1-й формулы скорость равна: v = p/m
4 + 4t = 8 / 0,4,
4t = 20 − 4 = 16,
t = 16 / 4,
t = 4 с.
Ответ: t = 4 с.
Закон сохранения импульса
Закон сохранения импульса можно наблюдать повсюду. Он достаточно точно выполняется в реальных условиях, если пренебречь сопротивлением воздуха, силами трения и т.д. Примеры проявления этого закона:
- стрелок ощущает отдачу при выстреле из ружья;
- рыбак переходит с кормы на нос лодки, а лодка при этом движется в противоположную сторону;
- шары сталкиваются на бильярдном столе.
Однако, прежде чем говорить о законе сохранении импульса, рассмотрим понятие замкнутой системы.
Замкнутая система — система тел, на которую со стороны других тел не действуют внешние силы.
Формулировка закона сохранения импульса (ЗСИ)
Векторная сумма импульсов всех тел, входящих в замкнутую систему, остается постоянной при любых взаимодействиях этих тел между собой внутри системы.
Данный закон является следствием из второго и третьего законов Ньютона. Покажем это.
Возьмем замкнутую систему из двух взаимодействующих тел. Силы F1→ и F2→ — это силы взаимодействия между телами. Третий закон Ньютона гласит, что F2→=-F1→. Пусть тела взаимодействуют во течение времени t. Тогда импульсы сил одинаковы по модулю и противоположны по направлению, как и сами силы.
F2t→=-F1→t.
По второму закону Ньютона:
F1→t=m1v1’→-m1v1→; F2→t=m1v2’→-m1v2→
Здесь v1’→ и v2’→ — скорости тел в конце взаимодействия. Соответственно, скорости без штрихов обозначают эти величины в начальный момент взаимодействия.
Из записанного выше следует соотношение:
m1v1→+m2v2→=m1v1’→+m2v2’→
Это равенство — математическая форма записи закона сохранения импульса. Оно означает, что суммарный импульс системы в результате какого-то взаимодействия не изменился.
Проиллюстрируем закон сохранения импульса на примере соударения шаров разных масс. Один из шаров до удара покоился.
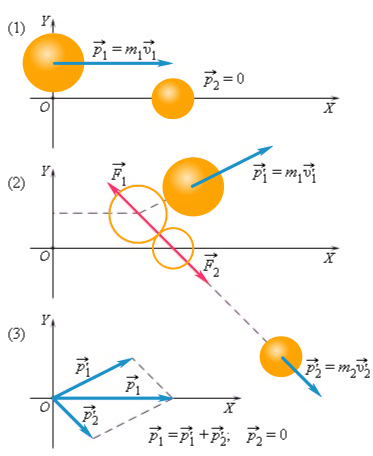
Как видим, после удара векторная сумма импульсов двух шаров равна первоначальному импульсу движущегося шара.
Важно! Закон сохранения выполняется и для проекций векторов на координатные оси.
Закон сохранения импульса позволяет решать задачи и находить скорости тел не зная значений действующих сил.
Рассмотрим снаряд, вылетающий из пушки.
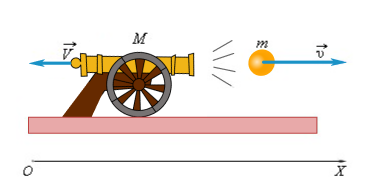
В данном случае взаимодействующие тела — это снаряд и пушка. Сначала тела не движутся. При выстреле снаряд приобретает скорость v→ и летит вперед, а пушка откатывается назад со скоростью V→. Откатывание пушки называется отдачей от выстрела.
По закону сохранения импульса в проекции на ось OX можно записать:
mv-MV=0
V=mvM.
Реактивное движение
Реактивное движение также основано на принципе отдачи. Нагретые газы выбрасываются из сопла реактивного двигателя со скоростью u→. Пусть масса газов равна m, а масса ракеты после истечения газов — M. Рассматривая замкнутую систему «ракета-газы» и применяя к ней закон сохранения импульса, можно вычислить скорость ракеты V после истечения газов.
V=muM
Формула для пушки и снаряда не применима к ракете, так как дает лишь приблизительное представление о движении ракеты, На самом деле вся масса газов выходит из сопла не сразу, а постепенно.
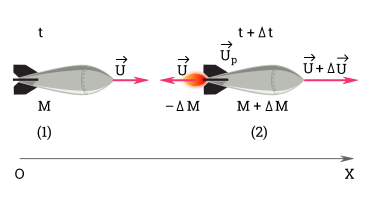
Рассмотрим этот процесс подробнее. Пусть масса ракеты в момент времени t равна M, а сама ракета движется со скоростью v→. В течение малого промежутка времени ∆t из сопла ракеты выбрасывается порция газа с относительной скоростью u→. По истечении времени ∆t ракета будет двигаться со скоростью v+∆v, а масса ракеты станет равной M-∆M.
В момент t+∆t импульс ракеты равен:
M-∆M·v→+∆v→.
Импульс реактивных газов:
∆M·v→+u→.
По закону сохранения импульса:
Mv→=M-∆M·v→+∆v→+∆M·v→+u→.
Или
M∆v→=∆M·u→-∆M·∆v→.
Величиной ∆M·∆v→ можно пренебречь, так как ∆M намного меньше M.
Разделим последнее равенство на ∆t и перейдем к пределу ∆t→0.
M∆v→∆t=∆M·u→∆t (∆t→0)
Ma→=-μu→.
Здесь μ — расход топлива в единицу времени, а -μu→ — реактивная сила тяги. Направление этой силы совпадает с направлением движения ракеты.
Формула Ma→=-μu→ выражает второй закон Ньютона для тела переменной массы. В скалярном виде ее можно переписать так:
Ma=μu.
Конечная скорость ракеты определяется по формуле:
v=ulnM0M.
Это так называемая формула Циолковского, согласно которой конечная скорость ракеты может превышать скорость истечения газов из сопла двигателя. Правда, достижение такой скорости связано с определенными сложностями. Во-первых такими, как значительный расход топлива.
Для того, чтобы развить первую космическую скорость v=v1=7,9·103 мс при скорости истечения газов u=3·103 мс стартовая масса ракеты должна быть примерно в 14 раз больше конечной массы.
Современное ракетостроение развивается в направлении экономичных многоступенчатых ракет. Сброс отсеков с отработанным топливом позволяет значительно сократить массу ракеты и оптимизировать дальнейший расход топлива для ее разгона.
Рассмотрим изменение импульсов тел при их взаимодействии друг с другом.
Если два или несколько тел взаимодействуют только между собой (то есть не подвергаются воздействию внешних сил), то эти тела образуют замкнутую систему.
Импульс, равный векторной сумме импульсов тел, входящих в замкнутую систему, называется суммарным импульсом этой системы.
Таким образом, чтобы найти суммарный импульс замкнутой системы (n) тел, необходимо найти векторную сумму импульсов всех тел, входящих в данную систему:
pсум→=p1→+p2→+…+pn→.
Импульс каждого из тел, входящих в замкнутую систему, может меняться в результате их взаимодействия друг с другом.
Векторная сумма импульсов тел, составляющих замкнутую систему, не меняется с течением времени при любых движениях и взаимодействиях этих тел.
В этом заключается закон сохранения импульса, который называют также законом сохранения количества движения.
Закон сохранения импульса впервые был сформулирован Р. Декартом. В одном из своих писем он написал:
«Я принимаю, что во Вселенной, во всей созданной материи есть известное количество движения, которое никогда не увеличивается, не уменьшается, и, таким образом, если одно тело приводит в движение другое, то теряет столько своего движения, сколько его сообщает».
Рассмотрим систему, состоящую только из двух тел — шаров массами m1 и m2, которые движутся прямолинейно навстречу друг другу со скоростями v1 и v2. Шары обладают импульсами p1→=m1v1→ и p2→=m2v2→ соответственно.
Через некоторое время шары столкнутся. Во время столкновения, длящегося в течение очень короткого промежутка времени (t), возникнут силы взаимодействия F1→ и F2→, приложенные соответственно к первому и второму шару. В результате действия этих сил скорости шаров изменятся. Обозначим скорости шаров после соударения v1′ и v2′. И импульсы шаров станут p1→′=m1v1→′ и p2→′=m2v2→′ соответственно.
Тогда, согласно закону сохранения импульса, имеют место равенства:
или
m1v1→+m2v2→=m1v1→′+m2v2→′.
Данные равенства являются математической записью закона сохранения импульса.
Закон сохранения импульса выполняется и в том случае, если на тела системы действуют внешние силы, векторная сумма которых равна нулю.
Таким образом, более точно закон сохранения импульса формулируется так:
векторная сумма импульсов всех тел замкнутой системы — величина постоянная, если внешние силы, действующие на неё, отсутствуют, или же их векторная сумма равна нулю.
Импульс системы тел может измениться только в результате действия на систему внешних сил. И тогда закон сохранения импульса действовать не будет.
Пример:
при стрельбе из пушки возникает отдача: снаряд летит вперёд, а само орудие откатывается назад. Почему?
Снаряд и пушка — замкнутая система, в которой действует закон сохранения импульса. В результате выстрела из пушки импульс самой пушки и импульс снаряда изменятся. Но сумма импульсов пушки и находящегося в ней снаряда до выстрела останется равной сумме импульсов откатывающейся пушки и летящего снаряда после выстрела.
Обрати внимание!
В природе замкнутых систем не существует. Но если время действия внешних сил очень мало, например, во время взрыва, выстрела и т. п., то в этом случае воздействием внешних сил на систему пренебрегают, а саму систему рассматривают как замкнутую.
Кроме того, если на систему действуют внешние силы, но сумма их проекций на одну из координатных осей равна нулю (то есть силы уравновешены в направлении этой оси), то в этом направлении закон сохранения импульса выполняется.
Великий учёный Исаак Ньютон изобрёл наглядную демонстрацию закона сохранения импульса — маятник, или её ещё называют «колыбель». Это устройство представляет собой конструкцию из пяти одинаковых металлических шаров, каждый из которых крепится с помощью двух тросов к каркасу, а тот в свою очередь — к прочному основанию П-образной формы.
Маятник Ньютона устроен так, что начальный шар передаёт импульс второму шарику, а затем замирает. Нашему глазу на первый взгляд не заметно, как следующий шарик принимает импульс от предыдущего, мы не можем проследить его скорость. Но, если взглянуть пристальнее, можно заметить, как шарик немножко «вздрагивает». Это объясняется тем, что он совершает движения с посланной ему скоростью, но поскольку расстояние очень маленькое, ему некуда разогнаться, то он может на своём коротком пути передать импульс третьему шарику и в итоге остановиться.
Такое же действие совершает и следующий шарик и т. д. Последнему шарику некуда передавать свой импульс, поэтому он свободно колеблется, поднимаясь на определённую высоту, а затем возвращается, и весь процесс передачи импульсов повторяется в обратном порядке.
Самый яркий пример применения закона сохранения импульса — реактивное движение.
Источники:
Пёрышкин А. В., Гутник Е. М. Физика, 9 кл.: учебник. — М.: Дрофа, 2014. — 319 с.
www.klassnoedelo.ru, сайт «Классное дело — новые технологии в образовании»
www.barvinok80.narod.ru, сайт дошкольного учреждения образования «Барвинок»
www.hottabich.com.ua, сайт «Hottabich»
www.thegreenhead.com, сайт «Green Head»
www.askskb.net, сайт «Интерактивная физика»
