Каким свойством обладают углы равнобедренные треугольники

Равнобедренный треугольник, свойства, признаки и формулы
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой по длине.
Равнобедренный треугольник (понятие)
Свойства равнобедренного треугольника
Признаки равнобедренного треугольника
Формулы равнобедренного треугольника
Остроугольный треугольник, прямоугольный треугольник, равнобедренный треугольник, равносторонний треугольник, тупоугольный треугольник
Равнобедренный треугольник (понятие):
Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой по длине.
Две равные стороны равнобедренного треугольника называются боковыми, а третья неравная им сторона – основанием.

Рис. 1. Равнобедренный треугольник
АВ = ВС – боковые стороны, АС – основание,
∠ АВС – вершинный угол, ∠ BАC и ∠ BСA – углы при основании
По определению, каждый правильный (равносторонний) треугольник также является равнобедренным, но не каждый равнобедренный треугольник – правильным (равносторонним).
Угол, образованный боковыми сторонами, называется вершинным углом, а углы, одной из сторон которых является основание, называются углами при основании.
Различают следующие виды равнобедренных треугольников:
– остроугольный – все углы острые;
– прямоугольный – угол при вершине прямой, а при основании углы острые;
– тупоугольный – угол при вершине тупой, а при основании углы острые;
– равносторонний (или правильный) – все стороны равны и все углы равны.
Свойства равнобедренного треугольника:
1. В равнобедренном треугольнике углы при основании равны.

Рис. 2. Равнобедренный треугольник
∠ BАC = ∠ BСA
2. Биссектрисы, медианы и высоты, проведённые из этих углов равны между собой.

Рис. 3. Равнобедренный треугольник
АН1 = СН2 – высота, АМ1 = СМ2 – медиана, АL1 = СL2 – биссектриса, проведённые из углов при основании
3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Рис. 4. Равнобедренный треугольник
ВD – биссектриса, высота и медиана, проведенные к основанию – это один и тот же отрезок
4. Центры вписанной и описанной окружностей лежат на медиане (биссектрисе, высоте), проведенной к основанию равнобедренного треугольника.

Рис. 5. Равнобедренный треугольник
R – радиус описанной окружности, r – радиус вписанной окружности
Признаки равнобедренного треугольника:
– если в треугольнике два угла равны, то он равнобедренный;
– если в треугольнике биссектриса является медианой или высотой, то этот треугольник равнобедренный;
– если в треугольнике медиана является биссектрисой или высотой, то этот треугольник равнобедренный;
– если в треугольнике высота является медианой или биссектрисой, то этот треугольник равнобедренный.
Формулы равнобедренного треугольника:
Пусть a – длина двух равных сторон равнобедренного треугольника, b – длина основания, h – высота (биссектриса, медиана) равнобедренного треугольника, проведенная к основанию, α – углы при основании, β – вершинный угол, R – радиус описанной окружности, r – радиус вписанной окружности (см. Рис. 6, 7, 8).

Рис. 6. Равнобедренный треугольник
Формулы длины основания (b):
![]() ,
,
![]() ,
,
![]() .
.
Формулы длины равных сторон (а):
![]() .
.
Формулы углов:

Рис. 7. Равнобедренный треугольник
![]() ,
,
![]() ,
,
 .
.
Формулы периметра (Р) равнобедренного треугольника:

Рис. 8. Равнобедренный треугольник
![]() ,
,
![]() .
.
Формулы площади (S) равнобедренного треугольника:
 ,
,
 ,
,
 .
.
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
карта сайта
Коэффициент востребованности
2 523
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Среди всех треугольников есть два особенных вида: прямоугольные треугольники и равнобедренные треугольники. Чем же эти виды треугольников такие уж особенные? Ну, во-первых, такие треугольники чрезвычайно часто оказываются главными действующими «лицами» задач ЕГЭ первой части. А во-вторых, задачи про прямоугольные и равнобедренные треугольники решаются гораздо легче, чем другие задачи по геометрии. Нужно всего лишь знать несколько правил и свойств. Все самое интересное о прямоугольных треугольниках обсуждается в соответствующей теме, а сейчас рассмотрим равнобедренные треугольники. И прежде всего, что же такое – равнобедренный треугольник. Или, как говорят математики, каково определение равнобедренного треугольника?
Треугольник называется равнобедренным, если у него есть две равные стороны.
Посмотри, как это выглядит:

Как и у прямоугольного треугольника, у равнобедренного треугольника есть специальные названия для сторон. Две равные стороны называются боковыми сторонами, а третья сторона – основанием.
И снова внимание на картинку:

Может быть, конечно, и так:

Так что будь внимательным: боковая сторона – одна из двух равных сторон в равнобедренном треугольнике, а основание – третья сторона.
Чем же так уж хорош равнобедренный треугольник? Чтобы это понять, давай проведём высоту к основанию. Ты помнишь, что такое высота?
 | Это просто линия, проведённая из вершины треугольника перпендикулярно противоположной стороне. Итак, провели высоту. |
Что же получилось? Из одного равнобедренного треугольника получилось два прямоугольных.
Это уже хорошо, но так получится в любом, самом «кособедренном» треугольнике.
Смотри:
 | Тоже два прямоугольных…. |
Чем же отличается картинка для равнобедренного треугольника? Смотри ещё раз:
 | Видишь, два прямоугольных треугольника ( и ) – одинаковые! Или, как математически любят говорить? равные! |
Ну, во-первых, конечно, этим странным математикам мало просто видеть – нужно непременно доказывать. А то вдруг эти треугольники чуть-чуть разные, а мы будем считать их одинаковыми.
Но не переживай: в данном случае доказывать почти так же просто, как и видеть.
Начнём? Посмотри внимательно, у нас есть:
 | (ещё говорят, — общая) |
И, значит, ! Почему? Да мы просто найдём и , и из теоремы Пифагора (помня ещё при этом, что )
Удостоверились? Ну вот, теперь у нас
А уж по трём сторонам – самый легкий (третий) признак равенства треугольников.
Ну вот, наш равнобедренный треугольник разделился на два одинаковых прямоугольных.
 | Отметим на картинке все одинаковые элементы (углы и стороны). |
Видишь, как интересно? Получилось, что:
Как же об этом принято говорить у математиков? Давай по порядку:
- В равнобедренном треугольнике углы при основании равны
- Высота, проведенная к основанию, совпадает с медианой и биссектрисой.
(Вспоминаем тут, что медиана – линия, проведённая из вершины, которая делит сторону пополам, а биссектриса – угол.)
Ну вот, здесь мы обсудили, что хорошего можно увидеть, если дан равнобедренный треугольник. Мы вывели, что у равнобедренного треугольника углы при основании равны, а высота, биссектриса и медиана, проведенные к основанию, совпадают.
И теперь возникает другой вопрос: а как узнать равнобедренный треугольник? То есть, как говорят математики, каковы признаки равнобедренного треугольника?
И оказывается, что нужно просто «перевернуть» все высказывания наоборот. Так, конечно, не всегда бывает, но равнобедренный треугольник всё-таки отличная штука! Что же получится после «переворачивания»?
I. Если в каком-то треугольнике есть два равных угла, то такой треугольник – равнобедренный (ну и естественно, углы эти окажутся при основании).

II. Если в каком-то треугольнике
- высота и медиана или
- высота и биссектриса или
- биссектриса и медиана
проведённые к какой-то стороне, совпадут, то такой треугольник – равнобедренный, а сторона эта – основание.
Ну вот смотри:
Если совпадают высота и медиана, то:

Если совпадают высота и биссектриса, то:
Если совпадают биссектриса и медиана, то:

Ну вот, не забывай и пользуйся:
- Если дан равнобедренный треугольный треугольник, смело проводи высоту, получай два прямоугольных треугольника и решай задачу уже про прямоугольный треугольник.
- Если дано, что два угла равны, то треугольник точно равнобедренный и можно проводить высоту и ….( Дом, который построил Джек…).
- Если оказалось, что высота разделена сторону пополам, то треугольник – равнобедренный со всеми вытекающими бонусами.
- Если оказалось, что высота разделила угол полам – тоже равнобедренный!
- Если биссектриса разделила сторону пополам или медиана – угол, то это тоже бывает только в равнобедренном треугольнике
Давай посмотрим, как выглядит в задачах.
Задача 1 (самая простая)
В треугольнике стороны и равны, а . Найти .
Решаем:
Сначала рисунок.

Что здесь – основание? Конечно, .
Вспоминаем, что если , то и .
Обновлённый рисунок:

Обозначим за . Чему там равна сумма углов треугольника? ?
Пользуемся:
Вот и ответ: .
Несложно, правда? Даже высоту проводить не пришлось.
Задача 2 (Тоже не очень хитрая, но нужно повторить тему «Прямоугольный треугольник»)
В треугольнике , . Найти .
Решаем:
 | Смотрим внимательно и соображаем, что раз , то . |

Треугольник-то — равнобедренный! Проводим высоту (это и есть фокус, с помощью которого сейчас все решится).
 | Вспоминаем, что высота = медиана, то есть . |
Теперь «вычёркиваем из жизни» , рассмотрим только .

Итак, в имеем:
Вспоминаем табличное значения косинусов (ну, или глядим в шпаргалку…)
Осталось найти : .
Ответ: .
Заметим, что нам тут очень потребовались знания, касающиеся прямоугольного треугольника и «табличных» синусов и косинусов. Очень часто так и бывает: темы «Прямоугольный треугольник», «Равнобедренный треугольник» и «Основные формулы тригонометрии» в задачках ходят в связках, а с другими темами не слишком дружат.
Равнобедренный треугольник. Средний уровень.
Треугольник называется равнобедренным, если у него есть две равные стороны.

Эти две равные стороны называются боковыми сторонами, а третья сторона – основание равнобедренного треугольника.
Посмотри на рисунок: и – боковые стороны, – основание равнобедренного треугольника.

Свойства равнобедренного треугольника:
- Углы при основании равнобедренного треугольника равны (на рисунке: ).
- Высота, проведённая к основанию равнобедренного треугольника, совпадает с медианой и биссектрисой.
Давай на одном рисунке поймём, почему так выходит. Проведем из точки высоту .
 | Что получилось? Треугольник разделился на два прямоугольных треугольника и . И эти треугольники равны! У них равны гипотенузы и общий катет . |
Значит, у них равны все соответствующие элементы.
То есть:
 |
|
Всё! Одним махом (высотой ) доказали сразу все утверждения.
И ты запомни: чтобы решить задачу про равнобедренный треугольник часто бывает очень полезно опустить высоту на основание равнобедренного треугольника и разделить его на два равных прямоугольных треугольника.
Признаки равнобедренного треугольника
Верны и обратные утверждения:
- Если в некотором треугольнике два угла равны, то он – равнобедренный.
- Если в некотором треугольнике совпадают:
а) высота и биссектриса или
б) высота и медиана или
в) медиана и биссектриса,
проведённые к одной стороне, то такой треугольник – равнобедренный.
Почти все из этих утверждений снова можно доказать «одним махом».
1. Итак, пусть в оказались равны и .

Проведём высоту . Тогда
 | – как прямоугольные по катету и острому углу. |
Значит, .
 | Доказали, что – равнобедренный. |
2. a) Теперь пусть в каком–то треугольнике совпадают высота и биссектриса.
 | Тогда снова по катету и острому углу. Значит, опять . |
2. б) А если совпадают высота и медиана? Все почти так же, ничуть не сложнее!
 | — по двум катетам |
2. в) А вот если нет высоты, которая опущена на основание равнобедренного треугольника, то нет и никаких изначально прямоугольных треугольников. Плохо!

Но выход есть – читай его в следующем уровне теории, поскольку тут доказательство посложнее, а пока просто запомни, что если медиана и биссектриса совпали, то треугольник тоже окажется равнобедренным, и высота всё-таки тоже совпадёт с этими биссектрисой и медианой.
Подытожим:
- Если треугольник равнобедренный, то углы при основании равны, и высота, биссектриса и медиана, проведенные к основанию, совпадают.
- Если в каком-то треугольнике найдутся два равных угла, или какие-то две из трех линий (биссектриса, медиана, высота) совпадут, то такой треугольник – равнобедренный.
Равнобедренный треугольник. Краткое описание и основные формулы
Равнобедренный треугольник — треугольник, у которого есть две равные стороны.
 |
|
Свойства равнобедренного треугольника:
 |
|
Признаки равнобедренного треугольника:
- Если в некотором треугольнике два угла равны, то он – равнобедренный.
- Если в некотором треугольнике совпадают:
а) высота и биссектриса или
б) высота и медиана или
в) медиана и биссектриса,
проведённые к одной стороне, то такой треугольник – равнобедренный.
ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!
Стать учеником YouClever,
Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц»,
А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.
можно кликнув по этой ссылке.
Свойства равнобедренного треугольника выражают следующие теоремы.
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Теорема 3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема 4. В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Докажем одну из них, например теорему 2.5.
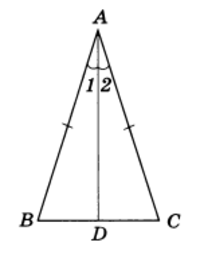
Рис.1
Доказательство. Рассмотрим равнобедренный треугольник ABC с основанием ВС и докажем, что ∠ В = ∠ С. Пусть AD — биссектриса треугольника ABC (рис.1). Треугольники ABD и ACD равны по первому признаку равенства треугольников (АВ = АС по условию, AD — общая сторона, ∠ 1 = ∠ 2, так как AD — биссектриса). Из равенства этих треугольников следует, что ∠ В = ∠ С. Теорема доказана.
С использованием теоремы 1 устанавливается следующая теорема.
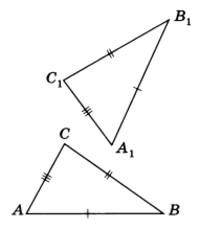
Рис.2
Теорема 5. Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны (рис. 2).
Замечание. Предложения, установленные в примерах 1 и 2, выражают свойства серединного перпендикуляра к отрезку. Из этих предложений следует, что серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Пример 1. Доказать, что точка плоскости, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.
Решение. Пусть точка М равноудалена от концов отрезка АВ (рис. 3), т. е. AM = ВМ.
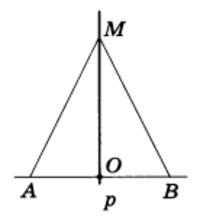
Рис.3
Тогда Δ АМВ равнобедренный. Проведем через точку М и середину О отрезка АВ прямую р. Отрезок МО по построению есть медиана равнобедренного треугольника АМВ, а следовательно (теорема 3), и высота, т. е. прямая МО, есть серединный перпендикуляр к отрезку АВ.
Пример 2. Доказать, что каждая точка серединного перпендикуляра к отрезку равноудалена от его концов.
Решение. Пусть р — серединный перпендикуляр к отрезку АВ и точка О — середина отрезка АВ (см. рис. 3).

Рис.3
Рассмотрим произвольную точку М, лежащую на прямой р. Проведем отрезки AM и ВМ. Треугольники АОМ и ВОМ равны, так как у них углы при вершине О прямые, катет ОМ общий, а катет ОА равен катету ОВ по условию. Из равенства треугольников АОМ и ВОМ следует, что AM = ВМ.
Пример 3. В треугольнике ABC (см. рис. 4) АВ = 10 см, ВС = 9 см, АС = 7 см; в треугольнике DEF DE = 7 см, EF = 10 см, FD = 9 см.
Рис.4
Сравнить треугольники ABC и DEF. Найти соответственно равные углы.
Решение. Данные треугольники равны по третьему признаку. Соответственно равные углы: А и Е (лежат против равных сторон ВС и FD), В и F (лежат против равных сторон АС и DE), С и D (лежат против равных сторон АВ и EF).
Пример 4. На рисунке 5 АВ = DC, ВС = AD, ∠B = 100°.
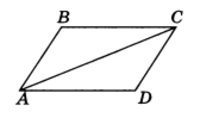
Рис.5
Найти угол D.
Решение. Рассмотрим треугольники ABC и ADC. Они равны по третьему признаку (АВ = DC, ВС = AD по условию и сторона АС — общая). Из равенства этих треугольников следует, что ∠ В = ∠ D, но угол В равен 100°, значит, и угол D равен 100°.
Пример 5. В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ABC . Ответ дайте в градусах.
Видео-решение.

| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Равнобедренный треугольник |  | Равнобедренным треугольником называют треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника. |
| Свойство | Углы при основании равнобедренного треугольника |  | Если треугольник является равнобедренным треугольником, то углы при его основании равны. |
| Признак | Два равных угла треугольника | Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. | |
| Свойство | Медиана, биссектриса и высота, проведённые к основанию равнобедренного треугольника |  | В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. |
| Признак | Высота треугольника, совпадающая с медианой |  | Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным |
| Признак | Высота треугольника, совпадающая с биссектрисой |  | Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным |
| Признак | Биссектриса треугольника, совпадающая с медианой |  | Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным |
| Определение: равнобедренный треугольник | |
 | Равнобедренным треугольником называют треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника. |
| Свойство: углы при основании равнобедренного треугольника | |
 | Если треугольник является равнобедренным треугольником, то углы при его основании равны. |
| Признак: два равных угла треугольника | |
 | Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. |
| Свойство: медиана, биссектриса и высота, проведённые к основанию равнобедренного треугольника | |
 | В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. |
| Признак: высота треугольника, совпадающая с медианой | |
 | Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным |
| Признак: высота треугольника, совпадающая с биссектрисой | |
 | Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным |
| Признак: биссектриса треугольника, совпадающая с медианой | |
 | Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным |
| Определение равнобедренного треугольника |
 Определение: Равнобедренным треугольником называют треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника. |
| Свойство углов при основании равнобедренного треугольника |
 Свойство: Если треугольник является равнобедренным треугольником, то углы при его основании равны. |
| Признак равнобедренного треуголька: два равных угла треугольника |
 Признак: Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. |
| Свойство медианы, биссектрисы и высоты, проведённых к основанию равнобедренного треугольника |
 Свойство: В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. |
| Признак равнобедренного треугольника: высота треугольника, совпадающая с медианой |
 Признак: Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным |
| Признак равнобедренного треугольника: высота т? |
