Каким свойством обладают точки биссектрисы угла
Мария Полютова · 20 февраля 2019
13,2 K
Имею естественно научное образование, в юношестве прикипел к литературе, сейчас…
Основные свойства бисскетрисы:
- Делит противовположные стороны на части, которые пропорциональные прилегающим сторонам
- Все биссектрисы пересекаются в точке внутри треугольника, и эта точка является центром окружности, вписанной в треугольник
- Точки биссектрисы равноудалены от точек ее угла
- Бисскетрисы внешнего и внутреннего уголов прямоугольника являются перпендикулярными
- Бисскетриса является и медианой и высотой только в правильном треугольнике
Биссектриса является медийной и высотой и в равнобедренном треугольнике
В определении биссектрисы треугольника лежит то, что этот отрезок пересечет противоположную сторону треугольника, но почему? Где доказательство? С мат. точ.зр.
Веб-дизайнер, участник промо-группы, музыкант, фотограф, видеомейкер, предприним…
Не понимаю о чем вы спрашиваете, но биссектриса — это прямая, делящая угол пополам, проведенная от вершины угла до её пересечения с противолежащей стороной. Тут главное что она делит угол, а не то что она прикасается к стороне
Прочитать ещё 1 ответ
Чему равно число Пи?
Никто не знает точно, чему равно пи. Если разделить длину окружности на ее диаметр, то результат всегда будет одинаковый, какую окружность ни возьми. Этот результат и обозначили греческой буквой пи. Буква понадобилась потому, что привычными цифрами это число точно записать невозможно. Но мы знаем, чему оно равно приблизительно.
Самое знаменитое приближение – 3,14. Чтобы запомнить больше цифр, можно выучить стишок:
Надо очень постараться
И запомнить всё как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть
Прочитать ещё 15 ответов
Биссектриса угла цэ и дэ параллелограмма abcd пересекаются в точке l лежащей на стороне ab докажите что l середина ab?
Нравится познавать и наслаждаться этим миром
CI — биссектриса угла BCD, DI — биссектриса угла ADC. Значит угол BCI равен углу DCI, а угол ADI равен углу CDI. Прямая CI пересекает параллельные прямые AB и CD, значит угол BIC равен углу DCI, откуда следует, что треугольник IBC равнобедренный, в котором сторона IB равна BC. Аналогично треугольник AID также равнобедренный, в котором стороны AI и AD равны. Противоположные стороны параллелограмма попарно равны, значит BC=AD, а BC=BI и AD=AI, значит и AI=IB, что и показывает, что точка I делит отрезок AB пополам.
Прочитать ещё 2 ответа
Возможен ли не прямоугольный треугольник, в котором сумма квадратов двух сторон равна квадрату третьей стороны?
Я согласен с ответом от Uwe Boll, но постараюсь ответить более детально.
Вообще, если вам даны один угол и длина двух сторон, или два угла и длина одной стороны, или все три стороны, то они определяют остальные три элемента. Однако если вам даны три угла, то они определяют длину сторон с точностью до фактора.
В вашем вопросе, даны длины всех трех сторон с точностью до фактора:
fA, fB, и fC=f sqrt(A^2+B^2). Мы хотим понять почему никакой «гибкости» в этом треугольнике нет.
Обозначим углы напротив каждой из сторон соотвенственно a, b, c .
Мы используем закон косинусов на плоскости:
Косинус угла напротив «длинной» стороны (мы подозреваем, гипотенузы) определен
cos(c) = (A^2 + B^2 — C^2) / (2AB)
(фактор f сокращается). (Заметим, что два других угла тоже определены без всякой гибкости, но нам они не интересны.) Дальже идет алгебра — мы знаем длину C(A,B) и подставляем в правую сторону:
(A^2 + B^2 — C^2) / (2AB) = (A^2 + B^2 — sqrt(A^2+B^2)^2) / (2AB) = (A^2 + B^2 — (A^2+B^2)) / (2AB) = 0.
То есть косинус угла c = ноль. Значит это должен быть прямой угол.
Однако закон косинусов так не работает, если ваш треугольник не на плоскости, а, например, на сфере.
Прочитать ещё 2 ответа
2 июня 2018
Сегодня будет очень лёгкий урок. Мы рассмотрим всего один объект — биссектрису угла — и докажем важнейшее её свойство, которое очень пригодится нам в будущем.
Только не надо расслабляться: иногда ученики, желающие получить высокий балл на том же ОГЭ или ЕГЭ, на первом занятии даже не могут точно сформулировать определение биссектрисы.
И вместо того, чтобы заниматься действительно интересными задачами, мы тратим время на такие простые вещи. Поэтому читайте, смотрите — и берите на вооружение.:)
Для начала немного странный вопрос: что такое угол? Правильно: угол — это просто два луча, выходящих из одной точки. Например:
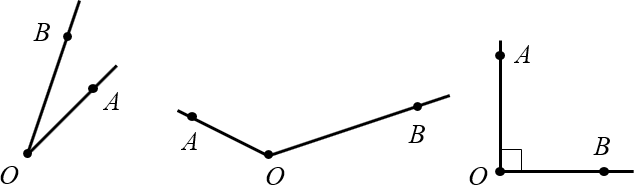Примеры углов: острый, тупой и прямой
Как видно из картинки, углы могут быть острыми, тупыми, прямыми — это сейчас неважно. Часто для удобства на каждом луче отмечают дополнительную точку и говорят, мол, перед нами угол $AOB$ (записывается как $angle AOB$).
Капитан очевидность как бы намекает, что помимо лучей $OA$ и $OB$ из точки $O$ всегда можно провести ещё кучу лучей. Но среди них будет один особенный — его-то и называют биссектрисой.
Определение. Биссектриса угла — это луч, который выходит из вершины этого угла и делит угол пополам.
Для приведённых выше углов биссектрисы будут выглядеть так:
Примеры биссектрис для острого, тупого и прямого угла
Поскольку на реальных чертежах далеко не всегда очевидно, что некий луч (в нашем случае это луч $OM$) разбивает исходный угол на два равных, в геометрии принято помечать равные углы одинаковым количеством дуг (у нас на чертеже это 1 дуга для острого угла, две — для тупого, три — для прямого).
Хорошо, с определением разобрались. Теперь нужно понять, какие свойства есть у биссектрисы.
Основное свойство биссектрисы угла
На самом деле у биссектрисы куча свойств. И мы обязательно рассмотрим их в следующем уроке. Но есть одна фишка, которую нужно понять прямо сейчас:
Теорема. Биссектриса угла — это геометрическое место точек, равноудалённых от сторон данного угла.
В переводе с математического на русский это означает сразу два факта:
- Всякая точка, лежащая на биссектрисе некого угла, находится на одинаковом расстоянии от сторон этого угла.
- И наоборот: если точка лежит на одинаковом расстоянии от сторон данного угла, то она гарантированно лежит на биссектрисе этого угла.
Прежде чем доказывать эти утверждения, давайте уточним один момент: а что, собственно, называется расстоянием от точки до стороны угла? Здесь нам поможет старое-доброе определение расстояния от точки до прямой:
Определение. Расстояние от точки до прямой — это длина перпендикуляра, проведённого из данной точки к этой прямой.
Например, рассмотрим прямую $l$ и точку $A$, не лежащую на этой прямой. Проведём перпендикуляр $AH$, где $Hin l$. Тогда длина этого перпендикуляра и будет расстоянием от точки $A$ до прямой $l$.
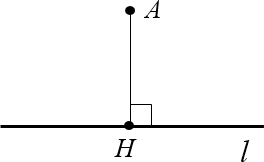Графическое представление расстояния от точки до прямой
Поскольку угол — это просто два луча, а каждый луч — это кусок прямой, легко определить расстояние от точки до сторон угла. Это просто два перпендикуляра:
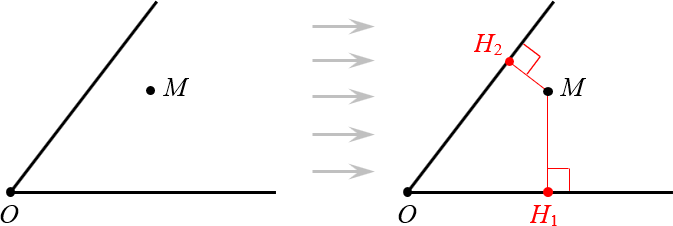Определяем расстояние от точки до сторон угла
Вот и всё! Теперь мы знаем, что такое расстояние и что такое биссектриса. Поэтому можно доказывать основное свойство.
Как и обещал, разобьём доказательство на две части:
1. Расстояния от точки на биссектрисе до сторон угла одинаковы
Рассмотрим произвольный угол с вершиной $O$ и биссектрисой $OM$:
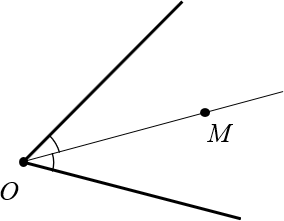
Докажем, что эта самая точка $M$ находится на одинаковом расстоянии от сторон угла.
Доказательство. Проведём из точки $M$ перпендикуляры к сторонам угла. Назовём их $M{{H}_{1}}$ и $M{{H}_{2}}$:
Провели перпендикуляры к сторонам угла
Получили два прямоугольных треугольника: $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$. У них общая гипотенуза $OM$ и равные углы:
- $angle MO{{H}_{1}}=angle MO{{H}_{2}}$ по условию (поскольку $OM$ — биссектриса);
- $angle M{{H}_{1}}O=angle M{{H}_{2}}O=90{}^circ $ по построению;
- $angle OM{{H}_{1}}=angle OM{{H}_{2}}=90{}^circ -angle MO{{H}_{1}}$, поскольку сумма острых углов прямоугольного треугольника всегда равна 90 градусов.
Следовательно, треугольники равны по стороне и двум прилежащим углам (см. признаки равенства треугольников). Поэтому, в частности, $M{{H}_{2}}=M{{H}_{1}}$, т.е. расстояния от точки $O$ до сторон угла действительно равны. Что и требовалось доказать.:)
2. Если расстояния равны, то точка лежит на биссектрисе
Теперь обратная ситуация. Пусть дан угол $O$ и точка $M$, равноудалённая от сторон этого угла:
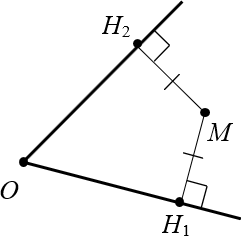
Докажем, что луч $OM$ — биссектриса, т.е. $angle MO{{H}_{1}}=angle MO{{H}_{2}}$.
Доказательство. Для начала проведём этот самый луч $OM$, иначе доказывать будет нечего:
Провели луч $OM$ внутри угла
Снова получили два прямоугольных треугольника: $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$. Очевидно, что они равны, поскольку:
- Гипотенуза $OM$ — общая;
- Катеты $M{{H}_{1}}=M{{H}_{2}}$ по условию (ведь точка $M$ равноудалена от сторон угла);
- Оставшиеся катеты тоже равны, т.к. по теореме Пифагора $OH_{1}^{2}=OH_{2}^{2}=O{{M}^{2}}-MH_{1}^{2}$.
Следовательно, треугольники $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$ по трём сторонам. В частности, равны их углы: $angle MO{{H}_{1}}=angle MO{{H}_{2}}$. А это как раз и означает, что $OM$ — биссектриса.
В заключение доказательства отметим красными дугами образовавшиеся равные углы:
Биссектриса разбила угол $angle {{H}_{1}}O{{H}_{2}}$ на два равных
Как видите, ничего сложного. Мы доказали, что биссектриса угла — это геометрическое место точек, равноудалённых до сторон этого угла.:)
Теперь, когда мы более-менее определились с терминологией, пора переходить на новый уровень. В следующем уроке мы разберём более сложные свойства биссектрисы и научимся применять их для решения настоящих задач.
Смотрите также:
- Высота в треугольнике
- Основное свойство биссектрисы угла в треугольнике и его применение для решения задач
- Тест к уроку «Площади многоугольников на координатной сетке» (легкий)
- Правила вычисления производных
- Сводный тест по задачам B15 (2 вариант)
- Симметрия корней и оптимизация ответов в тригонометрии
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Биссектриса треугольника и ее свойства
СОДЕРЖАНИЕ СТАТЬИ
Знаешь ли ты, что такое середина отрезка? Конечно же знаешь. А центр круга? Тоже.
А что такое середина угла?
Ты можешь сказать, что такого не бывает. Но почему же, отрезок можно разделить пополам, а угол нельзя? Вполне можно – только не точкой, а…. линией.
Помнишь шутку: биссектриса это крыса, которая бегает по углам и делит угол пополам.
Так вот, настоящее определение биссектрисы очень похоже на эту шутку:
 | Биссектриса – это линия, делящая угол пополам. |
Биссектриса треугольника — это отрезок биссектрисы угла треугольника, соединяющий вершину этого угла с точкой на противолежащей стороне.
Когда-то древние астрономы и математики открыли очень много интересных свойств биссектрисы. Эти знания сильно упростили жизнь людей.
Стало легче строить, считать расстояния, даже корректировать стрельбу из пушек… Нам же знание этих свойств поможет решить некоторые задания ОГЭ и ЕГЭ!
Первое знание, которое поможет в этом — это…
Биссектриса равнобедренного треугольника
 | Биссектриса равнобедренного треугольника, проведенная к основанию, является и медианой, и высотой. |
Кстати, а помнишь ли ты все эти термины? Помнишь чем они отличаются друг от друга? Нет? Не страшно. Сейчас разберемся.
Итак,
- Основание равнобедренного треугольника – это та сторона, которая не равна никакой другой. Посмотри на рисунок, как ты думаешь, какая это сторона? Правильно — это сторона .
- Медиана – это линия, проведенная из вершины треугольника и делящая противоположную сторону (это снова ) пополам. Заметь, мы не говорим: «Медиана равнобедренного треугольника». А знаешь почему? Потому что медиана, проведенная из вершины треугольника, делит противоположную сторону пополам в ЛЮБОМ треугольнике.
- Высота – это линия, проведенная из вершины и перпендикулярная основанию. Ты заметил? Мы опять говорим о любом треугольнике, а не только о равнобедренном. Высота в ЛЮБОМ треугольнике всегда перпендикулярна основанию.
Итак, разобрались? Ну почти.
Чтобы еще лучше понять и навсегда запомнить что такое биссектриса, медиана и высота, их нужно сравнить друг с другом и понять в чем они похожи и чем они отличаются друг от друга.
При этом, чтобы лучше запомнить, лучше описать все «человеческим языком».
Потом ты легко будешь оперировать языком математики, но сначала ты этот язык не понимаешь и тебе нужно осмыслить все на своем языке.
Итак, в чем они похожи?
Биссектриса, медиана и высота – все они «выходят» из вершины треугольника и упираются в противоположную сторону и «что-то делают» либо с углом из которого выходят, либо с противоположной стороной.
По-моему просто, нет? А чем они отличаются?
Чем отличаются друг от друга биссектриса, медиана и высота?
- Биссектриса делит угол, из которого выходит, пополам.
- Медиана делит противоположную сторону пополам.
- Высота всегда перпендикулярна противоположной стороне.
Теперь все. Понять – легко. А раз понял, можешь запомнить.
Теперь следующий вопрос.
Почему же в случае с равнобедренным треугольником биссектриса оказывается одновременно и медианой и высотой?
Можно просто посмотреть на рисунок и убедиться, что медиана разбивает на два абсолютно равных треугольника.
Вот и все! Но математики не любят верить своим глазам. Им нужно все доказывать.
Страшное слово?
Ничего подобного — все просто! Смотри: у и равны стороны и , сторона у них вообще общая и . ( – биссектриса!) И вот, получилось, что два треугольника имеют по две равные стороны и угол между ними.
Вспоминаем первый признак равенства треугольников (не помнишь, загляни в тему «Треугольник») и заключаем, что , а значит = и .
= – это уже хорошо – значит, оказалась медианой.
А вот что такое ?
Посмотрим на картинку — . А у нас получилось, что . Значит, и тоже! Наконец, ура! и .
Показалось ли тебе это доказательство тяжеловатым? Посмотри на картинку – два одинаковых треугольника говорят сами за себя.
В любом случае твердо запомни:
Биссектриса, проведенная к основанию равнобедренного треугольника, делит это основание пополам и перпендикулярна ему.
Готов дальше?
Теперь сложнее…
Посчитаем угол между биссектрисами в любом треугольнике!
Не бойся, все не так уж хитро. Смотри на рисунок:
 | B проведем две биссектрисы и . Они пересеклись – а куда деваться-то? Какой же угол получился у точки ? |
Давай его посчитаем. Ты помнишь, что сумма углов треугольника равна ?
Применим этот потрясающий факт.
С одной стороны, из :
, то есть .
Теперь посмотрим на :
Но биссектрисы, биссектрисы же!
Значит
, то есть
Вспомним про :
Значит,
Теперь через буквы
Не удивительно ли?
Получилось, что угол между биссектрисами двух углов зависит только от третьего угла!
Ну вот, две биссектрисы мы посмотрели. А что, если их три??!! Пересекутся ли они все в одной точке?
Или будет так?
Как ты думаешь? Вот математики думали-думали и доказали:
Три биссектрисы треугольника (любого!) пересекаются в одной точке – и эта точка – центр вписанной окружности.
Правда, здорово?
Хочешь знать, почему же так получается?
Переходи на следующий уровень – ты готов к покорению новых вершин знаний о биссектрисе!
БИССЕКТРИСА. СРЕДНИЙ УРОВЕНЬ
Биссектриса – это линия, которая делит угол пополам.
Тебе встретилась в задаче биссектриса? Постарайся применить одно (а иногда можешь и несколько) из следующих потрясающих свойств.
1. Биссектриса в равнобедренном треугольнике.
Не боишься слова «теорема»? Если боишься, то – зря. Теоремой математики привыкли называть всякое утверждение, которое можно как-то вывести из других, более простых утверждений.
Так вот, внимание, теорема!
Теорема. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.
Докажем эту теорему, то есть поймём, почему же так получается? Посмотри на равнобедренный .
 | В нём и проведена биссектриса . Видишь: получилось два треугольника . и . |
Давай посмотрим на них внимательно. И тогда увидим, что
- — общая.
А это значит (скорее вспоминай первый признак равенства треугольников!), что .
Ну и что? Хочется тебе так сказать? А то, что мы ещё не смотрели на третьи стороны и оставшиеся углы этих треугольников.
А вот теперь посмотрим. Раз , то совершенно точно и даже вдобавок, .
Вот и получилось, что
- разделила сторону пополам, то есть оказалась медианой
- , а значит, они оба по , так как (глянь ещё раз на рисунок).
Вот и оказалась биссектриса и высотой тоже!
Ура! Доказали теорему. Но представляешь, это ещё не всё. Верна ещё и обратная теорема:
Теорема. Если в треугольнике биссектриса, проведённая из какого-то угла, совпадает с медианой или с высотой, то этот треугольник равнобедренный.
Доказательство? Неужели тебе интересно? Читай следующий уровень теории!
А если неинтересно, то твердо запомни:
Биссектриса совпадает с высотой и медианой только в равнобедренном треугольнике!
Зачем же это твердо запоминать? Как это может помочь? А вот представь, что у тебя задача:
Дано: .
Найти: .
Ты тут же соображаешь, биссектриса и, о чудо, она разделила сторону пополам! (по условию…). Если ты твердо помнишь, что так бывает только в равнобедренном треугольнике, то делаешь вывод, что и значит, пишешь ответ: . Здорово, правда? Конечно, не во всех задачах будет так легко, но знание обязательно поможет!
А теперь следующее свойство. Готов?
2. Биссектриса угла – геометрическое место точек, равноудалённых от сторон угла.
Испугался? На самом деле ничего страшного. Ленивые математики в двух строчках спрятали четыре. Итак, что же значит, «Биссектриса – геометрическое место точек»? А это значит, что выполняются сразу дваутверждения:
- Если точка лежит на биссектрисе, то расстояния от неё до сторон угла равны.
- Если у какой-нибудь точки расстояния до сторон угла равны, то эта точка обязательно лежит на биссектрисе.
Видишь разницу между утверждениями 1 и 2? Если не очень, то вспомни Шляпника из «Алисы в стране чудес»: «Так ты еще чего доброго скажешь, будто «Я вижу то, что ем» и «Я ем то, что вижу», — одно и то же!»
Итак, нам нужно доказать утверждения 1 и 2, и тогда утверждение: «биссектриса – это геометрическое место точек, равноудаленных от сторон угла» будет доказано!
Почему же верно 1?
Возьмём любую точку на биссектрисе и назовём её .
Опустим из этой точки перпендикуляры и на стороны угла.
А теперь …приготовились вспоминать признаки равенства прямоугольных треугольников! Если ты их подзабыл, то загляни в раздел «Прямоугольный треугольник».
Итак…два прямоугольных треугольника: и . У них:
- Общая гипотенуза .
- (потому что – биссектриса!)
Значит, — по углу и гипотенузе. Поэтому и соответствующие катеты у этих треугольников – равны! То есть .
Доказали, что точка одинаково (или равно) удалена от сторон угла. С пунктом 1 разобрались. Теперь перейдём к пункту 2.
Почему же верно 2?
 | Возьмем какую-то точку внутри угла, для которой расстояние до сторон угла равны. |
И соединим точки и .
| Теперь как прямоугольные по катету и гипотенузе. |
Значит, , то есть лежит на биссектрисе!
Вот и всё!
Как же все это применить при решении задач? Вот например, в задачах часто бывает такая фраза: «Окружность касается сторон угла….». Ну, и найти нужно что-то.
То быстро соображаешь, что
 |
|
И можно пользоваться равенством .
3. Три биссектрисы в треугольнике пересекаются в одной точке
Из свойства биссектрисы быть геометрическим местом точек, равноудаленных от сторон угла, вытекает следующее утверждение:
Три биссектрисы в треугольнике пересекаются в одной точке, и эта точка – центр вписанной в треугольник окружности.
Как именно вытекает? А вот смотри: две-то биссектрисы точно пересекутся, правда?
А третья биссектриса могла бы пройти так:
Но на самом деле-то всё гораздо лучше!
Давай рассмотрим точку пересечения двух биссектрис. Назовём её .
 | Эта точка лежит на биссектрисе . Что из этого следует? Правильно! ! Точка лежит ещё и на биссектрисе , поэтому . |
Что мы тут оба раза применяли? Да пункт 1, конечно же! Если точка лежит на биссектрисе, то она одинаково удалена от сторон угла.
Вот и получилось и .
Но посмотри внимательно на эти два равенства! Ведь из них следует, что и, значит, .
А вот теперь в дело пойдёт пункт 2: если расстояния до сторон угла равны, то точка лежит на биссектрисе…какого же угла? Ещё раз смотри на картинку:
и – расстояния до сторон угла , и они равны, значит, точка лежит на биссектрисе угла . Третья биссектриса прошла через ту же точку! Все три биссектрисы пересеклись в одной точке! И, как дополнительный подарок —
— радиусы вписанной окружности.
(Для верности посмотри ещё тему «Вписанная окружность»).
Ну вот, теперь ты никогда не забудешь:
Точка пересечения биссектрис треугольника – центр вписанной в неё окружности.
Переходим к следующему свойству… Ух и много же свойств у биссектрисы, правда? И это здорово, потому что, чем больше свойств, тем больше инструментов для решения задач про биссектрису.
4. Биссектриса и параллельность, биссектрисы смежных углов
Тот факт, что биссектриса делит угол пополам, в каких-то случаях приводит к совершенно неожиданным результатам. Вот, например,
Случай 1
Биссектриса угла параллелограмма отсекает равнобедренный треугольник.
Здорово, правда? Давай поймём, почему так.
С одной стороны, — мы же проводим биссектрису!
Но, с другой стороны, — как накрест лежащие углы (вспоминаем тему «Параллельные прямые»).
И теперь выходит, что ; выкидываем середину: ! – равнобедренный!
Случай 2
Биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.
Представь треугольник (или посмотри на картинку)
Давай продолжим сторону за точку . Теперь получилось два угла :
- – внутренний угол
- – внешний угол – он же снаружи, верно?
Так вот, а теперь кому-то захотелось провести не одну, а сразу две биссектрисы: и для , и для . Что же получится?
А получится прямоугольный !
Удивительно, но это именно так.
Разбираемся.
Как ты думаешь, чему равна сумма ?
Конечно же, — ведь они все вместе составляют такой угол, что получается прямая .
А теперь вспомним, что и –биссектрисы и увидим, что внутри угла находится ровно половина от суммы всех четырех углов: и — – то есть ровно . Можно написать и уравнением:
Итак, невероятно, но факт:
Угол между биссектрисами внутреннего и внешнего угла треугольника равен .
Случай 3
Биссектрисы односторонних углов параллелограмма и трапеции пересекаются под прямым углом.
Видишь, что здесь все так же, как и для внутреннего и внешнего углов?
Или ещё раз подумаем, почему так получается?
Снова, как и для смежных углов,
(как соответственные при параллельных основаниях).
И опять, составляют ровно половину от суммы
Значит, .
Вывод: Если в задаче встретились биссектрисы смежных углов или биссектрисы соответственных углов параллелограмма или трапеции, то в этой задаче непременно участвует прямоугольный треугольник, а может даже и целый прямоугольник.
5. Биссектриса и противоположная сторона
Оказывается, биссектриса угла треугольника делит противоположную сторону не как-нибудь, а специальным и очень интересным образом:
 |
То есть:
Удивительный факт, не правда ли?
Сейчас мы этот факт докажем, но приготовься: будет немного сложнее, чем раньше.
Снова – выход в «космос» — дополнительное построение!
Проведём прямую .
Зачем? Сейчас увидим.
Продолжим биссектрису до пересечения с прямой .
Знакомая картинка? Да-да-да, точно так же, как в пункте 4, случай 1 – получается, что ( – биссектриса)
— как накрест лежащие
и
Значит, – это тоже .
А теперь посмотрим на треугольники и .
Что про них можно сказать?
Они…подобны. Ну да, у них и углы равны как вертикальные. Значит, по двум углам.
Теперь имеем право писать отношения соответствующих сторон.
А теперь в коротких обозначениях:
Ой! Что-то напоминает, верно? Не это ли самое мы хотели доказать? Да-да, именно это!
Видишь, как здорово проявил себя «выход в космос» — построение дополнительной прямой – без неё ничего бы не вышло! А так, мы доказали, что
|
Теперь можешь смело использовать! Разберём ещё одно свойство биссектрис углов треугольника – не пугайся, теперь самое сложное кончилось – будет проще.
6. Угол между биссектрисами треугольника
 | Пусть и – биссектрисы. Найдём (помним, что сумма углов треугольника равна ). |
Получаем, что
Это знание можно применить в тех задачах, где участвуют две биссектрисы и дан лишь угол , а искомые величины выдерживаются через или, наоборот, дан, а нужно найти что-то с участием угла .
Основные знания о биссектрисе закончились. Комбинируя эти факты, ты найдёшь ключ к любой задаче о биссектрисе!
БИССЕКТРИСА. КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ
|
|
| Биссектриса треугольника — это отрезок биссектрисы угла треугольника, соединяющий вершину этого угла с точкой на противолежащей стороне. |
Теорема 1:
| Три биссектрисы в треугольнике пересекаются в одной точке, и эта точка – центр вписанной в треугольник окружности. |
Теорема 2:
 | В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой. |
Теорема 3:
| Биссектриса угла параллелограмма отсекает равнобедренный треугольник. |
Теорема 4:
| Биссектрисы внутреннего и внешнего углов треугольника перпендикулярны. |
Теорема 5:
| Биссектрисы односторонних углов параллелограмма и трапеции пересекаются под прямым углом. |
Теорема 6:
| Отношение отрезков, на которые биссектриса делит противоположную сторону, такое же, как и отношение двух сторон, между которыми эта биссектриса прошла. |
ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!
Стать учеником YouClever,
Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц»,
А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.