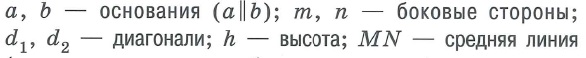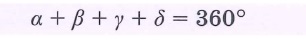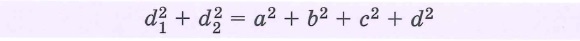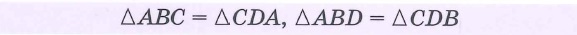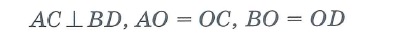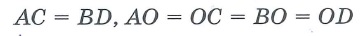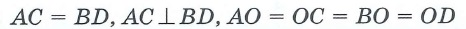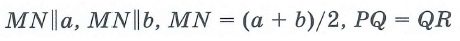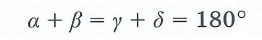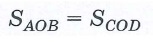Каким свойством обладают стороны четырехугольника

Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. Свойства параллелограмма. Свойства ромба. Свойства прямоугольника. Свойства квадрата. Свойства трапеции. Примерно 7-9 класс (13-15 лет)
Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Виды четырехугольников: | |||
|  | ||
|  | ||
|  | ||
|  | ||
|  | ||
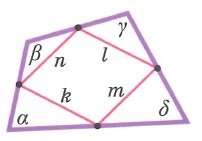
Свойства произвольных четырехугольников: | |||
|  | ||
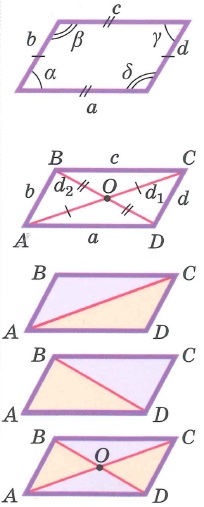
Свойства параллелограмма: | |||
|  | ||
Свойства ромба: | |||
| 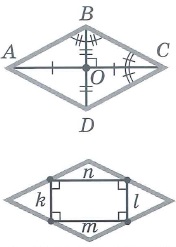 | ||
Свойства прямоугольника: | |||
| 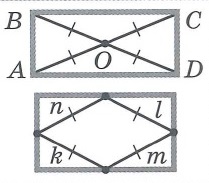 | ||
Свойства квадрата: | |||
|  | ||
Свойства трапеции: | |||
| 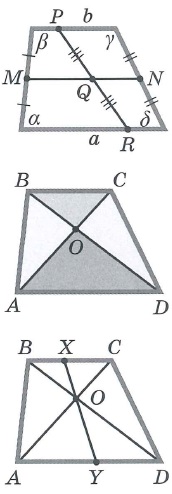 | ||
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers
Консультации и техническая
поддержка сайта: Zavarka Team
Free xml sitemap generator
Четырехугольником ABCD называется фигура, которая состоит из четырех точек А, В, С, D по три, не лежащих на одной прямой, и четырех отрезков AB, BC, CD и AD, соединяющих эти точки.
На рисунках изображены четырехугольники.
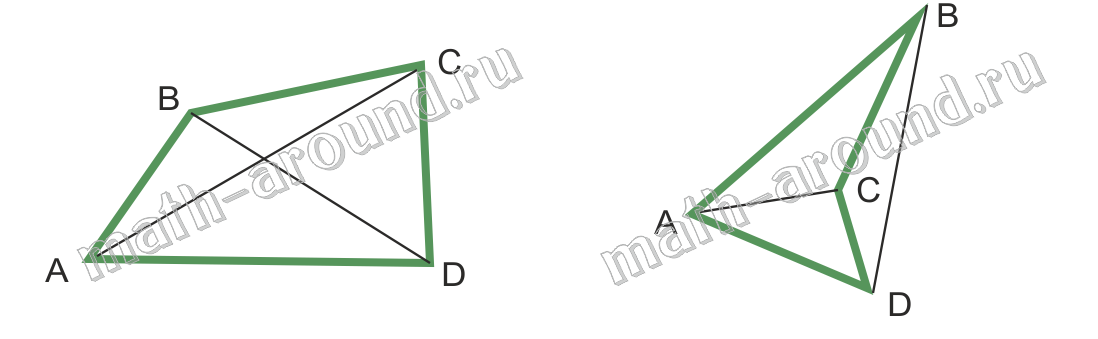
Точки А, В, С и D называются вершинами четырехугольника, а отрезки AB, BC, CD и AD — сторонами. Вершины А и С, В и D называются противолежащими вершинами. Стороны AB и CD, BC и AD называются противолежащими сторонами.
Четырехугольники бывают выпуклые (на рисунке — левый) и невыпуклые (на рисунке — правый).
Каждая диагональ выпуклого четырехугольника разделяет его на два треугольника (диагональ АС разделяет ABCD на два треугольника ABC и ACD; диагональ BD — на BCD и BAD). У невыпуклого четырехугольника только одна из диагоналей разделяет его на два треугольника (диагональ AC разделяет ABCD на два треугольника ABC и ACD; диагональ BD — не разделяет).
Рассмотрим основные виды четырехугольников, их свойства, формулы площади:
Параллелограмм
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
 | ABCD-параллелограмм: AB||DC, AD||BC |
Свойства:
|  |
| 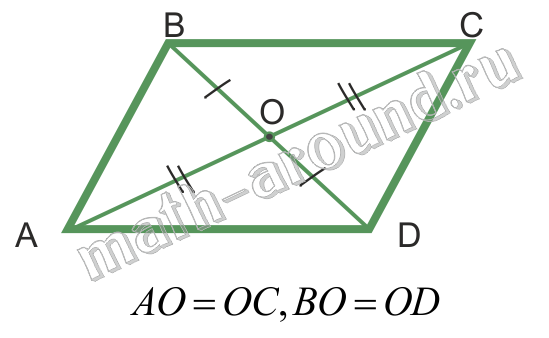 |
Признаки параллелограмма:
1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.
2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Площадь параллелограмма:
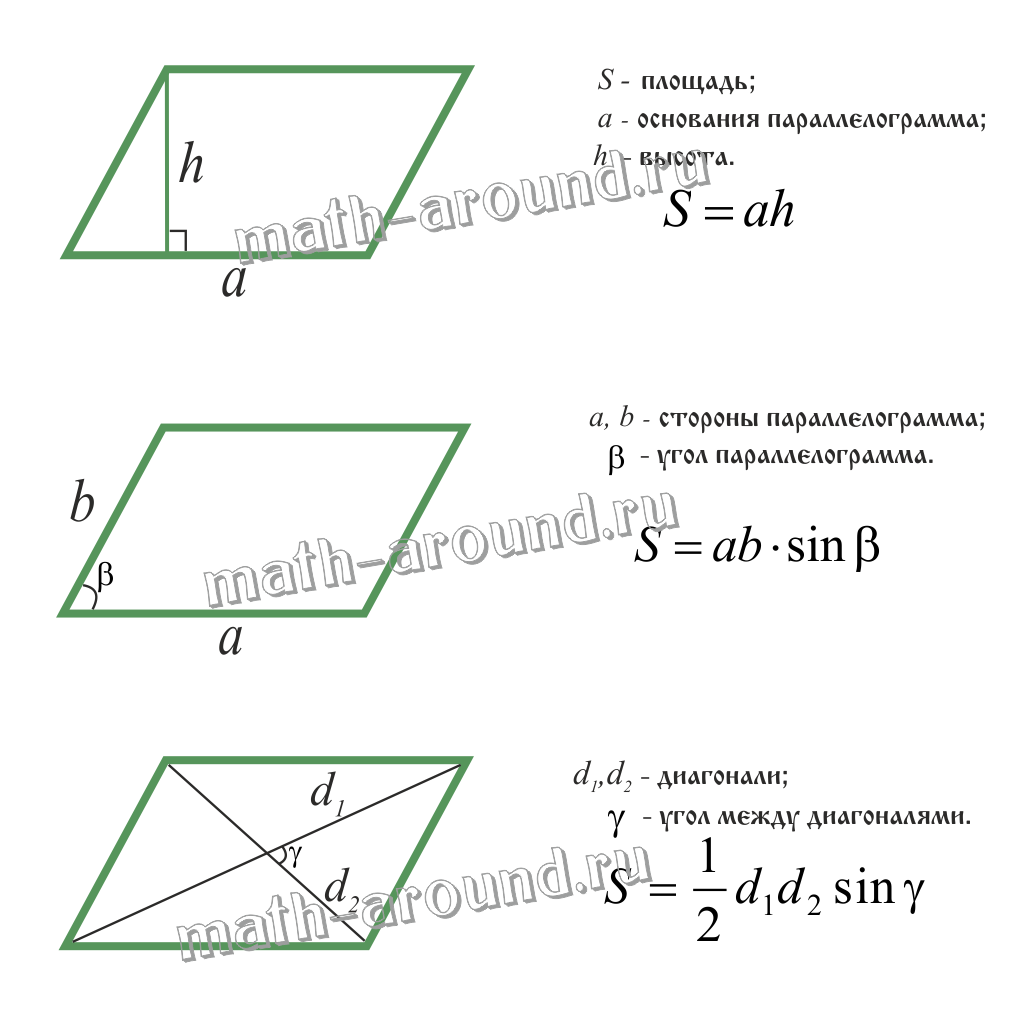
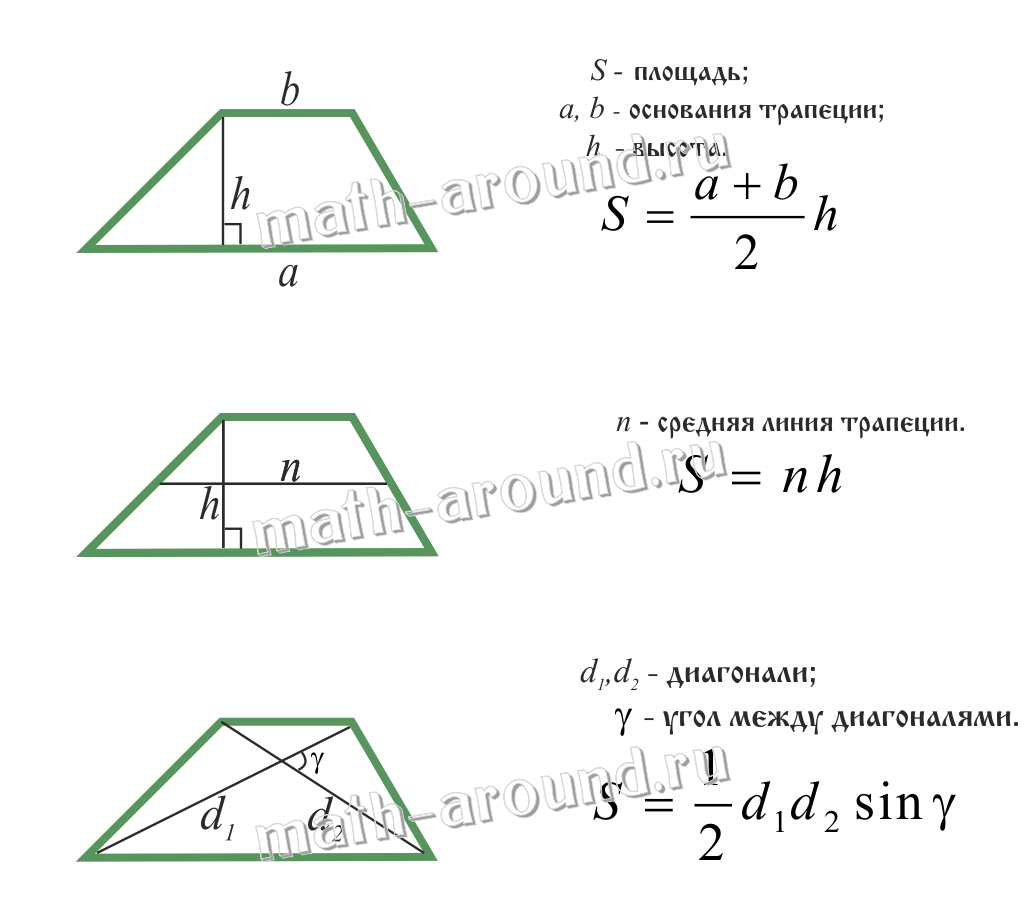
Трапеция
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Основаниями называются параллельные стороны, а две другие стороны — боковыми сторонами.
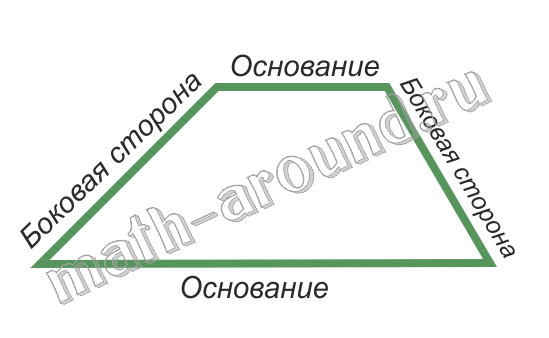
Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.
ТЕОРЕМА.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
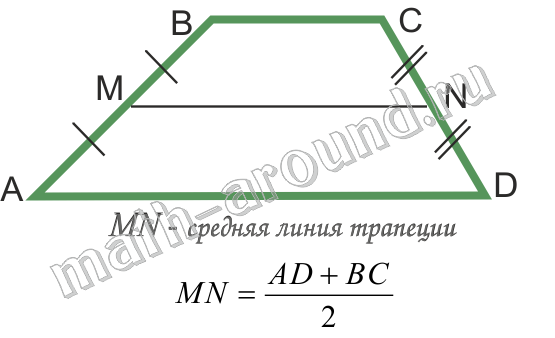
Площадь трапеции:
Ромб
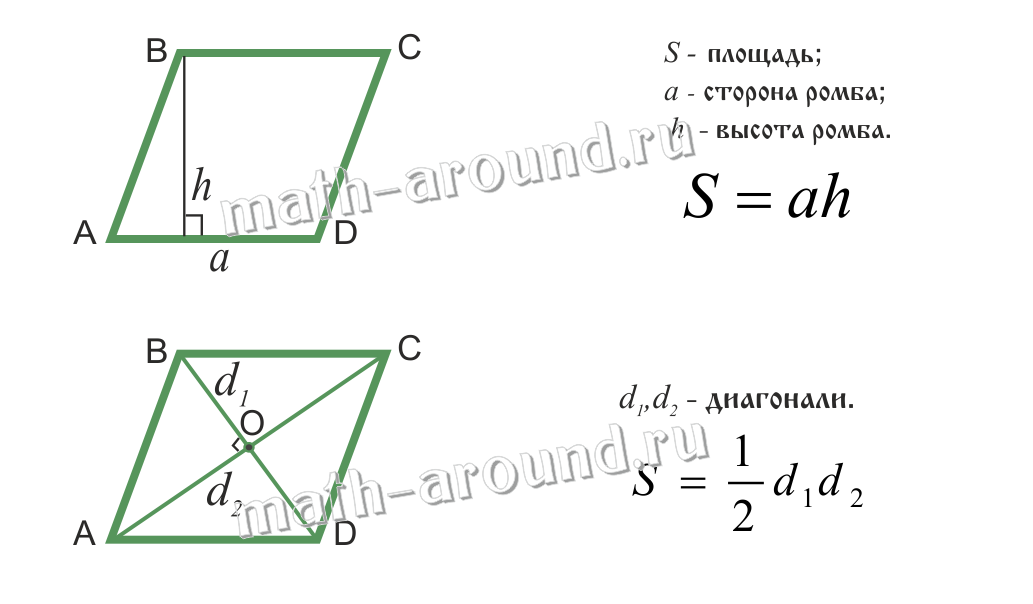
Ромбом называется параллелограмм, у которого все стороны равны.
Свойства:
|  |
|  |
Площадь ромба:
Прямоугольник
Прямоугольником называется параллелограмм, у которого все углы равны.
Свойства:
|  |
|  |
Признак прямоугольника:
Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
Площадь прямоугольника:

Квадрат
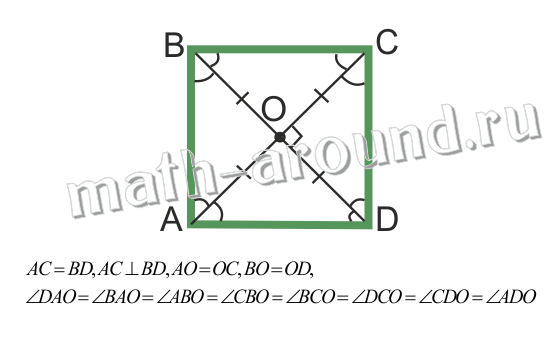
Квадратом называется прямоугольник, у которого все стороны равны.
Свойства:
Квадрат обладает всеми свойствами прямоугольника и ромба (прямоугольник является параллелограммом, поэтому и квадрат является параллелограммом, у которого все стороны равны, т.е. ромбом).
|  |
|  |
Площадь квадрата: