Каким свойством обладают противолежащие углы параллелограмма

Ñâîéñòâà ñòîðîí è óãëîâ ïàðàëëåëîãðàììà.
Ó ïàðàëëåëîãðàììà ïðîòèâîïîëîæíûå ñòîðîíû èìåþò îäèíàêîâóþ äëèíó, à ïðîòèâîïîëîæíûå óãëû ðàâíóþ âåëè÷èíó.

Äàíî:
ABCD — ïàðàëëåëîãðàìì.
Äîêàçàòü:
AB=CD, AD=BC,
∠A=∠C, ∠B=∠D.
Äîêàçàòåëüñòâî:
Ïðîâîäèì â ïàðàëëåëîãðàììå ABCD äèàãîíàëü BD.

Ðàññìàòðèâàåì òðåóãîëüíèêè ABD è CDB. Çäåñü âàæíî ïðàâèëüíî óêàçàòü òðåóãîëüíèêè.
1) Ñòîðîíà BD ÿâëÿåòñÿ îáùåé.
2) ∠ABD=∠CDB (êàê âíóòðåííèå íàêðåñò ëåæàùèå ïðè AB∥CD è ñåêóùåé BD)
3) ∠ADB=∠CBD (êàê âíóòðåííèå íàêðåñò ëåæàùèå ïðè AD∥BC è ñåêóùåé BD)
Òî åñòü, ∆ABD= ∆CDB (ïî ñòîðîíå è 2-ì ïðèëåæàùèì ê íåé óãëàì).
Èç ðàâåíñòâà òðåóãîëüíèêîâ ñëåäóåò ðàâåíñòâî ñîîòâåòñòâóþùèõ ñòîðîí:
AB=CD, AD=BC
è ðàâåíñòâî ñîîòâåòñòâóþùèõ óãëîâ:
∠A=∠C.
 ïóíêòàõ 2) è 3) îáúÿñíåíî, ÷òî ∠ABD=∠CDB è ∠ADB=∠CB.
Çíà÷èò,
∠ABC=∠ABD+∠CBD=∠CDB+∠ADB=∠ADC,
Ò.å., ∠B=∠D. ×òî è òðåáîâàëîñü äîêàçàòü.
Ñâîéñòâî óãëîâ ïàðàëëåëîãðàììà, ïðèëåæàùèõ ê îäíîé ñòîðîíå.
Ñóììà óãëîâ ïàðàëëåëîãðàììà, êîòîðûå ïðèëåæàò ê îäíîé ñòîðîíå ñîîòâåòñòâóåò 180 ãðàäóñàì.
Ýòî ñâîéñòâî âûõîäèò èç òîãî, ÷òî óãëû, êîòîðûå ïðèëåæàò ê 1-îé ñòîðîíå ïàðàëëåëîãðàììà îêàçûâàþòñÿ âíóòðåííèìè îäíîñòîðîííèìè óãëàìè ïðè ïàðàëëåëüíûõ ïðÿìûõ.
Äëÿ ïàðàëëåëîãðàììà ABCD:
∠A+∠B=180º (êàê âíóòðåííèå îäíîñòîðîííèå ïðè AD∥BC è ñåêóùåé AB;
∠C+∠D=180º (êàê âíóòðåííèå îäíîñòîðîííèå ïðè AD∥BC è ñåêóùåé CD;
∠A+∠D=180º (êàê âíóòðåííèå îäíîñòîðîííèå ïðè AB∥CD è ñåêóùåé AD;
∠B+∠C=180º (êàê âíóòðåííèå îäíîñòîðîííèå ïðè AB∥CD è ñåêóùåé BC.
Åùå íåêîòîðûå ñâîéñòâà óãëîâ ïàðàëëåëîãðàììà:
Áèññåêòðèñû óãëîâ ïàðàëëåëîãðàììà, êîòîðûå ïðèëåæàò ê îäíîé ñòîðîíå, — ïåðïåíäèêóëÿðíû.
Áèññåêòðèñû ïðîòèâîëåæàùèõ óãëîâ ïàðàëëåëîãðàììà — ïàðàëëåëüíû.
Áèññåêòðèñà óãëà ïàðàëëåëîãðàììà îòñåêàåò îò íåãî ðàâíîáåäðåííûé òðåóãîëüíèê.
Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
| Ïîìîùü â ðåøåíèè çàäà÷ ïî ãåîìåòðèè, ó÷åáíèê îíëàéí (âñå êàëüêóëÿòîðû ïî ãåîìåòðèè). | |
| Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
Ãåîìåòðè÷åñêèå ôèãóðû. | |
| Ãåîìåòðè÷åñêèå ôèãóðû — ïèðàìèäà, ïðÿìîóãîëüíèê, ðîìá, óãëû, øàð, ïàðàëëåëîãðàìì, ïàðàëëåëåïèïåä, ïðèçìà, ñâîéñòâà, ôîðìóëû ãåîìåòðè÷åñêèõ ôèãóð | |
| Ãåîìåòðè÷åñêèå ôèãóðû. | |
Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ãåîìåòðèè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
Ãåîìåòðè÷åñêèå ôèãóðû. Ïðàâèëüíàÿ ïèðàìèäà. | |
| Ïðàâèëüíàÿ ïèðàìèäà — êîãäà îñíîâàíèåì ïèðàìèäû ÿâëÿåòñÿ ïðàâèëüíûé ìíîãîóãîëüíèê, à âûñîòà ïðîåöèðóåòñÿ â öåíòð îñíîâàíèÿ (èëè ïðîõîäèò ÷åðåç íåãî). | |
| Ãåîìåòðè÷åñêèå ôèãóðû. Ïðàâèëüíàÿ ïèðàìèäà. | |
Ãåîìåòðè÷åñêèå ôèãóðû. Ïðèçìà. Îáúåì ïðèçìû. | |
| Ïðèçìà ìíîãîãðàííèê, 2 ãðàíè ýòî êîíãðóýíòíûå (ðàâíûå) ìíîãîóãîëüíèêè, êîòîðûå ëåæàò â ïàðàëëåëüíûõ ïëîñêîñòÿõ, à îñòàâøèåñÿ ãðàíè ïàðàëëåëîãðàììû, èìåþùèå îáùèå ñòîðîíû ñ ýòèìè ìíîãîóãîëüíèêàìè. | |
| Ãåîìåòðè÷åñêèå ôèãóðû. Ïðèçìà. Îáúåì ïðèçìû. | |
БИЛЕТ№4.
ПОВОРОТ.
ПРИЗНАК ПРОТИВОЛЕЖАЩИХ СТОРОН ПАРАЛЛЕЛОГРАММА.
БИЛЕТ№5.
СИММЕТРИЯ ОТНОСИТЕЛЬНО ПРЯМОЙ.
Пусть g — фиксированная прямая (рис. 191). Возьмем произвольную точку X и опустим перпендикуляр АХ на прямую g. На продолжении перпендикуляра за точку А отложим отрезок АХ’, равный отрезку АХ. Точка X’ называется симметричной точке X относительно прямой g. Если точка X лежит на прямой g, то симметричная ей точка есть сама точка X. Очевидно, что точка, симметричная точке Х’ есть точка X.
Преобразование фигуры F в фигуру F’, при котором каждая ее точка X переходит в точку X’, симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g. При этом фигуры F и F’ называются симметричными относительно прямой g (рис. 192).
Если преобразование симметрии относительно прямой g переводит фигуру F в себя, то эта фигура называется симметричной относительно прямой g, а прямая g называется осью симметрии фигуры.
СВОЙСТВО ДИАГОНАЛЕЙ ПРЯМОУГОЛЬНИКА.
БИЛЕТ №6
СИММЕТРИЯ ОТНОСИТЕЛЬНО ТОЧКИ.
Симметрия относительно точки
Пусть О — фиксированная точка и X — произвольная точка плоскости (рис. 187). Отложим на продолжении отрезка ОХ за точку О отрезок ОХ’, равный ОХ.
Точка X’ называется симметричной точке X относительно точки О. Точка, симметричная точке О, есть сама точка О. Очевидно, что точка, симметричная точке X’, есть точка X.
Преобразование фигуры F в фигуру F’, при котором каждая ее точка X переходит в точку X’, симметричную относительно данной точки О, называется преобразованием симметрии относительно точки О. При этом фигуры F и F’ называются симметричными относительно точки О (рис. 188).
Если преобразование симметрии относительно точки О переводит фигуру F в себя, то она называется центрально-симметричной, а точка О называется центром симметрии.
ДОКАЖИТЕ, ЧТО ЕСЛИ У ПАРАЛЛЕЛОГРАММА ВСЕ УГЛЫ РАВНЫ, ТО ОН ЯВЛЯЕТСЯ ПРЯМОУГОЛЬНИКОМ.
БИЛЕТ№7.
1.ОПРЕДЕЛЕНИЕ СИНУСА, КОСИНУСА, ТАНГЕНСА И КОСИНУСА ДЛЯ ЛЮБОГО УГЛА ОТ 0° ДО 180°.
Возьмем окружность на плоскости ху с центром в начале координат и радиусом R (рис. 180). Отложим от положительной полуоси X в верхнюю полуплоскость (полуплоскость, где y>0) угол а. Пусть х и у — координаты точки А. Значения sin а, cos а и tg а для острого угла а выражаются через координаты точки А, а именно: Определим теперь значения sin а, cos а и tg а этими формулами для любого угла а. (Для tg а угол а = 90° исключается.)
При таком определении sin 90° = 1, cos 90° = О, sin 180° = О,
cos 180° = — 1, tg 180° = 0.
Считая, что совпадающие лучи образуют угол 0°, будем иметь: sinO° = 0, cosO° = l, tgO° = 0.
Докажем, что для любого угла а, 0°<:а<:180°, sin (180° — а)=sin а, cos (180° — а) = — cos а.
Для угла а ^ 90° tg (180° — а) = — tg а.
Действительно, треугольники ОАВ и ОАВ равны по гипотенузе и острому углу (рис. 181). Из равенства треугольников следует, что АВ=А1В1, т. е. у = у1; ОВ=ОВ1 следовательно, x= —x1. Поэтому разделив почленно равенство sin (180° —а) = sin а
на равенство cos (180° — а)=—cos а, получаем:
Что и требовалось доказать.
СВОЙСТВА ДИАГОНАЛЕЙ РОМБА.
БИЛЕТ№8.
В этом разделе мы рассматриваем геометрический объект параллелограмм. Все элементы параллелограмма наследуются от четырехугольника, поэтому рассматривать их мы не будем. А вот свойства и признаки заслуживают детального рассмотрения. Мы разберем:
- чем признак отличается от свойства;
- рассмотрим основные свойства и признаки, которые изучают в программе 8 класса;
- сформулируем еще два дополнительных свойства, которые получим при решении опорных задач.
2.1 Определение параллелограмма
Чтобы правильно давать определения понятиям в геометрии, нужно не просто их заучивать, а понимать, как они формируются. В этом деле нам хорошо помогают схемы родовых понятий. Давайте посмотрим, что это такое.
Наш учебный модуль называется «Четырехугольники» и четырехугольник является ключевым понятием в этом курсе. Мы можем дать следующее определение четырехугольнику:
Четырёхугольник-это многоугольник, у которого четыре стороны и четыре вершины.
В этом определении родовым понятием будет многоугольник. Теперь дадим определение многоугольнику:
Многоугольником называется простая замкнутая ломаная вместе с частью плоскости, которую она ограничивает.
Ясно, что родовым понятием здесь выступает понятие ломаная. Если мы пойдем далее, то придем к понятию отрезка, а затем к конечным понятиям точка и прямая. Таким же образом мы можем продолжить нашу схему вниз:

Если мы потребуем, чтобы у четырехугольника две стороны были параллельны, а две нет, то мы получим фигуру, которая называется трапецией.
Трапеция – четырехугольник, у которого две стороны параллельны, а две другие — не параллельны.
А в случае, когда все противоположные стороны параллельны, мы имеем дело с параллелограммом.
Параллелограмм – четырехугольник, у которого противоположные стороны параллельны.
2.2 Cвойства параллелограмма
Свойство 1. В параллелограмме противоположные стороны равны и противоположные углы равны.

Докажем это свойство.
Дано: ABCD — параллелограмм.
Доказать: $angle A = angle C, angle B = angle D, AB = CD, AD = BC.$
Доказательство:
При доказательстве свойств любого геометрического объекта всегда вспоминаем его определение. Итак, параллелограмм – четырехугольник, у которого противоположные стороны параллельны. Ключевым моментом здесь выступает параллельность сторон.
Построим секущую ко всем четырем прямым. Такой секущей будет диагональ BD.

Очевидно, что нужно рассмотреть углы, образованные секущей и параллельными прямыми. Так как прямые параллельны, то накрест лежащие углы равны.
Теперь можно увидеть два равных треугольника по второму признаку.
Из равенства треугольников непосредственно следует первое свойство параллелограмма.
Свойство 2. Диагонали параллелограмма точкой пересечения делятся пополам.

Дано: ABCD — параллелограмм.
Доказать: $AO = OC, BO = OD.$
Доказательство:
Логика доказательства здесь такая же, как и в предыдущем свойстве: параллельность сторон и равенство треугольников. Первый шаг доказательства тот же, что у первого свойства.
Вторым шагом мы доказываем равенство треугольников по второму признаку. Обратите внимание, что равенство $BC=AD$ можно принять без доказательства (используя Свойство 1).
Из этого равенства следует, что $AO = OC, BO = OD.$

2.3 Опорная задача №4 (Свойство угла между высотами параллелограмма)

Дано: ABCD — параллелограмм, BK и BM — его высоты, $angle KBM = 60^0$.
Найти: $angle ABK$, $angle A$
Решение:
Приступая к решению этой задачи, нужно иметь ввиду следующее:
высота в параллелограмме перпендикулярна обеим противоположным сторонам
Например, если отрезок $BM$ проведен к стороне $DC$ и является его высотой ($BM perp DC$), то этот же отрезок будет высотой к противположной стороне ($BM perp BA$). Это следует из параллельности сторон $AB parallel DC$.

Далее мы можем найти $angle A$ из прямоугольного $bigtriangleup ABK$: $angle A = 90^0-30^0=60^0$

При решении этой задачи, ценным является свойство, которое мы получаем.
Дополнительное свойство. Угол между высотами параллелограмма, проведенными из его вершины, равен углу при соседней вершине.
2.4 Опорная задача №5 (Свойство биссектрисы параллелограмма)

Биссектриса угла А параллелограмма ABCD пересекает сторону BC в точке L, AD=12 см, AB =10 см.
Найти длину отрезка LC.
Решение:
- $angle 1 = angle 2$ (АК — биссектрисса);
- $angle 2 = angle 3$ (как накрест лежащие углы при $AD parallel BC$ и секущей АL);
- $angle 1 = angle 3$, $bigtriangleup ABL -$ равнобедренный.
Далее несложно найти длину отрезка LC = 2 см.
По ходу решения задачи мы получили свойство:
Дополнительное свойство. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
Определение
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Теорема (первый признак параллелограмма)
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
Доказательство
Пусть в четырехугольнике (ABCD) стороны (AB) и (CD) параллельны и (AB = CD).

Проведём диагональ (AC), разделяющую данный четырехугольник на два равных треугольника: (ABC) и (CDA). Эти треугольники равны по двум сторонам и углу между ними ((AC) – общая сторона, (AB = CD) по условию, (angle 1 = angle 2) как накрест лежащие углы при пересечении параллельных прямых (AB) и (CD) секущей (AC)), поэтому (angle 3 = angle 4). Но углы (3) и (4) накрест лежащие при пересечении прямых (AD) и (BC) секущей (AC), следовательно, (ADparallel BC). Таким образом, в четырехугольнике (ABCD) противоположные стороны попарно параллельны, и, значит, четырехугольник (ABCD) – параллелограмм.
Теорема (второй признак параллелограмма)
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
Доказательство
Проведём диагональ (AC) данного четырехугольника (ABCD), разделяющую его на треугольники (ABC) и (CDA).

Эти треугольники равны по трем сторонам ((AC) – общая, (AB = CD) и (BC = DA) по условию), поэтому (angle 1 = angle 2) – накрест лежащие при (AB) и (CD) и секущей (AC). Отсюда следует, что (ABparallel CD). Так как (AB = CD) и (ABparallel CD), то по первому признаку параллелограмма четырёхугольник (ABCD) – параллелограмм.
Теорема (третий признак параллелограмма)
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Доказательство
Рассмотрим четырехугольник (ABCD), в котором диагонали (AC) и (BD) пересекаются в точке (O) и делятся этой точкой пополам.
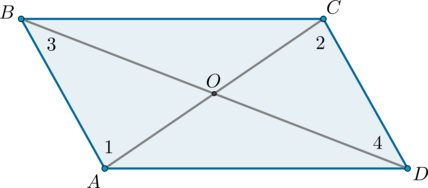
Треугольники (AOB) и (COD) равны по первому признаку равенства треугольников ((AO = OC), (BO = OD) по условию, (angle AOB = angle
COD) как вертикальные углы), поэтому (AB = CD) и (angle 1 = angle
2). Из равенства углов (1) и (2) (накрест лежащие при (AB) и (CD) и секущей (AC)) следует, что (ABparallel CD).
Итак, в четырехугольнике (ABCD) стороны (AB) и (CD) равны и параллельны, значит, по первому признаку параллелограмма четырехугольник (ABCD) – параллелограмм.
Свойства параллелограмма:
1. В параллелограмме противоположные стороны равны и противоположные углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
Свойства биссектрисы параллелограмма:
1. Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
2. Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.
3. Отрезки биссектрис противоположных углов равны и параллельны.
Доказательство
1) Пусть (ABCD) – параллелограмм, (AE) – биссектриса угла (BAD).
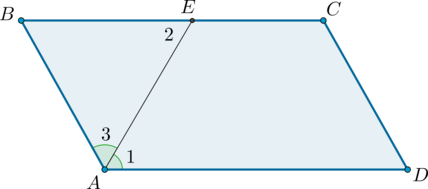
Углы (1) и (2) равны как накрест лежащие при параллельных прямых (AD) и (BC) и секущей (AE). Углы (1) и (3) равны, так как (AE) – биссектриса. В итоге (angle 3 = angle 1 = angle 2), откуда следует, что треугольник (ABE) – равнобедренный.
2) Пусть (ABCD) – параллелограмм, (AN) и (BM)– биссектрисы углов (BAD) и (ABC) соответственно.
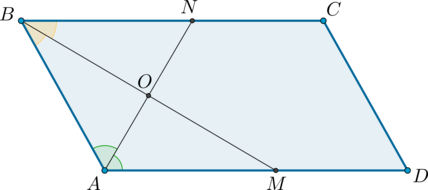
Так как сумма односторонних углов при параллельных прямых и секущей равна (180^{circ}), тогда (angle DAB + angle ABC =
180^{circ}).
Так как (AN) и (BM) – биссектрисы, то (angle BAN + angle ABM =
0,5(angle DAB + angle ABC) = 0,5cdot 180^circ = 90^{circ}), откуда (angle AOB = 180^circ — (angle BAN + angle ABM) =
90^circ).
3. Пусть (AN) и (CM) – биссектрисы углов параллелограмма (ABCD).
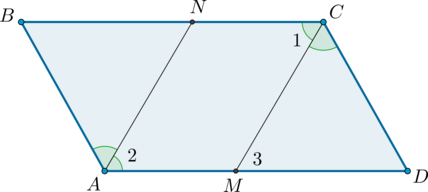
Так как в параллелограмме противоположные углы равны, то (angle 2 =
0,5cdotangle BAD = 0,5cdotangle BCD = angle 1). Кроме того, углы (1) и (3) равны как накрест лежащие при параллельных прямых (AD) и (BC) и секущей (CM), тогда (angle 2 = angle 3), откуда следует, что (ANparallel CM). Кроме того, (AMparallel CN), тогда (ANCM) – параллелограмм, следовательно, (AN = CM).
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
СОДЕРЖАНИЕ СТАТЬИ
1. Параллелограмм
Сложное слово «параллелограмм»? А скрывается за ним очень простая фигура.
Смотри:
 | Параллелограмм – это четырехугольник, противоположные стороны которого попарно параллельны |
Ну, то есть, взяли две параллельные прямые:

Пересекли ещё двумя:

И вот внутри – параллелограмм!
Какие же есть свойства у параллелограмма?
Свойства параллелограмма.
То есть, чем можно пользоваться, если в задаче дан параллелограмм?
На этот вопрос отвечает следующая теорема:
В любом параллелограмме:
- Противоположные стороны равны
- Противоположные углы равны
- Диагонали делятся пополам точкой пересечения
Давай нарисуем все подробно.
Что означает первый пункт теоремы? А то, что если у тебя ЕСТЬ параллелограмм, то непременно
 | и . |
Второй пункт означает, что если ЕСТЬ параллелограмм, то, опять же, непременно:
 | и |
Ну, и наконец, третий пункт означает, что если у тебя ЕСТЬ параллелограмм, то обязательно:
 | и |
Видишь, какое богатство выбора? Что же использовать в задаче? Попробуй ориентироваться на вопрос задачи, или просто пробуй все по очереди – какой-нибудь «ключик» да подойдёт.
А теперь зададимся другим вопросом: а как узнать параллелограмм «в лицо»? Что такое должно случиться с четырехугольником, чтобы мы имели право выдать ему «звание» параллелограмма?
На этот вопрос отвечает несколько признаков параллелограмма.
Признаки параллелограмма.
Внимание! Начинаем.
- Признак 1. Если у четырехугольника две стороны равны и параллельны, то это – параллелограмм.
 | ; — параллелограмм. |
— паралелограмм.
- Признак 2. Если у четырехугольника противоположные стороны равны, то это – параллелограмм.
 | ; – параллелограмм. |
- Признак 3. Если у четырехугольника противоположные углы равны, то это – параллелограмм.
 | ; – параллелограмм. |
- Признак 4. Если у четырехугольника диагонали делятся точкой пересечения пополам, то это – параллелограмм.
 | ; – параллелограмм. |
Обрати внимание: если ты нашёл хотя бы один признак в своей задаче, то у тебя точно параллелограмм, и ты можешь пользоваться всеми свойствами параллелограмма.
Для полной ясности посмотри на схему:

2. Прямоугольник
Думаю, что для тебя вовсе не явится новостью то, что
 | Прямоугольник – четырехугольник, все углы которого прямые. |
Первый вопрос: а является ли прямоугольник параллелограммом?
Конечно, является! Ведь у него и — помнишь, наш признак 3?
А отсюда, конечно же, следует, что у прямоугольника, как и у всякого параллелограмма и , а диагонали точкой пересечения делятся пополам.
Но есть у прямоугольника и одно отличительноесвойство.
Свойство прямоугольника
 | Диагонали прямоугольника равны: . |
Почему это свойство отличительное? Потому что ни у какого другого параллелограмма не бывает равных диагоналей. Сформулируем более чётко.
 | Если у параллелограмма равны диагонали, то это — прямоугольник. |
Обрати внимание: чтобы стать прямоугольником, четырехугольнику нужно сперва стать параллелограммом, а потом уже предъявлять равенство диагоналей.
3. Ромб
 | Ромб – четырехугольник, все стороны которого равны между собой. |
И снова вопрос: ромб – это параллелограмм или нет?
С полным правом – параллелограмм, потому что у него и (вспоминаем наш признак 2).
И снова, раз ромб – параллелограмм, то он обязан обладать всеми свойствами параллелограмма. Это означает, что у ромба противоположные углы равны, противоположные стороны параллельны, а диагонали делятся точкой пересечения пополам.
Но есть и особенные свойства. Формулируем.
Свойства ромба
- Свойство 1. Диагонали ромба перпендикулярны.
 | (если ты забыл, напомню: — значок перпендикулярности) |
- Свойство 2. Диагонали ромба являются биссектрисами его углов.
Посмотри на картинку:

Как и в случае с прямоугольником, свойства эти – отличительные, то есть по каждому из этих свойств можно заключить, что перед нами не просто параллелограмм, а именно ромб.
Признаки ромба
- Признак 1. Если в параллелограмме диагонали перпендикулярны, то это ромб.

- Признак 2. Если в параллелограммехотя бы одна из диагоналей делит пополам оба угла, через которые она проходит, то этот параллелограмм – ромб.

И снова обрати внимание: должен быть не просто четырехугольник, у которого перпендикулярны диагонали, а именно параллелограмм. Убедись:
 | разве это ромб? |
Нет, конечно, хотя его диагонали и перпендикулярны, а диагональ – биссектриса углов и . Но … диагонали не делятся, точкой пересечения пополам, поэтому – НЕ параллелограмм, а значит, и НЕ ромб.
4. Квадрат
 | Квадрат – четырехугольник, у которого все стороны равны между собой, а все углы – прямые. |
То есть квадрат – это прямоугольник и ромб одновременно. Давай посмотрим, что из этого получится.
 | У квадрата угол между диагональю и стороной равен . |
Понятно почему? Квадрат — ромб – биссектриса угла A, который равен . Значит делит (да и тоже) на два угла по .
 | Диагонали квадрата равны, перпендикулярны и делятся точкой пересечения пополам. |
Ну, это совсем ясно: прямоугольник диагонали равны; ромб диагонали перпендикулярны, и вообще – параллелограмм диагонали делятся точкой пересечения пополам.
 | Если сторона квадрата равна , то его диагональ равна . |
Почему? Ну, просто применим теорему Пифагора к .
Значит, .
СРЕДНИЙ УРОВЕНЬ
Свойства четырехугольников. Параллелограмм
Параллелограмм – это четырехугольник, противоположные стороны которого попарно параллельны.

Свойства параллелограмма
Внимание! Слова «свойства параллелограмма» означают, что если у тебя в задаче есть параллелограмм, то всем нижеследующим можно пользоваться.
Итак,
Теорема о свойствах параллелограмма.
В любом параллелограмме:
Давай-ка поймём, почему это всё верно, иными словами ДОКАЖЕМ теорему.
Итак, почему верно 1)?
 | Давай проведём диагональ . Что получится? Два треугольника: и . |
Раз – параллелограмм, то :
- как накрест лежащие
- как накрест лежащие.
Значит, (по II признаку: и — общая.)
Ну вот, а раз , то и – всё! – доказали.
Но кстати! Мы ещё доказали при этом и 2)!
Почему? Но ведь (смотри на картинку), то есть , а именно потому, что .
Осталось только 3).
Для этого всё-таки придётся провести вторую диагональ.
 | Мы уже выяснили, что . Давай снова отметим равные накрест лежащие углы (посмотри и убедись, что все верно). |
И теперь видим, что — по II признаку ( угла и сторона «между» ними).
 | Значит, (напротив углов и ) и (напротив углов и соответственно). |
Свойства доказали! Перейдём к признакам.
Признаки параллелограмма
Напомним, что признак параллелограмма отвечает на вопрос «как узнать?», что фигура является параллелограммом.
Признак 1. Если у четырехугольника две стороны равны и параллельны, то это параллелограмм.
В значках это так:
 | ; – параллелограмм. |
Почему? Хорошо бы понять, почему – этого хватит. Но смотри:
 | по 1 признаку: , — общая и как накрест лежащие при параллельных и и секущей . |
А раз ,
 | то (лежат напротив и соответственно). Но это значит, что ( и — накрест лежащие и оказались равны). |
Ну вот и разобрались, почему признак 1 верен.
Признак 2. Если у четырехугольника противоположные стороны равны, то это – параллелограмм.
 | , – параллелограмм. |
Ну, это ещё легче! Снова проведём диагональ .
 | Теперь просто по трём сторонам. |
А значит:
 | и , то есть – параллелограмм. |
Признак 3. Если у четырёхугольника противоположные углы равны, то это – параллелограмм.
 | , – параллелограмм. |
И тоже несложно. Но …по-другому!
 | (ведь – четырехугольник, а , по условию). |
Значит, . Ух! Но и – внутренние односторонние при секущей !
Поэтому тот факт, что означает, что .
А если посмотришь с другой стороны, то и – внутренние односторонние при секущей ! И поэтому .
Видишь, как здорово?!
Признак 4. Если у четырехугольника диагонали делятся точкой пересечения пополам, то это – параллелограмм.
 | ; – параллелограмм. |
И опять просто:
 | , как вертикальные , , и . |
Точно так же , , и .
Обрати внимание: если ты нашел хотя бы один признак параллелограмма в своей задаче, то у тебя точно параллелограмм, и ты можешь пользоваться всеми свойствами параллелограмма.
Для полной ясности посмотри на схему:

Свойства четырехугольников. Прямоугольник.
 | Прямоугольник – четырехугольник, все углы которого прямые. |
Свойства прямоугольника:
- Прямоугольник – параллелограмм
- Диагонали прямоугольника равны
Пункт 1) совсем очевидный – ведь просто выполнен признак 3 ( )
А пункт 2) – очень важный. Итак, докажем, что
диагонали прямоугольника равны.
 | Раз прямоугольник – это параллелограмм, то . |
А значит, по двум катетам ( и — общий).
Ну вот, раз треугольники и равны, то у них и гипотенузы и тоже равны.
Доказали, что !
И представь себе, равенство диагоналей – отличительное свойство именно прямоугольника среди всех параллелограммов. То есть верно такое утверждение^
Если у параллелограмма равны диагонали, то это прямоугольник.
Давай поймём, почему?
 | – параллелограмм – по условию. – теперь уже по трём сторонам. |
Значит, (имеются в виду углы параллелограмма). Но ещё раз вспомним, что – параллелограмм, и поэтому .
Значит, . Ну и, конечно, из этого следует, что каждый из них по ! Ведь в сумме-то они должны давать !
Вот и доказали, что если у параллелограмма вдруг (!) окажутся равные диагонали, то это точно прямоугольник.
Но! Обрати внимание! Речь идёт о параллелограммах! Не любой четырехугольник с равными диагоналями – прямоугольник, ?



