Каким свойством обладают накрест лежащие углы

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
Стороны угла – лучи, которые образуют угол.
Вершина угла – точка, из которой выходят лучи.

Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.
Важно: в названии буква, обозначающая вершину угла, стоит между двумя буквами, обозначающими точки на сторонах угла. Так, угол, изображенный на рисунке, можно назвать: ∠AOB или ∠BOA, но ни в коем случае не ∠OAB,∠OBA,∠ABO,∠BAO.
Величину угла измеряют в градусах. ∠AOB=24°.
Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.
Или
Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.
OD – биссектриса угла ∠AOB. Она делит этот угол на два равных угла.
∠AOD=∠BOD=∠AOB2
Точка D – произвольная точка на биссектрисе. Она равноудалена от сторон OA и OB угла ∠AOB.
Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.
Свойство: вертикальные углы равны.
Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.
Свойство: сумма смежных углов равна 180°.
Пример:
Пары углов
(1) и (3)
(2) и (4)
называются вертикальными.
По свойству вертикальных углов:
∠COD=∠AOB
∠BOD=∠AOC
Пары углов
(1) и (2)
(2) и (3)
(3) и (4)
(4) и (1)
называются смежными.
По свойству смежных углов:
∠COD+∠DOB=180°∠DOB+∠BOA=180°∠BOA+∠AOC=180°∠AOC+∠COD=180°
Прямая, пересекающая две заданные прямые, называется секущей этих прямых.
Существует пять видов углов, которые образуются при пересечении двух прямых секущей.
Пары углов:
(1) и (5)
(2) и (6)
(3) и (7)
(4) и (8)
называются соответственными.
(Легко запомнить: они соответствуют друг другу, похожи друг на друга).
Пары углов:
(3) и (5)
(4) и (6)
называются внутренними односторонними.
(Легко запомнить: лежат по одну сторону от секущей, между двумя прямыми).
Пары углов:
(1) и (7)
(2) и (8)
называются внешними односторонними.
(Легко запомнить: лежат по одну сторону от секущей по разные стороны от двух прямых).
Пары углов:
(3) и (6)
(4) и (5)
называются внутренними накрест лежащими.
(Легко запомнить: лежат между двумя прямыми, расположены наискосок друг относительно друга).
Пары углов:
(1) и (8)
(2) и (7)
называются внешними накрест лежащими.
(Легко запомнить: лежат по разные стороны от двух прямых, расположены наискосок друг относительно друга).
Если прямые, которые пересекает секущая, параллельны, то углы имеют следующие свойства:
- Соответственные углы равны.
- Внутренние накрест лежащие углы равны.
- Внешние накрест лежащие углы равны.
- Сумма внутренних односторонних углов равна 180°.
- Сумма внешних односторонних углов равна 180°.
Сумма углов произвольного n-угольника вычисляется по формуле:
Sn=180°⋅(n−2)
где n – это количество углов в n-угольнике.
Пользуясь этой формулой, можно вычислить сумму углов для произвольного n-угольника.
Сумма углов треугольника: S3=180°⋅(3−2)=180°
Сумма углов четырехугольника: S4=180°⋅(4−2)=360°
Сумма углов пятиугольника: S5=180°⋅(5−2)=540°
Так можно продолжать до бесконечности.
Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.
На рисунках изображены примеры правильных многоугольников:
Чтобы найти величину угла правильного n-угольника, необходимо сумму углов этого многоугольника разделить на количество углов.
αn=180°⋅(n−2)n
Модуль геометрия: задания, связанные с углами
Скачать домашнее задание к уроку 2.
Евгения Кукушкина
Ученик
(214)
5 лет назад
1.Две прямые называют параллельными, если они не пересаются
2.прямая… называют секущей прямых.. и..
3.соответсвенные накрест лежащие односторонние
9.через точку не лежащию на данной прямой проходит только одна прямая параллельная данной
Юля Попугаева
Профи
(555)
5 лет назад
1) отрезки которые не пересекаются называются параллельными
2) секущая-это линия, пересекающая 2 параллельные прямые, углы — накрестлежащие, соответственные, односторонние
3,4,5,6 — это есть скорее всего в учебнике
7) аксиомы-это 100% верное утверждение, которое не нуждается в доказательстве, к примеру «через точку, не лежащую на данной прямой, можно провести прямую, параллельную ей, притом только одну ( я не уверена, что она так звучит, но что-то похожее)
остальное должно быть в учебнике или в интернете, своими словами сложно написать
Елена Ткачёва
Знаток
(445)
5 лет назад
1.Параллельными прямыми называются прямые, которые лежат в одной плоскости и либо совпадают, либо не пересекаются.
2.прямая пересекающая одновременно две (три) другие прямые в двух точках (в трех)
3.Пусть при пересечении прямых а и с секущей АВ накрест лежащие углы 1 и 2 равны. Если углы 1 и 2 прямые, то прямые а и с перпендикулярны к прямой АВ и следовательно параллельны. Доп. Построен. Проведем перпендикуляр ОН из середины отрезка АВ к прямой а. На прямой с от точки В отложим отрезок ВН1, равный отрезку АН и проведем отрезок ОН1. Треугольники ОНА и ОН1В равны по двум сторонам и углу между ними. Поэтому угол 3=4 и 5=6. Из равенства 3=4, точки Н, Р и Н1 лежат на одной прямой, а из равенства 5=6 : угол 6 прямой. прямые а и с перпендикулярны к прямой НН1, поэтому они параллельны.
5.так как секущая для двух параллельных идет под разным всвязи с этим образуется 2 угла градус одного из них меньше градуса второго
6.С помощью двух треугольников. Один трегольник жестко удерживается на бумаге. Второй треугольник одной из своих сторон прикладывается к одной из сторон первого треугольника и может скользить вдоль нее, а параллельные прямые получаются черчением вдоль другой стороны второго треугольника.
7.Аксиомы — утверждения, не требующие доказательства. Например, через две точки можно провести ТОЛЬКО одну прямую — это аксиома
8.Это одна из аксиом… Через данную точку, не лежащую на данной прямой, проходит прямая, параллельная данной, и только одна.
9.АКСИОМА О ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ: через данную точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
10.Утверждения, которые выводятся непосредственно из аксиом или теорем, называются следствиями.
Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Доказательство: Пусть прямые a и параллельны и прямая с пересекает прямую а в точке М. Докажем, что прямая с пересекает и прямую b.Если бы прямая с не пересекала прямую b, то через точку М проходили бы две прямые (прямые а и с), параллельные прямой b.Но это противоречит аксиоме параллельных прямых, и, значит, прямая с пересекает прямую b.
11. Если две прямые параллельны третьей прямой, то они параллельны.
Док-во: Пусть прямые a и b параллельны прямой с. Докажем, что a||b. Допустим, что прямые a и b не параллельны, т. е. пересекаются в некоторой точке М. Тогда через точку М проходят две прямые, параллельные прямой с.
Но это противоречит аксиоме параллельных прямых (через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной). Поэтому наше предположение неверно, а значит, прямые a и b параллельны.
12.это теорема, в которой заключение является условием, а условиие -заключением.
например если треугольник равнобедренный, то углы пи основании равны. и обратно если углы при основании равны, то треугольник равнобедренный.
13.пусть при пересечении прямых а и b секущей АВ накрест лежащие углы = если накрест лежащие углы прямые то прямые а и b перпендикулярны к прямой АВ и следовательно параллельны
14.Допустим первая параллельная прямая А, а вторая В, прямая перпендикулярная прямой А будет С. Рассмотрим прямые А||В и С-секущая: Т. к. С перпендикулярна А то по свойству, что соответственные углы равны получаем, что С перпендикулярна В. Доказано.
15.а) Пусь прямые параллельные А и В пересечены секуещей С. Докажем, что соотственные углы, например 1 и 2 равны. Так как А параллельна В, то накрест лежащие углы 1 и 3 равны. Углы 2 и 3 равны как вертикальные. Из равенств угол 1 = 3 и 2 = 3 следует что, угол 1 = 2.
б) Пусть прямые параллельные А и В пересечены секущей С. Докажем, например что угол 1+4=180 градусов, так как А параллельна В, то соответственные углы 1 и 2 равны. Углы 2 и 4 смежные, поэтому угол 2 +4 = 180 градусов.
Максим Зык
Знаток
(255)
3 года назад
ввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввввоооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооотттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттттт
это вернооооооооооооооооооооооооо ты сказалллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллл
спасибо
Валерия Павлова
Ученик
(120)
3 года назад
5.Пусть при пересечении прямых а и b секущей c сумма односторонних углов равна 180. Т. к. эти углы 3 и 4 смежные, то 3+4=180. Из этих двух равенств следует, что накрест лежащие углы 1 и 3 равны, поэтому прямые параллельны.
Признаки параллельности двух прямых
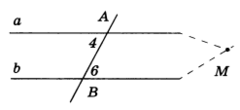
Рис.1
Теорема 1. Если при пересечении двух прямых секущей:
накрест лежащие углы равны, или
соответственные углы равны, или
сумма односторонних углов равна 180°, то
прямые параллельны (рис.1).
Доказательство. Ограничимся доказательством случая 1.
Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны. Например, ∠ 4 = ∠ 6. Докажем, что а || b.
Предположим, что прямые а и b не параллельны. Тогда они пересекаются в некоторой точке М и, следовательно, один из углов 4 или 6 будет внешним углом треугольника АВМ. Пусть для определенности ∠ 4 — внешний угол треугольника АВМ, а ∠ 6 — внутренний. Из теоремы о внешнем угле треугольника следует, что ∠ 4 больше ∠ 6, а это противоречит условию, значит, прямые а и 6 не могут пересекаться, поэтому они параллельны.
Следствие 1. Две различные прямые на плоскости, перпендикулярные одной и той же прямой, параллельны (рис.2).
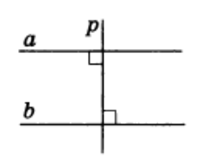
Рис.2
Замечание. Способ, которым мы только что доказали случай 1 теоремы 1, называется методом доказательства от противного или приведением к нелепости. Первое название этот способ получил потому, что в начале рассуждения делается предположение, противное (противоположное)
тому, что требуется доказать. Приведением к нелепости он называется вследствие того, что, рассуждая на основании сделанного предположения, мы приходим к нелепому выводу (к абсурду). Получение такого вывода заставляет нас отвергнуть сделанное вначале допущение и принять то, которое требовалось доказать.

Задача 1. Построить прямую, проходящую через данную точку М и параллельную данной прямой а, не проходящей через точку М.
Решение. Проводим через точку М прямую р перпендикулярно прямой а (рис. 3).
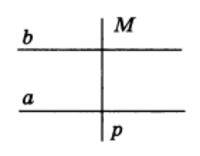
Рис.3
Затем проводим через точку М прямую b
перпендикулярно прямой р. Прямая b
параллельна прямой а согласно следствию из
теоремы 1.
Из рассмотренной задачи следует важный вывод:
через точку, не лежащую на данной прямой, всегда можно провести прямую, параллельную данной.
Основное свойство параллельных прямых состоит в следующем.
Аксиома параллельных прямых. Через данную точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Рассмотрим некоторые свойства параллельных прямых, которые следуют из этой аксиомы.
1) Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую (рис.4).
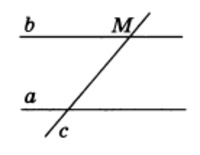
Рис.4
2) Если две различные прямые параллельны третьей прямой, то они параллельны (рис.5).

Рис.5
Справедлива и следующая теорема.
Теорема 2. Если две параллельные прямые пересечены секущей, то:
накрест лежащие углы равны;
соответственные углы равны;
сумма односторонних углов равна 180°.
Следствие 2. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой (см. рис.2).

Рис.2
Замечание. Теорема 2 называется обратной теореме 1. Заключение теоремы 1 является условием теоремы 2. А условие теоремы 1 является заключением теоремы 2. Не всякая теорема имеет обратную, т. е. если данная теорема верна, то обратная теорема может быть неверна.
Поясним это на примере теоремы о вертикальных углах. Эту теорему можно сформулировать так: если два угла вертикальные, то они равны. Обратная ей теорема была бы такой: если два угла равны, то они вертикальные. А это, конечно, неверно. Два равных угла вовсе не обязаны быть вертикальными.
Пример 1. Две параллельные прямые пересечены третьей. Известно, что разность двух внутренних односторонних углов равна 30°. Найти эти углы.
Решение. Пусть условию отвечает рисунок 6.
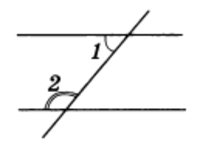
Рис.6
Углы 1 и 2 внутренние односторонние, их сумма равна 180°, т. е.
∠ l + ∠ 2 = 180°. (1)
Обозначим градусную меру угла 1 через х. По условию ∠ 2 — х = 30°, или ∠ 2 = 30° + x.
Подставим в равенство (1) значения углов 1 и 2, получим
х + 30° + х = 180°.
Решая это уравнение, получим х = 75°, т. е.
∠ 1 = 75°, a ∠ 2 = 180° — 75° = 105°.
Пример 2. Две параллельные прямые пересечены третьей. Известно, что сумма двух внутренних накрест лежащих углов равна 150°. Чему равны эти углы и остальные шесть?
Решение. Пусть условию задачи соответствует рисунок 7.
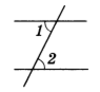
Рис.7
Углы 1 и 2 внутренние накрест лежащие, следовательно, они равны. Сумма этих углов по условию задачи равна 150°, тогда ∠ 1 = ∠ 2 = 75°.
Найдем остальные углы (рис. 8):
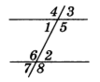
Рис.8
∠ 1 = ∠ 3 = 75° и ∠ 2 = ∠ 7 = 75° (вертикальные). Углы 4 и 5, 6 и 8 равны как вертикальные, a ∠ 5 = ∠ 6 как внутренние накрест лежащие. Все перечисленные углы 4, 5, 6 и 8 равны между собой и равны по 105°, так как ∠ 4 + ∠ 3 = 180°, a ∠ 4 = 180° — ∠ 3.
Получили четыре угла по 75°, четыре угла по 105°.

