Каким свойством обладают графики обратных функций
Определение и свойства
Определение обратной функции
Пусть функция имеет область определения X и множество значений Y. И пусть она обладает свойством:
для всех .
Тогда для любого элемента из множества Y можно поставить в соответствие только один элемент множества X, для которого . Такое соответствие определяет функцию, которая называется обратной функцией к . Обратная функция обозначается так:
.
Из определения следует, что
;
для всех ;
для всех .
Лемма о взаимной монотонности прямой и обратной функций
Если функция строго возрастает (убывает), то существует обратная функция , которая также строго возрастает (убывает).
Доказательство ⇓
Свойство о симметрии графиков прямой и обратной функций
Графики прямой и обратной функций симметричны относительно прямой .
Доказательство ⇓
Теорема о существовании и непрерывности обратной функции на отрезке
Пусть функция непрерывна и строго возрастает (убывает) на отрезке . Тогда на отрезке определена и непрерывна обратная функция , которая строго возрастает (убывает).
Доказательство ⇓
Для возрастающей функции . Для убывающей – .
Теорема о существовании и непрерывности обратной функции на интервале
Пусть функция непрерывна и строго возрастает (убывает) на открытом конечном или бесконечном интервале . Тогда на интервале определена и непрерывна обратная функция , которая строго возрастает (убывает).
Доказательство ⇓
Для возрастающей функции .
Для убывающей: .
Аналогичным образом можно сформулировать теорему о существовании и непрерывности обратной функции на полуинтервале.
Если функция непрерывна и строго возрастает (убывает) на полуинтервале или , то на полуинтервале или определена обратная функция , которая строго возрастает (убывает). Здесь .
Если строго возрастает, то интервалам и соответствуют интервалы и . Если строго убывает, то интервалам и соответствуют интервалы и .
Эта теорема доказывается тем же способом, что и теорема о существовании и непрерывности обратной функции на интервале.
Примеры обратных функций
Арксинус
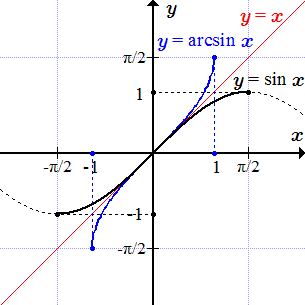
Графики y = sin x и обратной функции y = arcsin x.
Рассмотрим тригонометрическую функцию синус: . Она определена и непрерывна для всех значений аргумента , но не является монотонной. Однако, если сузить область определения, то можно выделить монотонные участки. Так, на отрезке , функция определена, непрерывна, строго возрастает и принимает значения от –1 до +1. Поэтому имеет на нем обратную функцию, которую называют арксинусом. Арксинус имеет область определения и множество значений .
Логарифм
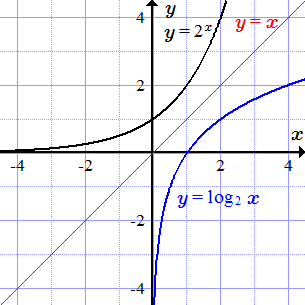
Графики y = 2x и обратной функции y = log2 x.
Показательная функция определена, непрерывна и строго возрастает при всех значений аргумента . Множеством ее значений является открытый интервал . Обратной функцией является логарифм по основанию два. Он имеет область определения и множество значений .
Квадратный корень
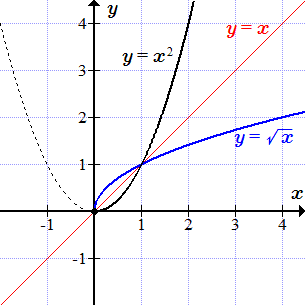
Графики y = x2 и обратной функции .
Степенная функция определена и непрерывна для всех . Множеством ее значений является полуинтервал . Но она не является монотонной при всех значений аргумента. Однако, на полуинтервале она непрерывна и строго монотонно возрастает. Поэтому если, в качестве области определения, взять множество , то существует обратная функция, которая называется квадратным корнем. Обратная функция имеет область определения и множество значений .
Пример. Доказательство существования и единственности корня степени n
Докажите, что уравнение , где n – натуральное, – действительное неотрицательное число, имеет единственное решение на множестве действительных чисел, . Это решение называется корнем степени n из числа a. То есть нужно показать, что любое неотрицательное число имеет единственный корень степени n.
Решение
Рассмотрим функцию от переменной x:
(П1) .
Докажем, что она непрерывна.
Используя определение непрерывности, покажем, что
.
Применяем формулу бинома Ньютона:
(П2)
.
Применим арифметические свойства пределов функции. Поскольку , то отлично от нуля только первое слагаемое:
.
Непрерывность доказана.
Докажем, что функция (П1) строго возрастает при .
Возьмем произвольные числа , связанные неравенствами:
, , .
Нам нужно показать, что . Введем переменные . Тогда . Поскольку , то из (П2) видно, что . Или
.
Строгое возрастание доказано.
Найдем множество значений функции при .
В точке , .
Найдем предел .
Для этого применим неравенство Бернулли. При имеем:
.
Поскольку , то и .
Применяя свойство неравенств бесконечно больших функций находим, что .
Таким образом, , .
Согласно теореме об обратной функции, на интервале определена и непрерывна обратная функция . То есть для любого существует единственное , удовлетворяющее уравнению . Поскольку у нас , то это означает, что для любого , уравнение имеет единственное решение, которое называют корнем степени n из числа x:
.
Доказательства свойств и теорем
Доказательство леммы о взаимной монотонности прямой и обратной функций
Формулировка ⇑
Пусть функция имеет область определения X и множество значений Y. Докажем, что она имеет обратную функцию. Исходя из определения ⇑, нам нужно доказать, что
для всех .
Допустим противное. Пусть существуют числа , так что . Пусть при этом . Иначе, поменяем обозначения, чтобы было . Тогда, в силу строгой монотонности f, должно выполняться одно из неравенств:
если f строго возрастает;
если f строго убывает.
То есть . Возникло противоречие. Следовательно, имеет обратную функцию .
Пусть функция строго возрастает. Докажем, что и обратная функция также строго возрастает. Введем обозначения:
. То есть нам нужно доказать, что если , то .
Допустим противное. Пусть , но .
Если , то . Этот случай отпадает.
Пусть . Тогда, в силу строгого возрастания функции , , или . Возникло противоречие. Поэтому возможен только случай .
Для строго возрастающей функции лемма доказана. Аналогичным образом можно доказать эту лемму и для строго убывающей функции.
Доказательство свойства о симметрии графиков прямой и обратной функций
Формулировка ⇑
Пусть – произвольная точка графика прямой функции :
(2.1) .
Покажем, что точка , симметричная точке A относительно прямой , принадлежит графику обратной функции :
.
Из определения обратной функции следует, что
(2.2) .
Таким образом, нам нужно показать (2.2).
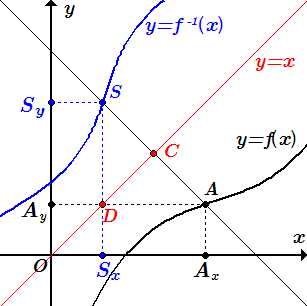
График обратной функции y = f –1(x) симметричен графику прямой функции y = f(x) относительно прямой y = x.
Из точек A и S опустим перпендикуляры на оси координат. Тогда
, .
Через точку A проводим прямую, перпендикулярную прямой . Пусть прямые пересекаются в точке C. На прямой строим точку S так, чтобы . Тогда точка S будет симметрична точке A относительно прямой .
Рассмотрим треугольники и . Они имеют две равные по длине стороны: и , и равные углы между ними: . Поэтому они конгруэнтны. Тогда
.
Рассмотрим треугольник . Поскольку , то
.
Тоже самое относится к треугольнику :
.
Тогда
.
Теперь находим и :
;
.
Итак, уравнение (2.2):
(2.2)
выполняется, поскольку , и выполняется (2.1):
(2.1) .
Так как мы выбрали точку A произвольно, то это относится ко всем точкам графика :
все точки графика функции , симметрично отраженные относительно прямой , принадлежат графику обратной функции .
Далее мы можем поменять и местами. В результате получим, что
все точки графика функции , симметрично отраженные относительно прямой , принадлежат графику функции .
Отсюда следует, что графики функций и симметричны относительно прямой .
Свойство доказано.
Доказательство теоремы о существовании и непрерывности обратной функции на отрезке
Формулировка ⇑
Пусть обозначает область определения функции – отрезок .
1. Покажем, что множеством значений функции является отрезок :
,
где .
Действительно, поскольку функция непрерывна на отрезке , то по теореме Вейерштрасса она достигает на нем минимума и максимума . Тогда по теореме Больцано – Коши функция принимает все значения из отрезка . То есть для любого существует , для которого . Поскольку и есть минимум и максимум, то функция принимает на отрезке только значения из множества .
2. Поскольку функция строго монотонна, то согласно вышеприведенной лемме ⇑, существует обратная функция , которая также строго монотонна (возрастает, если возрастает ; и убывает, если убывает ). Областью определения обратной функции является множество , а множеством значений – множество .
3. Теперь докажем, что обратная функция непрерывна.
3.1. Пусть есть произвольная внутренняя точка отрезка : . Докажем, что обратная функция непрерывна в этой точке.
Пусть ей соответствует точка . Поскольку обратная функция строго монотонна, то есть внутренняя точка отрезка :
.
Согласно определению непрерывности нам нужно доказать, что для любого имеется такая функция , при которой
(3.1) для всех .
Заметим, что мы можем взять сколь угодно малым. Действительно, если мы нашли такую функцию , при которой неравенства (3.1) выполняются при достаточно малых значениях , то они будут автоматически выполняться и при любых больших значениях , если положить при .
Возьмем настолько малым, чтобы точки и принадлежали отрезку :
.
Введем и упорядочим обозначения:
.
Преобразуем первое неравенство (3.1):
(3.1) для всех .
;
;
;
(3.2) .
Поскольку строго монотонна, то отсюда следует, что
(3.3.1) , если возрастает;
(3.3.2) , если убывает.
Поскольку обратная функция также строго монотонна, то из неравенств (3.3) следуют неравенства (3.2).
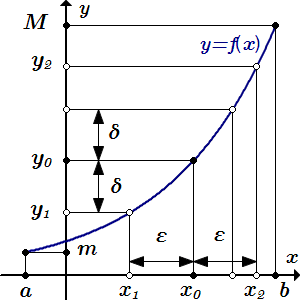
Для любого ε > 0 существует δ, так что |f -1(y) – f -1(y0)| < ε для всех |y – y0| < δ.
Неравенства (3.3) определяют открытый интервал, концы которого удалены от точки на расстояния и . Пусть есть наименьшее из этих расстояний:
.
В силу строгой монотонности , , . Поэтому и . Тогда интервал будет лежать в интервале, определяемом неравенствами (3.3). И для всех значений , принадлежащих ему будут выполняться неравенства (3.2).
Итак, мы нашли, что для достаточно малого , существует , так что
при .
Теперь изменим обозначения.
Для достаточно малого , существует такое , так что
при .
Это означает, что обратная функция непрерывна во внутренних точках .
3.2. Теперь рассмотрим концы области определения. Здесь все рассуждения остаются теми же самыми. Только нужно рассматривать односторонние окрестности этих точек. Вместо точки будет или , а вместо точки – или .
Так, для возрастающей функции , . Обратная функция непрерывна в точке , поскольку для любого достаточно малого имеется , так что
при .
Обратная функция непрерывна в точке , поскольку для любого достаточно малого имеется , так что
при .
Для убывающей функции , .
Обратная функция непрерывна в точке , поскольку для любого достаточно малого имеется , так что
при .
Обратная функция непрерывна в точке , поскольку для любого достаточно малого имеется , так что
при .
Теорема доказана.
Доказательство теоремы о существовании и непрерывности обратной функции на интервале
Формулировка ⇑
Пусть обозначает область определения функции – открытый интервал . Пусть – множество ее значений. Согласно приведенной выше лемме ⇑, существует обратная функция , которая имеет область определения , множество значений и является строго монотонной (возрастает если возрастает и убывает если убывает ). Нам осталось доказать, что
1) множеством является открытый интервал , и что
2) обратная функция непрерывна на нем.
Здесь .
1. Покажем, что множеством значений функции является открытый интервал :
.
Как и всякое непустое множество, элементы которого имеют операцию сравнения, множество значений функции имеет нижнюю и верхнюю грани:
.
Здесь и могут быть конечными числами или символами и .
1.1. Покажем, что точки и не принадлежат множеству значений функции. То есть множество значений не может быть отрезком .
Если или является бесконечно удаленной точкой: или , то такая точка не является элементом множества. Поэтому она не может принадлежать множеству значений.
Пусть (или ) является конечным числом. Допустим противное. Пусть точка (или ) принадлежит множеству значений функции . То есть существует такое , для которого (или ). Возьмем точки и , удовлетворяющие неравенствам:
.
Поскольку функция строго монотонна, то
, если f возрастает;
, если f убывает.
То есть мы нашли точку, значение функции в которой меньше (больше ). Но это противоречит определению нижней (верхней) грани, согласно которому
для всех .
Поэтому точки и не могут принадлежать множеству значений функции .
1.2. Теперь покажем, что множество значений является интервалом , а не объединением интервалов и точек. То есть для любой точки существует , для которого .
Согласно определениям нижней и верхней граней, в любой окрестности точек и содержится хотя бы один элемент множества . Пусть – произвольное число, принадлежащее интервалу : . Тогда для окрестности существует , для которого
.
Для окрестности существует , для которого
.
Поскольку и , то . Тогда
(4.1.1) если возрастает;
(4.1.2) если убывает.
Неравенства (4.1) легко доказать от противного. Но можно воспользоваться леммой ⇑, согласно которой на множестве существует обратная функция , которая строго возрастает, если возрастает и строго убывает, если убывает . Тогда сразу получаем неравенства (4.1).
Итак, мы имеем отрезок , где если возрастает;
если убывает.
На концах отрезка функция принимает значения и . Поскольку , то по теореме Больцано – Коши, существует точка , для которой .
Поскольку , то тем самым мы показали, что для любого существует , для которого . Это означает, что множеством значений функции является открытый интервал .
2. Теперь покажем, что обратная функция непрерывна в произвольной точке интервала : . Для этого применим предыдущую теорему ⇑ к отрезку . Поскольку , то обратная функция непрерывна на отрезке , в том числе и в точке .
Теорема доказана.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано: 27-10-2018 Изменено: 23-11-2018
Пусть множества $X$ и $Y$ включены в множество действительных чисел. Введем понятие обратимой функции.
Определение 1
Функция $f:Xto Y$ отображающая множество $X$ в множество $Y$ называется обратимой, если для любых элементов $x_1,x_2in X$ из того что $x_1ne x_2$ следует, что $f(x_1)ne f(x_2)$.
Теперь мы можем ввести понятие обратной функции.
Определение 2
Пусть функция $f:Xto Y$ отображающая множество $X$ в множество $Y$ обратима. Тогда функция $f^{-1}:Yto X$ отображающая множество $Y$ в множество $X$ определяемая условием $f^{-1}left(yright)=x$ называется обратной для $f(x)$.
Сформулируем теорему:
Теорема 1
Пусть функция $y=f(x)$ определена, монотонно возрастает (убывает) и непрерывна в некотором промежутке $X$. Тогда в соответствующем промежутке $Y$ значений этой функции у нее существует обратная функция, которая также монотонно возрастает (убывает) и непрерывна на промежутке $Y$.
Введем теперь, непосредственно, понятие взаимно обратных функций.
Определение 3
В рамках определения 2, функции $f(x)$ и $f^{-1}left(yright)$ называются взаимно обратными функциями.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Свойства взаимно обратных функций
Пусть функции $y=f(x)$ и $x=g(y)$ взаимно обратные, тогда
$y=f(gleft(yright))$ и $x=g(f(x))$
Область определения функции $y=f(x)$ равна области значения функции$ x=g(y)$. А область определения функции $x=g(y)$ равна области значения функции$ y=f(x)$.
Графики функций $y=f(x)$ и $x=g(y)$ симметричны относительно прямой $y=x$.
Если одна из функций возрастает (убывает), то и другая функция возрастает (убывает).
Нахождение обратной функции
Решается уравнение $y=f(x)$ относительно переменной $x$.
Из полученных корней находят те, которые принадлежат промежутку $X$.
Найденные $x$ ставят в соответствия числу $y$.
Пример 1
Найти обратную функцию, для функции $y=x^2$ на промежутке $X=[-1,0]$
Так как эта функция убывает и непрерывна на промежутке $X$, то на промежутке $Y=[0,1]$, которая также убывает и непрерывна на этом промежутке (теорема 1).
Вычислим $x$:
[y=x^2] [x=pm sqrt{y}]
Выбираем подходящие $x$:
[x=-sqrt{y}]
Ответ: обратная функция $y=-sqrt{x}$.
Задачи на нахождение обратных функций
В этой части рассмотрим обратные функции для некоторых элементарных функций. Задачи будем решать по схеме, данной выше.
Пример 2
Найти обратную функцию для функции $y=x+4$
Решение.
Так как функция возрастает и непрерывна на всей области определения, то, по теореме 1, она имеет на ней обратную непрерывную и возрастающую функцию.
Найдем $x$ из уравнения $y=x+4$:
[y=x+4] [x=y-4]
Находим подходящие значения $x$
Значение в нашем случае подходит (так как область определения — все числа)
Переопределим переменные, получим, что обратная функция имеет вид
[y=x-4]
Пример 3
Найти обратную функцию для функции $y=x^3$
Решение.
Так как функция возрастает и непрерывна на всей области определения, то, по теореме 1, она имеет на ней обратную непрерывную и возрастающую функцию.
Найдем $x$ из уравнения $y=x^3$:
[y=x^3] [x=sqrt[3]{y}]
Находим подходящие значения $x$
Значение в нашем случае подходит (так как область определения — все числа)
Переопределим переменные, получим, что обратная функция имеет вид
[y=sqrt[3]{x}]
Пример 4
Найти обратную функцию для функции $y=cosx$ на промежутке $[0,pi ]$
Решение.
Рассмотрим на множестве $X=left[0,pi right]$ функцию $y=cosx$. Она непрерывна и убывает на множестве $X$ и отображает множество $X=left[0,pi right]$ на множество $Y=[-1,1]$, поэтому по теореме о существовании обратной непрерывной монотонной функции у функции $y=cosx$ в множестве $Y$ существует обратная функция, которая также непрерывна и возрастает в множестве $Y=[-1,1]$ и отображает множество $[-1,1]$ на множество $left[0,pi right]$.
Найдем $x$ из уравнения $y=cosx$:
[y=cosx] [x=pm arccosy+2pi n,nin Z]
Находим подходящие значения $x$
[x=arccosy]
Переопределим переменные, получим, что обратная функция имеет вид
[y=arccosx]
Пример 5
Найти обратную функцию для функции $y=tgx$ на промежутке $left(-frac{pi }{2},frac{pi }{2}right)$.
Решение.
Рассмотрим на множестве $X=left(-frac{pi }{2},frac{pi }{2}right)$ функцию $y=tgx$. Она непрерывна и возрастает на множестве $X$ и отображает множество $X=left(-frac{pi }{2},frac{pi }{2}right)$ на множество $Y=R$, поэтому по теореме о существовании обратной непрерывной монотонной функции у функции $y=tgx$ в множестве $Y$ существует обратная функция, которая также непрерывна и возрастает в множестве $Y=R$ и отображает множество $R$ на множество $left(-frac{pi }{2},frac{pi }{2}right)$
Найдем $x$ из уравнения $y=tgx$:
[y=tgx] [x=arctgy+pi n,nin Z]
Находим подходящие значения $x$
[x=arctgy]
Переопределим переменные, получим, что обратная функция имеет вид
[y=arctgx]
Предмет: алгебра Класс: 10 Автор учебника Мордкович А.Г.
Тема урока: Обратная функция
Тип урока: урок открытия новых знаний
Учитель: Лосинская Наталья Викторовна
всего часов на тему: 2 номер урока в теме: 1
Цель урока: организация условий достижения учащимися образовательных результатов по теме «Обратная функция»
применение знаний и умений,
приобретение учебной информации,
контроль усвоения теории.
Задачи урока: освоение учащимися предметного (теоретического и практического) содержания по теме «Обратная функция»:
знание определений обратимой и обратных функций; теорем об обратимости монотонной функции, об одинаковой монотонности функции и обратной функции,
умение применять знания теории к решению практических задач,
сформировать способность к использованию свойств обратных функций к дальнейшему изучению функциональной линии (пропедевтика, в частности к тригонометрическим функциям),
Методы обучения: активные методы обучения: фронтальная беседа, работа в группе, в паре.
Необходимое оборудование: проектор, презентация, раздаточный материал
Ход урока.
Организационный этап.
Приветствие учителя, проверка готовности обучающихся к уроку.
– Добрый день, ребята, я желаю вам успеха на уроке, пожелайте успеха друг другу, и начнём работать.
Мотивация к учебной деятельности.
– С какой функцией мы работаем? (С числовой.)
– Дайте определение числовой функции?
– Что называется графиком функции?
– Какие задания, связанные с числовыми функциями мы умеем выполнять? (исследовать функцию на монотонность; исследовать функцию на ограниченность; определять и доказывать четность функции; строить и читать график функции).
Для учащихся на интерактивной доске демонстрируется график функции (рис. 1). Учителем формулируется задание – рассмотреть график функции и перечислить изученные свойства функции. Учащиеся перечисляют свойства функции в соответствии со схемой исследования.
Свойства функции:
D(f) = [-4;), E(y) = [0;).
Ни четная, ни нечетная, непериодическая, непрерывная, ограничена снизу.
y=0 при х=0.
y>0 при на [-4;0) и на (0;).
Возрастает на (-2;-1) и на (0;);
убывает на (-4;-2) и на (-1;0).yнаиб- не существует; yнаим=0 при х=0.
xmax= -1 ,ymax = 2; xmin = -2, ymin = 1; xmin = 0, ymin = 0.
Рис. 1 8. Выпукла вниз на (-4;-1), выпукла вверх на (1;+), невыпуклая на [-1;1].
Постановка цели перед учащимися:
– Сегодня на уроке мы продолжим работу с «Числовыми функциями» и познакомимся еще с одним свойством функции – обратимостью. Для осмысленного изучения нового материала учитель предлагает ребятам познакомиться с основными вопросами, на которые учащиеся должны дать ответ по окончании урока. Вопросы в виде раздаточного материала есть у каждого ученика (раздается до урока).
Вопросы:
1. Какая функция называется обратимой?
2. Какая функция называется обратной?
3. Как связаны между собой области определения и множества значений прямой и обратной функций?
4. Сформулируйте достаточное условие обратимости функции.
5. Функция обратная возрастающей является убывающей или возрастающей?
6. Как расположены графики взаимно обратных функций?
Пример № 1. Представим себе такую ситуацию. Вы пытаетесь вспомнить, когда произошло какое-то событие. Вы не можете вспомнить, когда именно, в каком году оно произошло. Однако помните, что в это время вам задали выучить наизусть стихотворение Пушкина «Я помню чудное мгновение». Эта информация оказывается полезной: теперь вы можете вспомнить, как была устроена программа по литературе, когда вы проходили и учили эти стихи, а можете и заглянуть в учебник. Так, при помощи косвенного обстоятельства вы восстанавливаете дату интересующего вас события.
Что произошло в рассказанной истории с точки зрения функции? Вам была известна функция – литературное произведение в школьной программе в зависимости от времени обучения. Эту функцию вы знаете или, по крайней мере, можете восстановить с помощью учебника. Вы не знали, какое значение аргумента (момент времени) вам нужно, но знали значение функции (литературное произведение), соответствующее этому моменту. Итак, по значению функции мы восстановили её аргумент.
Такие действия мы производим в жизни часто, совершенно не думая о функциях. Как же описать то, что мы сделали, на языке функций, избавившись от лишних подробностей?
Итак, пусть функция f(x) в соответствие каждому элементу множества X (его называют областью определения) ставит элемент множества Y (его называют областью значений). Скажем, если речь идёт о телефонной книге, то X – множество людей, чьи телефоны там записаны, Y – множество телефонных номеров из этой книги. Мы же построили обратную функцию – функцию, которая по номеру телефона восстанавливает имя. Так, если мы говорим о телефонной книге в мобильном телефоне, если мы наберём номер, содержащийся в ней, то на экране высветится имя обладателя этого номера. Мы будем говорить, что g(y) обратная к f (x) функция, если g(y)=x тогда и только тогда, когда f(x)=y.
Для обратной функции обычно используют обозначение f -1(x). Не нужно путать это обозначение с возведением в степень!
Задача.

Рассмотрим ещё одну задачу.
Задача.

Давайте назовём первую задачу прямой, тогда вторая задача будет обратной к первой.
Давайте рассмотрим с вами ещё одну задачу.
Задача.

Назовём функцию v(t) обратимой функцией, а t(v) – обратной функцией.
Для дальнейшей работы нам нужно повторить некоторые моменты, выполнив задания.
Актуализация знаний и фиксация затруднения в пробном действии.
Работа в группах:
Найдите значение аргумента х, если значение функции у= равно а) 2; б)
Найдите единственное значение аргумента х, если значение функции y= равно 4
4. Выявление места и причины затруднения.
— Какие возникли проблемы?
— А в чем возникли сомнения? У любой ли функции существует обратная?
Уч-ся: Есть такие значения функции, которые функция принимает более чем в одной точке т.е. есть необратимые функции
5. Построение проекта выхода из затруднения.
— Расскажите, как вы пытались решить возникшую проблему?
— Какую гипотезу вы можете выдвинуть? (Учащиеся предлагают варианты: обратимая функция должна принимать свое значение только в одной точке)
Попробуем разобраться. Мы все знаем, что полиция часто ловит преступников по отпечаткам пальцев. Можно считать, что снимая отпечатки пальцев у людей, полиция находит функцию «отпечатки пальцев человека» — человеку ставятся в соответствие его отпечатки пальцев. Обнаружив на месте преступления чьи-то отпечатки пальцев, полицейские обращаются к каталогу, находят человека, которому принадлежат эти отпечатки, и вот он, подозреваемый! Можно сказать, что полиция использует обратную функцию к той, что построила, снимая отпечатки пальцев. Представим себе другую ситуацию. Совершено преступление. К счастью, у этого преступления есть свидетели, которые видели преступника. Опрос свидетелей приводит к выводу, что у преступника было две руки. Поможет ли эта информация установить, кто совершил преступление? Вряд ли. В чём разница с ситуацией с отпечатками пальцев? Отпечатки пальцев вещь уникальная, у разных людей разные отпечатки. Какую функцию мы попытались использовать в ситуации со свидетелями? Функцию «количество рук у человека», которая ставит в соответствие человеку количество имеющихся у него рук. По значению этой функции невозможно определить, что за аргумент у неё был, по улицам ходит очень много людей с двумя руками! Итак, для того, чтобы обратная функция существовала, нужно, чтобы каждое значение принималось только один раз. Зная отпечатки пальцев преступника, его поймать можно, зная только количество рук – нет.
На интерактивной доске учитель проводит сравнение графиков двух функций, у которых области определения и множества значений одинаковы, но одна из функций монотонна, а другая нет (рис.2). Таким образом, функция обладает свойством, не характерным для функции : какое бы число из множества значения функции f(x) ни взять, оно является значением функции только в одной точке , тем самым учитель подводит учащихся к понятию обратимой функции.
Рис. 2
Учитель предлагает учащимся сформулировать определение обратимой функции и проводит доказательство теоремы об обратимой функции, используя график монотонной функции на интерактивной доске.
Определение 1. Функцию называют обратимой, если любое свое значение она принимает только в одной точке множества X.
Теорема. Если функция монотонна на множестве X, то она обратима.
Доказательство:
Пусть функция y=f(x) возрастает на множестве Х и пусть х1≠х2 – две точки множества Х.
Для определенности пусть х1< х2. Тогда из того, что х1 < х2 в силу возрастания функции следует, что f(х1) < f(х2).
Таким образом, разным значениям аргумента соответствуют разные значения функции, т.е. функция обратима.
Аналогично доказывается теорема в случае убывающей функции.
(По ходу доказательства теоремы учитель маркером делает все необходимые пояснения на чертеже)
Определение 2. Пусть обратимая функция y=f(x) определена на множестве Х и область ее значений Е(f)=Y. Поставим в соответствие каждому y из Y то единственное значение х, при котором f(x)=y. Тогда получим функцию, которая определена на Y, а Х – область значений функции. Эту функцию обозначают x=f -1(y), и называют обратной по отношению к функции y=f(x),.
6. Реализация построенного проекта.
Обсуждение и сравнение (см. презентацию, слайд № 9). Посмотрим на знакомые нам функции, чтобы понять, какая из предложенных функций обратима, те. у каких из этих функций есть обратные, и как эти обратные функции устроены.
а) б)
Рис. 3 Рис. 4
в) y = 2x + 5; г) y = -х2 + 7.
Замечание. Монотонность функции, является достаточным условием существования обратной функции. Но оно не является необходимым условием.
Учитель предлагает привести примеры различных ситуаций, когда функция не монотонна, но обратима, когда функция не монотонна и не обратима, когда монотонна и обратима.
Можно предложить задание в парах: составить план нахождения обратной функции
Алгоритм составления обратной функции для функции y=f(x), .
Убедиться, что функция y=f(x) обратима на промежутке Х.
Выразить переменную х через у из уравнения y=f(x), учитывая при этом, что .
В полученном равенстве поменять местами х и у. Вместо х=f -1(y) пишут y=f -1(x).
На конкретных примерах учитель показывает как использовать данный алгоритм.
Пример 1. Показать, что для функции y=2x-5 существует обратная функция, и найти ее аналитическое выражение.
Решение. Линейная функция y=2x-5 определена на R, возрастает на R и область ее значений есть R. Значит, обратная функция существует на R. Чтобы найти ее аналитическое выражение, решим уравнение y=2x-5 относительно х; получим . Переобозначим переменные, получим искомую обратную функцию . Она определена и возрастает на R.
Пример 2. Показать, что для функции y=x2, существует обратная функция, найти ее аналитическое выражение и построить график обратной функции.
Решение. Функция непрерывна, монотонна в своей области определения, следовательно, она обратима. Проанализировав области определения и множества значений функции, делается соответствующий вывод об аналитическом выражении для обратной функции, которая имеет вид . Для этого выразим xчерез y : . Переобозначим — обратная функция. Построим графики функций (рис. 5) и убедимся, что они симметричны относительно прямой y=x.

Рис. 5
Учащимся предлагается сделать вывод о связи между областью определения и множеством значений обратных функций.
Область определения исходной функции равна области значений обратной функции и наоборот, область значений исходной функции равна области определения обратной функции. Графики симметричны относительно прямой у=х.
Замечание: монотонность функции, является достаточным условием существования обратной функции. Но оно не является необходимым условием.
7. Физминутка
8. Первичное закрепление (с проговариванием во внешней речи).
Решаем № 10.1(а); 10.3 – устно проговариваем а), б), в), г), строим на доске (а), проговаривая решение; 10.13 (а) – решение у доски
Остальные комментируются аналогично.
№ 10.2(а); 10.3(г)– работа в парах по два примера с последующей самопроверкой по образцу.
9. Самостоятельная работа с самопроверкой по эталону.
— Можете ли вы теперь с уверенностью сказать, что научились находить обратную функцию?
Учащиеся выполняют самостоятельную работу, проверяют по эталону для самопроверки, определяют место, причину допущенных ошибок, исправляют их.
Раздаются карточки – эталоны каждому ученику.
10. Рефлексия деятельности на уроке.
– Что нового вы узнали на уроке?
– Чем пользовались, чтобы вывести новое правило?
– Ваша оценка своей работы на уроке?
Домашнее задание № 10.1 (б); 10.8 (г); 10.9(г)
Творческое задание: Является ли монотонность функции необходимым условием для обратимости? Приведите примеры немонотонных, но обратимых функций.
