Каким свойством обладает средняя линия трапеции

Средняя линия фигур в планиметрии — отрезок, соединяющий середины двух сторон данной фигуры. Понятие употребляется для следующих фигур: треугольник, четырёхугольник, трапеция.
Средняя линия треугольника[править | править код]
Средняя линия треугольника
Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника[1].
Свойства[править | править код]
- средняя линия треугольника параллельна основанию и равна его половине.
- средняя линия отсекает треугольник, подобный и гомотетичный исходному с коэффициентом 1/2; его площадь равна одной четвёртой площади исходного треугольника.
- три средние линии делят исходный треугольник на четыре равных треугольника. Центральный из этих треугольников называется дополнительным или серединным треугольником.
Признаки[править | править код]
- Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок – средняя линия.
Средняя линия четырёхугольника[править | править код]
Средняя линия четырёхугольника — отрезок, соединяющий середины противолежащих сторон четырёхугольника.
Свойства[править | править код]
Первая линия соединяет 2 противоположные стороны.
Вторая соединяет 2 другие противоположные стороны.
Третья соединяет центры двух диагоналей (не во всех четырёхугольниках диагонали пунктом пересечения делятся пополам).
- Если в выпуклом четырёхугольнике средняя линия образует равные углы с диагоналями четырёхугольника, то диагонали равны.
- Длина средней линии четырёхугольника меньше полусуммы двух других сторон или равна ей, если эти стороны параллельны, и только в этом случае.
- Середины сторон произвольного четырёхугольника — вершины параллелограмма. Его площадь равна половине площади четырёхугольника, а его центр лежит на точке пересечения средних линий. Этот параллелограмм называется параллелограммом Вариньона;
- Последний пункт означает следующее: В выпуклом четырёхугольнике можно провести четыре средние линии второго рода. Средние линии второго рода — четыре отрезка внутри четырёхугольника, проходящие через середины его смежных сторон параллельно диагоналям. Четыре средние линии второго рода выпуклого четырёхугольника разрезают его на четыре треугольника и один центральный четырёхугольник. Этот центральный четырёхугольник является параллелограммом Вариньона.
- Точка пересечения средних линий четырёхугольника является их общей серединой и делит пополам отрезок, соединяющий середины диагоналей. Кроме того, она является центроидом вершин четырёхугольника.
- В произвольном четырёхугольнике вектор средней линии равен полусумме векторов оснований.
Средняя линия трапеции[править | править код]
Средняя линия трапеции — отрезок, соединяющий середины боковых сторон этой трапеции. Отрезок, соединяющий середины оснований трапеции, называют второй средней линией трапеции.
Она рассчитывается по формуле: , где AD и BC — основания трапеции.
Свойства[править | править код]
- средняя линия параллельна основаниям
- средняя линия равна полусумме оснований
- cредняя линия разбивает фигуру на две трапеции, площади которых соотносятся как [1]
См. также[править | править код]
- Теорема Вариньона (геометрия)
Примечания[править | править код]
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 января 2020;
проверки требуют 10 правок.
Трапе́ция (от др.-греч. τραπέζιον — «столик» от τράπεζα — «стол») — выпуклый четырёхугольник, у которого две стороны параллельны. Часто в определение трапеции добавляют условие, что две другие стороны должны быть не параллельны[1]. Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами. Средняя линия — отрезок, соединяющий середины боковых сторон.
Варианты определения[править | править код]
Существует и другое определение трапеции.
Трапеция — это выпуклый четырёхугольник, у которого две стороны параллельны[2][3]. Согласно этому определению, параллелограмм и прямоугольник — частные случаи трапеции. Однако при использовании такого определения большинство признаков и свойств равнобедренной трапеции перестают быть верными (так как параллелограмм становится её частным случаем). Приведённые в разделе Общие свойства формулы верны для обоих определений трапеции.
Связанные определения[править | править код]
Элементы трапеции[править | править код]
Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой
- Параллельные противоположные стороны называются основаниями трапеции.
- Две другие стороны называются боковыми сторонами.
- Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
- Углом при основании трапеции называется ее внутренний угол, образованный основанием с боковой стороной.
Виды трапеций[править | править код]
- Трапеция, у которой боковые стороны равны, называется равнобедренной трапецией (реже равнобокой[4] или равнобочной[5] трапецией).
- Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.
Равнобедренная трапеция
Прямоугольная трапеция
Свойства[править | править код]
Основной источник: [6]
- Средняя линия трапеции параллельна основаниям и равна их полусумме.[7]
- Отрезок, соединяющий середины диагоналей трапеции, равен половине разности оснований и лежит на средней линии.
- Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен среднему гармоническому длин оснований трапеции.
- В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон.
- Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
- Если сумма углов при одном из оснований трапеции равна 90°, то продолжения боковых сторон пересекаются под прямым углом, а отрезок, соединяющий середины оснований, равен полуразности оснований.
- Диагонали трапеции делят ее на 4 треугольника. Два из них, прилежащие к основаниям, подобны. Два других, прилежащие к боковым сторонам, имеют одинаковую площадь.
- Если отношение оснований равно , то отношение площадей треугольников, прилежащих к основаниям, равно .
- Высота трапеции определяется формулой:
где — большее основание, — меньшее основание, и — боковые стороны.
Их можно выразить в явном виде:
Если, наоборот, известны боковые стороны и диагонали, то основания выражаются формулами:
а при известных основаниях и диагоналях боковые стороны следующие:
Если же известна высота , то
- Прямая Гаусса для трапеции совпадает с ее средней линией.
Равнобедренная трапеция[править | править код]
Трапеция является равнобедренной тогда и только тогда, когда выполнено любое из следующих эквивалентных условий:
- прямая, которая проходит через середины оснований, перпендикулярна основаниям (то есть является осью симметрии трапеции);
- высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований;
- углы при любом основании равны;
- сумма противоположных углов равна 180°;
- длины диагоналей равны;
- вокруг этой трапеции можно описать окружность;
- вершинами этой трапеции также являются вершины некоторого антипараллелограмма.
Кроме того
- если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная и описанная окружность[править | править код]
- Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований).
- В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
- Если трапецию можно вписать в окружность — то она равнобедренная.
- Радиус описанной окружности равнобедренной трапеции:[источник не указан 1810 дней]
где — боковая сторона, — бо́льшее основание, — меньшее основание, — диагонали равнобедренной трапеции.
- Если , то в равнобедренную трапецию можно вписать окружность радиуса
Площадь[править | править код]
Здесь приведены формулы, свойственные именно трапеции. См. также формулы для площади произвольных четырёхугольников.
Примечание: Приведённые выше две формулы эквивалентны, так как полусумма оснований равняется средней линии трапеции:
или
- Средняя линия разбивает фигуру на две трапеции, площади которых соотносятся как[8]
- Площадь равнобедренной трапеции:
где — боковая сторона, — бо́льшее основание, — меньшее основание, — угол между бо́льшим основанием и боковой стороной[9].
- Площадь равнобедренной трапеции через её стороны
История[править | править код]
Слово «трапеция» происходит от греческого слова др.-греч. τραπέζιον «столик» (уменьш. от τράπεζα «стол»), означающего стол. В русском языке от этого слова происходит слово «трапеза» (еда).
Примечания[править | править код]
[{Large{text{Произвольная трапеция}}}]
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.
Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.
Теоремы: свойства трапеции
1) Сумма углов при боковой стороне равна (180^circ).
2) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.
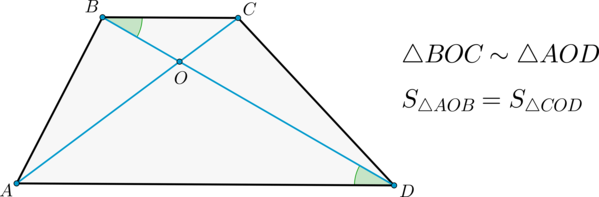
Доказательство
1) Т.к. (ADparallel BC), то углы (angle BAD) и (angle ABC) – односторонние при этих прямых и секущей (AB), следовательно, (angle
BAD
+angle ABC=180^circ).
2) Т.к. (ADparallel BC) и (BD) – секущая, то (angle DBC=angle
BDA) как накрест лежащие.
Также (angle BOC=angle AOD) как вертикальные.
Следовательно, по двум углам (triangle BOC sim triangle AOD).
Докажем, что (S_{triangle AOB}=S_{triangle COD}). Пусть (h) – высота трапеции. Тогда (S_{triangle ABD}=frac12cdot hcdot
AD=S_{triangle ACD}). Тогда: [S_{triangle AOB}=S_{triangle ABD}-S_{triangle AOD}=S_{triangle ACD}-S_{triangle AOD}=S_{triangle
COD}]
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
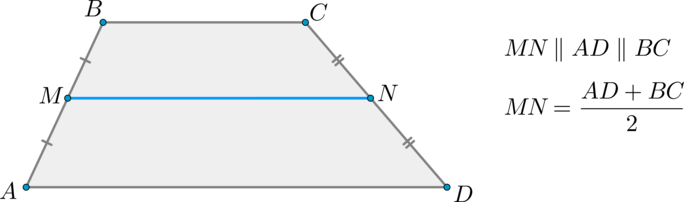
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем параллельность.
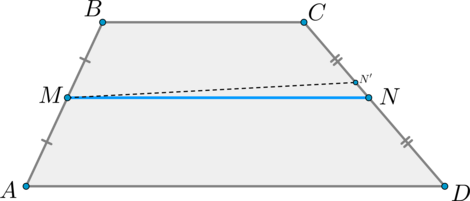
Проведем через точку (M) прямую (MN’parallel AD) ((N’in CD)). Тогда по теореме Фалеса (т.к. (MN’parallel ADparallel BC, AM=MB)) точка (N’) — середина отрезка (CD). Значит, точки (N) и (N’) совпадут.
2) Докажем формулу.
Проведем (BB’perp AD, CC’perp AD). Пусть (BB’cap MN=M’, CC’cap
MN=N’).
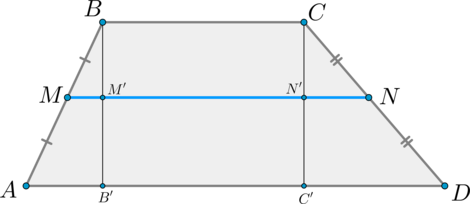
Тогда по теореме Фалеса (M’) и (N’) — середины отрезков (BB’) и (CC’) соответственно. Значит, (MM’) – средняя линия (triangle
ABB’), (NN’) — средняя линия (triangle DCC’). Поэтому: [MM’=dfrac12 AB’, quad NN’=dfrac12 DC’]
Т.к. (MNparallel ADparallel BC) и (BB’, CC’perp AD), то (B’M’N’C’) и (BM’N’C) – прямоугольники. По теореме Фалеса из (MNparallel AD) и (AM=MB) следует, что (B’M’=M’B). Значит, (B’M’N’C’) и (BM’N’C) – равные прямоугольники, следовательно, (M’N’=B’C’=BC).
Таким образом:
[MN=MM’+M’N’+N’N=dfrac12 AB’+B’C’+dfrac12 C’D=] [=dfrac12 left(AB’+B’C’+BC+C’Dright)=dfrac12left(AD+BCright)]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
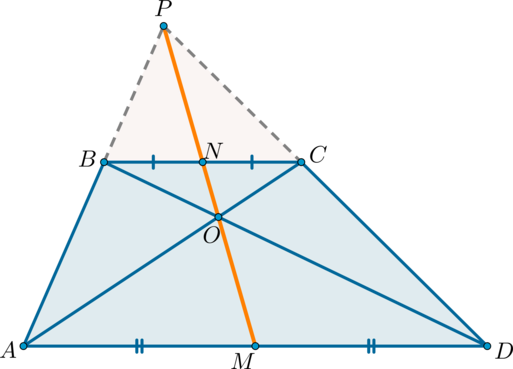
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки (P), (N) и (M) лежат на одной прямой.
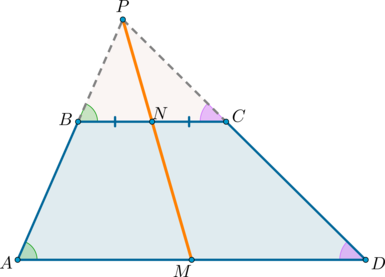
Проведем прямую (PN) ((P) – точка пересечения продолжений боковых сторон, (N) – середина (BC)). Пусть она пересечет сторону (AD) в точке (M). Докажем, что (M) – середина (AD).
Рассмотрим (triangle BPN) и (triangle APM). Они подобны по двум углам ((angle APM) – общий, (angle PAM=angle PBN) как соответственные при (ADparallel BC) и (AB) секущей). Значит: [dfrac{BN}{AM}=dfrac{PN}{PM}]
Рассмотрим (triangle CPN) и (triangle DPM). Они подобны по двум углам ((angle DPM) – общий, (angle PDM=angle PCN) как соответственные при (ADparallel BC) и (CD) секущей). Значит: [dfrac{CN}{DM}=dfrac{PN}{PM}]
Отсюда (dfrac{BN}{AM}=dfrac{CN}{DM}). Но (BN=NC), следовательно, (AM=DM).
2) Докажем, что точки (N, O, M) лежат на одной прямой.
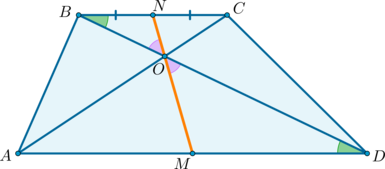
Пусть (N) – середина (BC), (O) – точка пересечения диагоналей. Проведем прямую (NO), она пересечет сторону (AD) в точке (M). Докажем, что (M) – середина (AD).
(triangle BNOsim triangle DMO) по двум углам ((angle OBN=angle
ODM) как накрест лежащие при (BCparallel AD) и (BD) секущей; (angle BON=angle DOM) как вертикальные). Значит: [dfrac{BN}{MD}=dfrac{ON}{OM}]
Аналогично (triangle CONsim triangle AOM). Значит: [dfrac{CN}{MA}=dfrac{ON}{OM}]
Отсюда (dfrac{BN}{MD}=dfrac{CN}{MA}). Но (BN=CN), следовательно, (AM=MD).
[{Large{text{Равнобедренная трапеция}}}]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию (ABCD).
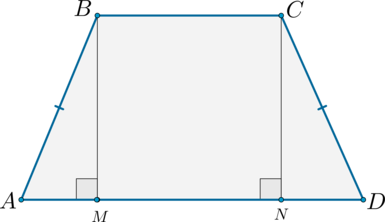
Из вершин (B) и (C) опустим на сторону (AD) перпендикуляры (BM) и (CN) соответственно. Так как (BMperp AD) и (CNperp AD), то (BMparallel CN); (ADparallel BC), тогда (MBCN) – параллелограмм, следовательно, (BM = CN).
Рассмотрим прямоугольные треугольники (ABM) и (CDN). Так как у них равны гипотенузы и катет (BM) равен катету (CN), то эти треугольники равны, следовательно, (angle DAB = angle CDA).
2) 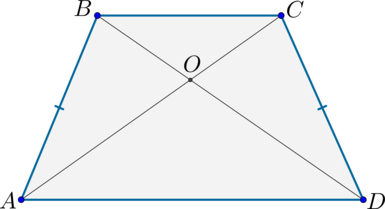
Т.к. (AB=CD, angle A=angle D, AD) – общая, то по первому признаку (triangle ABD=triangle ACD). Следовательно, (AC=BD).
3) Т.к. (triangle ABD=triangle ACD), то (angle BDA=angle CAD). Следовательно, треугольник (triangle AOD) – равнобедренный. Аналогично доказывается, что и (triangle BOC) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Рассмотрим трапецию (ABCD), такую что (angle A = angle D).
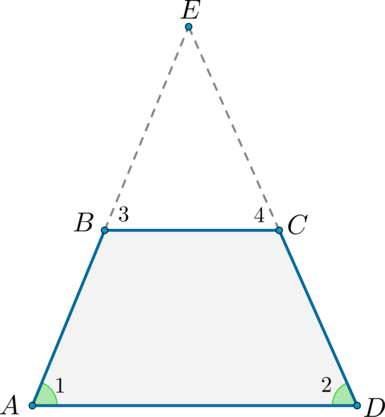
Достроим трапецию до треугольника (AED) как показано на рисунке. Так как (angle 1 = angle 2), то треугольник (AED) равнобедренный и (AE
= ED). Углы (1) и (3) равны как соответственные при параллельных прямых (AD) и (BC) и секущей (AB). Аналогично равны углы (2) и (4), но (angle 1 = angle 2), тогда (angle 3 = angle 1 = angle 2 =
angle 4), следовательно, треугольник (BEC) тоже равнобедренный и (BE = EC).
В итоге (AB = AE — BE = DE — CE = CD), то есть (AB = CD), что и требовалось доказать.
2) Пусть (AC=BD). Т.к. (triangle AODsim triangle BOC), то обозначим их коэффициент подобия за (k). Тогда если (BO=x), то (OD=kx). Аналогично (CO=y Rightarrow AO=ky).
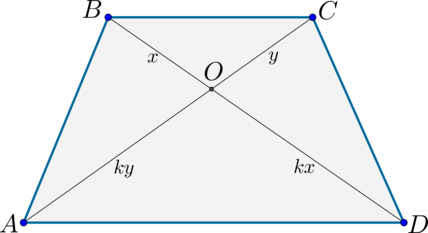
Т.к. (AC=BD), то (x+kx=y+ky Rightarrow x=y). Значит (triangle AOD) – равнобедренный и (angle OAD=angle ODA).
Таким образом, по первому признаку (triangle ABD=triangle ACD) ((AC=BD, angle OAD=angle ODA, AD) – общая). Значит, (AB=CD), чтд.
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Что такое трапеция?
СОДЕРЖАНИЕ СТАТЬИ
 | Трапеция – такой четырехугольник, у которого две стороны параллельны, а две другие – нет. |
Параллельные стороны называются – основания, а непараллельные стороны называются боковые стороны.
Вот, смотри:

Оказывается, трапеция (как и треугольник) бывает равнобедренная.
 | Если боковые стороны равны, то она называется равнобедренной, или равнобокой. |
И тут возникает вопрос: а могут ли у трапеции быть равными ОСНОВАНИЯ??? И ответ: а вот и нет — тогда это получится НЕ трапеция, а параллелограмм, потому что две стороны окажутся параллельны и равны (вспоминаем признаки параллелограмма…)
Свойства трапеции
Свойства трапеции… Какие они и что же ты должен знать о них?
 | Сумма углов при каждой боковой стороне трапеции равна 180°. (у нас на рисунке и ) |
Почему так? Ну, конечно, просто потому, что основания – параллельны, а боковая сторона – секущая. Вот и получается, что и – внутренние односторонние углы при параллельных и и секущей . Поэтому . И точно так же и – внутренние односторонние углы при тех же параллельных и , но секущая теперь – .
Видишь: главное, что играет роль – это параллельность оснований. Давай разберем еще некоторые свойства трапеции.
Как у всякого четырехугольника, у трапеции есть диагонали. Их две – посмотри на рисунки:
Ну вот, а теперь снова порассуждаем об углах.
 | Опять и – параллельные, а диагональ – секущая. Поэтому . |
А теперь – сразу 2 диагонали и 4 угла:
 | |
Что из этого может следовать? Очень важный факт: треугольники и – подобны по двум углам.
Их коэффициент подобия равен отношению оснований: .
Средняя линия трапеции
Для начала – что же такое средняя линия трапеции?
 | Средняя линия трапеции – это отрезок, который соединяет середины боковых сторон трапеции. |
Оказывается, длину этой средней линии можно выразить через длины оснований трапеции. А именно, имеет место такая формула:
 | , то есть |
Длина средней линии трапеции равна полусумме (то есть половине суммы) длин оснований
А ещё:
Средняя линия трапеции параллельна ее основаниям
Трапеция, вписанная в окружность.
Даже если ты ещё не изучал темы «Окружность. Вписанный угол» и «Вписанный четырехугольник», тебе будет полезно (и, надеюсь, интересно) узнать следующий удивительный факт:
 | Если трапецию можно вписать в окружность, то она – равнобокая. |
Доказывать это мы не будем (здесь во всяком случае), а вот запомнить – хорошо бы – пригодится!
Подведём итог – он короткий.
Самое важное, что есть в трапеции – две параллельные стороны и BCE свойства трапеции именно этим и определяются.
Так что, если у тебя в задаче трапеция – используй параллельность – всё получится!
ТРАПЕЦИЯ. СРЕДНИЙ УРОВЕНЬ
Трапеция. Основные понятия и определения
Трапеция – четырёхугольник, у которого две стороны параллельны, а две другие – нет.

Параллельные стороны называются основаниями, а непараллельные – боковыми сторонами.
 | Если боковые стороны трапеции равны, то она называется равнобедренной или равнобокой. |
Свойства трапеции
Свойства трапеции… Какие они и что же ты должен о них знать? Рассмотрим основные свойства трапеции.
Первое свойство трапеции
 | Сумма угловпри каждой боковой стороне трапеции равна . |
Почему? и – параллельны, а и – секущие, поэтому:
Второе свойство трапеции
 | Треугольники и подобны по двум углам. ( и – как накрест лежащие) |
Коэффициент подобия треугольников и равен отношению оснований:
Третье свойство трапеции
Сначала сформулируем основное определение, которое тебе нужно знать для понимания этого свойства трапеции:
 | Средняя линия трапеции – отрезок, соединяющий середины боковых сторон. |
А теперь формула:
А вот и само третье свойство трапеции:
Средняя линия трапеции равна полусумме оснований и параллельна им.
А это почему? Ту чуть – чуть сложнее – потребуется провести аж одну лишнюю линию!

Итак, проведём . Тогда четырехугольник – параллелограмм. Возьмём середину стороны и середину стороны . Оба: и – снова параллелограммы ( и ; и ). Ну вот, значит , да ещё .
Поедем дальше.
 | Проведём — среднюю линию в . Знаем, что и |
Что же из всего этого следует?
 |
|
Вот и доказали!
Четвертое свойство трапеции
 | Если трапеция вписана в окружность, то она равнобокая. |
Почему? Подробнее смотри в теме «Вписанный четырехугольник», а тут – двумя строчками:
(трапеция же!)
(вписанный четырехугольник)
. Ну, и так же .
Пятое свойство трапеции
 | В ЛЮБОЙ трапеции следующие четыре точки лежат на одной прямой: 1) – точка пересечения продолжений боковых сторон; 2) и – середины оснований; 3) – точка пересечения диагоналей. |
Эту теорему доказывать не будем – не пугайся.
Заметим только, что ВЕРНО и ОБРАТНОЕ:
Если в каком – нибудь четырехугольнике какие – нибудь три из перечисленных четырёх точек окажутся на одной прямой – то четырёхугольник этот – ТРАПЕЦИЯ.
Шестое свойство трапеции
 | Биссектрисы углов при боковой стороне трапеции перпендикулярны. |
Седьмое свойство трапеции
Здесь мы ещё раз увидим, как полезно в трапеции бывает провести линию, параллельную или боковой стороне, или диагонали – сразу появляется новый взгляд. Один раз мы уже так делали – в пункте про среднюю линию. А теперь ты узнал новый факт, который относительно часто встречается в задачах.
 | В трапеции с перпендикулярными диагоналями |
Давай докажем! Это уже целая задача, которая вполне может попасться прямо на экзамене!
Ну вот, и ты теперь старайся с помощью новых знаний и методов решать задачки про трапецию – они обычно не слишком сложные. Главное, твёрдо помнить все свойства трапеции и не забывать о параллельности оснований и иногда (в задачах посложнее) бывает полезно провести что-то параллельное или соединить боковые стороны.

Проведём и .
Обозначим ; .
Тогда:
- – прямоугольный
Значит, (медиана, проведенная к гипотенузе, равна её половине).
То есть .
Но ведь (так как — параллелограмм) .
ТРАПЕЦИЯ. КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ
Трапеция – четырёхугольник, у которого две стороны параллельны (они называются основания), а две другие – нет (это боковые стороны).
 |
|
 |
|
- Средняя линия параллельна основаниям: .
- Длина средней линии трапеции равна полусумме длин оснований: .
 |
|
- Треугольники, образованные основаниями трапеции и отрезками диагоналей
( и ) подобны по двум углам с коэффициентом подобия равным отношению оснований: . - Площади треугольников, образованных боковыми сторонами и отрезками диагоналей трапеции, равны: .
 |
|
Свойства равнобедренной трапеции:
- диагонали равны: ;
- углы при основании равны: ;
- сумма противолежащих углов равна : .
 |
|
Стороны и диагональ равнобокой трапеции связаны соотношением: .
Площадь трапеции равна полусумме оснований, умноженной на высоту: .
ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!
Стать учеником YouClever,
Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц»,
А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.
