Каким свойством обладает катушка

Приветствую всех на нашем сайте!
Мы продолжаем изучать электронику с самых основ, и темой сегодняшней статьи будет катушка индуктивности. Забегая вперед скажу, что сначала мы обсудим теоретические аспекты, а несколько будущих статей посвятим целиком и полностью рассмотрению различных электрических схем, в которых используются катушки индуктивности, а также элементы, которые мы изучили ранее в рамках нашего курса – резисторы и конденсаторы.
Устройство и принцип работы катушки индуктивности.
Как уже понятно из названия элемента – катушка индуктивности, в первую очередь, представляет из себя именно катушку ???? То есть большое количество витков изолированного проводника. Причем наличие изоляции является важнейшим условием – витки катушки не должны замыкаться друг с другом. Чаще всего витки наматываются на цилиндрический или тороидальный каркас:

Важнейшей характеристикой катушки индуктивности является, естественно, индуктивность, иначе зачем бы ей дали такое название ???? Индуктивность – это способность преобразовывать энергию электрического поля в энергию магнитного поля. Это свойство катушки связано с тем, что при протекании по проводнику тока вокруг него возникает магнитное поле:
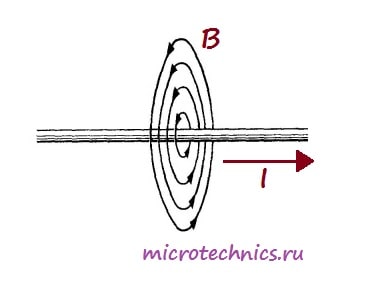
А вот как выглядит магнитное поле, возникающее при прохождении тока через катушку:
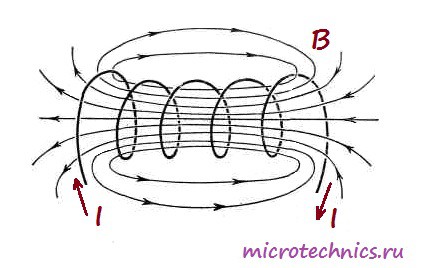
В общем то, строго говоря, любой элемент в электрической цепи имеет индуктивность, даже обычный кусок провода. Но дело в том, что величина такой индуктивности является очень незначительной, в отличие от индуктивности катушек. Собственно, для того, чтобы охарактеризовать эту величину используется единица измерения Генри (Гн). 1 Генри – это на самом деле очень большая величина, поэтому чаще всего используются мкГн (микрогенри) и мГн (милигенри). Величину индуктивности катушки можно рассчитать по следующей формуле:
L = frac{mu_0thinspace mu S N^2}{l}
Давайте разберемся, что за величину входят в это выражение:
- mu_0 – магнитная проницаемость вакуума. Это табличная величина (константа) и равна она следующему значению: mu_0 = 4 pi cdot 10^{-7}medspacefrac{Гн}{м}
- mu – магнитная проницаемость магнитного материала сердечника. А что это за сердечник и для чего он нужен? Сейчас выясним. Дело все в том, что если катушку намотать не просто на каркас (внутри которого воздух), а на магнитный сердечник, то индуктивность возрастет многократно. Посудите сами – магнитная проницаемость воздуха равна 1, а для никеля она может достигать величины 1100. Вот мы и получаем увеличение индуктивности более чем в 1000 раз
- S – площадь поперечного сечения катушки
- N – количество витков
- l – длина катушки
Из формулы следует, что при увеличении числа витков или, к примеру, диаметра (а соответственно и площади поперечного сечения) катушки, индуктивность будет увеличиваться. А при увеличении длины – уменьшаться. Таким образом, витки на катушке стоит располагать как можно ближе друг к другу, поскольку это приведет к уменьшению длины катушки.
С устройством катушки индуктивности мы разобрались, пришло время рассмотреть физические процессы, которые протекают в этом элементе при прохождении электрического тока. Для этого мы рассмотрим две схемы – в одной будем пропускать через катушку постоянный ток, а в другой -переменный!
Катушка индуктивности в цепи постоянного тока.
Итак, в первую очередь, давайте разберемся, что же происходит в самой катушке при протекании тока. Если ток не изменяет своей величины, то катушка не оказывает на него никакого влияния. Значит ли это, что в случае постоянного тока использование катушек индуктивности и рассматривать не стоит? А вот и нет ???? Ведь постоянный ток можно включать/выключать, и как раз в моменты переключения и происходит все самое интересное. Давайте рассмотрим цепь:

Резистор выполняет в данном случае роль нагрузки, на его месте могла бы быть, к примеру, лампа. Помимо резистора и индуктивности в цепь включены источник постоянного тока и переключатель, с помощью которого мы будем замыкать и размыкать цепь. Что же произойдет в тот момент когда мы замкнем выключатель?
Ток через катушку начнет изменяться, поскольку в предыдущий момент времени он был равен 0. Изменение тока приведет к изменению магнитного потока внутри катушки, что, в свою очередь, вызовет возникновение ЭДС (электродвижущей силы) самоиндукции, которую можно выразить следующим образом:
varepsilon_s = -frac{dPhi}{dt}
Возникновение ЭДС приведет к появлению индукционного тока в катушке, который будет протекать в направлении, противоположном направлению тока источника питания. Таким образом, ЭДС самоиндукции будет препятствовать протеканию тока через катушку (индукционный ток будет компенсировать ток цепи из-за того, что их направления противоположны). А это значит, что в начальный момент времени (непосредственно после замыкания выключателя) ток через катушку I_L будет равен 0. В этот момент времени ЭДС самоиндукции максимальна. А что же произойдет дальше? Поскольку величина ЭДС прямо пропорциональна скорости изменения тока, то она будет постепенно ослабевать, а ток, соответственно, наоборот будет возрастать. Давайте посмотрим на графики, иллюстрирующие то, что мы обсудили:
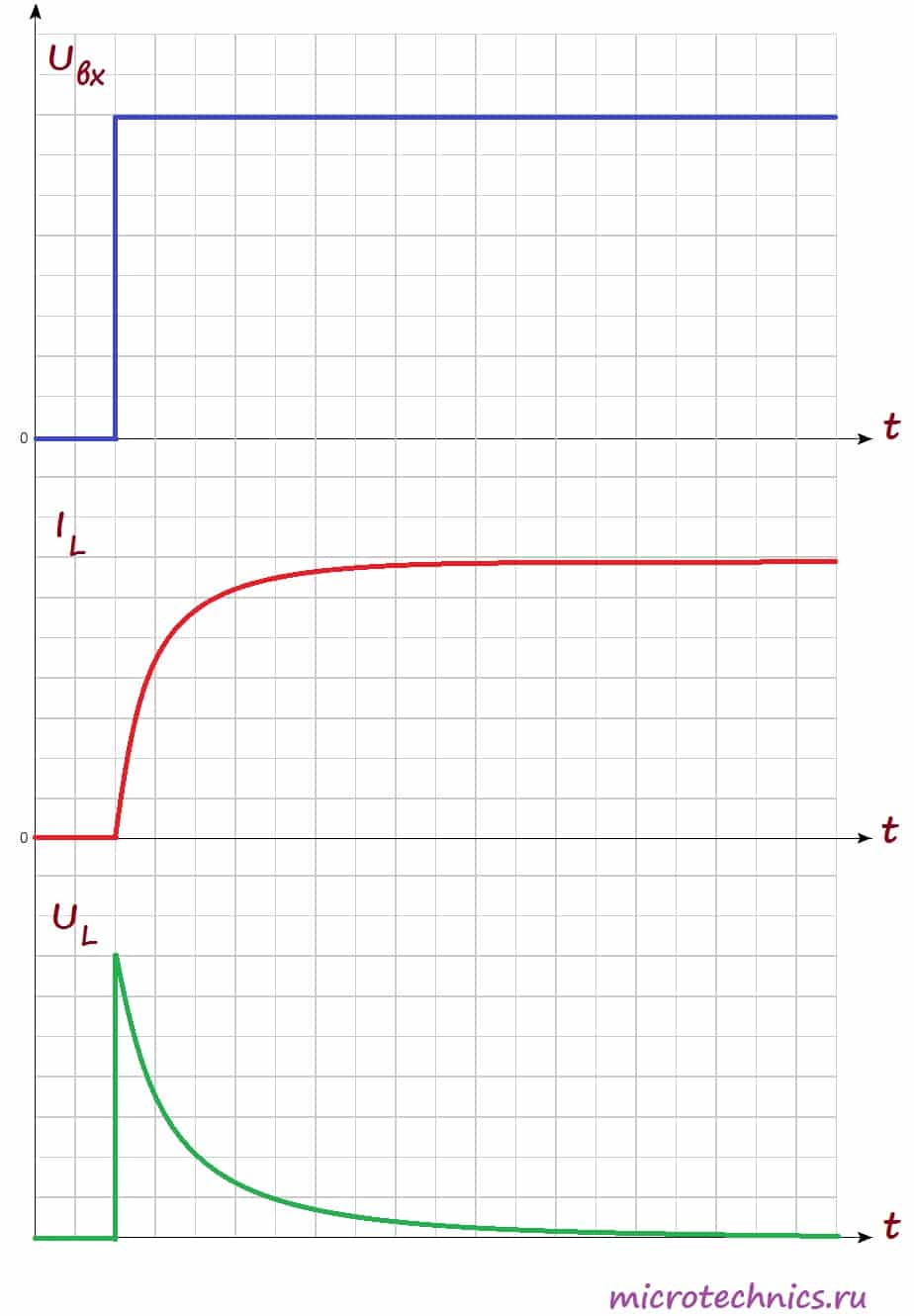
На первом графике мы видим входное напряжение цепи – изначально цепь разомкнута, а при замыкании переключателя появляется постоянное значение. На втором графике мы видим изменение величины тока через катушку индуктивности. Непосредственно после замыкания ключа ток отсутствует из-за возникновения ЭДС самоиндукции, а затем начинает плавно возрастать.
Напряжение на катушке наоборот в начальный момент времени максимально, а затем уменьшается. График напряжения на нагрузке будет по форме (но не по величине) совпадать с графиком тока через катушку (поскольку при последовательном соединении ток, протекающий через разные элементы цепи одинаковый). Таким образом, если в качестве нагрузки мы будем использовать лампу, то они загорится не сразу после замыкания переключателя, а с небольшой задержкой (в соответствии с графиком тока).
Аналогичный переходный процесс в цепи будет наблюдаться и при размыкании ключа. В катушке индуктивности возникнет ЭДС самоиндукции, но индукционный ток в случае размыкания будет направлен в том же самом направлении, что и ток в цепи, а не в противоположном, поэтому запасенная энергия катушки индуктивности пойдет на поддержание тока в цепи:
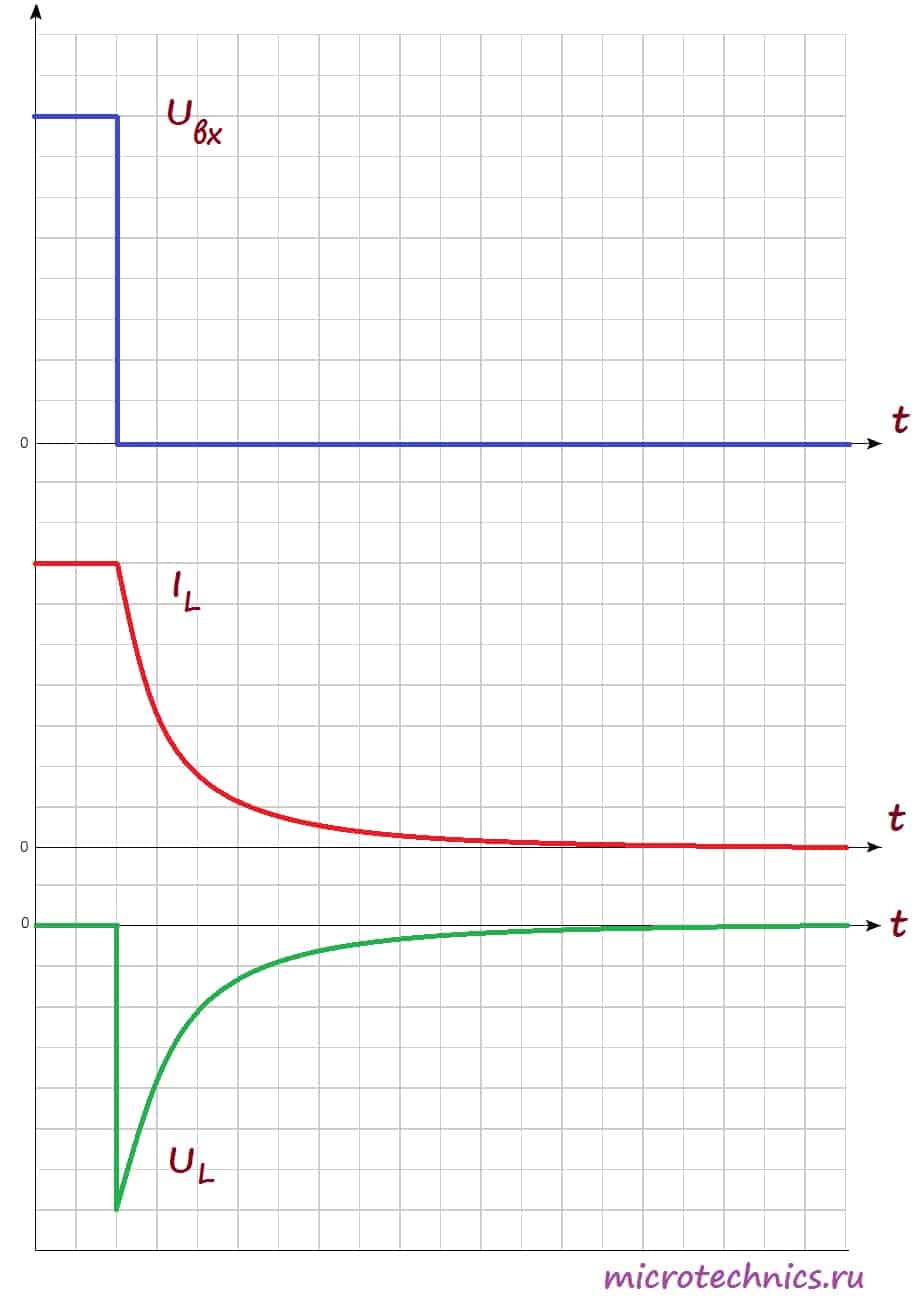
После размыкания ключа возникает ЭДС самоиндукции, которая препятствует уменьшению тока через катушку, поэтому ток достигает нулевого значения не сразу, а по истечении некоторого времени. Напряжение же в катушке по форме идентично случаю замыкания переключателя, но противоположно по знаку. Это связано с тем, что изменение тока, а соответственно и ЭДС самоиндукции в первом и втором случаях противоположны по знаку (в первом случае ток возрастает, а во втором убывает).
Кстати, я упомянул, что величина ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, так вот, коэффициентом пропорциональности является ни что иное как индуктивность катушки:
varepsilon_s = -Lmedspacefrac{dI}{dt}
На этом мы заканчиваем с катушками индуктивности в цепях постоянного тока и переходим к цепям переменного тока.
Катушка индуктивности в цепи переменного тока.
Рассмотрим цепь, в которой на катушку индуктивности подается переменный ток:
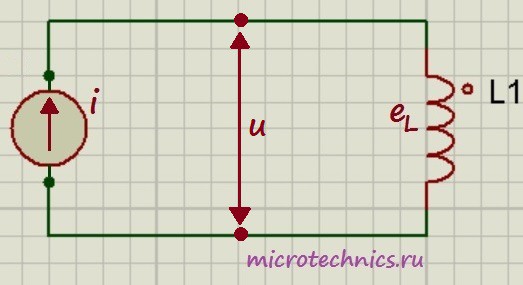
Давайте посмотрим на зависимости тока и ЭДС самоиндукции от времени, а затем уже разберемся, почему они выглядят именно так:
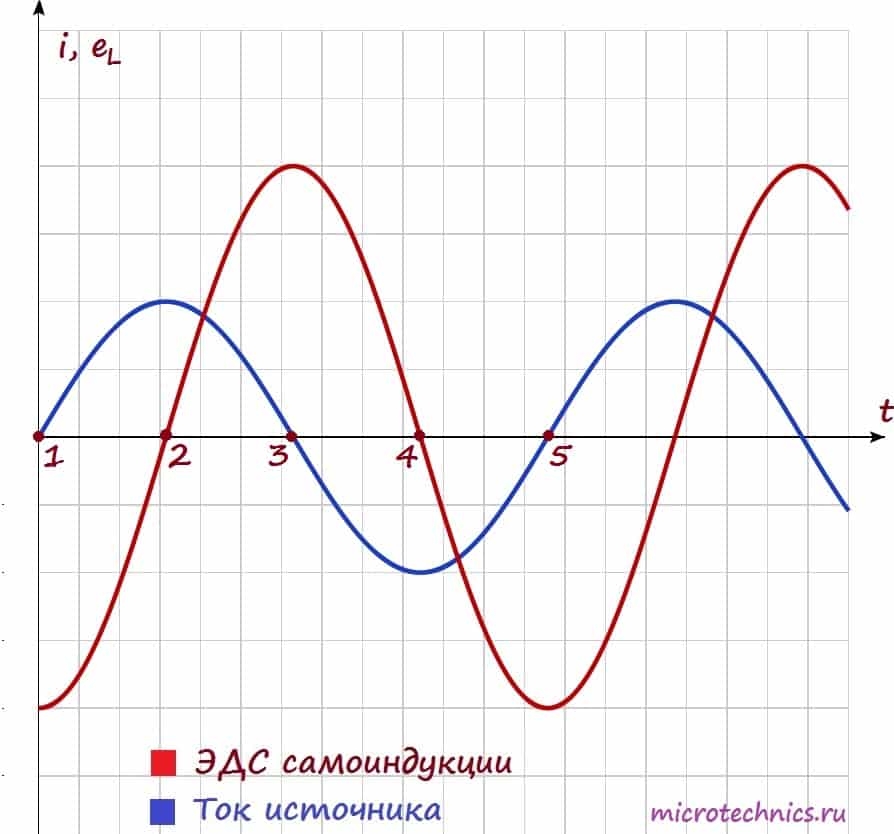
Как мы уже выяснили ЭДС самоиндукции у нас прямо пропорциональна и противоположна по знаку скорости изменения тока:
varepsilon_L = -Lmedspacefrac{dI}{dt}
Собственно, график нам и демонстрирует эту зависимость! Смотрите сами – между точками 1 и 2 ток у нас изменяется, причем чем ближе к точке 2, тем изменения меньше, а в точке 2 в течении какого-то небольшого промежутка времени ток и вовсе не изменяет своего значения. Соответственно скорость изменения тока максимальна в точке 1 и плавно уменьшается при приближении к точке 2, а в точке 2 равна 0, что мы и видим на графике ЭДС самоиндукции. Причем на всем промежутке 1-2 ток возрастает, а значит скорость его изменения положительна, в связи с этим на ЭДС на всем этом промежутке напротив принимает отрицательные значения.
Аналогично между точками 2 и 3 – ток уменьшается – скорость изменения тока отрицательная и увеличивается – ЭДС самоиндукции увеличивается и положительна. Не буду расписывать остальные участки графика – там все процессы протекают по такому же принципу ????
Кроме того, на графике можно заметить очень важный момент – при увеличении тока (участки 1-2 и 3-4) ЭДС самоиндукции и ток имеют разные знаки (участок 1-2: varepsilon < 0, i > 0, участок 3-4: varepsilon > 0, i < 0). Таким образом, ЭДС самоиндукции препятствует возрастанию тока (индукционные токи направлены “навстречу” току источника).
А на участках 2-3 и 4-5 все наоборот – ток убывает, а ЭДС препятствует убыванию тока (поскольку индукционные токи будут направлены в ту же сторону, что и ток источника и будут частично компенсировать уменьшение тока).
И в итоге мы приходим к очень интересному факту – катушка индуктивности оказывает сопротивление переменному току, протекающему по цепи. А значит она имеет сопротивление, которое называется индуктивным или реактивным и вычисляется следующим образом:
X_L = wmedspace L
Где w – круговая частота: w = 2 pi f. [/latex]f[/latex] – это частота переменного тока. Таким образом, чем больше частота тока, тем большее сопротивление будет ему оказывать катушка индуктивности. А если ток постоянный (f = 0), то реактивное сопротивление катушки равно 0, соответственно, она не оказывает влияния на протекающий ток.
Давайте вернемся к нашим графикам, которые мы построили для случая использования катушки индуктивности в цепи переменного тока. Мы определили ЭДС самоиндукции катушки, но каким же будет напряжение u? Здесь все на самом деле просто! По 2-му закону Кирхгофа:
u + varepsilon_L = 0
А следовательно:
u = – varepsilon_L
Построим на одном графике зависимости тока и напряжения в цепи от времени:
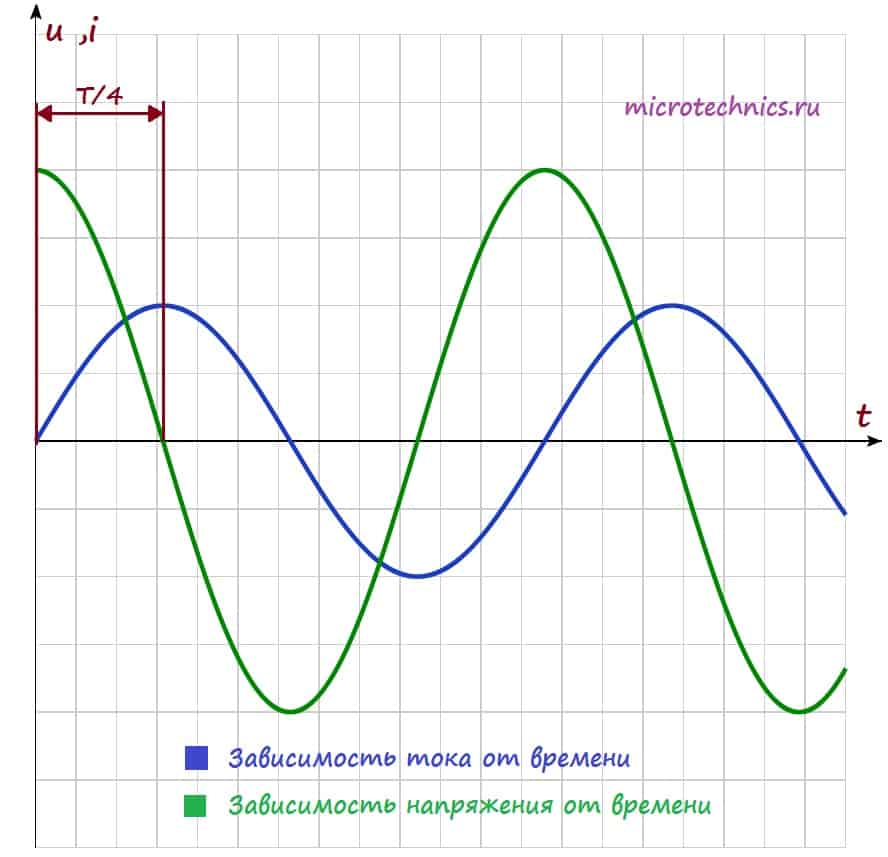
Как видите ток и напряжение сдвинуты по фазе (ссылка) друг относительно друга, и это является одним из важнейших свойств цепей переменного тока, в которых используется катушка индуктивности:
При включении катушки индуктивности в цепь переменного тока в цепи появляется сдвиг фаз между напряжением и током, при этом ток отстает по фазе от напряжения на четверть периода.
Вот и с включением катушки в цепь переменного тока мы разобрались!
На этом, пожалуй, закончим сегодняшнюю статью, она получилась уже довольно объемной, поэтому разговор о катушках индуктивности мы продолжим в следующий раз. Так что до скорых встреч, будем рады видеть вас на нашем сайте!
Ñëîâîñî÷åòàíèå «êàòóøêà íèòîê» çíàêîìî âñåì, íî ïðî êàòóøêó èíäóêòèâíîñòè ñëûøàëè, äóìàþ, íå âñå. Âîò ÷òî âû ñåáå ïðåäñòàâëÿåòå ïîä ñëîâîì «êàòóøêà» ? Íó… ýòî, íàâåðíîå, êàêàÿ-íèáóäü ôèãîâèíêà, íà êîòîðîé íàìîòàíû íèòêè, ëåñêà, âåðåâêà, äà ÷òî óãîäíî! Êàòóøêà èíäóêòèâíîñòè ïðåäñòàâëÿåò èç ñåáÿ òî÷ü-â-òî÷ü òî æå ñàìîå, íî âìåñòî íèòêè, ëåñêè èëè ÷åãî-íèáóäü åùå òàì íàìîòàíà îáûêíîâåííàÿ ìåäíàÿ ïðîâîëîêà â èçîëÿöèè. Èçîëÿöèÿ ìîæåò áûòü èç áåñöâåòíîãî ëàêà, èç ïðîâîäíîé èçîëÿöèè, è äàæå èç ìàòåð÷àòîé. Òóò ôèøêà òàêàÿ, õîòü è ïðîâîäà â êàòóøêå èíäóêòèâíîñòè î÷åíü ïëîòíî ïðèëåãàþò ê äðóã äðóãó, îíè âñå ðàâíî èçîëèðîâàíû äðóã îò äðóãà. Åñëè áóäåòå ìîòàòü êàòóøêè èíäóêòèâíîñòè ñàìè, íè â êîåì ñëó÷àå íå âçäóìàéòå áðàòü îáû÷íûé ìåäíûé ãîëûé ïðîâîä!
Ëþáàÿ êàòóøêà èíäóêòèâíîñòè, êàê íè ñòðàííî, îáëàäàåò èíäóêòèâíîñòüþ 🙂 Èíäóêòèâíîñòü êàòóøêè èçìåðÿåòñÿ â Ãåíðè (Ãí), îáîçíà÷àåòñÿ áóêîâêîé L è çàìåðÿåòñÿ LC — ìåòðîì. ×òî òàêîå èíäóêòèâíîñòü? Äàâàéòå ðàçáèðàòüñÿ. Åñëè ÷åðåç ïðîâîäîê ïðîãíàòü ýëåêòðè÷åñêèé òîê, òî îí âîêðóã ñåáÿ ñîçäàñò ìàãíèòíîå ïîëå:

ãäå Â — ìàãíèòíîå ïîëå , I — ñèëà òîêà.
À äàâàéòå âîçüìåì è íàìîòàåì â ñïèðàëüêó ýòîò ïðîâîä è ïîäàäèì íà åãî êîíöû ýëåêòðè÷åñêèé òîê:

È ó íàñ ïîëó÷èëàñü âîò òàêàÿ êàðòèíà ñ ìàãíèòíûìè ñèëîâûìè ëèíèÿìè:

Ãðóáî ãîâîðÿ, ÷åì áîëüøå ëèíèé ìàãíèòíîãî ïîëÿ ïåðåñåêóò ïëîùàäü ýòîãî ñîëåíîèäà, ïîëó÷àåòñÿ ïëîùàäü öèëèíäðà, òåì áîëüøå áóäåò ìàãíèòíûé ïîòîê (Ô). Òàê êàê ïî âñåé ýòîé êîíñòðóêöèè òå÷åò ýëåêòðè÷åñêèé òîê, òî çíà÷èò â ýòîò ìîìåíò îí îáëàäàåò êàêîé-òî Ñèëîé òîêà (I). À êîýôôèöèåíò ìåæäó ìàãíèòíûì ïîòîêîì è ñèëîé òîêà íàçûâàåòñÿ èíäóêòèâíîñòüþ, è âû÷èñëÿåòñÿ òàê:
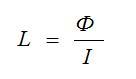
Ñ íàó÷íîé æå òî÷êè çðåíèÿ, èíäóêòèâíîñòü — ýòî ñïîñîáíîñòü èçâëåêàòü ýíåðãèþ èç èñòî÷íèêà ýëåêòðè÷åñêîãî òîêà è ñîõðàíÿòü åå â âèäå ìàãíèòíîãî ïîëÿ. Åñëè òîê â êàòóøêå óâåëè÷èâàåòñÿ, ìàãíèòíîå ïîëå âîêðóã êàòóøêè ðàñøèðÿåòñÿ, à åñëè òîê óìåíüøàåòñÿ — ìàãíèòíîå ïîëå ñæèìàåòñÿ. Êàòóøêà èíäóêòèâíîñòè îáëàäàåò òàêæå î÷åíü èíòåðåñíûìè ñâîéñòâàìè. Ïðè ïîäà÷å íà êàòóøêó ýëåêòðè÷åñêîãî òîêà ïîñòîÿííîãî íàïðÿæåíèÿ, â êàòóøêå âîçíèêàåò íàïðÿæåíèå, ïðîòèâîïîëîæíîå íàïðÿæåíèþ ýëåêòðè÷åñêîãî òîêà è îíî ïîòîì èñ÷åçàåò ÷åðåç íåñêîëüêî äîëåé ñåêóíä. Ýòî ïðîòèâîïîëîæíîå íàïðÿæåíèå íàçûâàåòñÿ ÝëåêòðîÄâèæóùåéÑèëîé ñàìîèíäóêöèè, èëè ïðîñòî — ÝÄÑ ñàìîèíäóêöèè. Ýòî ÝÄÑ çàâèñèò îò èíäóêòèâíîñòè êàòóøêè. Ïîýòîìó â ìîìåíò ïîäà÷è íàïðóãè íà êàòóøêó Ñèëà òîêà â òå÷åíèå äîëåé ñåêóíä ïëàâíî ìåíÿåò ñâîå çíà÷åíèå îò 0 äî íåêîòîðîãî çíà÷åíèÿ, ïîòîìó ÷òî íàïðÿæåíèå,â ìîìåíò ïîäà÷è ýëåêòðè÷åñêîãî òîêà, òàêæå ìåíÿåò ñâîå çíà÷åíèå îò íîëÿ è äî óñòàíîâèâøåãîñÿ çíà÷åíèÿ, ñîãëàñíî Çàêîí Îìà:
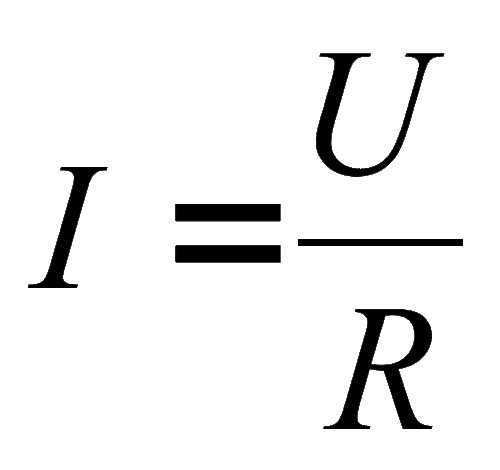
ãäå I — ñèëà òîêà â êàòóøêå, U — íàïðÿæåíèå â êàòóøêå, R — ñîïðîòèâëåíèå êàòóøêè.
Êàê ìû âèäèì ïî ôîðìóëå, íàïðÿæåíèå ìåíÿåòñÿ îò íóëÿ è äî íàïðÿæåíèÿ, ïîäàâàåìîãî â êàòóøêó, ñëåäîâàòåëüíî è òîê òîæå áóäåò ìåíÿòüñÿ îò íóëÿ è äî êàêîãî òî çíà÷åíèÿ. Ñîïðîòèâëåíèå êàòóøêè ïîñòîÿííîå.
È âòîðîé ïðèêîë â êàòóøêå èíäóêòèâíîñòè çàêëþ÷àåòñÿ â òîì, ÷òî åñëè ìû ðàçîìêíåì öåïü êàòóøêà èíäóêòèâíîñòè — èñòî÷íèê òîêà, òî ó íàñ ÝÄÑ ñàìîèíäóêöèè áóäåò ïðèïëþñîâûâàòüñÿ ê íàïðÿæåíèþ, êîòîðîå ìû ïîäàëè íà êàòóøêó. Ñëåäîâàòåëüíî è òîê áóäåò â ñàìîì íà÷àëå áîëüøå, à ïîòîì òèõîíüêî ñïàäåò äî íóëÿ. Âðåìÿ ñïàäà ñèëû òîêà òàêæå çàâèñèò îò èíäóêòèâíîñòè êàòóøêè.
Ñäåëàåì ïåðâûå âûâîäû î ðàáîòå êàòóøêè èíäóêòèâíîñòè ïðè ïîäà÷å íà íåå ïîñòîÿííîãî òîêà. Ïðè ïîäà÷å íà êàòóøêó ýëåêòðè÷åñêîãî òîêà, ñèëà òîêà áóäåò ïëàâíî óâåëè÷èâàòüñÿ, à ïðè ñíÿòèè ýëåêòðè÷åñêîãî òîêà ñ êàòóøêè, ñèëà òîêà ðåçêî âîçðàñòåò â êàòóøêå è ïëàâíî óáàâèòüñÿ äî íóëÿ. Êîðî÷å ãîâîðÿ,ñèëà òîêà â êàòóøêå ìãíîâåííî èçìåíèòüñÿ íå ìîæåò. Ýòî â ýëåêòðîíèêå íàçûâàþò ïåðâûì çàêîíîì êîììóòàöèè. Óôô, íó âñå, ñàìîå òÿæåëîå ïîçàäè :-).
Êàòóøêè èíäóêòèâíîñòè äåëÿòñÿ â îñíîâíîì íà äâà êëàññà: ñ ìàãíèòíûì è íåìàãíèòíûì ñåðäå÷íèêîì. Ñíèçó íà ôîòî êàòóøêà ñ íåìàãíèòíûì ñåðäå÷íèêîì.

Íî ãäå ó íåå ñåðäå÷íèê? Âîçäóõ — ýòî íåìàãíèòíûé ñåðäå÷íèê :-). Òàêèå êàòóøêè òàêæå ìîãóò áûòü íàìîòàíû íà êàêîé-íèáóäü öèëèíäðè÷åñêîé áóìàæíîé òðóáî÷êå. Èíäóêòèâíîñòü êàòóøåê ñ íåìàãíèòíûì ñåðäå÷íèêîì èñïîëüçóåòñÿ, êîãäà èíäóêòèâíîñòü íå ïðåâûøàåò 5 ìèëëèÃåíðè.
À âîò êàòóøêè èíäóêòèâíîñòè ñ ñåðäå÷íèêîì:

 îñíîâíîì èñïîëüçóþò ñåðäå÷íèêè èç ôåððèòà è æåëåçíûõ ïëàñòèí. Ñåðäå÷íèêè ïîâûøàþò èíäóêòèâíîñòü êàòóøåê â ðàçû. Ñåðäå÷íèêè â âèäå êîëüöà (òîðîèäàëüíûå) ïîçâîëÿþò ïîëó÷èòü áîëüøóþ èíäóêòèâíîñòü, íåæåëè ïðîñòî ñåðäå÷íèêè èç öèëèíäðà.
Äëÿ êàòóøåê ñðåäíåé èíäóêòèâíîñòè èñïîëüçóþòñÿ ôåððèòîâûå ñåðäå÷íèêè:

Êàòóøêè ñ áîëüøîé èíäóêòèâíîñòüþ äåëàþò êàê òðàíñôîðìàòîð ñ æåëåçíûì ñåðäå÷íèêîì, íî åñòü îäíî ðàçëè÷èå: ó íèõ èìååòñÿ òîëüêî îäíà ïåðâè÷íàÿ îáìîòêà:

Îò êàêèõ ôàêòîðîâ çàâèñèò èíäóêòèâíîñòü êàòóøêè? Äàâàéòå ïðîâåäåì íåñêîëüêî îïûòîâ. ß íàìîòàë êàòóøêó ñ íåìàãíèòíûì ñåðäå÷íèêîì. Åå èíäóêòèâíîñòü íàñòîëüêî ìàëà, ÷òî LC — ìåòð ìíå ïîêàçûâàåò íîëü.

Èìååòñÿ ôåððèòîâûé ñåðäå÷íèê

Íà÷èíàþ ââîäèòü êàòóøêó â ñåðäå÷íèê íà ñàìûé êðàé

LC-ìåòð ïîêàçûâàåò 21 ìèêðîÃåíðè.
Ââîæó êàòóøêó íà ñåðåäèíó ôåððèòà

35 ìèêðîÃåíðè. Óæå ëó÷øå.
Ïðîäîëæàþ ââîäèòü êàòóøêó íà ïðàâûé êðàé ôåððèòà

20 ìèêðîÃåíðè. Äåëàåì âûâîä, ñàìàÿ áîëüøàÿ èíäóêòèâíîñòü íà öèëèíäðè÷åñêîì ôåððèòå âîçíèêàåò â åãî ñåðåäèíå. Ïîýòîìó, åñëè áóäåòå ìîòàòü íà öèëèíäðèêå, ñòàðàéòåñü ìîòàòü â ñåðåäèíå ôåððèòà. Ýòî ñâîéñòâî èñïîëüçóåòñÿ äëÿ ïëàâíîãî èçìåíåíèÿ èíäóêòèâíîñòè â ïåðåìåííûõ êàòóøêàõ èíäóêòèâíîñòè:
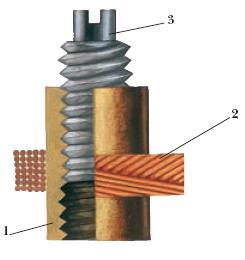
ãäå
1 — ýòî êàðêàñ êàòóøêè
2 — ýòî âèòêè êàòóøêè
3 — ñåðäå÷íèê, ó êîòîðîãî ñâåðõó ïàçèê ïî ìàëåíüêóþ îòâåðòêó. Âêðó÷èâàÿ èëè âûêðó÷èâàÿ ñåðäå÷íèê, ìû òåì ñàìûì èçìåíÿåì èíäóêòèâíîñòü êàòóøêè.
Ýêñïåðèìåíòèðóåì äàëüøå. Äàâàéòå ïîïðîáóåì ñæèìàòü è ðàçæèìàòü âèòêè êàòóøêè. Äëÿ íà÷àëà ñòàâèì åå â ñåðåäèíó è íà÷èíàåì ñæèìàòü âèòêè

Èíäóêòèâíîñòü ñòàëà ïî÷òè 50 ìèêðîÃåíðè!
À äàâàéòå-êà ïîïðîáóåì ðàñïðàâèì âèòêè ïî âñåìó ôåððèòó

13 ìèêðîÃåíðè. Äåëàåì âûâîä: äëÿ ìàêñèìàëüíîé èíäóêòèâíîñòè ìîòàòü êàòóøêó íàäî «âèòîê ê âèòêó».
Óáàâèì âèòêè êàòóøêè â äâà ðàçà. Áûëî 24 âèòêà, ñòàëî 12.

Ñîâñåì ìàëåíüêàÿ èíäóêòèâíîñòü. Óáàâèë êîëè÷åñòâî âèòêîâ â 2 ðàçà, èíäóêòèâíîñòü óìåíüøèëàñü â 10 ðàç. Âûâîä: ÷åì ìåíüøå êîëè÷åñòâî âèòêîâ — òåì ìåíüøå èíäóêòèâíîñòü. Èíäóêòèâíîñòü ìåíÿåòñÿ íå ïðÿìîëèíåéíî âèòêàì.
Äàâàéòå ïîýêñïåðèìåíòèðóåì ñ ôåððèòîâûì êîëüöîì.

Çàìåðÿåì èíäóêòèâíîñòü

15 ìèêðîÃåíðè
Îòäàëèì âèòêè êàòóøêè äðóã îò äðóãà

Çàìåðÿåì ñíîâà

Õì, òàêæå 15 ìèêðîÃåíðè. Äåëàåì âûâîä: ðàññòîÿíèå îò âèòêà äî âèòêà íå èãðàåò íèêàêîé ðîëè êàòóøêè èíäóêòèâíîñòè â òîðîèäàëüíîì ñåðäå÷íèêå.
Ìîòàíåì ïîáîëüøå âèòêîâ. Áûëî 3 âèòêà, ñòàëî 9.

Çàìåðÿåì

Îôèãåòü! Óâåëè÷èë êîëè÷åñòâî âèòêîâ â 3 ðàçà, à èíäóêòèâíîñòü óâåëè÷èëàñü â 12 ðàç! Âûâîä: èíäóêòèâíîñòü ìåíÿåòñÿ íå ïðÿìîëèíåéíî âèòêàì.
Åñëè âåðèòü ôîðìóëàì äëÿ ðàñ÷åòà èíäóêòèâíîñòåé, èíäóêòèâíîñòü çàâèñèò îò «âèòêîâ â êâàäðàòå». Ýòè ôîðìóëû ÿ çäåñü âûêëàäûâàòü íå áóäó, ïîòîìó êàê íå âèæó íàäîáíîñòè. Ñêàæó òîëüêî, ÷òî èíäóêòèâíîñòü çàâèñèò åùå îò òàêèõ ïàðàìåòðîâ, êàê ñåðäå÷íèê (èç êàêîãî ìàòåðèàëà îí ñäåëàí), ïëîùàäü ïîïåðå÷íîãî ñå÷åíèÿ ñåðäå÷íèêà, äëèíà êàòóøêè. Îñòàëüíûå ôàêòîðû ìû ðàçîáðàëè â îïûòàõ. Áîëåå ïîäðîáíî ïðî ôîðìóëû ðàñ÷åòà çäåñü. Íî ëó÷øå âñå òàêè èçãîòîâèòü êàòóøêó îïûòíûì ïóòåì ñ çàìåðîì åå èíäóêòèâíîñòè íà êàæäîì ýòàïå.
Íà ñõåìàõ êàòóøêè èíäóêòèâíîñòè îáîçíà÷àþòñÿ âîò òàê:
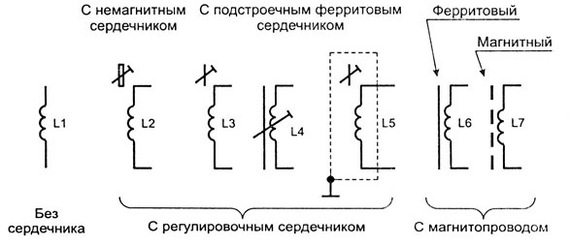
Ïðè ïîñëåäîâàòåëüíîì ñîåäèíåíèè èíäóêòèâíîñòåé, èõ îáùàÿ èíäóêòèâíîñòü ðàâíà ñóììå èíäóêòèâíîñòåé.
Lîáù=L1+L2+…+Ln
À ïðè ïàðàëëåëüíîì ñîåäèíåíèè ïîëó÷àåì âîò òàê:
1/Lîáù=1/L1+1/L2+…1/Ln
Ïðè ñîåäèíåíèè èíäóêòèâíîñòåé äîëæíî âûïîëíÿòüñÿ ïðàâèëî, ÷òîáû îíè áûëè ïðîñòðàíñòâåííî ðàçíåñåíû íà ïëàòå. Ýòî ñâÿçàíî ñ òåì, ÷òî ïðè áëèçêîì ðàñïîëîæåíèè äðóã äðóãà èõ ìàãíèòíûå ïîëÿ áóäóò âëèÿòü ñ äðóã äðóãîì, è ïîýòîìó ïîêàçàíèÿ èíäóêòèâíîñòåé áóäóò íåïðàâèëüíû. Íå ñòàâüòå íà îäíó æåëåçíóþ îñüêó äâà è áîëåå òîðîèäàëüíûõ êàòóøåê, ýòî ìîæåò ïðèâåñòè ê íåïðàâèëüíûì ïîêàçàíèÿì îáùåé èíäóêòèâíîñòè.
Òàêæå åñòü îñîáûé âèä êàòóøåê èíäóêòèâíîñòåé. Ýòî òàê íàçûâàåìûå äðîññåëè. Äðîññåëü — ýòî êàòóøêà èíäóêòèâíîñòè, çàäà÷à êîòîðîé ñîçäàòü â öåïè áîëüøîå ñîïðîòèâëåíèå äëÿ ïåðåìåííîãî òîêà, ÷òîáû ïîäàâèòü òîêè âûñîêèõ ÷àñòîò. ×àùå âñåãî äðîññåëè ïðèìåíÿþòñÿ â ôèëüòðàõ èñòî÷íèêîâ ïèòàíèÿ.
Êàòóøêà èíäóêòèâíîñòè èãðàåò â ýëåêòðîíèêå î÷åíü áîëüøóþ ðîëü, îñîáåííî â ïðèåìî-ïåðåäàþùåé àïïàðàòóðå. Íà êàòóøêàõ èíäóêòèâíîñòè ñòðîÿòñÿ òàêæå ðàçëè÷íûå ôèëüòðû äëÿ ýëåêòðîííîé ðàäèîàïïàðàòóðû, à â ýëåêòðîòåõíèêå åå èñïîëüçóþò òàêæå â êà÷åñòâå
ÇÛ: Âçÿë ãäå âçÿë, îáîáùèë è äîáàâèë íåìíîãî.
Áåðåãèòå ñåáÿ è ñâîèõ áëèçêèõ!
Èñòî÷íèê: https://www.ruselectronic.com/news/katushka-induktivnosti/
