Каким свойством обладает касательная к окружности
Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.
Понятие касательной к окружности и основные свойства касательной проиллюстрированы ниже на рисунке.
. Угол равен , где — центр окружности. Его сторона касается окружности. Найдите величину меньшей дуги окружности, заключенной внутри этого угла. Ответ дайте в градусах.
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Значит, угол — прямой. Из треугольника получим, что угол равен градуса. Величина центрального угла равна угловой величине дуги, на которую он опирается, значит, величина дуги — тоже градуса.
Ответ: .
. Найдите угол , если его сторона касается окружности, — центр окружности, а большая дуга окружности, заключенная внутри этого угла, равна . Ответ дайте в градусах.
Это чуть более сложная задача. Центральный угол опирается на дугу , следовательно, он равен градусов. Тогда угол равен . Касательная перпендикулярна радиусу, проведенному в точку касания, значит, угол — прямой. Тогда угол равен .
Ответ: .
. Хорда стягивает дугу окружности в . Найдите угол между этой хордой и касательной к окружности, проведенной через точку . Ответ дайте в градусах.
Проведем радиус в точку касания, а также радиус . Угол равен . Треугольник — равнобедренный. Нетрудно найти, что угол равен градуса, и тогда угол равен градусов, то есть половине угловой величины дуги .
Получается, что угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.
. К окружности, вписанной в треугольник , проведены три касательные. Периметры отсеченных треугольников равны , , . Найдите периметр данного треугольника.
Вспомним еще одно важное свойство касательных к окружности:
Отрезки касательных, проведенных из одной точки, равны.
Периметр треугольника — это сумма всех его сторон. Обратите внимание на точки на нашем чертеже, являющиеся вершинами шестиугольника. Из каждой такой точки проведены два отрезка касательных к окружности. Отметьте на чертеже такие равные отрезки. Еще лучше, если одинаковые отрезки вы будете отмечать одним цветом. Постарайтесь увидеть, как периметр треугольника складывается из периметров отсеченных треугольников.
Ответ: .
Вот более сложная задача из вариантов ЕГЭ:
. Около окружности описан многоугольник, площадь которого равна . Его периметр равен . Найдите радиус этой окружности.
Обратите внимание — в условии даже не сказано, сколько сторон у этого многоугольника. Видимо, это неважно. Пусть их будет пять, как на рисунке.
Окружность касается всех сторон многоугольника. Отметьте центр окружности — точку — и проведите перпендикулярные сторонам радиусы в точки касания.
Соедините точку с вершинами . Получились треугольники и .
Очевидно, что площадь многоугольника .
Как вы думаете, чему равны высоты всех этих треугольников и как, пользуясь этим, найти радиус окружности?
Ответ: .
Мы используем файлы cookie, чтобы персонализировать контент, адаптировать и оценивать результативность рекламы, а также обеспечить безопасность. Перейдя на сайт, вы соглашаетесь с использованием файлов cookie.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Окружность
- Касательная к окружности
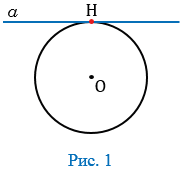
Касательная к окружности — прямая, имеющая с окружностью одну общую точку, которая называется точкой касания прямой и окружности. На рисунке 1 прямая — касательная к окружности, точка Н — точка касания прямой и окружности с центром в точке О.
Свойство касательной к окружности
Теорема
Доказательство
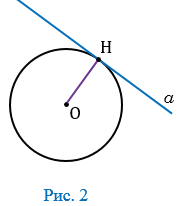
Дано: — касательная к окружности с центром в точке О, Н — точка касания (Рис. 2).
Доказать: ОН
.
Доказательство:
Предположим, что ОН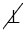
. Тогда радиус ОН является наклонной к прямой . При этом перпендикуляр, проведенный из точки О к прямой , меньше наклонной ОН, тогда расстояние от центра О окружности до прямой меньше радиуса. Следовательно прямая и окружность будут иметь две общие точки, что противоречит условию: прямая — касательная. Поэтому наше предположение неверно, значит, ОН . Теорема доказана.
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Доказательство
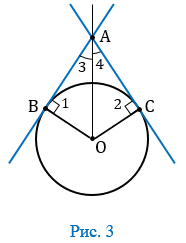
Дано: АВ и АС — касательные к окружности с центром в точке О, В и С — точки касания (Рис. 3).
Доказать: АВ = АС и 
3 =4.
Доказательство:
1 =2 = 900, т.к. ОВАВ, ОСАС по теореме о свойстве касательной (смотри выше), поэтому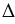 
АВО и 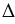АСО прямоугольные. При этом ОВ = ОС (радиусы), АО — общая, следовательн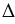о, АВО =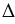АСО (по гипотенузе и катету). Из равенства треугольников следует, что АВ = АС и 3 =4. Что и требовалось доказать.
Теорема, обратная теореме о свойстве касательной (признак касательной)
Теорема
Доказательство
Дано: ОН — радиус окружности с центром в точке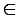 О, Н
, ОН (Рис. 4).
Доказать: — касательная.
Доказательство:
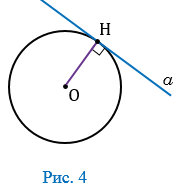
По условию радиус ОН , поэтому расстояние от центра окружности до прямой равно радиусу, и, следовательно, прямая и окружность имеют только одну общую точку, значит, данная прямая является касательной к окружности (по определению касательной). Теорема доказана.
Задача
Через данную точку А окружности с центром О провести касательную к этой окружности.
Дано: точка А лежит на окружности с центром в точке О.
Провести касательную к окружности так, что А.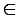
Решение:
Строим с помощью циркуля окружность с центром в точкеО, отмечаем на данной окружности точку А.
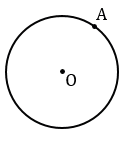
Далее проводим прямую ОА и строим прямую , проходящую через точку А перпендикулярно к прямой ОА. Для этого с помощью циркуля строим окружность произвольного радиуса с центром в точке А (всю окружность строить необязательно, смотри выделенное красным). Точки пересечения данной окружности с прямой ОА обозначаем буквами В и С.
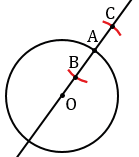
Затем строим две окружности радиуса ВС с центрами в точках В и С (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Данные окружности пересекаются в двух точках, обозначим их Р и Q. Через точки Р и Q с помощью линейки проводим прямую , которая будет перпендикулярна к прямой ОА.
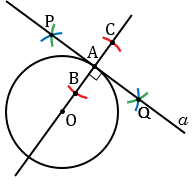
Итак, ОА, ОА — радиус, следовательно, — искомая касательная к окружности с центром в точке О радиуса ОА (по признаку касательной).
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Взаимное расположение прямой и окружности
Градусная мера дуги окружности
Теорема о вписанном угле
Свойство биссектрисы угла
Свойства серединного перпендикуляра к отрезку
Теорема о пересечении высот треугольника
Вписанная окружность
Описанная окружность
Окружность
Правило встречается в следующих упражнениях:
7 класс
Задание 636,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 638,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 643,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 644,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 664,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 677,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 21,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 725,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 737,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 892,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
§ 20. Некоторые свойства окружности. Касательная к окружности
Теорема 20.1
Диаметр окружности, перпендикулярный хорде, делит эту хорду пополам.
Рис. 287 |
|
Доказательство
Если хорда является диаметром, то теорема очевидна.
На рисунке 287 изображена окружность с центром O, M — точка пересечения диаметра CD и хорды AB, CD ⊥ AB. Надо доказать, что AM = MB.
Проведём радиусы OA и OB. В равнобедренном треугольнике AOB (OA = OB) отрезок OM — высота, а значит, и медиана, т. е. AM = MB. 
Теорема 20.2
Диаметр окружности, делящий хорду, отличную от диаметра, пополам, перпендикулярен этой хорде.
Докажите эту теорему самостоятельно. Подумайте, будет ли верным это утверждение, если хорда является диаметром.
На рисунке 288 показаны все возможные случаи взаимного расположения прямой и окружности. На рисунке 288, а они не имеют общих точек, на рисунке 288, б — имеют две общие точки, на рисунке 288, в — одну.
Определение
Прямую, имеющую с окружностью только одну общую точку, называют касательной к окружности.
Касательная к окружности имеет только одну общую точку с кругом, ограниченным этой окружностью. На рисунке 288, в прямая a — касательная к кругу с центром в точке O, A — точка касания.
Если отрезок (луч) принадлежит касательной к окружности и имеет с этой окружностью общую точку, то говорят, что отрезок (луч) касается окружности. Например, на рисунке 289 изображён отрезок AB, который касается окружности в точке С.
Теорема 20.3
(свойство касательной)
Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
Доказательство
На рисунке 290 изображена окружность с центром O, A — точка касания прямой a и окружности. Надо доказать, что OA ⊥ a.
Рис. 289 | Рис. 290 | Рис. 291 |
|
|
|
Предположим, что это не так, т. е. отрезок OA — наклонная к прямой a. Тогда из точки O опустим перпендикуляр OM на прямую a (рис. 291). Поскольку точка A — единственная общая точка прямой a и круга с центром O, то точка M не принадлежит этому кругу. Отсюда OM = MB + OB, где точка B — точка пересечения окружности и перпендикуляра OM. Отрезки OA и OB равны как радиусы окружности. Таким образом, OM > OA. Получили противоречие: перпендикуляр OM больше наклонной OA. Следовательно, OA ⊥ a. 
Теорема 20.4
(признак касательной к окружности)
Если прямая, проходящая через точку окружности, перпендикулярна радиусу, проведённому в эту точку, то эта прямая является касательной к данной окружности.
Доказательство
Рис. 292 |
|
На рисунке 290 изображена окружность с центром в точке O, отрезок OA — её радиус, точка A принадлежит прямой a, OA ⊥ a. Докажем, что прямая a — касательная к окружности.
Пусть прямая a не является касательной, а имеет ещё одну общую точку B с окружностью (рис. 292). Тогда ∆AOB — равнобедренный (OA = OB как радиусы). Отсюда ∠OBA = ∠OAB = 90°. Получаем противоречие: в треугольнике AOB есть два прямых угла. Следовательно, прямая a является касательной к окружности. 
Следствие
Если расстояние от центра окружности до некоторой прямой равно радиусу окружности, то эта прямая является касательной к данной окружности.
Рис. 293 |
|
Докажите это следствие самостоятельно.
Задача. Докажите, что если через данную точку к окружности проведены две касательные, то отрезки касательных, соединяющих данную точку с точками касания, равны.
Решение. На рисунке 293 изображена окружность с центром O. Прямые AB и AC — касательные, точки B и C — точки касания. Надо доказать, что AB = AC.
Проведём радиусы OB и OC в точки касания. По свойству касательной OB ⊥ AB и OC ⊥ AC. В прямоугольных треугольниках AOB и AOC катеты OB и OC равны как радиусы одной окружности, AO — общая гипотенуза. Следовательно, треугольники AOB и AOC равны по гипотенузе и катету. Отсюда AB = AC. 
- Как делит хорду диаметр, перпендикулярный ей?
- Чему равен угол между хордой, отличной от диаметра, и диаметром, делящим эту хорду пополам?
- Опишите все возможные случаи взаимного расположения прямой и окружности.
- Какую прямую называют касательной к окружности?
- Каким свойством обладает радиус, проведённый в точку касания прямой и окружности?
- Сформулируйте признак касательной к окружности.
- Каким свойством обладают касательные, проведённые к окружности через одну точку?
Практические задания
507.Начертите окружность с центром O, проведите хорду AB. Пользуясь угольником, разделите эту хорду пополам.
508.Начертите окружность с центром O, проведите хорду CD. Пользуясь линейкой со шкалой, проведите диаметр, перпендикулярный хорде CD.
509.Начертите окружность, отметьте на ней точки A и B. Пользуясь линейкой и угольником, проведите прямые, которые касаются окружности в точках A и B.
510.Проведите прямую a и отметьте на ней точку M. Пользуясь угольником, линейкой и циркулем, проведите окружность радиуса 3 см, которая касается прямой a в точке M. Сколько таких окружностей можно провести?
Упражнения
511.На рисунке 294 точка O — центр окружности, диаметр CD перпендикулярен хорде AB. Докажите, что ∠AOD = ∠BOD.
512.Докажите, что равные хорды окружности равноудалены от её центра.
513.Докажите, что если хорды окружности равноудалены от её центра, то они равны.
514.Верно ли, что прямая, перпендикулярная радиусу окружности, касается этой окружности?
515.Прямая CD касается окружности с центром O в точке A, отрезок AB — хорда окружности, ∠BAD = 35° (рис. 295). Найдите ∠AOB.
516.Прямая CD касается окружности с центром O в точке A, отрезок AB — хорда окружности, ∠AOB = 80° (см. рис. 295). Найдите ∠BAC.
517.Дана окружность, диаметр которой равен 6 см. Прямая a удалена от её центра на: 1) 2 см; 2) 3 см; 3) 6 см. В каком случае прямая a является касательной к окружности?
518.В треугольнике ABC известно, что ∠C = 90°. Докажите, что:
1)прямая BC является касательной к окружности с центром A, проходящей через точку C;
2)прямая AB не является касательной к окружности с центром C, проходящей через точку A.
519.Докажите, что диаметр окружности больше любой хорды, отличной от диаметра.
520.В окружности с центром O через середину радиуса провели хорду AB, перпендикулярную ему. Докажите, что ∠AOB = 120°.
521.Найдите угол между радиусами OA и OB окружности, если расстояние от центра O окружности до хорды AB в 2 раза меньше: 1) длины хорды AB; 2) радиуса окружности.
522.В окружности провели диаметр AB и хорды AC и CD так, что AC = 12 см, ∠BAC = 30°, AB ⊥ CD. Найдите длину хорды CD.
523.Через точку M к окружности с центром O провели касательные MA и MB, A и B — точки касания, ∠OAB = 20°. Найдите ∠AMB.
524.Через концы хорды AB, равной радиусу окружности, провели две касательные, пересекающиеся в точке C. Найдите ∠ACB.
525.Через точку C окружности с центром O провели касательную к этой окружности, AB — диаметр окружности. Из точки A на касательную опущен перпендикуляр AD. Докажите, что луч AC — биссектриса угла BAD.
526.Прямая AC касается окружности с центром O в точке A (рис. 296). Докажите, что угол BAC в 2 раза меньше угла AOB.
Рис. 294 | Рис. 295 | Рис. 296 |
|
|
|
527.Отрезки AB и BC — соответственно хорда и диаметр окружности, ∠ABC = 30°. Через точку A провели касательную к окружности, пересекающую прямую BC в точке D. Докажите, что ∆ABD — равнобедренный.
528.Известно, что диаметр AB делит хорду CD пополам, но не перпендикулярен ей. Докажите, что CD — также диаметр.
529.Найдите геометрическое место центров окружностей, которые касаются данной прямой в данной точке.
530.Найдите геометрическое место центров окружностей, которые касаются обеих сторон данного угла.
531.Найдите геометрическое место центров окружностей, которые касаются данной прямой.
532.Прямые, касающиеся окружности с центром O в точках A и B, пересекаются в точке K, ∠AKB = 120°. Докажите, что AK + BK = OK.
533.Окружность касается стороны AB треугольника ABC в точке M и касается продолжения двух других сторон. Докажите, что сумма длин отрезков BC и BM равна половине периметра треугольника ABC.
Рис. 297 |
|
534.Через точку C проведены касательные AC и BC к окружности, A и B — точки касания (рис. 297). На окружности взяли произвольную точку M, лежащую в одной полуплоскости с точкой C относительно прямой AB, и через неё провели касательную к окружности, пересекающую прямые AC и BC в точках D и E соответственно. Докажите, что периметр треугольника DEC не зависит от выбора точки M.
Упражнения для повторения
535.Докажите, что середина M отрезка, концы которого принадлежат двум параллельным прямым, является серединой любого отрезка, который проходит через точку M и концы которого принадлежат этим прямым.
536.Отрезки AB и CD лежат на одной прямой и имеют общую середину. Точку M выбрали так, что треугольник AMB — равнобедренный с основанием AB. Докажите, что ∆CMD также является равнобедренным с основанием CD.
537.На стороне MK треугольника MPK отметили точки E и F так, что точка E лежит между точками M и F, ME = EP, PF = FK. Найдите угол M, если ∠EPF = 92°, ∠K = 26°.
538.В остроугольном треугольнике ABC проведена биссектриса BM, из точки M на сторону BC опущен перпендикуляр MK, ∠ABM = ∠KMC. Докажите, что треугольник ABC — равнобедренный.
Наблюдайте, рисуйте, конструируйте, фантазируйте
539.Установите закономерность форм фигур, изображённых на рисунке 298. Какую фигуру надо поставить следующей?
Рис. 298 |
|
Касательная прямая к окружности в евклидовой геометрии на плоскости — прямая, которая имеет с окружностью ровно одну общую точку. Также можно определить касательную как предельное положение секущей, когда точки пересечения её с окружностью бесконечно сближаются. Касательные прямые к окружностям служат предметом рассмотрения ряда теорем и играют важную роль во многих геометрических построениях и доказательствах.
Касательные прямые к одной окружности[править | править код]
Касательная прямая t к окружности C пересекает окружность в единственной точке T. Для сравнения, секущие прямые пересекают окружность в двух точках, в то время как некоторые прямые могут не пересекать окружность совсем. Это свойство касательной прямой сохраняется при многих геометрических преобразованиях[en], таких как подобие, вращение, параллельный перенос, инверсия и картографическая проекция. Говоря техническим языком, эти преобразования не меняют структуру инцидентности касательных прямых и окружностей, даже если сами прямые и окружности деформируются.
Радиус окружности, проведённый через точку касания, перпендикулярен касательной прямой. И обратно, перпендикуляр к радиусу в конечной точке (на окружности) является касательной прямой. Окружность вместе с касательной прямой имеют осевую симметрию относительно радиуса (к точке касания).
По теореме о степени точки произведение длин PM•PN для любого луча PMN равно квадрату PT, длине отрезка от точки P до точки касания (отрезок показан красным цветом).
Никакая касательная прямая не может проходить через точку внутри окружности, поскольку любая такая прямая должна быть секущей. В то же время для любой точки, лежащей вне круга, можно построить две проходящие через неё касательные прямые. Геометрическая фигура, состоящая из окружности и двух касательных прямых, также обладает осевой симметрией относительно прямой, соединяющей точку P с центром окружности O (см. рисунок справа). В этом случае отрезки от точки P до двух точек касания имеют одинаковую длину. По теореме о степени точки квадрат длины отрезка до точки касания равен степени точки P относительно окружности C. Эта степень равна произведению расстояний от точки P до двух точек пересечения окружности любой секущей линией, проходящей через P.
Угол θ между хордой и касательной равен половине дуги, заключённой между концами хорды.
Касательная прямая t и точка касания T обладают свойством сопряжённости друг другу; это соответствие можно обобщить в идею о полюсе и поляре. Такая же взаимосвязь существует между точкой P вне окружности и секущей линией, соединяющей две точки касания.
Если точка P лежит вне окружности с центром O, и если касательные прямые из P касаются окружности в точках T и S, то углы ∠TPS и ∠TOS дают в сумме 180°.
Если хорда TM проведена из точки касания T прямой P T и ∠PTM ≤ 90°, то ∠PTM = (1/2)∠MOT.
Геометрическое построение[править | править код]
Построение касательной прямой к окружности (выделена красным) перпендикулярно радиусу.
Относительно легко построить прямую t, касательную к окружности в точке T на окружности. Для этого следует провести прямую a через центр окружности O и точку T. Тогда прямая t является перпендикуляром к прямой a. Один из способов построения перпендикуляра следующий (см. рисунок). Проводим тем же радиусом (r) окружность с центром в точке T, получаем вторую точку G на прямой a, а точка T становится серединой отрезка OG. Проводим две окружности радиуса R>r с центрами в точках O и G. Прямая, проходящая через точки пересечения этих окружностей, будет касательной.
Построение касательной прямой к окружности
Для построения касательной прямой через точку P к окружности C можно использовать свойство угла, опирающегося на диаметр окружности. Проводится окружность с центром в точке H, середине отрезка OP, где O — центр окружности C. Пересечения T и T‘ являются точками касания прямых, проходящих через точку P, поскольку углы ∠OTP и ∠OT‘P опираются на диаметр OP окружности с центром в H.
Теорема об описанном четырёхугольнике и вписанные окружности[править | править код]
Описанный четырёхугольник ABCD — это замкнутая фигура с четырьмя сторонами, которые касаются окружности C. Соответственно, C — вписанная в четырёхугольник ABCD окружность. По теореме Пито суммы противоположных сторон любого такого четырёхугольника равны, то есть
Описанный четырёхугольник
Это заключение следует из равенства отрезков касательных от вершин четырёхугольника. Обозначим точки касания как P (на отрезке AB), Q (на отрезке BC), R (на отрезке CD) и S (на отрезке DA). Симметричные отрезки до точек касания от каждой вершины четырёхугольника ABCD равны, то есть BP=BQ=b, CQ=CR=c, DR=DS=d и AS=AP=a.
Но каждая сторона четырёхугольника состоит из двух таких отрезков
,
что и доказывает утверждение.
Обратное утверждение также верно — окружность можно вписать в любой выпуклый четырёхугольник, у которого суммы длин противоположных сторон равны.[1]
Эта теорема и обратная к ней имеют различные применения. Например, из теоремы немедленно следует, что ни в какой прямоугольник не может быть вписана окружность, если только это не квадрат, а также что можно вписать окружность в любой ромб, хотя в общем случае вписать в параллелограмм окружность нельзя.
Касательные прямые к двум окружностям[править | править код]
Внешний (сверху) и внутренний (внизу) центры гомотетии двух окружностей (выделены красным цветом), показанные зелёными точками.
Для двух окружностей в общем случае имеется четыре различные прямые, касательные к обоим окружностям, если одна окружность не лежит в другой, но в вырожденных случаях может быть любое число касательных от нуля до четырёх. Эти случаи описаны ниже. Из четырёх касательных прямых две являются внешними касательными, когда окружности оказываются лежащими по одну сторону от касательной прямой. Для двух других прямых, внутренних касательных, окружности оказываются лежащими по разные стороны от касательной прямой. Внешние касательные пересекаются в центре внешней гомотетии[en], в то время как внутренние касательные пересекаются в центре внутренней гомотетии. И внутренний, и внешний центры гомотетии лежат на прямой, проходящей через центры окружностей, ближе к центру меньшей окружности. Если две окружности имеют одинаковые радиусы, остаются те же четыре касательных, но внешние касательные прямые параллельны и внешнего центра гомотетии на аффинной плоскости не существует. На проективной плоскости внешний центр гомотетии лежит в бесконечно удалённой точке, соответствующей пересечению прямых.[2]
Внешняя касательная[править | править код]
Построение внешних касательных.
Красные прямые, соединяющие точки T1 и T3, T2 и T4, являются внешними касательными двух окружностей.
Внутренняя касательная[править | править код]
Внутренние касательные — это касательные, которые пересекают отрезок, соединяющий центры окружностей. Заметим, что внутренние касательные не существуют в случае пересекающихся окружностей.
Построение[править | править код]
Построение внутренних касательных
Касательные к двум окружностям могут быть построены с помощью нахождения центров гомотетии, как описано выше, а затем построения касательных, проходящих через эти центры. Можно также построить касательные прямые и касательные точки прямо, как описано ниже.
Элементарная геометрия[править | править код]
Пусть O1 и O2 — два центра двух окружностей C1 и C2 и пусть r1 и r2 — их радиусы, при этом r1 > r2. Другими словами, окружность C1 будем считать большей из двух окружностей. Два различных способа можно использовать для построения внешних и внутренних касательных прямых.
Внешние касательные
Рисуем новую окружность C3 с радиусом r1 − r2 с центром в O1. Используя метод, описанный выше, проводим две касательные прямые из точки O2 к этой новой окружности. Эти прямые параллельны искомым касательным прямым, поскольку это соответствует уменьшению радиусов обеих окружностей C1 и C2 на одно и то же число r2, в результате чего окружность C2 превращается в точку. Через две точки касания на окружности C3 можно провести два луча из центра O1. Эти лучи пересекают C1 в искомых точках касания. Искомые касательные перпендикулярны этим радиальным лучам и могут быть построены, как показывалось выше.
Внутренние касательные
Рисуем новую окружность C3 с радиусом r1 + r2 с центром в O1. Используя метод, описанный выше, проводим две касательные прямые из точки O2 к этой новой окружности. Эти прямые параллельны искомым касательным прямым, поскольку это соответствует уменьшению радиуса окружности C2 до нуля с одновременным увеличением радиуса C1 на ту же константу r2. Два радиальных луча можно провести из центра O1 через точки касания на C3. Эти лучи пересекают C1 в искомых точках касания. Искомые внутренние касательные перпендикулярны радиальным лучам и пересекают лучи в найденных точках, так что их можно построить вышеуказанным методом.
Фактически это то же самое построение, что и для внешних касательных, если принять, что радиус меньшей окружности отрицателен.