Каким свойством обладает импульс тела
В повседневной жизни для того, чтобы охарактеризовать человека, совершающего спонтанные поступки, иногда используют эпитет «импульсивный». При этом некоторые люди даже не помнят, а значительная часть и вовсе не знает, с какой физической величиной связано это слово. Что скрывается под понятием «импульс тела» и какими свойствами он обладает? Ответы на эти вопросы искали такие великие ученые, как Рене Декарт и Исаак Ньютон.
Импульс тела: определение
Как и всякая наука, физика оперирует четко сформулированными понятиями. На данный момент принято следующее определение для величины, носящей название импульса тела: это векторная величина, которая является мерой (количеством) механического движения тела.

Предположим, что вопрос рассматривается в рамках классической механики, т. е. считается, что тело движется с обычной, а не с релятивистской скоростью, а значит, она хотя бы на порядок меньше скорости света в вакууме. Тогда модуль импульса тела рассчитывается по формуле 1 (см. фото ниже).
Таким образом, по определению, эта величина равна произведению массы тела на его скорость, с которой сонаправлен ее вектор.
В качестве единицы измерения импульса в СИ (Международной системе единиц) принимается 1 кг/м/с.
Откуда появился термин «импульс»
За несколько веков до того, как в физике появилось понятие количества механического движения тела, считалось, что причиной любого перемещения в пространстве является особая сила — импетус.
В 14 веке в это понятие внес коррективы Жан Буридан. Он предположил, что летящий булыжник обладает импетусом, прямо пропорциональным скорости, который был бы неизменным, если бы отсутствовало сопротивления воздуха. В то же время, по мнению этого философа, тела с большим весом обладали способностью «вмещать» больше такой движущей силы.
Дальнейшее развитие понятию, позднее названного импульсом, дал Рене Декарт, который обозначил его словами «количество движения». Однако он не учитывал, что скорость имеет направление. Именно поэтому выдвинутая им теория в некоторых случаях противоречила опыту и не нашла признания.

О том, что количество движения должно иметь еще и направление, первым догадался английский ученый Джон Валлис. Произошло это в 1668 году. Однако понадобилась еще пара лет, чтобы он сформулировал известный закон сохранения количества движения. Теоретическое доказательство этого факта, установленного эмпирическим путем, было дано Исааком Ньютоном, который использовал открытые им же третий и второй законы классической механики, названные его именем.
Импульс системы материальных точек
Рассмотрим сначала случай, когда речь идет о скоростях, намного меньших, чем скорость света. Тогда, согласно законам классической механики, полный импульс системы материальных точек представляет векторную величину. Он равен сумме произведений их масс на скорости (см. формулу 2 на картинке выше).
При этом за импульс одной материальной точки принимают векторную величину (формула 3), которая сонаправлена со скоростью частицы.
Если речь идет о теле конечного размера, то сначала его мысленно разбивают на малые части. Таким образом, снова рассматривается система материальных точек, однако ее импульс рассчитывают не обычным суммированием, а путем интегрирования (см. формулу 4).
Как видим, временная зависимость отсутствует, поэтому импульс системы, на которую не воздействуют внешние силы (или их влияние взаимно компенсировано), остается неизменным во времени.

Доказательство закона сохранения
Продолжим рассматривать тело конечного размера как систему материальных точек. Для каждой из них Второй закон Ньютона формулируется согласно формуле 5.
Обратим внимание на то, что система замкнутая. Тогда, суммируя по всем точкам и применяя Третий закон Ньютона, получаем выражение 6.
Таким образом, импульс замкнутой системы является постоянной величиной.
Закон сохранения справедлив и в тех случаях, когда полная сумма сил, которые действуют на на систему извне, равна нулю. Отсюда следует одно важное частное утверждение. Оно гласит, что импульс тела является постоянной величиной, если воздействие извне отсутствует или влияние нескольких сил скомпенсировано. Например, в отсутствие трения после удара клюшкой шайба должна сохранять свой импульс. Такая ситуация будет наблюдаться даже невзирая на то, что на это тело действуют сила тяжести и реакции опоры (льда), так как они, хотя и равны по модулю, однако направлены в противоположные стороны, т. е. компенсируют друг друга.
Свойства
Импульс тела или материальной точки является аддитивной величиной. Что это значит? Все просто: импульс механической системы материальных точек складывается из импульсов всех входящих в систему материальных точек.
Второе свойство этой величины заключается в том, что она остается неизменной при взаимодействиях, которые изменяют лишь механические характеристики системы.
Кроме того, импульс инвариантен по отношению к любому повороту системы отсчета.
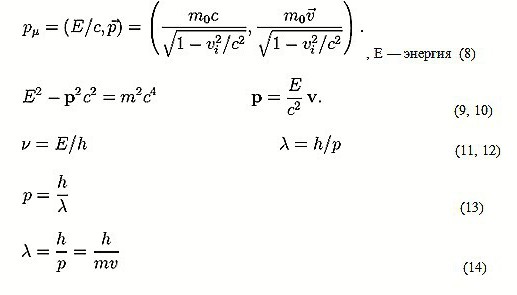
Релятивистский случай
Предположим, что речь идет о невзаимодействующих материальных точках, имеющих скорости порядка 10 в 8-й степени или чуть меньше в системе СИ. Трехмерный импульс рассчитывается по формуле 7, где под с понимают скорость света вакууме.
В случае, когда она замкнутая, верен закон сохранения количества движения. В то же время трехмерный импульс не является релятивистски инвариантной величиной, так как присутствует его зависимость от системы отсчета. Есть также четырехмерный вариант. Для одной материальной точки его определяют по формуле 8.
Импульс и энергия
Эти величины, а также масса тесно связаны друг с другом. В практических задачах обычно применяются соотношения (9) и (10).
Определение через волны де Бройля
В 1924 году была высказана гипотеза о том, что корпускулярно-волновым дуализмом обладают не только фотоны, но и любые другие частицы (протоны, электроны, атомы). Ее автором стал французский ученый Луи де Бройль. Если перевести эту гипотезу на язык математики, то можно утверждать, что с любой частицей, имеющей энергию и импульс, связана волна с частотой и длиной, выражаемыми формулами 11 и 12 соответственно (h — постоянная Планка).
Из последнего соотношения получаем, что модуль импульса и длина волны, обозначаемая буквой «лямбда», обратно пропорциональны друг другу (13).
Если рассматривается частица со сравнительно невысокой энергией, которая движется со скоростью, несоизмеримой со скоростью света, то модуль импульса вычисляется так же, как в классической механике (см. формулу 1). Следовательно, длина волны рассчитывается согласно выражению 14. Иными словами, она обратно пропорциональна произведению массы и скорости частицы, т. е. ее импульсу.

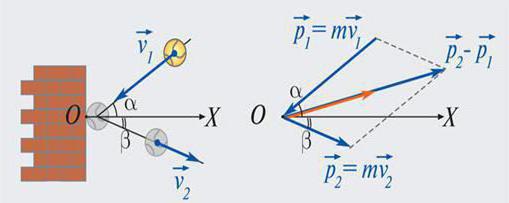
Теперь вы знаете, что импульс тела — это мера механического движения, и познакомились с его свойствами. Среди них в практическом плане особенно важен Закон сохранения. Даже люди, далекие от физики, наблюдают его в повседневной жизни. Например, всем известно, что огнестрельное оружие и артиллерийские орудия дают отдачу при стрельбе. Закон сохранения импульса наглядно демонстрирует и игра в бильярд. С его помощью можно предсказать направления разлета шаров после удара.
Закон нашел применение при расчетах, необходимых для изучения последствий возможных взрывов, в области создания реактивных аппаратов, при проектировании огнестрельного оружия и во многих других сферах жизни.
И́мпульс (коли́чество движе́ния) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы этого тела на его скорость , направление импульса совпадает с направлением вектора скорости:
В более общем виде, справедливом также и в релятивистской механике, определение имеет вид:
Импульс — это аддитивный интеграл движения механической системы, связанный согласно теореме Нётер с фундаментальной симметрией — однородностью пространства.
История появления термина[править | править код]
Средневековые натурфилософы, в соответствии с учением Аристотеля, полагали, что для поддержания движения непременно требуется некоторая сила, без силы движение прекращается. Часть учёных выдвинула возражение против этого утверждения: почему брошенный камень продолжает двигаться, хотя связь с силой руки утрачена?
Для ответа на подобные вопросы Жан Буридан (XIV век) изменил ранее известное в философии понятие «импетус». По Буридану, летящий камень обладает «импетусом», который сохранялся бы в отсутствие сопротивления воздуха. При этом «импетус» прямо пропорционален скорости. В другом месте он пишет о том, что тела с бо́льшим весом способны вместить больше импетуса.
В первой половине XVII века Рене Декартом было введено понятие «количества движения». Он высказал предположение о том, что сохраняется не только количество движения одного тела, изолированного от внешних воздействий, но и любой системы тел, взаимодействующих лишь друг с другом. Физическое понятие массы в то время ещё не было формализовано — и он определил количество движения как произведение «величины тела на скорость его движения». Под скоростью Декарт подразумевал абсолютную величину (модуль) скорости, не учитывая её направление. Поэтому теория Декарта согласовывалась с опытом лишь в некоторых случаях (например, Валлис, Рен и Гюйгенс в 1668 году использовали её для исследования абсолютно упругого столкновения в системе центра масс).
Валлис в 1668 году первым предложил считать количество движения не скалярной, а направленной величиной, учитывая направления с помощью знаков «плюс» и минус»[1]. В 1670 году он окончательно сформулировал закон сохранения количества движения. Экспериментальным доказательством закона послужило то, что новый закон позволял рассчитывать неупругие удары, а также удары в любых системах отсчёта.
Закон сохранения количества движения был теоретически доказан Исааком Ньютоном через третий и второй закон Ньютона. Согласно Ньютону, «количество движения есть мера такового, устанавливаемая пропорционально скорости и массе».
Определение импульса[править | править код]
Классическая механика[править | править код]
В классической механике полным импульсом системы материальных точек называется векторная величина, равная сумме произведений масс материальных точек на их скорости:
соответственно величина называется импульсом одной материальной точки. Это векторная величина, направленная в ту же сторону, что и скорость частицы. Единицей измерения импульса в Международной системе единиц (СИ) является килограмм-метр в секунду (кг·м/с).
Если мы имеем дело с телом конечного размера, не состоящим из дискретных материальных точек, для определения его импульса необходимо разбить тело на малые части, которые можно считать материальными точками, и просуммировать по ним, в результате получим:
Импульс системы, на которую не действуют никакие внешние силы (или они скомпенсированы), сохраняется во времени:
(*)
Сохранение импульса в этом случае следует из второго и третьего закона Ньютона: написав второй закон Ньютона для каждой из составляющих систему материальных точек и просуммировав по всем материальным точкам, составляющим систему, в силу третьего закона Ньютона получим равенство (*).
Релятивистская механика[править | править код]
В релятивистской механике трёхмерным импульсом системы невзаимодействующих материальных точек называется величина
где — масса -й материальной точки, — её скорость.
Для замкнутой системы не взаимодействующих материальных точек эта величина сохраняется. Однако трёхмерный импульс не есть релятивистски инвариантная величина, так как он зависит от системы отсчёта.
Более осмысленной величиной будет четырёхмерный импульс, который для одной материальной точки определяется как
На практике часто применяются следующие соотношения между массой, импульсом и энергией частицы:
В принципе, для системы невзаимодействующих материальных точек их 4-импульсы суммируются. Однако для взаимодействующих частиц в релятивистской механике следует учитывать импульсы не только составляющих систему частиц, но и импульс поля взаимодействия между ними. Поэтому гораздо более осмысленной величиной в релятивистской механике является тензор энергии-импульса, который в полной мере удовлетворяет законам сохранения.
Свойства импульса[править | править код]
- Аддитивность. Это свойство означает, что импульс механической системы, состоящей из материальных точек, равен сумме импульсов всех материальных точек, входящих в систему.[2]
- Инвариантность по отношению к повороту системы отсчета. [2]
- Сохранение. Импульс не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы. Это свойство инвариантно по отношению к преобразованиям Галилея[2]. Свойства сохранения кинетической энергии, сохранения импульса и второго закона Ньютона достаточно, чтобы вывести математическую формулу импульса.[3][4]
Обобщённый импульс в теоретической механике[править | править код]
В теоретической механике обобщённым импульсом называется частная производная лагранжиана системы по обобщённой скорости
В случае, если лагранжиан системы не зависит от некоторой обобщённой координаты, то в силу уравнений Лагранжа
Для свободной частицы в релятивистской механике функция Лагранжа имеет вид: , отсюда:
Независимость лагранжиана замкнутой системы от её положения в пространстве следует из свойства однородности пространства: для хорошо изолированной системы её поведение не зависит от того, в какое место пространства мы её поместим. По теореме Нётер из этой однородности следует сохранение некоторой физической величины. Эту величину и называют импульсом (обычным, не обобщённым).
Обобщённый импульс в электромагнитном поле[править | править код]
В электромагнитном поле обобщённый импульс частицы равен:
где — векторный потенциал электромагнитного поля.
Формальное определение импульса[править | править код]
Импульсом называется сохраняющаяся физическая величина, связанная с однородностью пространства (инвариант относительно трансляций).
Импульс электромагнитного поля[править | править код]
Электромагнитное поле, как и любой другой материальный объект, обладает импульсом, который легко можно найти, проинтегрировав вектор Пойнтинга по объёму:
(в системе СИ).
Существованием импульса у электромагнитного поля объясняется, например, такое явление, как давление электромагнитного излучения.
Импульс в квантовой механике[править | править код]
Формальное определение[править | править код]
В квантовой механике оператором импульса частицы называют оператор — генератор группы трансляций. Это эрмитов оператор, собственные значения которого отождествляются с импульсом системы частиц. В координатном представлении для системы нерелятивистских частиц он имеет вид
где — оператор набла, соответствующий дифференцированию по координатам -ой частицы. Гамильтониан системы выражается через оператор импульса:
Для замкнутой системы () оператор импульса коммутирует с гамильтонианом и импульс сохраняется.
Определение через волны де Бройля[править | править код]
Формула де Бройля связывает импульс и длину волны де Бройля.
Модуль импульса обратно пропорционален длине волны :
где — постоянная Планка.
Для частиц не очень высокой энергии, движущихся со скоростью (скорости света), модуль импульса равен (где — масса частицы), и
Следовательно, длина волны де Бройля тем меньше, чем больше модуль импульса.
В векторном виде это записывается как:
где — волновой вектор.
Импульс в гидродинамике[править | править код]
В гидродинамике вместо массы материальной точки рассматривают массу единицы объёма, то есть плотность жидкости или газа . А вместо импульса фигурирует вектор плотности импульса, совпадающий по смыслу с вектором плотности потока массы
Поскольку в турбулентном потоке характеристики состояния вещества (в том числе, плотность и скорость) подвержены хаотическим пульсациям, физический интерес представляют осреднённые величины. Влияние гидродинамических флуктуаций на динамику потока учитывается методами статистической гидромеханики, в которой уравнения движения, описывающие поведение средних характеристик потока, в соответствии с методом О. Рейнольдса, получаются путём осреднения уравнений Навье-Стокса[5]. Если, в согласии с методом Рейнольдса, представить , , где черта сверху — знак осреднения, а штрих — отклонения от среднего, то вектор осреднённой плотности импульса приобретёт вид:
где — вектор плотности флуктуационного потока массы (или «плотность турбулентного импульса»[5]).
Импульсное представление в квантовой теории поля[править | править код]
В квантовой теории поля часто употребляется импульсное представление на основе использования преобразования Фурье. Его преимуществами являются: удобство описания физических систем при помощи энергий и импульсов, а не при помощи пространственно-временных координат; более компактная и наглядная структура динамических переменных.[6]
См. также[править | править код]
- Импульс силы
- Момент импульса
- Закон сохранения импульса
- Электрический импульс
Литература[править | править код]
- Арнольд В. И. Математические методы классической механики. — 5-е изд., стереотипное. — М.: Едиториал УРСС, 2003. — 416 с. — 1500 экз. — ISBN 5-354-00341-5.
- Ландау Л. Д., Лифшиц Е. М. Механика. — Издание 4-е, исправленное. — М.: Наука, 1988. — 215 с. — («Теоретическая физика», том I). — ISBN 5-02-013850-9.
- Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7.
- Сивухин Д. В. Общий курс физики. — Издание 4-е. — М.: Физматлит, 2002. — Т. I. Механика. — 792 с. — ISBN 5-9221-0225-7.
- Айзерман М. А. Классическая механика. — М.: Наука, 1980. — 368 с.
Примечания[править | править код]
- ↑ Григорьян А. Т. Механика от античности до наших дней. — М.: Наука, 1974.
- ↑ 1 2 3 Айзерман, 1980, с. 49.
- ↑ Айзерман, 1980, с. 54.
- ↑ Сорокин В. С. «Закон сохранения движения и мера движения в физике» // УФН, 59, с. 325–362, (1956)
- ↑ 1 2 Монин А. С., Яглом А. М. Статистическая гидромеханика. Часть 1. — М.: Наука, 1965. — 639 с.
- ↑ Боголюбов Н. Н., Ширков Д. В. Квантовые поля. — М., Наука, 1980. — с. 25
Изучив законы Ньютона, мы видим, что с их помощью можно решить основные задачи механики, если нам известны все силы, действующие на тело. Есть ситуации, в которых определить эти величины затруднительно или вообще невозможно. Рассмотрим несколько таких ситуаций. При столкновении двух биллиардных шаров или автомобилей мы можем утверждать о действующих силах, что это их природа, здесь действуют силы упругости. Однако ни их модулей, ни их направлений мы точно установить не сможем, тем более что эти силы имеют крайне малое время действия. При движении ракет и реактивных самолетов мы также мало что можем сказать о силах, приводящих указанные тела в движение. В таких случаях применяются методы, позволяющие уйти от решения уравнений движения, а сразу воспользоваться следствиями этих уравнений. При этом вводятся новые физические величины. Рассмотрим одну из этих величин, называемую импульсом тела
Импульс силы. Импульс тела
Понятие импульса было введено еще в первой половине XVII века Рене Декартом, а затем уточнено Исааком Ньютоном. Согласно Ньютону, который называл импульс количеством движения, – это есть мера такового, пропорциональная скорости тела и его массе. Современное определение: импульс тела – это физическая величина, равная произведению массы тела на его скорость:
= m
Прежде всего, из приведенной формулы видно, что импульс – величина векторная и его направление совпадает с направлением скорости тела, единицей измерения импульса служит:
[ ] = [ кг· м/с]
Рассмотрим, каким же образом эта физическая величина связана с законами движения. Запишем второй закон Ньютона, учитывая, что ускорение есть изменение скорости с течением времени:
Налицо связь между действующей на тело силой, точнее, равнодействующей сил и изменением его импульса. Величина произведения силы на промежуток времени носит название импульса силы. Из приведенной формулы видно, что изменение импульса тела равно импульсу силы.
Какие эффекты можно описать с помощью данного уравнения (рис. 1)?
Рис. 1. Связь импульса силы с импульсом тела (Источник)
Стрела, выпускаемая из лука. Чем дольше продолжается контакт тетивы со стрелой (∆t), тем больше изменение импульса стрелы (∆ ), а следовательно, тем выше ее конечная скорость.
Два сталкивающихся шарика. Пока шарики находятся в контакте, они действуют друг на друга с равными по модулю силами, как учит нас третий закон Ньютона. Значит, изменения их импульсов также должны быть равны по модулю, даже если массы шариков не равны.
Проанализировав формулы, можно сделать два важных вывода:
1. Одинаковые силы, действующие в течение одинакового промежутка времени, вызывают одинаковые изменения импульса у различных тел, независимо от массы последних.
2. Одного и того же изменения импульса тела можно добиться, либо действуя небольшой силой в течение длительного промежутка времени, либо действуя кратковременно большой силой на то же самое тело.
Согласно второму закону Ньютона, можем записать:
∆t = ∆ = ∆ / ∆t
Отношение изменения импульса тела к промежутку времени, в течение которого это изменение произошло, равно сумме сил, действующих на тело.
Проанализировав это уравнение, мы видим, что второй закон Ньютона позволяет расширить класс решаемых задач и включить задачи, в которых масса тел изменяется с течением времени.
Если же попытаться решить задачи с переменной массой тел при помощи обычной формулировки второго закона Ньютона:
= m,
то попытка такого решения привела бы к ошибке.
Примером тому могут служить уже упоминаемые реактивный самолет или космическая ракета, которые при движении сжигают топливо, и продукты этого сжигаемого выбрасывают в окружающее пространство. Естественно, масса самолета или ракеты уменьшается по мере расхода топлива.
Краткие итоги
Несмотря на то что второй закон Ньютона в виде «равнодействующая сила равна произведению массы тела на его ускорение» позволяет решить довольно широкий класс задач, существуют случаи движения тел, которые не могут быть полностью описаны этим уравнением. В таких случаях необходимо применять другую формулировку второго закона, связывающую изменение импульса тела с импульсом равнодействующей силы. Кроме того, существует ряд задач, в которых решение уравнений движения является математически крайне затруднительным либо вообще невозможным. В таких случаях нам полезно использовать понятие импульса.
Вывод второго закона Ньютона
С помощью закона сохранения импульса и взаимосвязи импульса силы и импульса тела мы можем вывести второй и третий закон Ньютона.
Второй закон Ньютона выводится из соотношения импульса силы и импульса тела.
Импульс силы равен изменению импульса тела:
Произведя соответствующие переносы, мы получим зависимость силы от ускорения, ведь ускорение определяется как отношение изменения скорости ко времени, в течение которого это изменение произошло:
Подставив значения в нашу формулу, получим формулу второго закона Ньютона:
Вывод третьего закона Ньютона
Для выведения третьего закона Ньютона нам понадобится закон сохранения импульса.
Векторы подчеркивают векторность скорости, то есть то, что скорость может изменяться по направлению. После преобразований получим:
Так как промежуток времени в замкнутой системе был величиной постоянной для обоих тел, мы можем записать:
Мы получили третий закон Ньютона: два тела взаимодействуют друг с другом с силами, равными по величине и противоположными по направлению. Векторы этих сил направлены навстречу друг к другу, соответственно, модули этих сил равны по своему значению.
Список литературы
- Тихомирова С.А., Яворский Б.М. Физика (базовый уровень) – М.: Мнемозина, 2012.
- Генденштейн Л.Э., Дик Ю.И. Физика 10 класс. – М.: Мнемозина, 2014.
- Кикоин И.К., Кикоин А.К. Физика – 9, Москва, Просвещение, 1990.
Домашнее задание
- Дать определение импульсу тела, импульсу силы.
- Как связаны импульс тела с импульсом силы?
- Какие выводы можно сделать по формулам импульса тела и импульса силы?
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Questions-physics.ru (Источник).
- Интернет-портал Frutmrut.ru (Источник).
- Интернет-портал Fizmat.by (Источник).
